基于近邻的不均衡数据聚类算法
2020-10-12汪玉枝高晓楠
武 森,汪玉枝,高晓楠
北京科技大学经济管理学院,北京 100083✉通信作者,E-mail: gaoxiaonan0001@163.com
聚类分析是数据挖掘领域最为常见的技术之一,用于发现数据集中未知的对象类[1]. 聚类分析在客户细分[2]、模式识别[3]、医疗决策[4]、异常检测[5]等诸多领域有着广泛的应用前景. 传统的聚类算法能够很好地处理均衡数据的聚类问题,但是现实生活中存在许多不均衡数据,例如医疗诊断[6]、故障诊断[7]等领域的数据中表现正常的数据量要远远大于表现异常的数据量. 这类不均衡数据集的特点是同一数据集中归属于某一类别的数据对象的数量和密度与其他类别数据对象的数量和密度有较大差异,通常数据对象数量较多的类称之为大类,数据对象数量较少的类称之为小类. 对于不均衡数据的聚类问题,传统的聚类算法处理能力较弱. 以著名的 K–means算法为例,K–means算法是经典的划分式聚类算法,在处理不均衡数据集时,容易出现“均匀效应”[8],即聚类时往往会产生相对均匀尺寸的类,小类中的数据对象会“吞掉”大类中的部分数据对象,造成聚类结果中不同类的数据对象数量和密度趋于一致.
为解决不均衡数据的聚类问题,研究者从不同角度提出了多种方法,大致可以分成以下三类:(1)数据预处理[9−12];(2)多中心点[13−14];(3)优化目标函数[15−16]. 第一类方法是数据预处理,此类方法对数据集进行欠采样和过采样处理后再进行聚类,但是欠采样方法仅仅采用了属于大类中的一部分具有代表性的子集,导致大类中大量的有效信息被忽略,影响了聚类效果[17];过采样方法通过增加小类中对象数量来进行数据分析,使原有数据集达到均衡状态,但是这样做一方面可能导致过拟合,另一方面也可能给数据集带来噪声. 第二类方法是多中心点的方法,此类方法基于多中心的角度解决K–means的“均匀效应”问题,其思想是用多个类中心代替单个类中心代表一个类,在某些情况下,借助该思想,K–means算法在迭代过程中根据距离“中心”最近的原则,能够让部分被错分到小类中的数据对象校正回大类中. 如亓慧提出了一种多中心的不均衡K_均值聚类方法(MC_IK)[14],具有一定的有效性和可行性. 但此类方法对于一些大类分布极其不均匀的不均衡数据聚类问题,不能全面地反映数据分布特征,导致算法的有效性降低. 第三类方法是优化目标函数的方法,此类方法从目标函数优化的角度提出新的算法,通过推导出相应的聚类优化目标函数,以解决“均匀效应”问题. 如杨天鹏通过优化数据离散程度进而优化目标函数,提出了一种基于变异系数的聚类算法(CVCN)[15]. 这类方法从目标函数直接切入,相比于之前的聚类算法是一种较为直接的新方法且有一定的实用性,但是此类方法一般涉及目标函数参数的求解,属于非线性函数优化问题,难以得到全局最优解,这决定了该类算法的聚类结果具有相对较大的随机性,影响算法的聚类精度.
针对上述问题,本文借助近邻思想,提出基于近邻的不均衡数据聚类算法(CABON). 首先运用K–means算法对数据对象进行初始聚类,针对聚类结果中部分数据对象类别可能划分错误的问题,从数据对象与其最近的两个类中心距离差值的计算出发,给出了类别待定集的定义及构造规则,用以确定初始聚类结果中类别归属有待进一步核定的数据对象集合. 其次针对类别待定集中数据对象所属类别的重新划分问题,提出了一种新的类的划分规则,通过查找类别待定集中每个数据对象的最近邻居,借助近邻思想,将类别待定集的数据对象按照从集合边缘到中心的顺序依次归入其最近邻居所在的类别中,能够将初次聚类结果中类别错分的数据对象校正回正确的类,并且定义了一种类别待定集的动态调整机制,提高数据对象类别划分的准确率,从而进一步消减K–means算法的“均匀效应”,得到最终的聚类结果.
1 相关概念与规则
1.1 K–means算法的“均匀效应”
K–means算法是划分式聚类的经典算法,在K–means算法迭代过程中,采用一个类中所有对象的平均值作为该类新的中心,然后根据距离“中心”最近原则,重新确定所有对象的类别,这会导致K–means算法在处理不均衡数据集时,出现部分数据对象与多个类中心距离相近的情况,从而导致这部分的数据对象归属类别被错分. 文献[8]介绍了K–means算法的“均匀效应”,即K–means习惯于将大类中的部分对象划分到小类中,从而使获得的类拥有相对均匀的尺度. 如图1(a)所示,展示了一个由Python人工合成的二维不均衡数据集的真实分布,两个类的数据对象的数量和密度有较大差别;图 1(b)为 K–means算法对图 1(a)中数据集的聚类结果,可以看到,聚类后小类“吞掉”了大类中的部分数据对象,使得两个类的数据对象的数量和密度趋于相近,此为K–means算法所产生的“均匀效应”现象. 从类中心的角度来说,因为单个类中心不能充分反映一个大类的特征,导致大类中的部分数据对象被划分到小类中[18]. 在K–means算法迭代过程中,当大类中心与小类中心的距离越来越近,大类中的部分对象极易被错分到小类中,最终的聚类结果产生的“均匀效应”就越显著.

图1 二维不均衡数据集的真实分布和 K–means的聚类结果. (a)数据集真实分布;(b) K–means的聚类结果Fig.1 Real distributions of two-dimensional unbalanced data sets and clustering results of the K–means algorithm: (a) real distribution of datasets; (b) the clustering result of the K–means algorithm

图2 MC_IK算法中模糊工作集构造规则存在缺陷示意图. (a)数据集真实分布;(b)MC_IK对数据集初次聚类结果Fig.2 Schematic diagram of the defects in the construction rules of the MC_IK algorithm’s fuzzy working set: (a) real distribution of data sets; (b) initial clustering result of the MC_IK algorithm on datasets
1.2 类别待定集
类别待定集是数据集中所属类别有待进一步核定的数据对象构成的集合,对应地,数据集中所属类别确定的数据对象构成的集合称之为类别确定集. 在CABON算法中,首先运用K–means对数据对象进行聚类,得到初始聚类结果. 由于传统的K–means算法不能很好地处理不均衡数据的聚类问题,因此在初始聚类结果中会造成部分数据对象在算法迭代过程中与多个类中心距离都较为相近,以至于无法准确确定其类别,出现类别错分的情况.基于此,本文定义了一种构造规则来确定类别待定集,并进一步提出一种新的类的划分规则实现对类别待定集中数据对象的重新划分,得到最终聚类结果,从而处理不均衡数据的“均匀效应”问题.
已有研究MC_IK算法提出过一种模糊工作集的定义:对于任意一个数据对象,若与初次聚类结果中任意两类或两类以上的类中心距离差小于预设阈值,则将此数据对象归入模糊工作集[14]. 但是,这种构造方法可能将普通数据对象划归到模糊工作集中,存在模糊工作集构造不精准的缺点,影响算法的聚类效果. 如图2(a)所示,三角形、圆圈、正方形和四角星分别代表了四种类别,其类中心分别是c1、c2、c3、c4,图 2(b)是图 2(a)中数据集的初次聚类结果,可以看到,Cluster 1和Cluster 2之间发生了“均匀效应”. 对于对象x1,根据MC_IK算法定义的模糊工作集的构造规则,其与初次聚类结果中类中心c3、c4的距离差值最小,若此距离差值小于预设阈值可将数据对象x1归入模糊工作集. 但实际上对象x1与初次聚类结果中最近的两个类中心为c1、c2,且距离c1、c2的距离差值较大,这种情况下可以把对象x1直接归入距离最近的类别c2中,不属于模糊工作集. 因此,MC_IK算法定义的构造规则会导致部分对象被误分到模糊工作集,影响算法的聚类效果.
因此,在MC_IK算法定义的模糊工作集的基础上,本文将数据集中所属类别有待进一步核定的数据对象构成的集合定义为类别待定集,构造规则为:使用K–means算法对数据对象进行聚类得到初始聚类结果后,对于任意一个数据对象,若与初始聚类结果中最近的两个类中心距离差小于预设阈值δ(即类别待定集构造阈值),则将此数据对象归入类别待定集. 图 3(a)为用 K–means算法对原始数据对象聚类得到的初始聚类结果,产生了“均匀效应”;图3(b)根据本文定义的构造规则确定了类别待定集,虚线内数据对象距离最近的两个类中心距离差小于预设阈值δ,构成了类别待定集. 相比于MC_IK算法中定义的模糊工作集,本文提出的类别待定集构造方法可以有效避免归属类别确定的数据对象被错分到类别模糊不确定的集合里的情形,能够准确识别可能被错分的数据对象,为后续数据对象的重新划分打好基础.

图3 类别待定集的构造过程示意图. (a)K–means算法对数据集的初始聚类结果;(b)CABON 算法构造类别待定集图示Fig.3 Schematic of the construction process of the undetermined-cluster set: (a) initial clustering result of the K-means algorithm on data sets; (b)undetermined-cluster set constructed by the CABON algorithm
1.3 类别待定集中数据对象的划分规则
初始类别待定集构造完成后,为了将该集合中数据对象准确地划分到正确的类中,CABON算法定义了一种新的类的划分规则. 规则描述如下:(1)查找类别待定集中每个数据对象在类别确定集中的最近邻居,这些最近邻居数据对象构成一个集合,称之为最近邻居集;(2)依据距离最近邻居距离最小原则,确定类别待定集的边界对象,并将边界对象归入其最近邻居所在类别中;(3)将已经重新划分过类别的边界对象从类别待定集中删除,并添加到类别确定集中,动态调整类别待定集;(4)重复第(2)、(3)步,直到类别待定集为空.
在上述规则中可以看出,CABON算法在实现过程中,类别待定集中的对象不是固定不变的,因为类别待定集固定的思路仍会导致数据对象类别错分的情况,利用上述规则中类别待定集的动态调整机制可以避免这一情况的发生. 如图4所示,三角形和圆圈分别代表初始聚类得到的两种类别,虚线内对象代表已构造好的类别待定集. 按照上述类别待定集中数据对象的划分规则,随着类别待定集的动态调整,对象x1应归入大类Cluster1中. 若类别待定集是固定的,即虚线内对象在算法的迭代过程中不发生变化,CABON算法在计算类别待定集中数据对象与类别确定集中数据对象之间的距离时,对象x1与对象x3的距离略大于对象x1与 对 象x2的 距 离 (d(x1,x3)>d(x1,x2)), 且d(x1,x2)为距离集合里的最小值,因此对象x1的最近邻居为小类中的对象x2,其类别也将与对象x2一致.如此一来,类别待定集中原本应归入大类中的对象会被错分到小类中. 故在此基础上,我们定义类别待定集和类别确定集是动态变化的:当类别待定集中的边界对象类别确定后,将此边界对象从类别待定集中剔除并添加至类别确定集中,此对象的类别确定后就有可能成为类别待定集其他数据对象的最近邻居. 将类别待定集的每一数据对象按照从集合边缘到中心的顺序依次归入其最近邻居所在的类别中,实现类别待定集动态调整的过程,以避免上述类别待定集固定所导致的数据对象类别错分的后果.

图4 CABON 算法固定类别待定集的情况示意图Fig.4 Schematic of the CABON algorithm’s fixed of the undeterminedcluster set
图5展示了类别待定集中数据对象根据CABON算法所定义的类划分规则实现类划分的过程. 首先,图5(a)在图3(b)构造的类别待定集的基础上,确定了类别待定集中每一个数据对象在类别确定集中的最近邻居;其次,根据二者距离的大小选择距离最小的数据对象作为边界对象,即图5(a)中虚线内有颜色填充的对象为此次迭代中的边界对象,而虚线外有相同颜色填充的对象为边界对象对应的最近邻居;最后,根据近邻思想将边界对象归入其最近邻居所在的类中,由此确定边界对象的类别,进而将边界对象由类别待定集划分到类别确定集中(图 5(b)). 图 5 展示了类别待定集中数据对象类别重新划分的一次迭代过程,经过多次迭代后,类别待定集中的数据对象为空,表示所有数据对象已实现了类别的重新划分,得到了最后的聚类结果.
2 CABON 算法过程
Step 1:对数据集X用经典的 K–means算法聚类,得到初始聚类结果;
Step 2:构造类别待定集. 对于任意一个数据对象(i=1,2,…,n),选择距离最近的两个类与(s,t=1,2,…,k,s≠k),且它们的类中心为和,若与数据对象的距离符合如下关系:

Step 3:查找最近邻居集. 根据类别待定集中数据对象与类别确定集中数据对象的距离大小,在类别确定集中选取距离最小的对象集合作为的最近邻居集对应类别待定集中数据对象在类别确定集中的最近邻居);
Step 4:确定边界对象. 查找到距离最近邻居最小的数据对象, 确定为类别待定集的边界对象,将此边界对象归入其最近邻居所 在的类别中;同时将边界对象从类别待定集中剔除并添加到类别确定集中;
Step 5:重复 Step 3 至 Step 4,直到类别待定集为空集、类别确定集为全集时停止.
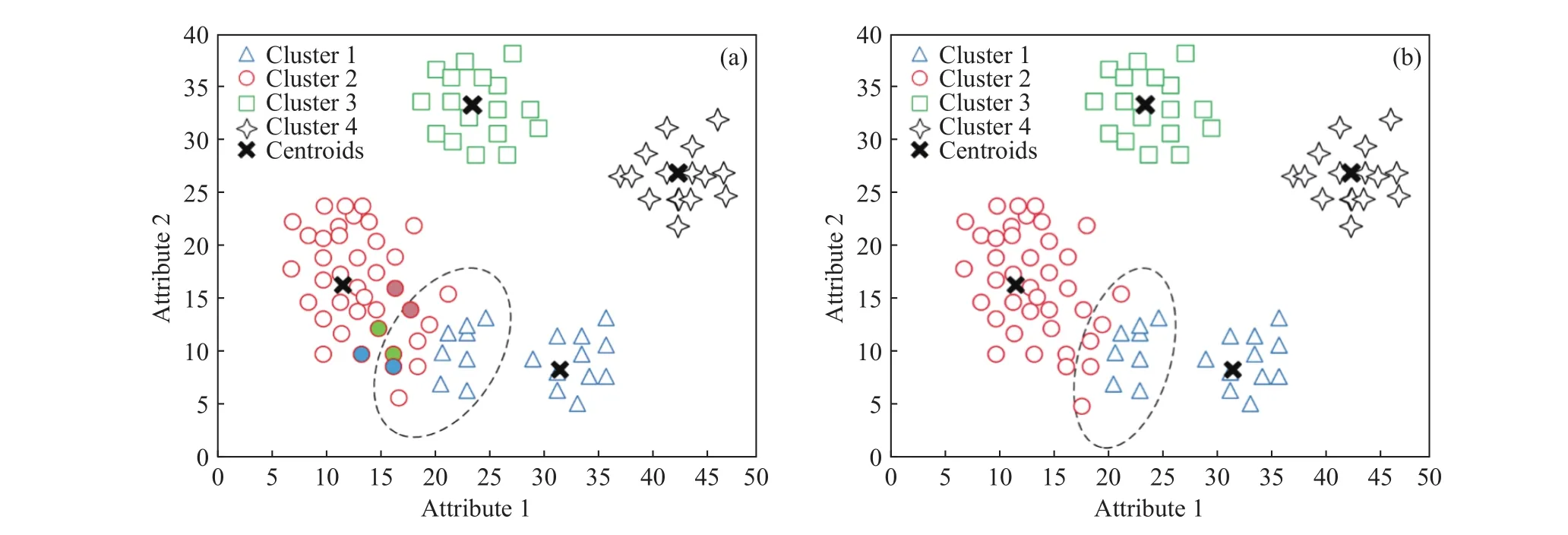
图5 类别待定集中数据对象类别重新划分过程示意图. (a)边界对象确定过程;(b)类别待定集调整过程Fig.5 Schematic of the reclassification process of data objects in the undetermined-cluster set: (a) determination of boundary objects; (b) the adjustment process of undetermined-cluster set
由CABON算法的具体实现步骤可知CABON算法具有两个显著特点:(1)从计算数据对象与其最近的两个类中心距离差的角度,提出了类别待定集的构造方法,弥补已有研究构造模糊工作集时部分对象被误分这一不足;(2)基于近邻思想,为类别待定集中对象重新定义一种新的类的划分规则. 利用类别待定集对象的最近邻居作为确定其类别的参照依据,可以更精确地划分类别待定集对象所归属的类别,并且CABON算法中类别待定集的动态调整机制大大降低了对象归属类别错分的概率,从而保证聚类结果的质量.
3 实验分析
3.1 实验数据
为了验证CABON算法解决K–means“均匀效应”问题的有效性,实验分别在6个人工数据集和4 个 UCI(University of California Irvine)真实数据集上进行,详细信息见表1,编号1~6为人工数据集具体信息,真实分布如图6所示,其中编号1~3描述的是测试聚类常用的Flame[19]、Aggregation[20]、Jain[21]数据集,编号4~6描述的是Python合成的3个数据集,分别为 DS1、DS2、DS3. 另外,表 1编号7~10为真实数据集的具体信息,实验采用了加州大学欧文分校提出的UCI标准数据库中的Wine[22]、 Newthyroid[23]、 Ionosphere[24]和 Heart[25]这4个数据集.
3.2 评价指标
为了评估CABON算法及对比算法的聚类效果,本文引入了4个评价指标,分别是聚类精度(Accuracy)[26]、F 值(F-measure)[8]、标准化互信息(Normalized mutual information, NMI)[15, 27, 28]和 兰德指数(Rand index,RI)[29−30],4 个评价指标的取值上界均为1,指标值越接近1,聚类效果越好.
设k为聚类个数,N为数据集中数据对象的个数,为数据集的实际类分布,为数据集的聚类结果为和的共同部分的基数,则聚类精度(Accuracy)的公式如(1)所示:

F-measure的计算公式如(2)所示:

其中:Recall和Precision分别表示数据集中真实聚类结果与聚类结果相比的召回率和准确率;β表示Recall和Precision的相对重要性,通常设为1.
NMI的计算公式如(3)所示:

其中:N为数据集的数据对象数量,为 属于类i的数据对象数量;为属于类的数据对象数量;为真实数据集中类i与聚类结果类相一致的数据对象数量;R、K分别对应真实数据集和聚类结果类中的类个数.
RI的计算公式如(4)所示:


表 1 数据集参数信息Table 1 Parameter information for the data set
其中:a表示被聚类结果和真实结果判定为同一类别的数据对的数目;b表示聚类结果和真实结果都将判定为不同类别的数据对的数目;h表示聚类结果认为同类,但真实结果认为不同类的数据对的数目;g表示聚类结果认为不同类,但真实结果认为同类的数据对的数目.

图6 人工数据集真实分布. (a) Flame;(b) Aggregation;(c) Jain;(d) DS1;(e) DS2;(f) DS3Fig.6 True distribution of synthetic data sets: (a) Flame; (b) Aggregation; (c) Jain; (d) DS1; (e) DS2; (f) DS3
3.3 实验设计
实验将CABON算法与K–means、MC_IK[14]和CVCN[15]算法进行对比. K–means算法是经典的聚类算法,作为对比算法可比较不同算法降低“均匀效应”影响的程度;MC_IK和CVCN算法分别从多中心和优化目标函数的角度有效降低了不均衡数据聚类中“均匀效应”问题的影响. 对比实验通过将CABON算法和这些算法进行对比,以衡量CABON算法处理不均衡数据聚类问题降低“均匀效应”影响的能力. 在设定实验参数方面,参数k是输入的聚类个数,可参考实验数据集类的数量设定.δ为构造类别待定集事先设定的参数,取值范围根据数据集的大小而确定. 在本实验中,若数据集较小,阈值δ的取值范围设定为0.5~1.5,以0.5为初始值、0.1为步长确定一个最优取值区间,表现为阈值δ在此区间内时聚类评价指标值最高;最优取值区间确定后,缩短步长为0.01,在此区间内选择一个最优值作为此数据集的类别待定集构造阈值,表现为阈值δ取到此参数值时聚类评价指标值最高. 同样地,若数据集较大,阈值δ的取值范围设定为1.0~2.0,以1.0为初始值、0.1为步长确定一个最优取值区间后,缩短步长为0.01,在此区间内再次选择一个最优值作为此数据集的类别待定集构造阈值.

表 2 人工数据集不同算法聚类结果(Accuracy 指标)Table 2 Clustering results of artificial data set with different algorithms (Accuracy indicators)
3.4 实验结果
(1)人工数据集实验结果.
表2~表5给出了CABON、K–means、MC_IK和CVCN算法对人工数据集的聚类结果. 从表2~表5中可以看出,CABON算法在大多数情况下明显优于其他三种算法,这在一定程度上说明CABON算法能够消减K–means算法产生的“均匀效应”.对于Flame、Aggregation数据集,CABON的各个指标值均优于对比算法,但是CABON在处理Jain数据集时的F-measure、NMI值略低于CVCN算法,其原因在于Jain为非球形不均衡数据集,CABON对部分此类数据集中的数据对象聚类时无法准确构建类别待定集,从而影响最后的聚类结果.
对于 3个合成的数据集(DS1、DS2、DS3),CABON算法的聚类精度均优于对比算法. DS1和DS2数据集在数据对象的数量和密度上有较大差异,CABON处理这两个数据集时取得了较好的聚类效果;对于DS3数据集,K–means算法对其聚类时在多个类之间产生了“均匀效应”,CABON算法的聚类精度、F-measure、RI指标值均接近于1,验证了该算法处理此类问题的有效性. 同时,CVCN算法在DS3数据集上的各个指标值均低于K–means算法,这在一定程度上说明CVCN算法在处理多类非均匀数据聚类问题上处理能力较弱. 另外,MC_IK 算法在DS1、DS2、DS3数据集上的实验表现较K–means而言有不同程度的提升,表明MC_IK算法对K–means在DS1、DS2、DS3上产生的“均匀效应”有消减作用.

表 3 人工数据集不同算法聚类结果(F-measure 指标)Table 3 Clustering results of artificial data set with different algorithms (F-measure indicators)

表 4 人工数据集不同算法聚类结果(NMI指标)Table 4 Clustering results of artificial data set with different algorithms (NMI indicators)

表 5 人工数据集不同算法聚类结果(RI指标)Table 5 Clustering results of artificial data set with different algorithms (RI indicators)

图7 Flame 数据集不同算法聚类结果图示. (a) CABON;(b) K–means;(c) MC_IK;(d) CVCNFig.7 Graphical representations of clustering results with different algorithms on Flame data sets: (a) CABON; (b) K–means; (c) MC_IK; (d) CVCN

图8 Aggregation 数据集不同算法聚类结果图示. (a) CABON;(b) K–means;(c) MC_IK;(d) CVCNFig.8 Graphical representations of clustering results with different algorithms on Aggregation data sets: (a) CABON; (b) K–means; (c) MC_IK; (d)CVCN
图7~图 12是 CABON、K–means、MC_IK和CVCN算法对人工数据聚类结果的图示,这与表2~表5中的数据基本吻合. 综上,人工数据集的实验结果表明CABON算法能够有效消减不均衡数据聚类的“均匀效应”.
(2)真实数据集实验结果.
表6~表9给出了CABON、K–means、MC_IK和CVCN算法分别对4个真实数据集进行聚类的结果,从表6~表9中可以看出,对于UCI上的4个真实数据集,CABON算法在大多数情况下明显优于其他三种算法. 对于Wine数据集而言,CABON算法的NMI值略低于MC_IK算法,但是其他三个指标值均高于对比算法;对于Newthyroid、Ionosphere数据集,CABON算法的各个指标值均优于对比算法;对于Heart数据集,CABON算法聚类精度和F-measure值略低于CVCN算法,但是NMI值和RI值均高于对比算法. 以上结果表明,CABON算法对于UCI中的真实不均衡数据集也能有效解决“均匀效应”问题,提高聚类效果.

图9 Jain 数据集不同算法聚类结果图示. (a) CABON;(b) K–means;(c) MC_IK;(d) CVCNFig.9 Graphical representations of clustering results with different algorithms on Jain data sets: (a) CABON; (b) K–means; (c) MC_IK; (d) CVCN

图10 DS1 数据集不同算法聚类结果图示. (a) CABON;(b) K–means;(c) MC_IK;(d) CVCNFig.10 Graphical representations of clustering results with different algorithms on DS1 data sets: (a) CABON; (b) K–means; (c) MC_IK; (d) CVCN

图11 DS2 数据集不同算法聚类结果图示. (a) CABON;(b) K–means;(c) MC_IK;(d) CVCNFig.11 Graphical representations of clustering results with different algorithms on DS2 data sets: (a) CABON; (b) K–means; (c) MC_IK; (d) CVCN

图12 DS3 数据集不同算法聚类结果图示. (a) CABON;(b) K–means;(c) MC_IK;(d) CVCNFig.12 Graphical representations of clustering results with different algorithms on DS3 data sets: (a) CABON; (b) K–means; (c) MC_IK; (d) CVCN

表 6 UCI数据集不同算法聚类结果(Accuracy 指标)Table 6 Clustering results of UCI dataset with different algorithms(Accuracy indicators)

表 7 UCI数据集不同算法聚类结果(F-measure 指标)Table 7 Clustering results of UCI dataset with different algorithms(F-measure indicators)

表 8 UCI数据集不同算法聚类结果(NMI指标)Table 8 Clustering results of UCI dataset with different algorithms(NMI indicators)

表 9 UCI数据集不同算法聚类结果(RI指标)Table 9 Clustering results of UCI dataset with different algorithms(RI indicators)
总体来说,本文提出的CABON算法明显优于其他三种对比算法. 人工数据集和真实数据集的实验结果,验证了CABON算法在解决不均衡数据聚类的“均匀效应”问题和提高聚类效果上的可行性和有效性.
4 结论
(1)针对 K–means算法的“均匀效应”问题,从计算数据对象与其最近的两个类中心距离差的角度,给出了类别待定集的定义,解决了已有研究构造模糊工作集时部分数据对象类别被错分这一问题,间接提高了算法的聚类质量.
(2)针对不均衡数据的聚类问题,提出了基于近邻的不均衡数据聚类算法(CABON). CABON算法在对给定的数据集进行初始聚类后,针对初始聚类结果按照预设阈值δ构造类别待定集,基于近邻思想将类别待定集中数据对象归入其最近邻居所在的类别中,并动态更新类别待定集,得到最终的聚类结果.
(3)人工数据集和UCI真实数据集的实验结果表明,CABON算法能够有效消减K–means算法所产生的“均匀效应”. 与K–means以及专门针对不均衡数据聚类的MC_IK和CVCN算法的实验对比表明,CABON算法的聚类精度有明显提升.
