一种基于多变量公钥密码体制的改进签名模型

王 鑫,韩志宇,王新梅,杨 帆

(1.陕西科技大学 电子信息与人工智能学院，陕西 西安 710021;2.西安电子科技大学 通信工程学院,陕西 西安 710126)

0 引言

后量子密码体制已经发展了大约30年.特别是近10年来签名领域发展迅猛,涌现出许多引人注目的研究成果，如同态哈希函数多变量签名方案[1]，以及扩展merkle签名方案(XMSS)[2]和G-Merkle[3,4]XMSS等.此外,寻找新一代的公钥密码体制以抵抗量子计算机的攻击,已经成为近年来一项重要的挑战.美国科学家Peter Shor于1995年提出了一种量子分解算法[5,6],它通过利用量子计算的并行性,可以在多项式时间内快速分解出大数的质因子和离散对数问题,对现有基于传统密码体制的数字签名的安全性构成了严重威胁.

后量子密码体制的研究方向主要基于如下四类：基于格理论的密码体制[7]、基于编码理论的密码体制[8]、基于Hash函数的密码体制[9]和多变量公钥密码体制.多变量公钥密码体制是有限域上根据多变量非线性方程组的求解问题而设计的密码体制,其安全性基于求解一组多变量多项式方程,是一个NP-C困难问题[10].类似的是对称密码体制中分组密码AES的S盒其本质即为有限域上一个高次多变量多项式方程组.多变量公钥密码体制目前被认作是量子时代的一种安全的密码体制备选方案.2019年1月30日,美国国家标准技术研究院(NIST)启动一项关于后量子公钥加密标准草案的全球征集活动.经过一年的草案收集和第一轮审核,从最初的69种算法中选择了26种算法,进入后量子密码的半决赛.在候选的9种签名算法中,有4种是基于多变量公钥密码体制[11-14].

MI (Matsumoto and Imai)方案[15]是多变量公钥密码体制的一个基础性突破，随后又有很多新方案被提出，大致可以分为四类：MI体系、HFE(Hidden Field Equation)体系、OV (Oil Vinegar)体系和TTM(Tame Transformation Method)体系.不幸的是，这些体系的大多数密码方案已被攻破，现存的方案普遍被认为不适合加密，只适用于签名如UOV (Unbalanced Oil Vinegar)签名方案[11]和Rainbow签名方案[12].后续学者也投入了更多精力在这两种签名方案上[16-18].

然而,目前现有的基于多变量公钥密码体制的研究绝大部分集中在中心映射的设计上,通常采用如图2所示的签名结构；该模型还存在以下问题：按照该模型设计的签名产生和验证算法,隐含着签名验证仅依赖于外部公钥,并不涉及产生该消息签名时所对应的内部流程信息.这就使得在对方案进行攻击分析时,常常以寻找公钥方程之间潜在的内部代数关系为攻击目标[19,20].

基于线性化分析思想的伪造签名攻击即为这样一种有效分析方法,方法通过寻求或重新构造公钥P的外部结构,将内部隐藏的变量关系显性表达,构造更多的独立方程,再通过矩阵秩攻击对新方程求解[21,22].由于多变量体制核函数的构造使得大多数现有的加密或签名方案容易遭受此类攻击[23-27].特别是多变量体制的密钥具有冗余特性,通过该攻击所得到的解统计意义为其合法私钥对应的等价私钥,并非签名者的合法私钥,详细分析见文[28,29],矩阵秩的攻击方法可见文献[15]等.

原有签名模型中的签名验证“仅涉及消息和签名”而“不涉及内部过程信息”的验证是导致方案被攻破的关键所在.因为多变量公钥密码体制的中心映射是多对一的映射,所以自然就存在一个像对应多个原像的现象.而截至目前,多变量密码方案的设计多集中于中心映射的不断改进和新结构的不断提出,从签名模型的角度分析抵抗基于线性化分析思想的伪造签名攻击还未给出过相关研究.本文主要对原有签名模型存在的这一问题进行深入分析,通过借助签名附加值,增强签名验证条件,使得签名不仅确保外部信息的一致性,还必须具有内部信息的一致性,并以MI方案[15]为例进行具体分析.

本模型改进算法为量子时代安全签名方案设计提供了有益补充,并且方案运算仅涉及有限域上的加、乘,具有较高的效率和安全性,特别适用于存储空间和运算时间受限的场合,如智能卡、无线传感网络和动态RFID标签,为量子计算机时代的信息安全和信任体系的建立提供了必要的基础技术支撑.

1 多变量公钥密码体制的原有签名模型

多变量公钥密码体制具有庞大的代数结构[30,31],其公钥由一组非线性多变量多项式方程组构成.公钥P可看作三个映射的合成：P=ToQoS，符号o表示映射的合成，其中

分别为Fn和Fm上随机选取的可逆仿射变换，它们共同"掩藏"中心映射Q的结构，是私钥的重要部分.这里用Aff-1(Fn,Fm)表示Fn到Fm上的所有仿射变换，Aff-1(Fn)和Aff-1(Fm) 分别为Aff-1(Fn,Fn)和Aff-1(Fm,Fm)的缩写.

中心映射Q，是由n个变量m个多项式的方程组：

Q(x1,…,xn)|→

(q1(x1,…,xn),…,qm(x1,…,xn))

Q的结构通常公开，亦可部分保密，构成中心映射的方程称为中心方程.

三元组(T,Q,S)为私钥，对应的公钥即：

P(x1,…,xn) =

ToQoS(x1,…,xn)=

(p1(x1,…,xn),…,pm(x1,…,xn))

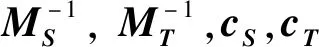
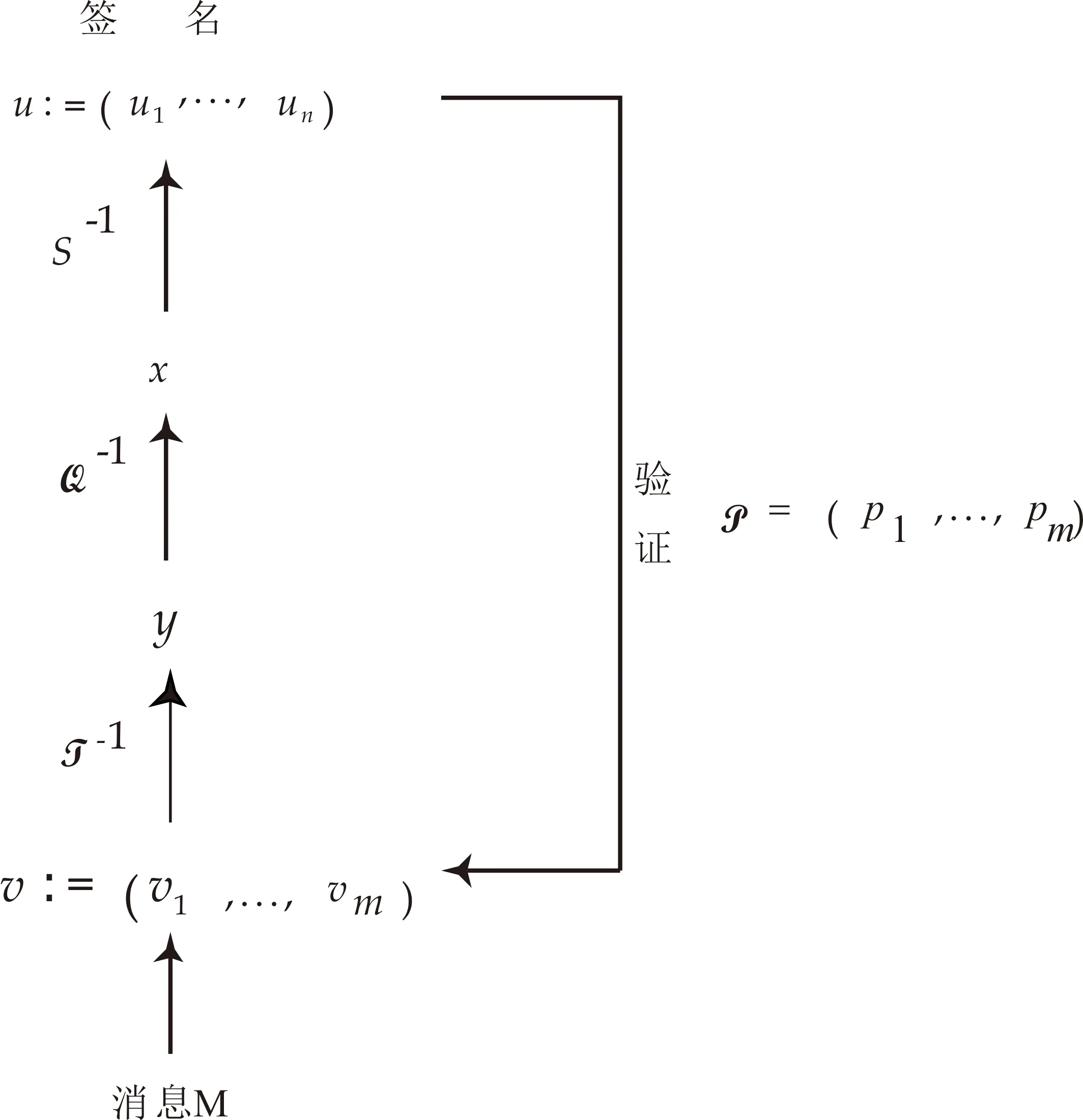
图1 多变量公钥密码系统的签名结构图

1.1 签名生成

已知一个消息M，取一个哈希函数H，使v=H(M)，依次计算y=T-1(v)，x=Q-1(y)和u=S-1(x).其中，S-1，T-1均为私钥S和T的可逆仿射变换.Q-1是中心映射Q的逆，求解Q-1时，需要结合Q的具体结构.

向量u=(u1,…,un)即是消息M的签名.

1.2 签名验证

由图1可知，签名验证即利用公玥P计算v=P(u)，若等式成立即为合法签名，否则签名无效.

1.3 MI方案

MI加密体制[15]通过使用基域及其扩域构造多变量公钥密码体制.

1.3.1 MI加密方案

设F是一q阶有限域，E是F的n次扩域，π:E→Fn是扩域到向量空间的同构映射，为

π(a0+a1x+…+an-1xn-1)=(a0,…,an-1)

Q(x1,…,xn)=

(q1(x1,…,xn),…,qn(x1,…,xn))=

其中，qi(x1,…,xn)i=1,…,m是n个变量的二次多项式方程.令S，T是Fn上的两个随机可逆仿射变换，则有公钥

P(x1,…,xn)=

(p1(x1,…,xn),…,pn(x1,…,xn))=

ToQoS(x1,…,xn)

其中，每一个多项式pn(n=1～n)均为二次.

1.3.2 MI签名方案

设消息为M，其编码值为(u1,…,um)，签名者的私钥为SSiger，TSiger,公钥为PSiger.签名者对消息M进行如下计算：

(1) 计算：

(2)计算：

(x1,…,xn)=Q-1(y1,…,ym)=

(3)计算：

则(v1,…,vn)即是消息(u1,…,vm)的签名.

1.4 线性化分析思想

多变量公钥密码体制的线性化分析思想是通过对已知的公钥方程或中心映射结构进行等价变形,将被隐藏的大量内部信息显性表达,通过产生更多的明密文方程,以期获得足够的线性无关方程,进而尝试消元求解.

然而,通过分析我们发现在多变量的签名产生和验证算法过程中,内部节点信息并未有效体现,也就是缺少和私钥相关联的内部信息流的有效验证.因此,对于多变量公钥密码体制的原有签名模型-签名有效判断仅通过公钥验证,借助对公钥的线性化分析势必会增加敌手成功的概率.

MI方案在高秩、低秩等直接分析中表现良好，却无法抵抗线性化分析的攻击求解等价私钥.对于公钥密码体制而言,若存在两个(甚至多个) 私钥和对应着同一公钥,那么我们就称这两个(多个) 私钥“等价”.多变量公钥密码体制的等价私钥是由于其本身庞大代数结构带来的,并且容易看出等价私钥的存在给签名的伪造提供了外部可能.基于线性化分析思想的攻击基本思路如下[32]：

设一组变量数为m的εm2个二次方程组，变量为x1,…,xm，其中ε为常数.通过变量代换变量为yij=xixj，原方程组变为变量数约有m2/2的εm2个线性方程组，其中i≤j.对于任何满足1≤a≤b≤c≤d≤m的四元组xaxbxcxd，存在三种不同的方式：

(xaxb)(xcxd)=(xaxc)(xbxd)=

(xaxd)(xbxc)⟹yabycd=

yacybd=yadybc

每互不相同的四元组都会产生2个方程，共存在大约m4/4!种不同的方程.进而，约产生m2/2个变量yij的m4/12 个二次方程，由于这些方程是线性独立，因此可再通过将每个变量yij替换为新变量zk的线性组合来表示，此时变量个数减少为(1/2-ε)m2个.进而，再对(1/2-ε)m2个关于变量zi的m4/12个二次方程继续用新变量vij替换每个乘积zizj(其中i≤j)做再次线性化.最终，得到具有m4/12个线性方程的新方程组，其中变量vij为((1/2-ε)m2)2/2个.

线性化过程中方程数与变量之间的关系如表1所示.

表1 线性化过程

借助于线性化分析方法，构造足够多的公钥方程，通过求解寻找合法私钥对应的等价私钥，进而可构造同一消息的一个有效签名，得以伪造签名成功.

2 改进签名模型描述

针对多变量密码体制签名模型的这一问题，通过重新设计公钥，增强签名生成和验证过程的严格性，提出一种可有效抵抗基于线性化分析思想攻击的改进模型.

2.1 参数生成

设有限域F，正整数n和m，F的n次扩域记为Fn，F的m次扩域记为Fm.取Fn到Fm上的一组多变量二次多项式方程q1(x1,…,xn),…,qm(x1,…,xn)为多变量公钥密码体制的中心映射，记为Q，其中输入变量为n，输出变量为m，Q-1即为多项式Q的逆多项式.另取Fn和Fm上可逆仿射变换S和T为私钥，其逆多项式分别记为S-1和T-1.随机选取Fn上的一组n个n元二次多项式方程组(g1(x1,…,xn),…,gn(x1,…,xn))，记为G，即G(x1,…,xn)=(g1(x1,…,xn),…,gn(x1,…,xn))，以及一个具有hash特性的单向不可逆的多项式方程组H.

用户私钥由S、T、G三部分构成，均为可逆仿射变换.H为可信第三方秘密选取，但仅用于公钥的产生，其中G的逆多项式表示为G-1.对应的公钥也由三个多项式构成，分别为P=ToQoS,HoG-1oS,HoS.

2.2 签名生成

已知消息M的编码为向量(u1,…,um) ，记做u，如图2所示，签名则按以下步骤产生：

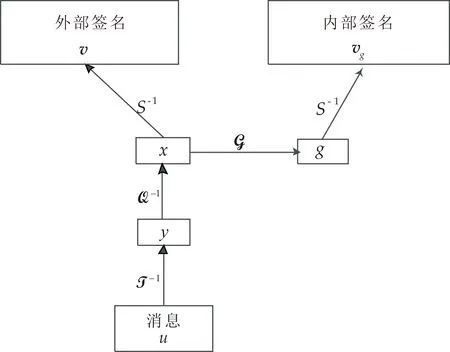
图2 改进模型中的签名生成

(S1)外部签名

已知消息M的编码值u=(u1,…,um)，依次由T-1，Q-1，S-1，计算得(v1,…,vn)，记为v，则v即为消息M的编码u的外部签名.

(S2)内部签名

对u=(u1,…,um)，经由T-1和Q-1计算结果为(x1,…,xn)，记为x.将x代入到G中，得G(x1,…,xn)=(g1(x1,…,xn),…,gn(x1,…,xn))=(g1,…,gn)记为g.

再将g代入到S-1中，得到S-1(g)oG(x)=(vg1,…,vgn)，记为vg.则vg即为消息M的编码u的内部签名.

将外部签名和内部签名级联得到v‖vg，即为消息M编码u的最终签名.

2.3 签名验证

改进模型中签名验证原理如图3所示.

图3 改进模型中签名验证

(V1)公钥P验证

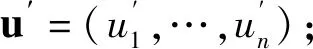
(V2)公钥HoS和HoG-1oS验证

将外部签名v=(v1,…,vn)代入到公钥HoS中，得

HoS(v)=HoS(v1,…,vn)=H(S(v1,…,vn))

记结果为h=(h1,…,hn)；将内部签名vg=(vg1,…,vgn)代入到公钥HoG-1oS中，得

HoG-1oS(vg)=HoG-1oS(vg1,…,vgn)=

H(G-1(S(vg1,…,vgn)))

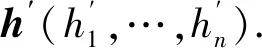
2.4 安全性分析

2.4.1 正确性

验证者收到按上述步骤产生的签名v‖vg，则有：

P(v)=P(S-1oQ-1oT-1(u1,…,um))=

PoS-1oQ-1oT-1(u)=

ToQoSoS-1oQ-1oT-1(u)=u

以及：

S(v)=(x1,…,xn)=G-1oS(vg)

HoS(v)=HoG-1oS(vg)

由上述可知其正确性成立.

2.4.2 安全性

相对于原有签名模型，改进模型实现了签名产生过程中内部信息流予以外部校验，有效签名必须结合内部节点信息的验证，而不仅仅依赖于外部公钥的唯一验证.实现每一签名的产生与合法私钥实现一致性绑定，有效阻止包括线性化分析思想在内的伪造签名攻击.

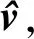
此外，随机秘密仿射变换的选取不泄露中心映射的结构信息，不影响签名的原有验证.使得改进模型具有一般通用性，保持原有方案核映射结构不变.因此，多变量公钥密码体制的其它类型的安全性分析，如高/低秩、差分分析等，均不受改进模型影响，安全级别保持不变.方案在不同参数下的具体体现可见文献[29].事实上，改进签名模型揭示了能通过公钥验证的签名并非一定是合法的，合法签名必须确保内部节点信息的一致性的事实.因此，增强内部节点信息准确一致性的验证，是提高签名有效性的一种有效方法.

3 MI在原有模型和改进模型中性能对比

3.1 改进模型MI签名方案

原签名模型只利用公钥验证P(v)=u，而改进模型，签名由两部分v和vg构成，除原有公钥验证P(v)=u，还利用公钥HoS和HoG-1oS验证内部节点的一致性：

HoS(v)=HoG-1oS(vg).

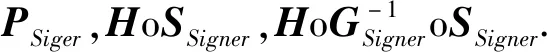
(1)计算：

(2)计算：

(x1,…,xn)=Q-1(y1,…,ym)=

(3)计算：

(4)计算：

GSigner(x1,…,xn)=

(g1(x1,…,xn),…,gn(x1,…,xn))=

(g1,…,gn)

(5)计算：

将(v1,…,vn)和(vg1,…,vgn)级联，得v1,…,vn‖vg1,…,vgn即为消息(u1,…,um)签名.

验证者收到消息(u1,…,um)和签名v1,…,vn‖vg1,…,vgn，对签名进行验证：

(2)将外部签名(v1,…,vn)代入签名者的公钥HoSSigner，得

(h1,…,hn)=HoSSigner(v1,…,vn)

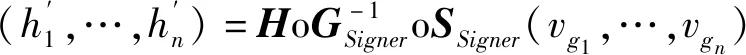
3.2 性能分析

从表2可以看出，随着参数的增大，签名和验证所耗时间均有所增加；相对于原有模型，新模型下所耗时间主要体现在签名的验证，特别是大参数时的签名验证，新模型所耗时间增加较大，这主要因为新模型下，签名验证由原有模型的一个公钥验证增加为两个条件，每判断一个签名的合法性至少需要计算3次，加之所增加的验证条件为非线性的公钥方程，因此，越大参数对新模型的影响越大.而对于签名的产生，较原有模型，新模型所耗时间增加较小.

表2 MI在原有模型及改进模型下签名验证时间对比

为进一步说明参数对时间的影响，按照不同参数给出图4～7的时间对比.

由图4至图7可以看出：

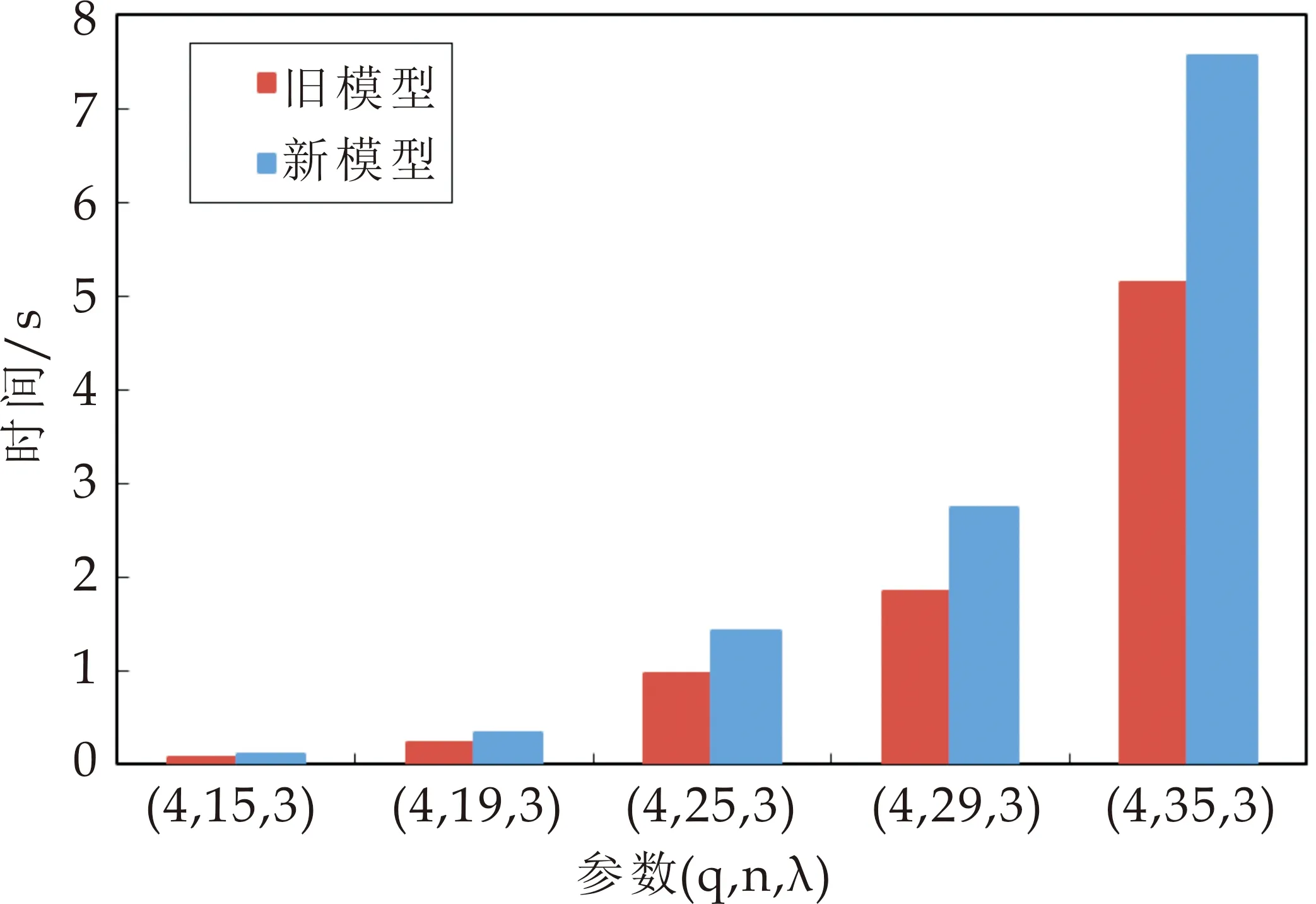
图4 (q,λ)=(4,3)，原有模型和改进模型下签名时间对比

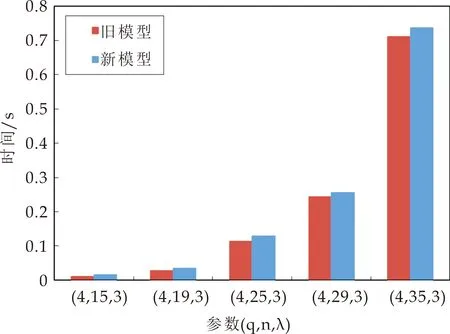
图5 (q,λ)=(4,3)，原有模型和改进模型下验证时间对比

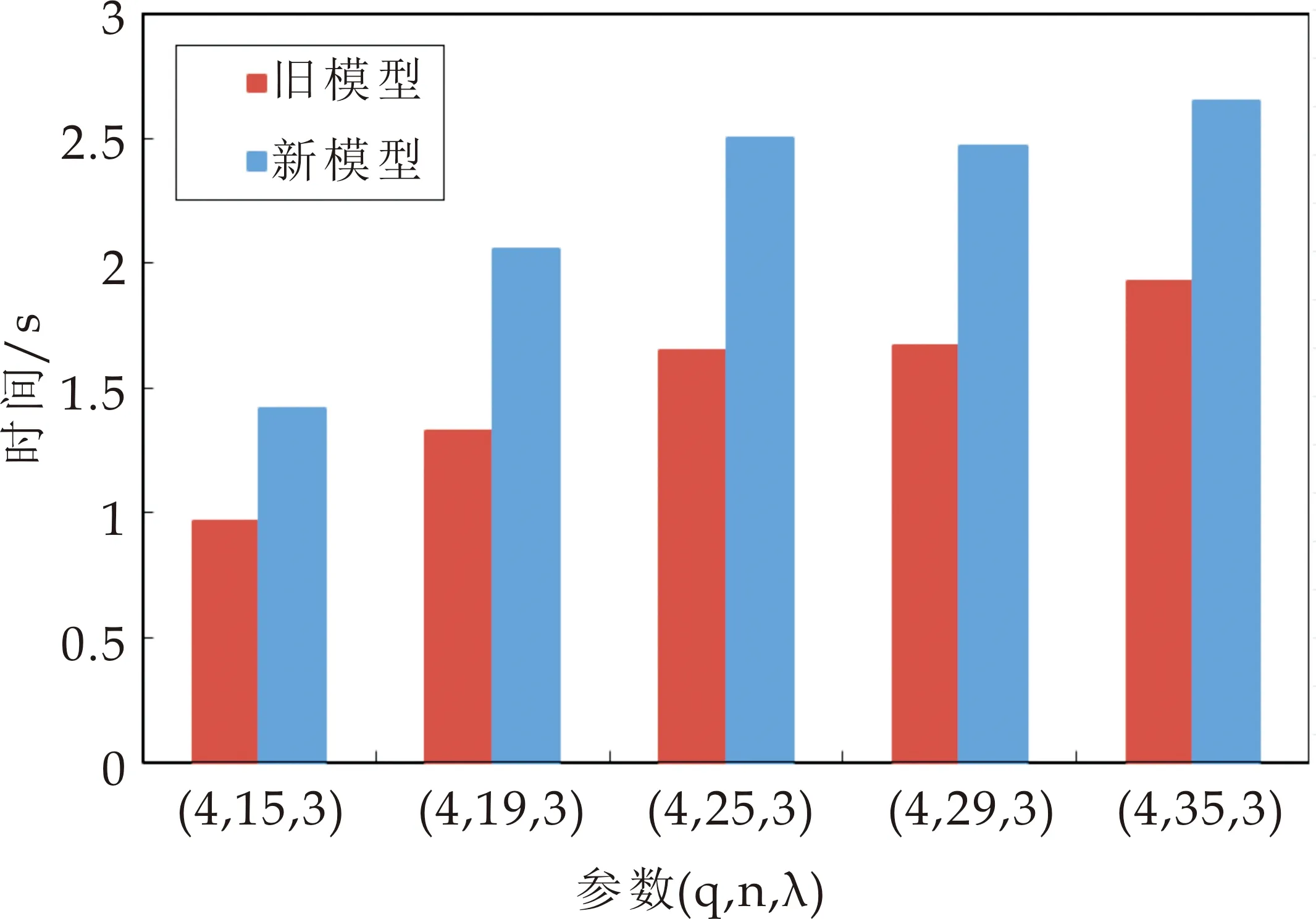
图6 (q,λ)=(25,3)，原有模型和改进模型下签名时间对比

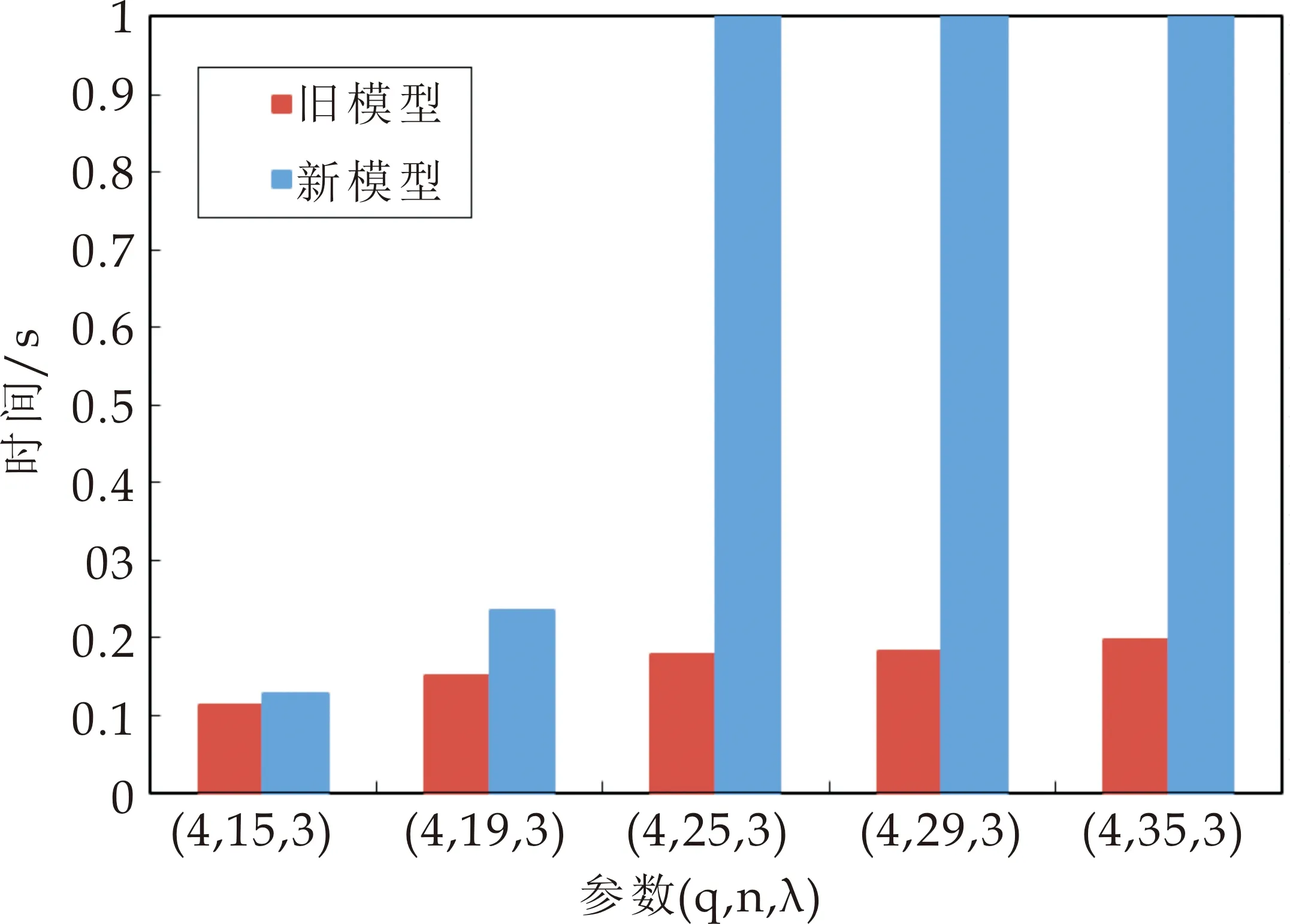
图7 (q,λ)=(25,3)，原有模型和改进模型下验证时间对比

(1)取(q,λ)=(4,3)，从图4和图5可以看出，新模型下的MI签名及验证时间较原模型下的时间基本相当，但有增长趋势.考虑到n是关于方程的数量，如果继续增加n的取值，签名和验证的时间均会大幅度增加；

(2)取(q,λ)=(25,3)，从图6和图7可以看出，q取值均略小时，新模型较原有模型下所用时间基本相当，增加不多，但是对于大数值的q，新模型中验证的时间是原模型的近百倍，这说明，大参数q的取值对新模型下方案影响较大.因此，新模型中应根据具体情况适当控制q的取值，以至于获得合理的签名和验证时间.

(3)不管是新模型还是原模型，λ的取值对签名时间和验证时间没有太大影响.

综上，原有模型以及改进模型的签名验证时间都随着参数的增大而变长，而改进模型下所用签名和验证都比原有模型所用时间有所增加，特别是签名时间，这是源于改进模型中签名由原来的一部分增加为二部分构成.验证时，验证公钥由原来的一个条件增至为两个.但改进模型比原有模型可抵抗伪造签名攻击，具有更高的安全性.

4 结论

基于线性化分析思想的伪造签名攻击是分析多变量公钥密码体制的一种常用且有效的分析方法，多变量公钥密码体制的原有签名模型在最初设计时还未遇到如线性化分析类的攻击，因此在涉及到具体方案时屡被攻破.为克服原有签名模型的设计缺陷，本文提出一种更为安全有效、可有效抵抗此类伪造签名攻击的多变量签名模型.该方法是在原有模型的基础上，通过增加额外公钥，将单一的公钥验证增强为必需结合内部节点信息进行验证，从而有效遏制基于线性化分析思想的伪造签名攻击带来的的潜在危胁.本文最后以经典方案MI为例，对原有模型和改进模型进行了对比分析，分析显示，改进模型可有效抵抗此类伪造签名攻击，为量子时代安全的数字签名方案的设计和研究提供了有益补充.