面向临近空间目标拦截的预测命中点设计方法
2020-10-12尹中杰朱柏羊韦文书安帅斌
尹中杰,刘 凯,朱柏羊,韦文书,安帅斌
(1. 大连理工大学航空航天学院,大连 116024;2. 辽宁省空天飞行器前沿技术重点实验室,大连 116024; 3. 北京空天技术研究所,北京 100074;4.中国运载火箭技术研究院,北京 100076)
0 引 言
近年来,随着高超声速技术的发展,以美俄为代表的军事大国正在大力发展临近空间高超声速武器[1]。由于高超武器具有飞行速度快、机动能力强、稳定跟踪难度大的特点,导致防空反导作战面临巨大挑战。因此,以美国为代表的世界大国开始聚焦高超声速武器防御技术。2018年美国导弹防御局(MDA)授出21份“高超声速防御武器系统概念”研究合同用于提高临近空间防御能力[2],其中较为引人注意的是3个基于高超声速平台的临近空间目标拦截方案,分别是波音公司的“针对高超声速武器的超高声速拦截器概念(HYVINT)”、通用原子电磁系统公司的“超高速拦截器系统”、德雷伯实验室的“超高速吸气者(HSAB)”。由于高超声速平台具有快速响应、射程远以及中段机动修正能力强的优势,可有效解决传统火箭动力拦截系统反临近空间高超声速目标的瓶颈问题,是后续发展中具有潜力的一类拦截方案。
在临近空间目标拦截方案中,预测命中点设计问题由于因为存在可行解搜索耗时长、拦截误差大的问题被广泛的研究。为进一步发挥高超拦截平台的射程远的优势,需要针对作战需求基于拦截平台的动力学特性重新设计预测命中点规划方法。
预测命中点是攻击弹、拦截弹同时间到达的一点,预测命中规划需要在拦截弹发射前,通过算法计算出合理的拦截点,并为拦截弹装订相应的诸元,使得拦截弹准时精确的飞抵预测命中点。在该方面,国内外学者普遍针对火箭动力拦截弹设计基于标准弹道族的预测命中点规划方法。
基于标准弹道族的预测命中点设计是指拦截方离线获得拦截覆盖区域得到标准弹道族,并通过调整拦截弹发射方位角形成等时间拦截曲面,并结合目标预报弹道筛选时间相同、位置重合相遇点的方法。该计算方法可以针对不同类型的目标飞行器快速有效地寻找准确的预测命中点。
在标准弹道族设计方面,文献[3-4]通过设计攻角指令设计完成了基于火箭动力的抛物线、直线标准弹道族,上述两种弹道设计方式具有方法简单、可行性强的特点。但是由于弹道的物理特性的因素,上述两种弹道并不能很完整的囊括拦截平台的所有拦截覆盖范围,存在覆盖区域有缺失的问题。文献[5]首先对拦截需求进行分析,引入性能指标,优化出指标最优拦截弹道,组成针对不同优化指标的多个标准弹道族。这种设计方法可以针对不同拦截状况,针对拦截需求选取相对应的标准弹道族进行更有针对性的预测命中点搜索。同时由于该方法有多个标准弹道族,可以在某一弹道族搜索失败后,切换至另一弹道族进行搜索,从而提高拦截成功率。并且通过弹道族叠加,在拦截覆盖范围上相较于文献[3-4]具有一定优势,但是通过弹道优化算法并不能优化出拦截空域最大的标准弹道族,所以同样无法克服无法囊括所有拦截覆盖范围的问题。
在搜索算法方面,文献[6]采用迭代发射诸元的方式解算预测命中点。通过假设初始的攻角、拦截时间获得弹道,通过位置偏差迭代攻角、时间修正量,从而逼近发射诸元正确值。这种方法采用在线求解弹道并修正误差的方式,具有拦截误差小的优势,但因为解算诸元较多存在遗漏可行解的问题。文献[7-8]针对弹道导弹被动段拦截,假设弹目距离是单调递减的,基于斜距迭代的方法,获得相应的发射诸元从而获得拦截弹弹道。但是临近空间高超目标相较于弹道导弹具有极强的机动能力,能够进行大范围的机动,拦截阵地与目标的斜距可能并不单调。预报弹道上可能存在有多个斜距相同的点,会导致迭代出的发射诸元存在偏差,致使拦截失败。同时由于搜索算法并未考虑标准弹道族内各弹道之间存在的时间、空间规律,没有设置对应的弹道搜索区间筛选、导致需要对标准弹道族内的弹道逐一搜索,导致计算耗时长,方法存在局限性。
针对以上问题,本文瞄准基于吸气式高超声速平台的临近空间目标拦截概念方案,开展预测命中点设计问题研究,基于拦截空域最大原则,结合吸气式动力拦截平台的动力学特性构建标准弹道族,在对目标预报弹道搜索区间预处理的基础上,给出高超声速拦截平台的预测命中点高效搜索算法,快速完成预测命中点规划。
1 方案构想与吸气式拦截平台质点动力学建模
1.1 方案构想
新式反临近空间目标高超声速导弹由助推器、拦截平台、动能拦截器组成。助推器用于爬升段的助推工作,由固体火箭发动机提供动力。拦截平台为吸气式高超声速飞行器,其任务是搭载一枚或多枚动能拦截器,并将其运抵至导引头开机距离。拦截平台采用轴对称升力体构型,动力方面采用亚燃/超燃双模态冲压发动机,动能拦截器采用红外式侧窗导引头,具有不小于50 km的探测距离。
在装备拦截平台后,防御系统将大体按照如下的方式实施防御作战:
1)敌方的高超声速武器放射后,通过天基预警卫星探测目标,将预警信息传送给作战指挥系统。作战指挥系统将对目标进行威胁评估、资源分配,并引导地基雷达搜索、捕获和跟踪目标。作战指挥系统制定交战计划,向作战平台发送目标数据、弹道信息和发射指令。作战平台按照初始发射方位需求调整平台姿态,然后实施发射高超声速导弹指令,发射高超声速导弹。
2)高超声速导弹发射后,首先由助推火箭加速,助推到Ma4以上后,助推器分离,拦截平台启动吸气式动力发动机加速飞行至指定巡航高度/速度,然后依靠吸气式发动机高比冲优势的高超声速巡航飞行。飞行过程中,地面雷达站仍然实时跟踪来袭目标,并据拦截平台和来袭目标信息实时解算新的预测命中点信息和预设弹道信息并实时发送给拦截平台,拦截平台按照接收信息对飞行弹道进行修正,导引向新的预测命中点。
3)当拦截平台飞到预测命中点附近时,动能拦截器与拦截平台分离,拦截器立即用红外感应、跟踪、识别目标,确定瞄准点;在姿轨控发动机的控制下,自行接近目标,最后通过直接碰撞拦截并摧毁目标。
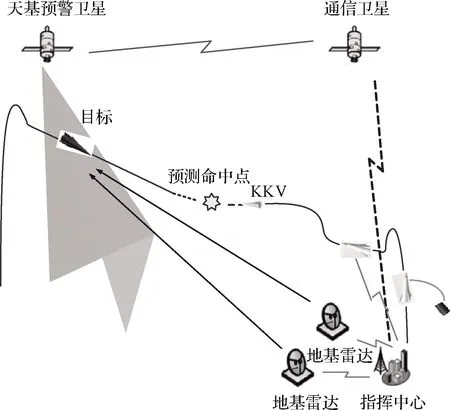
图1 拦截流程示意图Fig.1 Operational flow diagram
由于吸气式拦截平台所采用的超燃冲压发动机与固体火箭发动机存在很大的差异,而现有的标准弹道族设计方法并不能有效利用超燃冲压发动机工作特性,导致其无法为吸气式拦截平台设计出拦截空域最大的标准弹道族。除此以外,临近空间高机动目标相较于弹道导弹具有机动能力强的特点,传统的预测命中点解算流程在拦截临近空间高机动目标时存在解算速度慢,预测命中点实际拦截误差较大的问题。基于此,这里针对拦截平台动力学特性重新设计了标准弹道族与预测命中点规划方法,从而为基于吸气式高超拦截平台的预临近空间高机动目标拦截任务提供相关技术途径。
1.2 拦截平台质点动力学模型
模型在球形大地假设下,不考虑地球自转、在发射坐标系下建立质点动力学模型,根据拦截平台的特性完成坐标系的转化、受力分析并建立动力学方程[9]:
(1)
式中:x,y,z是发射系ox,oy,oz轴位置坐标;Vx,Vy,Vz发射系ox,oy,oz轴速度;θ,σ是发射系下弹道倾角、弹道偏角;D,L,Z,T分别是阻力、升力、侧向力、推力;Isp是比冲;Mfv是发射系与弹体坐标系的转换矩阵;Mfd是发射系与弹道坐标系的转换矩阵;h,r分别是高度、地心距;m为拦截弹质量;g为地表重力加速度;Re是地球半径。
转换矩阵具体形式如下:
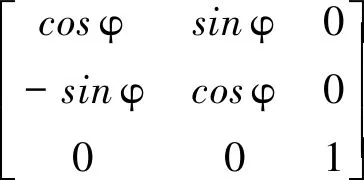
(2)
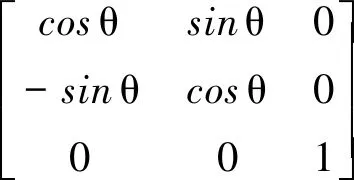
(3)
式中:υ为倾侧角,φ为俯仰角,ψ为偏航角,γ为滚转角。
1.3 预测命中点规划问题描述
预测命中点是预先计算来袭目标和拦截弹的飞行弹道,确定出瞬时遭遇点,即预测命中点,当预测命中点确定后,就导引拦截弹向其接近。基于此,预测命中点规划问题可以描述为:结合预报弹道与标准弹道族,通过搜索算法寻找满足时间约束、位置约束的拦截点。并为拦截弹装订相应的诸元,确保其准时精确到达拦截点。
约束条件如下:
(4)
式中:tf为预测飞行时间,xtf,ytf,ztf为预测命中点在发射坐标系下的位置。
2 基于吸气式拦截平台的预测命中点计算方法
2.1 吸气式拦截平台飞行策略设计
拦截平台发射后,共经历了固体火箭助推段与超燃冲压动力巡航段两种飞行状态,这里重点研究巡航阶段的飞行轨迹策略。
助推段设计采用单级运载火箭上升段指令生成规律进行设计。该方法将火箭上升过程分为若干飞行阶段,每段设定固定的程序角指令,这些指令由有限的参数决定,根据任务需求离线进行优化得到这些参数及其对应程序指令,装订在助推器系统中,上升段飞行过程中利用姿态控制系统实现程序指令即可。为寻求弹道轨迹的快速生成,将整个上升段分为3段,包括垂直上升段(0~T1),负攻角转弯段(T1~T2),重力转弯段(T2~T3)。
拦截弹全程飞行攻角近似公式为:
(5)
(6)
(7)
式中: 1/v0为推重比,αm是最大负攻角幅值,tm为负攻角值最大时刻,T2为负攻角转弯段,可以自由设置;T3为固体火箭燃料耗尽时间。
巡航飞行初始状态为助推段的末状态,在巡航段动力由超燃冲压发动机提供,推力通过数据插值得到,即T=T(q,kr,Ma),其中,q为动压、kr为推力调节阀门开度、Ma为马赫数。巡航段考虑拦截平台的飞行特性,要求拦截平台尽可能处于等高等速的飞行状态。为满足拦截需求,可以基于飞行高度将弹道分为平飞段与爬升段。
由于巡航速度大于助推段结束时的速度,这要求拦截平台首先要加速至规定速度,再转入等速飞行状态。在加速飞行过程推力为超燃冲压发动机所能提供的最大值,即T=Tmax。
等速飞行状态,为使速度保持恒定,因此有
(8)
1)平飞段
h=r-Re
(9)
可以对x,y,z求导并再对Vx,Vy,Vz求导,获得高度对攻角的二阶导数变化率:
(10)
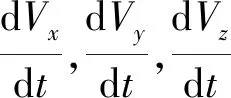
(11)
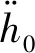
(12)
式中:dk是搜索方向,则令
(13)
即:
(14)
这里:
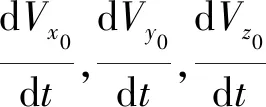
2)爬升段
爬升段是指拦截平台爬升至指定高度的一段飞行过程,可以细分为定攻角爬升段、直线爬升段、平滑过渡段三个部分。
首先,拦截平台在定攻角爬升段通过大攻角增加升力改变弹道倾角,从而使得拦截平台具有爬升能力。当弹道倾角达到预设值后,通过直线爬升的方式爬升至一定高度。为使拦截弹道保持直线爬升,需要弹道倾角变化率恒为0°/s,弹道倾角变化率表达式为:
(15)
可以设置攻角的迭代初值α0,通过牛顿迭代,即:
(16)
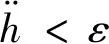
最后通过平滑过渡段,通过以飞行高度为自变量,弹道倾角为因变量的过渡函数,获得弹道倾角的程序指令。
φ(h)=
(17)
θd(h)=φ(h)θ1+(1-φ(h))θ0
(18)
式中:hmax为拦截高度,hmin为指定的平滑段起始高度,h为实际高度,θ0为平滑段起始弹道倾角,θ1为期望弹道倾角,由于等高等速的设计需求,在平滑末端在弹道坐标系下期望弹道倾角θ1=0,弹道倾角指令可以简化为:
θd(h)=(1-φ(h))θ0
(19)
为了将弹道坐标系下的弹道倾角指令转化为发射系下的弹道倾角指令,需要通过坐标转换矩阵,通过转化获得:
(20)
(21)
式中:δd为弹道系下弹道偏角,由于拦截空域是由一束存在于同一平面内的标准弹道族通过旋转发射方位角的方式获得,所以υ≡0°。获得在发射坐标系下的弹道倾角θ′后,通过与当前实际的发射坐标系弹道倾角θ相减做差,基于迭代步长Δt,可以得到弹道倾角的变化率:
(22)
发射坐标系下弹道倾角变化率还可以表示为:
(23)
即可通过弹道倾角变化指令完成攻角的迭代。
2.2 拦截平台标准弹道族设计
高超拦截平台采用火箭助推垂直发射,按照相应的攻角指令完成助推段飞行。助推段结束后,通过超燃冲压发动机加速至指定速度并达到指定高度。
巡航式拦截器射表由两种不同的弹道族组成,分别是巡航弹道族与爬升弹道族。
巡航弹道族是指助推段结束后,通过超燃冲压动力直接加速至指定速度,爬升至拦截高度,并在拦截高度上等高等速飞行,并由不同拦截高度的巡航弹道完成巡航弹道族。该弹道族的初始高度变化率为拦截平台允许的最大高度变化率,所以能在最短的时间到达指定拦截高度,所以在初期有较大的拦截空域,但是在后期,由于爬升时间过早,导致部分弹道高度过高,比冲较低,存在拦截航程较小的问题,所以单一由巡航弹道所组成的标准弹道族不能很好的覆盖拦截平台所有的拦截空域,可以通过引入采用其他飞行策略的标准弹道族组成标准弹道族群,从而弥补巡航弹道族未覆盖的拦截空域。
为弥补巡航弹道族在拦截高度较高时拦截航程较小,无法覆盖全部的拦截区域的问题,引入了爬升弹道族。爬升弹道在助推段结束后,首先在燃料最省的基准弹道飞行,在某一时刻爬升,当高度满足拦截高度再进行等高飞行。并由不同爬升时刻、不同拦截高度的爬升弹道组成爬升弹道族。爬升弹道利用基准弹道比冲大的特点,可以获得较大的航程。
由于巡航式高超拦截平台具有宽速域特性,可以选择不同的速度进行飞行。那么在同一个拦截点,采用不同飞行速度的拦截平台将有不相同的拦截时间。基于此可以设计出多个不同飞行速度的标准弹道族组成标准弹道族群,通过扩大搜索范围的方式提高拦截成功率。
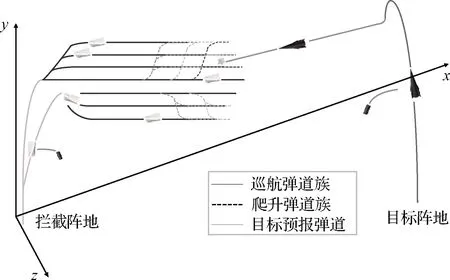
图2 拦截示意图Fig.2 Interception diagram
2.3 拦截搜索区间计算
为提高搜索算法的运算效率,需要基于吸气式拦截平台动力学特性进行有针对的减小搜索范围,同时为保证拦截器处于逆轨拦截状态,且不存在不同时间、航程相同的问题,需要对目标飞行器进行拦截区域划分,并分段讨论。
首先,获得航程与时间的关系,筛选出目标—阵地航程单调递减区间,确定一定时间内的航程极值点个数n与相对应的时间tn,由此将拦截时间分为n+1段,单调时间段为t∈[ti-1,ti],i∈[0,n+1],由此确保在规定时间段内,航程变化是单调的,不存在航程相同的可能。
由于预测命中点存在时间与空间上的约束,结合预测命中点规划需求,可以将其转化为带有航程约束、高度约束的拦截时间与发射方位角求解。则可以寻找在拦截时间段内满足航程约束的弹道集合,再从弹道集合中筛选出满足高度约束的弹道,从而根据满足航程、高度约束的拦截点位置计算出拦截时间与拦截平台发射方位角。
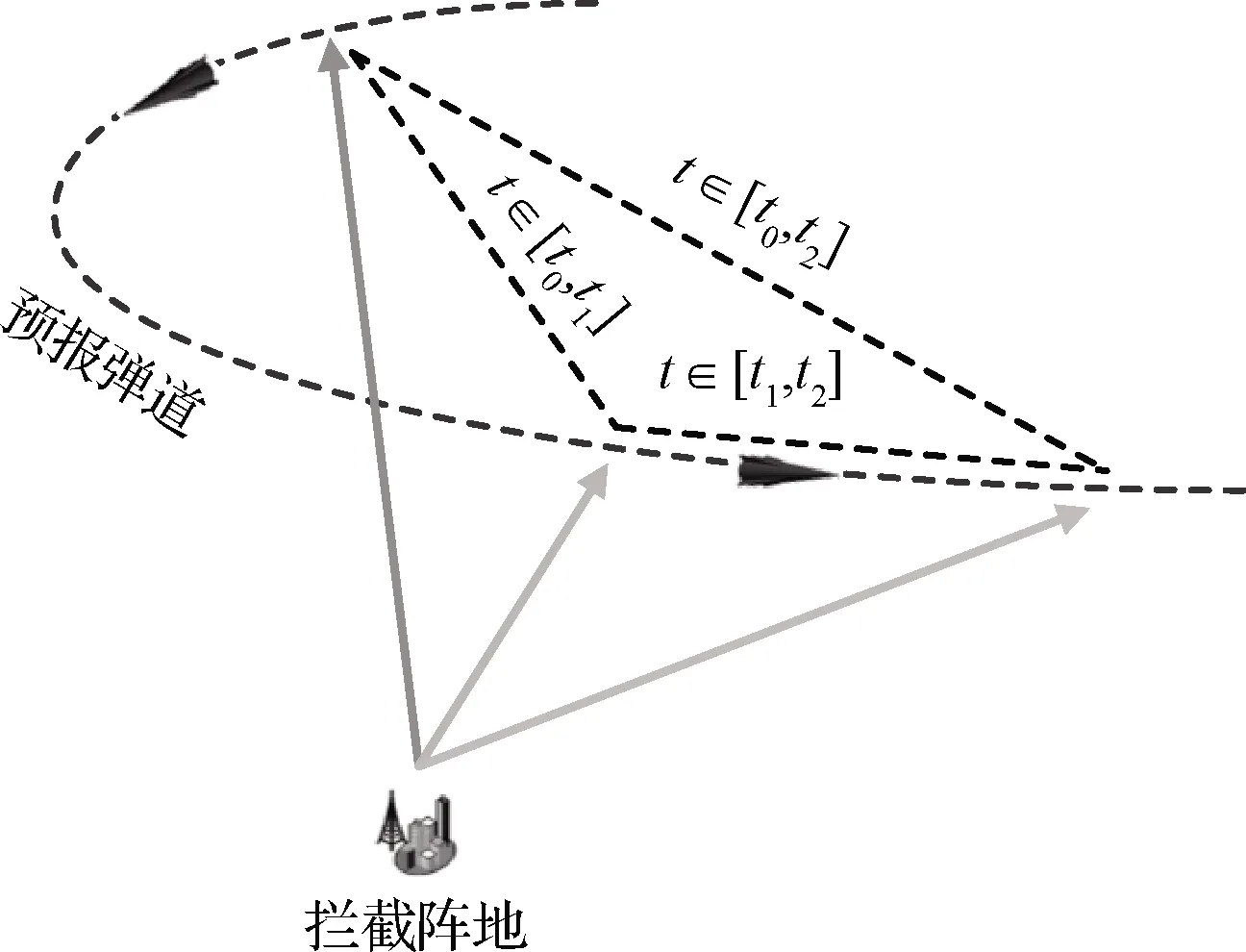
图3 时间预划分示意图Fig.3 Time division diagram
由于拦截平台动力学特性与标准弹道族构成方式,同一速度下标准弹道族内各条弹道,在相同时间航程差较小。而基准弹道(燃料最省弹道)又具有最远的航程,可以覆盖本弹道族内在规定时间区间所有弹道的航程区间。
所以可以判断在某一区间段内目标航程—时间与基准弹道航程—时间曲线是否存在交点,若存在交点,可以认为在标准弹道族中存在满足航程约束的多条弹道,具有筛选到满足高度约束的预测命中点的可能性。
交点解算流程如下:
1)判断基准弹道与目标弹道在某一时间区间t∈[ti-1,ti],i∈[0,n+1]有没有航程重叠的区域。
如果:
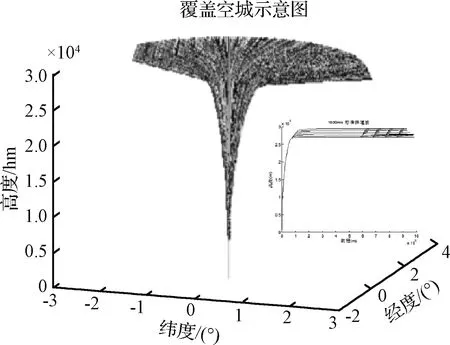
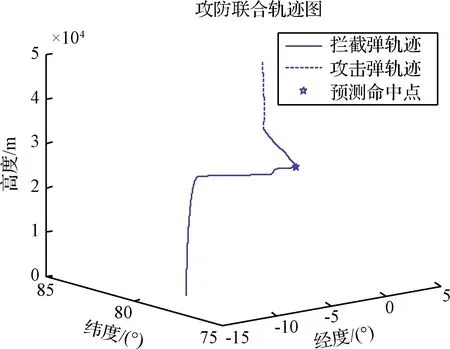
R1 (24) 则两个区间没有交点,搜索结束。其中R1指基准弹道的航程最大值,R2指目标的距离阵地航程最小值。 否则,找出两者的航程重叠区域 tqj=[t2(R1),t2(R2)]∩[t1(R2),t1(R1)] (25) 式中:t2(R)是指目标航程为R的时间,t1(R)是指拦截平台航程为R的时间,tqj为筛选后精简的时间区间。 ΔR=Rgj(tqj)-Rlj(tqj) (26) 式中:Rlj(tqj)指拦截平台在时间区间tqj内的航程区间,Rgj(tqj)指目标在时间区间tqj内的航程区间,ΔR为相对距离。 2)计算交点处飞行时间,令: a=sgn(ΔR)′ (27) 由于ΔR是弹目的相对距离,sgn(ΔR)=1表示该时刻弹目相对接近,sgn(ΔR)=-1表示该时刻弹目相对远离,则在预测命中点ΔR的符号应该发生切换,sgn(ΔR)导数的幅值变化±2为即: (28) (29) (30) [t0,R]=(A/B)′ (31) 式中:t0为交点处的时间,R为交点处的航程。 通过以交点处的时间t0作为时间迭代的初始值,并通过将t∈[t0-Δtm,t0+Δtm]与单调区间取交集的方式获得搜索区间,Δtm为可设置的预估时间。 标准弹道族由两种弹道组成,其中全部的等高巡航弹道可以看作一束弹道,二次爬升时刻tmin为0 s;而爬升弹道中,相同爬升时刻tmin的弹道亦可以看为一束弹道。 在一束弹道中,由于爬升时刻相同,速度相同,在相同时间飞行高度最低的弹道航程最远,飞行高度最高的弹道航程最近。则基于这一特性,由最低端的弹道开始,向最高弹道逐一搜索,以爬升起始时间tminlj,燃料耗尽时间tmaxlj_i为拦截区间ti∈[tminlj,tmaxlj_i],将拦截区间ti∈[tminlj,tmaxlj_i]与搜索区间取交集为t∈[tmin,tmax_i],如果t∈[tmin,tmax_i]为非空集,并且: (32) 式中:Rgj为目标与拦截阵地的航程,Rlj为拦截平台与拦截阵地的航程。通过迭代的方式搜索Rgj=Rlj的时间,即: F0=Rgj(tmin)-Rlj(tmin) (33) F1=Rgj(tmin+Δt)-Rlj(tmin+Δt) (34) (35) 满足|(Rgj(t0)-Rlj(t0))|><ΔL,可获得拦截时间t0。 由于目标的航程在搜索区间内单调递减,而一束弹道内相同时间高度越高,航程越短,则在下一搜索过程tmin=t,并重复上述过程,若: Rgj(tmin) 或 Rlj(tmax) 则结束在这一束弹道的搜索。 获得满足航程约束的拦截弹道后,可基于目标预报弹道中的高度信息筛选出符合拦截要求,并且距离误差最小的拦截点作为预测命中点,并计算发射诸元,发射诸元包括飞行速度V,发射方位角Af,攻角α。发射方位角解算流程如下: B=arccos(sinλ0sinφf+cosφ0cosφfcos(λf-λ0)) (36) A1=(sinφf-cosBsinφ0)/(sinBcosφ0) (37) A2=(sin(λf-λ0)cosφf)/sinB (38) (39) 式中:λ0,φ0是拦截阵地经纬度,λf,φf是预测命中点经纬度。 除了发射方位角Af,为确保拦截平台能够满足约束,还需要基于离线获得的标准弹道族中,距离预测命中点最近的拦截弹道获取拦截爬升时间、拦截高度信息。从而获得每一时刻的攻角信息,从而为拦截平台装订发发射诸元完成预测命中点规划。 图4 程序框图Fig.4 Program chart 考虑拦截方利用探测系统提供的弹道数据预报了未来600 s的攻击弹弹道,结果如图5所示。 表1 仿真输入数据Table 1 Chemical composition of experimental alloy 图5 目标预报轨迹Fig.5 Target prediction trajectory 图6 目标距离拦截阵地航程Fig.6 Target and intercept position range 由图6可知目标距离拦截阵地的斜距先变小,再变大,再变小,考虑到拦截器仅具有逆轨拦截能力,所以搜索区间为两个航程—时间成反比的区间,即t1∈[0,440],t2∈[459,600]。 针对高超拦截平台,这里基于冲压发动机特性设计了包含巡航弹道与爬升弹道的标准弹道族。 为验证包含巡航弹道与爬升弹道的标准弹道族是否具有覆盖所有拦截区域的能力,这里引入直线弹道。通过设置固定拦截高度,对比航程与爬升至指定高度的时间,验证标准弹道族设计的正确性。 假设拦截高度为29.5 km,拦截平台飞行速度1800 m/s,直线爬升弹道的弹道倾角为0.4°。 图7 航程—时间曲线Fig.7 Range VS time 图8 高度—时间曲线Fig.8 Height VS time 通过对比图7和图8发现,巡航弹道在拦截初期能够较早的爬升至预设拦截高度,而爬升弹道具有航程上的优势。直线弹道在航程与爬升至拦截高度的时间上均无优势,这也从侧面说明了采用两种弹道相组合的标准弹道族能够有效的扩展拦截空域。 图9 覆盖空域示意图Fig.9 Dchematic diagram of covered airspace 拦截平台为巡航式飞行器,由超燃冲压发动机提供动力,飞行攻角范围为α∈[-4°,6°],为确保发动机正常工作,需要动压满足约束q∈[30 kPa, 70 kPa]。结合拦截平台的飞行速度约束V∈[1800 m/s, 2100 m/s],拦截高度被限制为H∈[26 km, 30 km]。 基于以上限制,假设前期获得4个拦截射表,飞行速度分别为1800 m/s,1900 m/s,2000 m/s,2100 m/s,最大拦截允许误差为1 km,并设置搜索区间为t1∈[0 s,440 s],t2∈[459 s,600 s]。 在t1∈[0 s,440 s]区间,没有搜索到可行解。在t2∈[459 s,600 s]区间,搜索到可行解。采用速度1800 m/s标准弹道族,拦截时间为503 s,发射方位角-19°,采用爬升弹道,切换时间为400 s,距离误差146 m,搜索时间小于0.1 s,如图10所示。 图10 轨迹示意图Fig.10 Track diagram 本文瞄准基于吸气式高超声速平台的临近空间目标拦截概念方案。结合吸气式动力飞行策略构建高超声速拦截平台的标准弹道族;通过将多约束拦截预测命中点设计问题分解为基于航程约束的拦截时间迭代计算问题和满足高度约束的拦截点的高效筛选问题,从而完成预测命中点规划,为下一代反导拦截系统提供潜在的技术途径。2.4 基于射程迭代的发射诸元解算

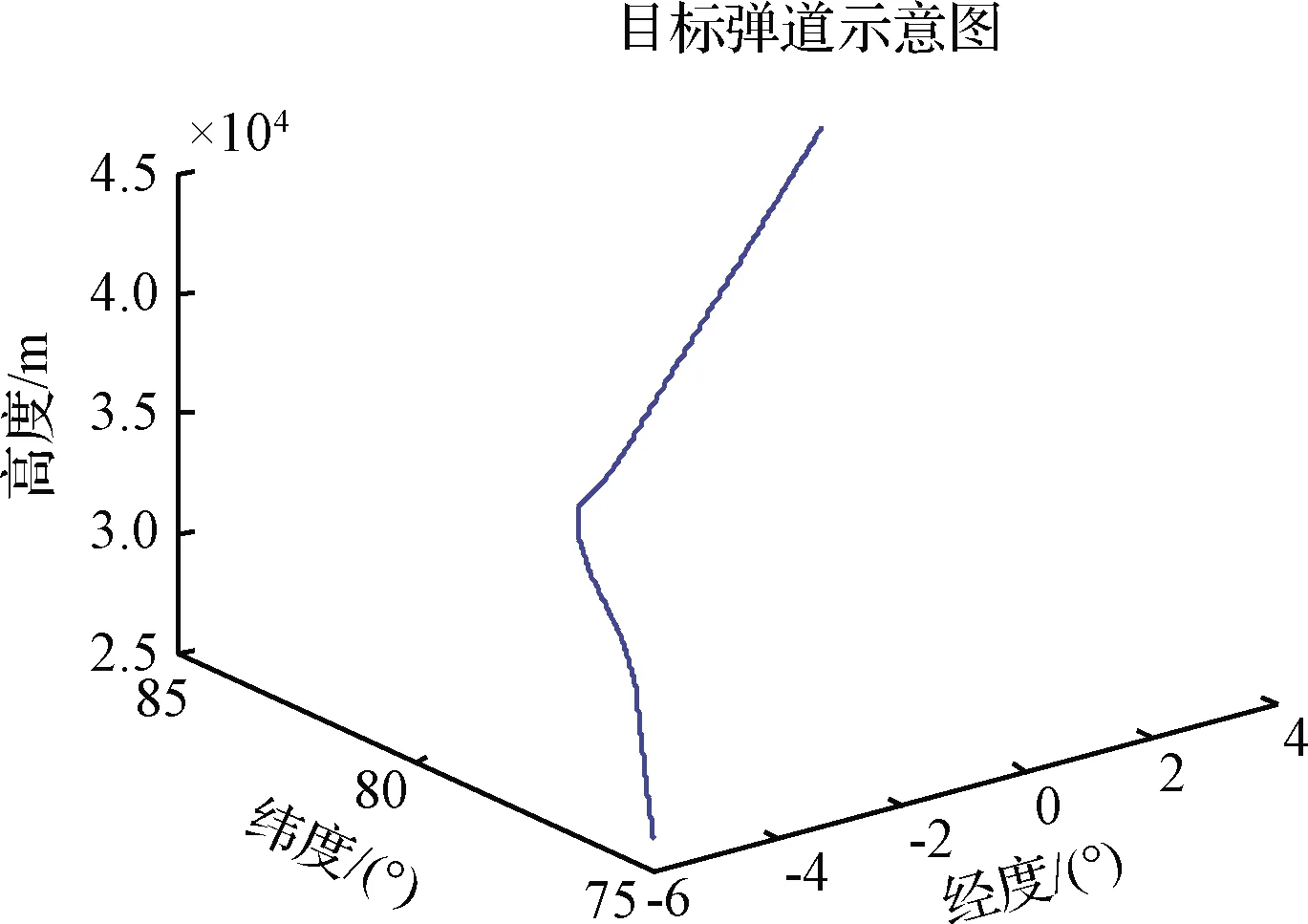
3 仿真分析
3.1 仿真输入
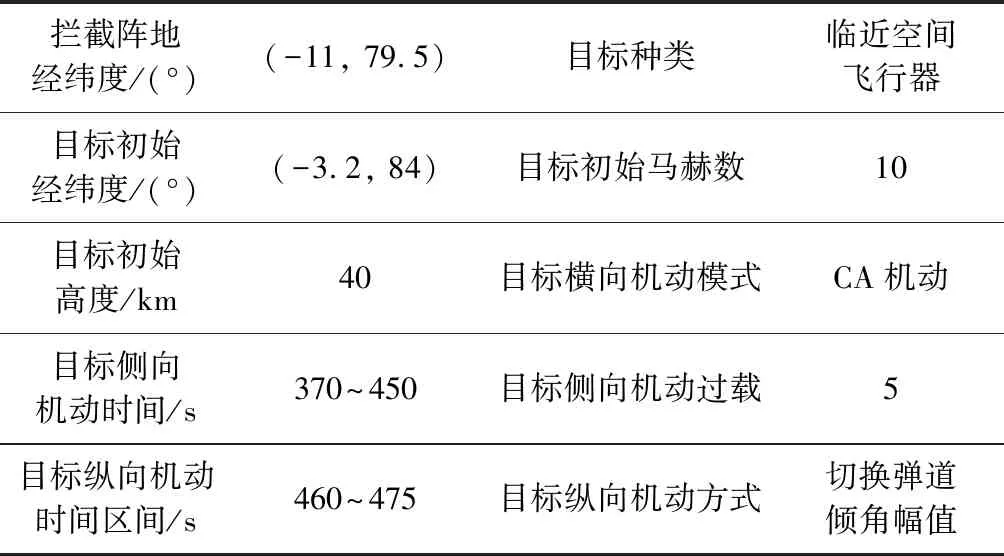
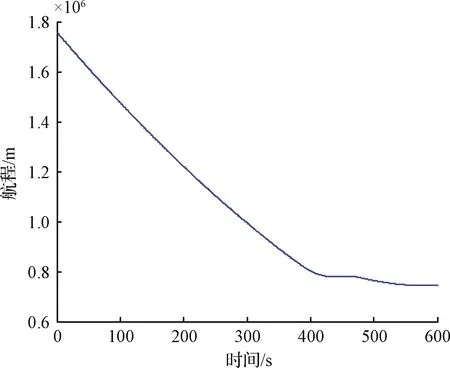
3.2 标准弹道族设计仿真分析
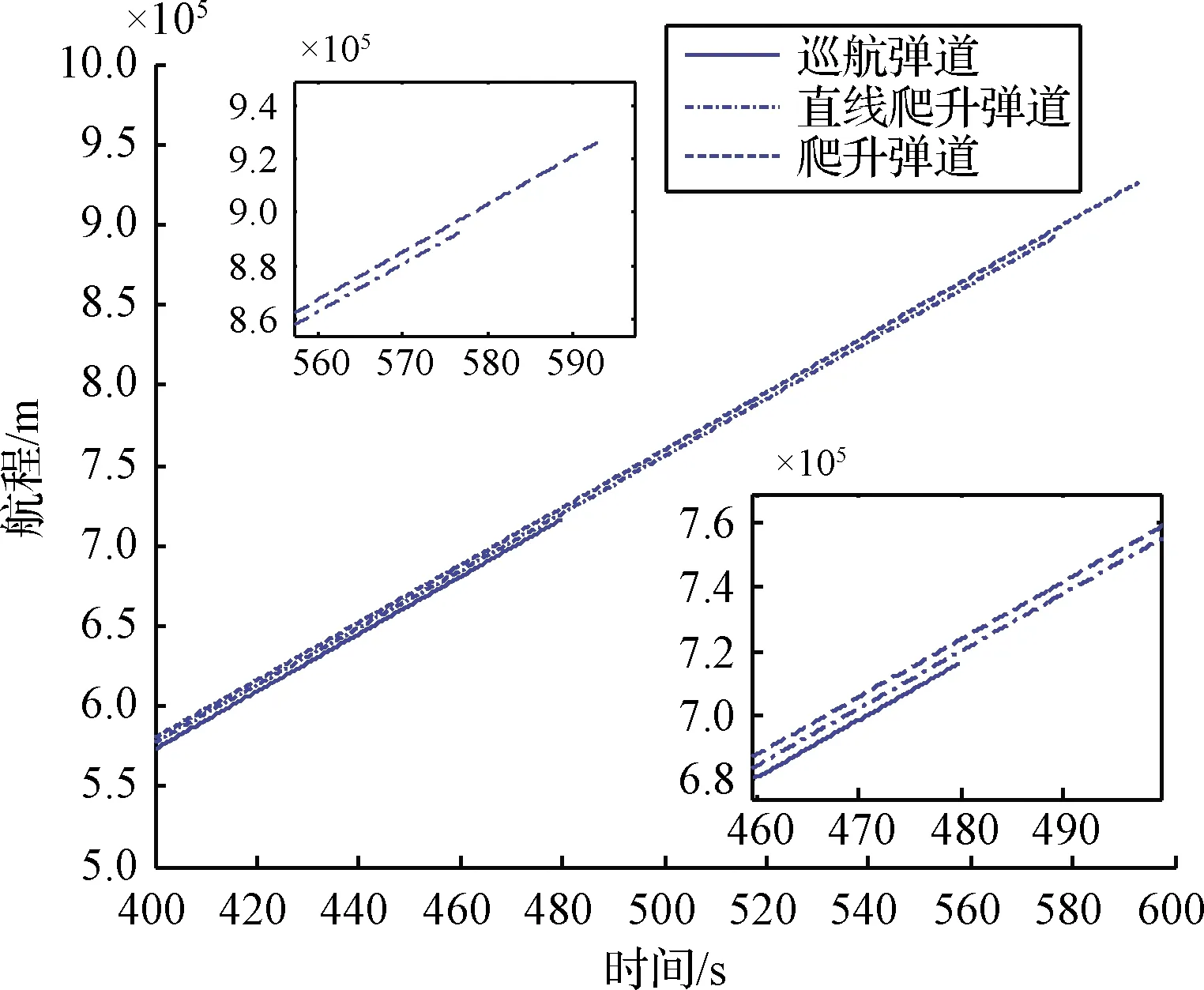
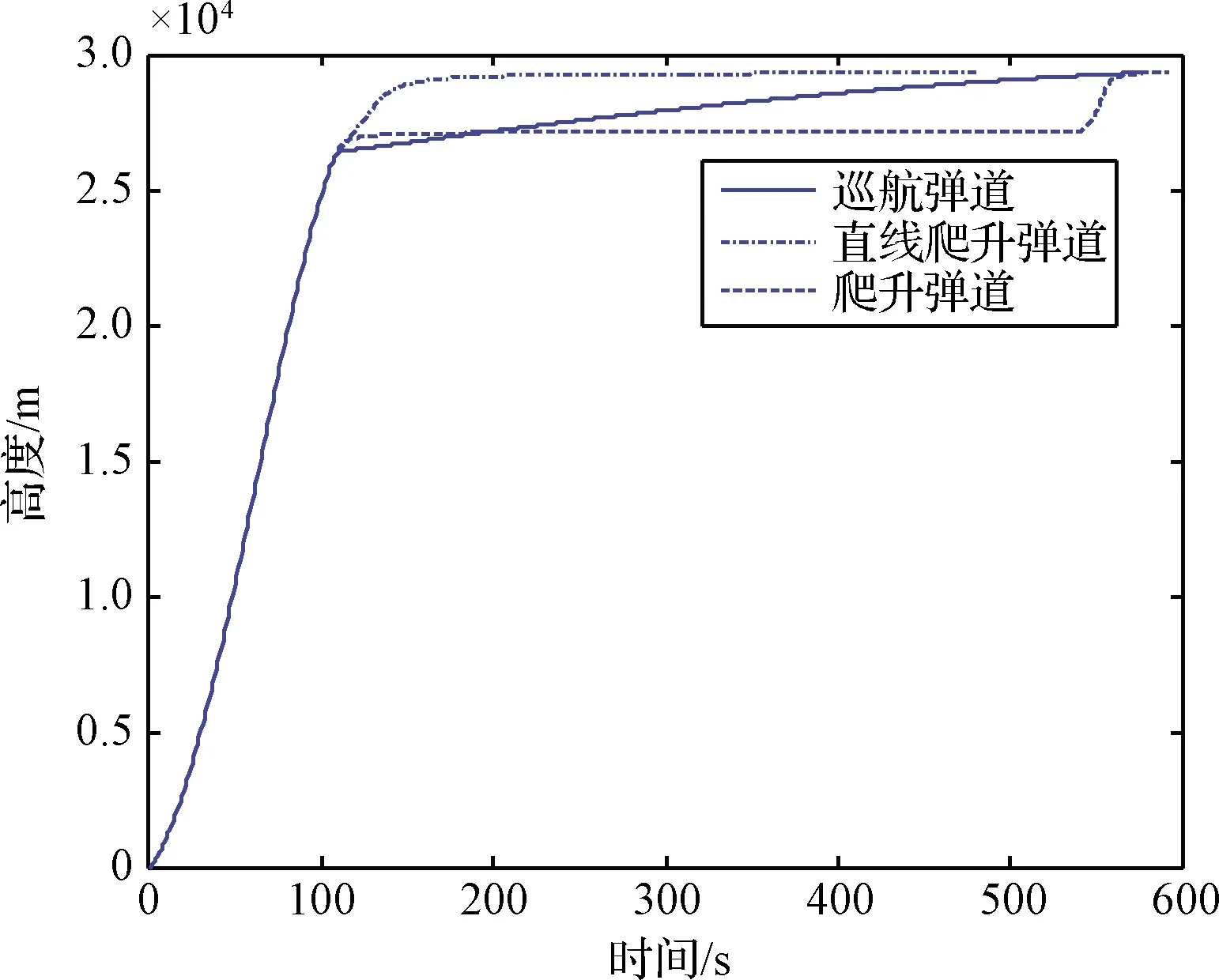
3.3 预测命中点规划仿真分析
4 结 论
