面向小推力变轨的天文组合自主导航方法
2020-10-12马广富黄庆龙彭玉明
马广富,王 伟,,张 伟,黄庆龙,彭玉明,张 晓
(1. 哈尔滨工业大学控制科学与工程系,哈尔滨 150001;2. 上海卫星工程研究所,上海 200240; 3. 上海市深空探测技术重点实验室,上海 200240)
0 引 言
小行星探测活动是当前国内外航天活动的重点和热点,包括小行星探测在内的多次深空任务也已纳入国家深空重大专项。小行星探测任务由于能量需求大,所以高比冲、长寿命、高可靠的电推进系统是工程任务实施的优选动力形式。采用电推进方式能有效增强探测器变轨能力,提高任务灵活性,降低任务成本等优势,但电推进方式给探测器带来一些新问题。电推进方式推力较小,需要长期连续开机工作,期间为确保推力方向正确且帆板对日定向,探测器与地面的通信无法保证连续可用,地面无线电导航方法无法为探测器提供可靠的导航信息。此外,电推进方式对连续小推力建模的不准确性,只依靠探测器自主轨道递推等方法应用受限,因此,采用小推力变轨的小行星探测器亟需一种能够提供实时连续、高精度导航信息的自主导航方法。
当前小行星探测工程任务主要依赖于天文光学图像测角方法进行自主导航,该方法对观测的目标天体约束限制较多,导致小行星探测器的导航信息不能满足实时连续高精度的需求[1-3]。本文在近年来深空导航领域新提出的直接获得探测器速度信息方法的基础上[4-6],结合测角导航方法,给出了一种适用于小推力变轨小行星探测器的组合自主导航方法。
基于电推进方式的小行星探测器,由于存在太空环境未知因素多、动力学环境变化大等因素,导航系统的状态具有不确定性强、状态模型变化较大等特点,这些因素对导航系统状态估计性能会有很大影响[7]。目前,国内外学者针对导航系统状态模型多变的情况,提出了采用多模型的状态估计方法[8-10]。交互式多模型算法(Interacting multiple model,IMM)是在二十世纪九十年代由Blom和Bar-Shalom提出,同时他们也对IMM算法做了大量改进研究[11-12]。IMM算法计算消耗适中,通过对各子滤波器估计结果融合输出作为滤波算法的初值,同时利用输出结果的交互概率实现各子滤波器的初始化,达到基于不同模型组合跟踪实际导航系统变化的效果。
在上述研究基础上,学者们对IMM算法提出了很多的改进[13-15]。Johnston和Krishnamurthy通过重新计算权值给出了新的IMM算法[16]。Li等[17]通过对IMM算法结构进行改进,提出了变结构的交互式多模型(VSIMM)算法,但是由于结构复杂,计算量加大,在实际应用中有一定的局限性。近年来,徐田来等融合参数自适应与IMM算法得到了新的IMM算法[18],但由于加入了参数自适应,算法的计算量较大。有些学者通过引入神经网络等智能算法计算IMM算法的模型转移概率[19-20],或者对各个子模型的参数做修正,进而更准确地对系统状态进行估计[21-22],上述这些针对IMM的改进方法计算效率不高,不利于在实际工程中应用。
当前针对基于电推进方式变轨的小行星探测器,在推力矢量不确定性较大、动力学环境未知因素多等情况下的导航状态估计问题研究尚少。本文针对持续小推力变轨的小行星探测器对导航系统自主性强、实时性高的需求,研究了一种小推力变轨的天文测角测速组合导航方法。首先,根据工程实践分析并建立了电推进变轨过程中的动力学模型,给出了天文光学图像测角融合天文光谱测速的组合导航方案;为了克服系统模型集合小、先验信息的不准确性对导航系统估计精度的影响,提出结合Sage-Husa自适应估计器的AIMM算法,以较少的的模型个数实现对实际状态的覆盖;同时结合UKF算法给出AIMM-UKF算法,以提高组合导航系统的鲁棒性和抗干扰能力。最后,通过数学仿真对天文测角测速组合导航系统的性能进行对比验证,分析本文所提出的导航方法的有效性。
1 天文组合导航系统模型
1.1 导航系统状态方程
依据轨道动力学分析,建立小行星探测器天文测角测速组合自主导航系统的状态方程。本文以小行星探测任务的巡航段为对象,在动力学建模时主要考虑的因素有探测器在飞行过程中的太阳、地球、小行星等天体引力,太阳光压摄动,探测器的修正推力等。
以J2000日心黄道惯性坐标系为基准,小行星探测器位置矢量设为r=[x,y,z]T,速度矢量设为v=[vx,vy,vz]T,则组合导航系统的状态变量可写为X(t)=[x,y,z,vx,vy,vz]T,此时系统状态方程可表示如下:
(1)
在第二行的方程中,第一项是太阳引力摄动,μS是太阳引力常数;第二项是主要行星的第三体引力摄动,ri表示第i个考虑的行星位置矢量,ui表示该行星的引力常数,M=1,2,3,…是所考虑的行星数量编号,rSi表示行星相对小行星探测器的位置矢量;第三项是探测器的太阳光压摄动。前三项是深空探测器一般都需要考虑的影响因素,第四项是探测器推力加速度项,一般地对推力加速度项是按某个小时段脉冲变轨的形式处理。但对于持续小推力变轨的小行星探测器,由于推力矢量长时间存在,需要考虑较多长期变化因素影响,有必要对模型做进一步的细化。
对于采用电推进方式的小行星探测器,根据工程实践分析经验,其推力加速度项模型可表示为:
(2)
式中:第一项是探测器的修正加速度,U是发动机的推力矢量,m是航天器的瞬时质量;第二项是推力常值偏差;第三项是在推力常值偏差外,呈有周期性缓变的推力偏差;最后一项是其他未建模误差,可按照高斯白噪声处理。Isp为发动机比冲;g0为海平面重力加速度。
基于上述分析,小行星探测器巡航段的轨道动力学方程如下:
(3)
式中:W是状态模型噪声。
1.2 导航系统量测方程
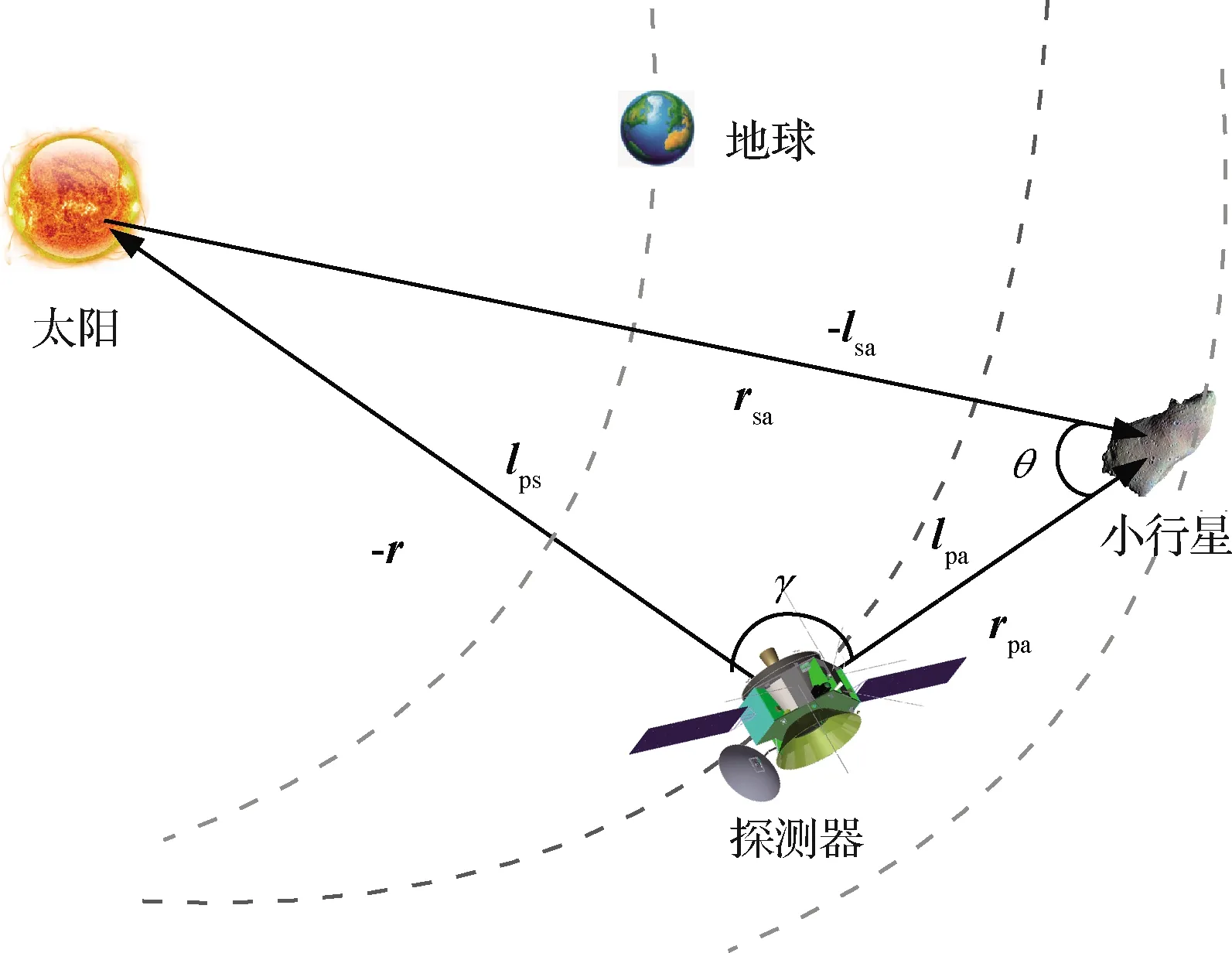
图1 测角导航原理示意图Fig.1 Principle of angle measurement navigation
在小行星探测器飞行过程中,导航目标天体的视星等将随着探测器逐步靠近小行星而慢慢变小,探测器上可通过高精度光学图像导航敏感器得到目标天体的图像,通过提取目标天体相对小行星探测器的视线方向矢量,即可获得探测器相对目标天体的角度信息。所得到的量测信息作为滤波估计器的输入即为天文测角自主导航[17]。以小行星和太阳为目标天体的测角导航方法其原理如图1所示。
基于上述分析,测角导航量测方程如下:
(4)
式中:r表示探测器在J2000日心黄道惯性系的位置矢量;lps表示探测器敏感期测量得到的太阳视线矢量、lpa表示探测器敏感期测量得到的小行星视线方向矢量;Vps、Vpa表示对应量测系统噪声。

图2 测速导航原理示意图Fig.2 Principle of velocity measurement navigation
小行星探测器在飞行过程中,相对空间中的太阳或者恒星会因为相对速度的多普勒效应,探测器上的光谱敏感器接收的光谱波长会产生漂移。依据多普勒原理,探测器敏感器在飞行过程中接收波长的漂移量与其静止时接收到的波长之比等于探测器相对太阳或者恒星的视向速度与光速之比。基于上述分析,可得到以小行星探测器相对太阳、2颗恒星的视向速度为量测的导航方案,其原理如图2所示。
测速导航量测方程如下:
(5)
式中:vSpe1,vSpe2,vSpe3分别表示探测器上光谱敏感器测得的相对太阳及2颗恒星的视向速度数值;r,v表示探测器相对太阳的位置、速度矢量;vStar1,vStar2和lStar1,lStar2分别表示2颗恒星在J2000日心黄道惯性系下的速度和视线方向矢量;V表示量测系统噪声。
综上,小行星探测器的导航量测模型可用如下一般形式描述:
Z=h(X,t)+V
(6)
2 组合导航算法设计
基于电推进方式变轨的小行星探测器,由于推力持续时间长、推力影响因素多、探测器的动力学环境变化大等因素,前述的组合导航系统不确定性强、状态模型变化较大,这些因素对导航系统状态估计精度会有很大影响。IMM算法利用多个子模型的模型集来描述系统可能的运动状态,对小行星探测器导航系统状态具有很好的跟踪效果。下文基于IMM算法,对其开展研究分析并给出改进的导航滤波算法。
2.1 IMM算法及其改进
交互式多模型算法包括四个部分:输入交互、滤波估计、模型更新及融合输出。
IMM算法利用多个子模型描述导航系统的可能运动状态,通过计算不同模型概率及其转移概率,完成导航滤波估计过程中的输入交互。输入交互后的数据经过导航系统滤波后,更新不同导航模型概率权值,并进而得到多个模型状态和对应协方差矩阵的融合值,最后通过滤波估计器融合输出导航系统状态的估计结果。
与单模型及其他多模型处理方法相比,IMM-UKF算法具有很强的交互性和自适应性,具有很高的效费比,有利于处理小行星探测任务中具有持续推力变轨、动力学环境未知因素多等情况复杂的导航状态估计问题。但IMM-UKF算法本身也存在一些局限性,由于导航系统模型概率是基于先验信息给出[23-24],而先验信息往往由于环境不确定性、存在量测噪声等因素,具有一定的不准确性,对导航系统的滤波估计精度会有较大的影响。
对于测角测速组合导航系统,为解决上述不准确性影响,保证交互式多模型中的模型集合覆盖系统的所有可能状态,IMM算法通常需要建立较大的模型集合,但是过多的模型会消耗探测器上很多的计算资源。为了减轻导航算法的计算量,匹配小行星探测器的计算能力,通过引入自适应参数估计器,在实际模型参数附近逼近真实的模型参数,实现对IMM算法进行改进并得到AIMM算法。AIMM算法可以利用较小的模型集合实现对实际组合导航状态模型的覆盖。
针对天文测角测速组合自主导航系统,本文将针对线性系统的Sage-Husa次优极大后验噪声估计器推广到非线性系统[25-26],得到非线性时变噪声无偏递推估计器,具体计算如下:
(7)
(8)
式中:
(9)
(10)
(11)
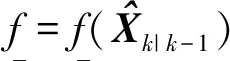
(12)
式中:遗忘因子b∈[0.95, 0.99]。
AIMM算法将利用Sage-Husa自适应估计器,对导航系统量测噪声误差进行自适应估计,从而增强IMM算法输出对导航系统状态模型的逼近,减小由于模型较少导致导航估计精度下降的影响。
2.2 滤波器模型集设计
在小行星探测器电推进持续变轨过程中,由于导航系统动力学环境变化大、推力矢量模型不精准等因素,导航系统的状态模型变化较大。结合前述AIMM算法,考虑在导航系统状态模型上引入一组系统噪声和观测噪声,设计滤波器的模型集。将式(3)和式(6)离散化处理,并引入子模型记号mi,则有如下滤波器模型集:
(13)
式中:W(k,mj)和V(k+1,mj)分别是系统状态模型和量测模型的噪声;j=1,2,3,…,N表示不同子模型序号,通过选取不同大小的量测噪声得到不同的子模型。
2.3 AIMM-UKF算法设计
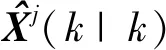
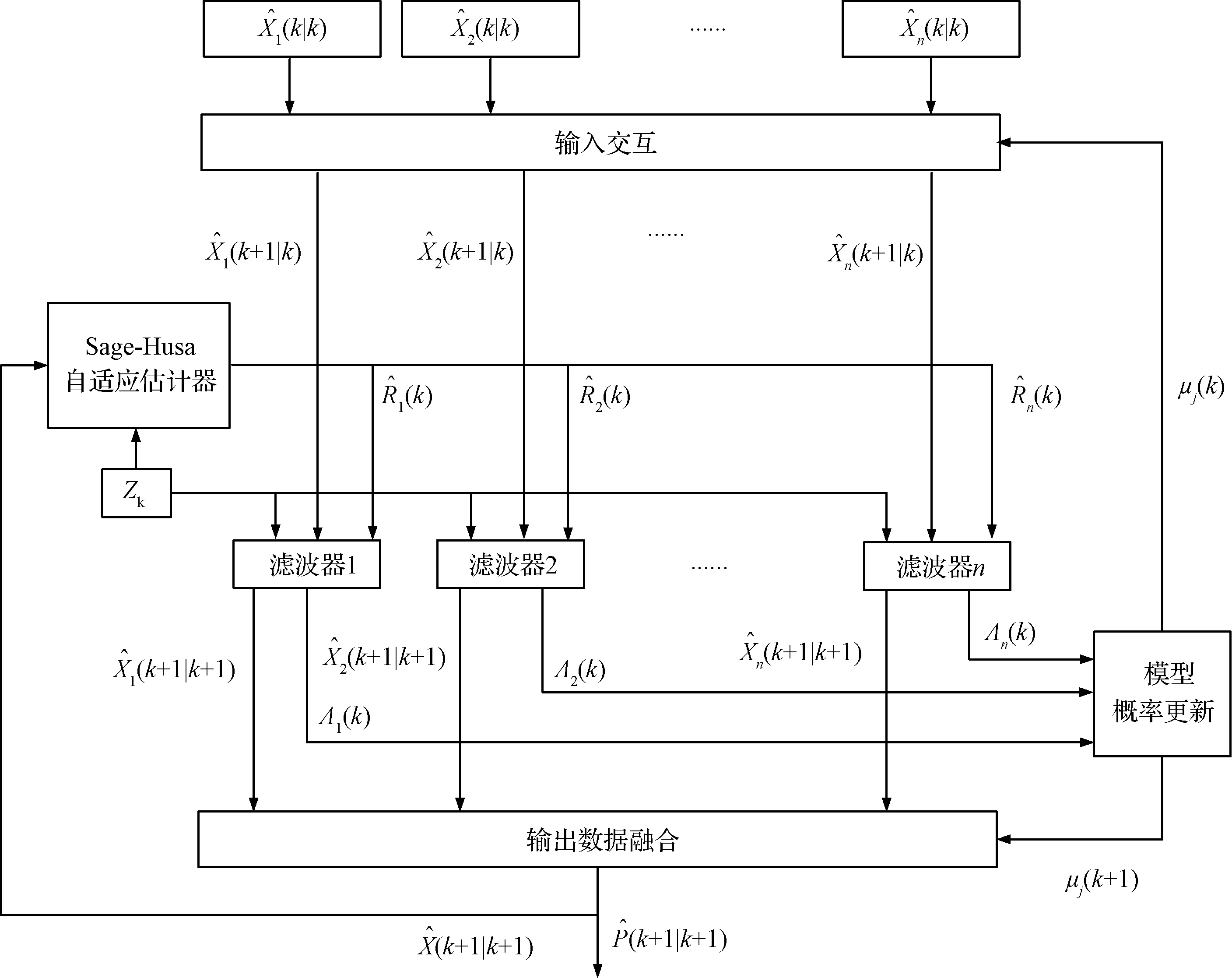
图3 AIMM-UKF算法原理框图Fig.3 Principle block diagram of AIMM-UKF
结合AIMM算法及导航系统状态模型集合的设计,下面给出AIMM-UKF算法的具体过程。
1)输入交互
首先对各个子模型进行初始化并做交互运算,将前一时刻探测器系统状态的交互运算结果作为各个子滤波器的输入,此时导航系统状态的估计值和协方差阵为:
(14)
(15)
式中:μji(k+1|k)是预测模型转移概率:
(16)
2)滤波估计
(17)
(18)
同时,结合自适应参数估计,可得:
(19)
滤波增益为:
(20)
更新各个子滤波器的系统状态及其协方差阵:
(21)
Rj(k)](Kj(k))T
(22)
3)模型更新
结合上述步骤,计算不同子滤波器的新息及其对应协方差阵,并同时更新μji(k+1|k)。
各个子滤波器的新息及其协方差阵如下:
(23)
(24)
更新模型概率时,在k时刻与第j模型匹配的似然函数为:
(25)
(26)
上式中的C为归一化常数,表达式为:
(27)
4)融合输出
以更新后的模型概率μji(k+1)作为各个子模型与探测器真实运动状态逼近程度的指标,对当前各个子模型的输出进行加权融合,得到的结果作为导航系统最终的输出:
(28)
(29)
3 仿真分析
3.1 仿真条件及参数选取
本文仿真所需要的基本参数归结如下。
1)以J2000日心黄道惯性坐标系为参考基准,选取热点探测目标谷神星作为小行星探测工程任务背景开展数学仿真分析,检验本文所提出的一种小推力变轨的天文测角测速组合自主导航方法的有效性。仿真中的真实轨道数据由STK产生,组合导航系统轨道动力学模型包括太阳引力摄动、光压摄动及探测器长期持续的电推力等影响。谷神星等天体的参数通过DE406星历库获得。小行星探测器的相关参数如表1所示。
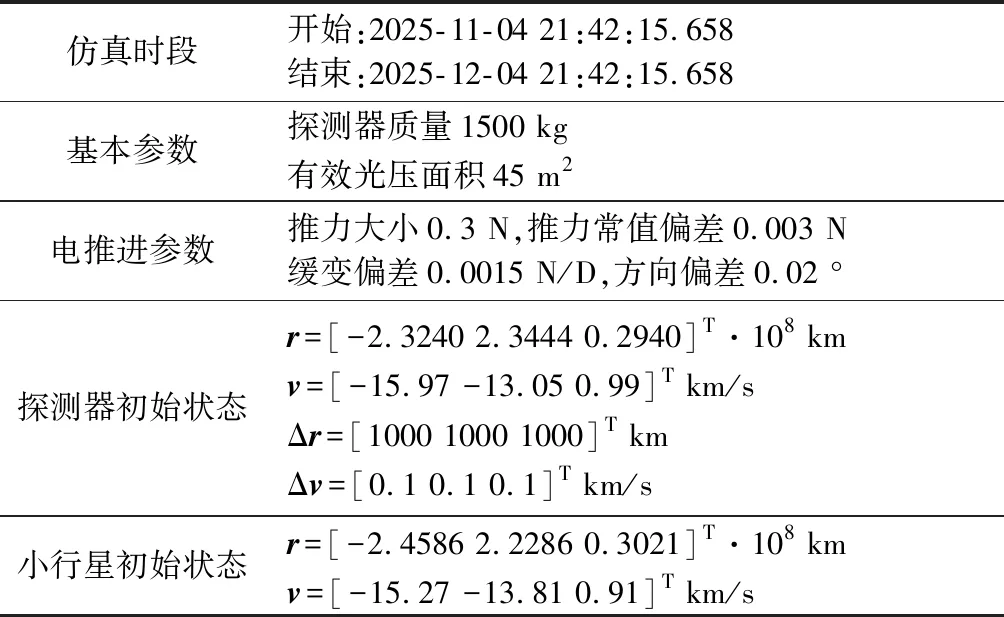
表1 小行星探测器巡航段参数Table 1 Parameters of asteroid probe cruising period
2)测速导航方案中的2颗恒星数据通过依巴谷星表获得,对应的编号分别为35468和60178,相应的星历数据及误差如表2所示。
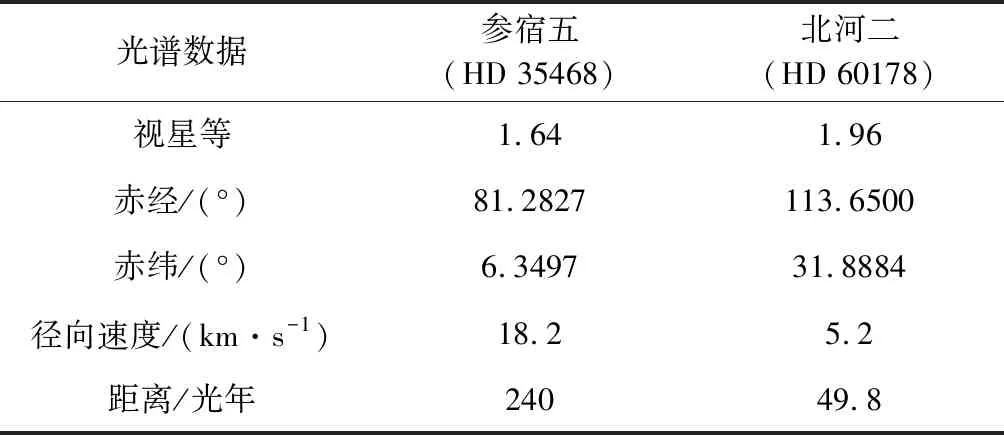
表2 测速导航恒星参数Table 2 Parameters of stars for velocity navigation
3)视线方向矢量量测中测角精度为1″(3σ),太阳光谱测速仪测速精度为1 m/s (3σ),恒星光谱测速仪测速精度为2 m/s (3σ)。
4)相关滤波算法的基本参数设置如表3所示。
5)组合导航系统在交互式多模型中选取4个子模型,模型参数设置如下:
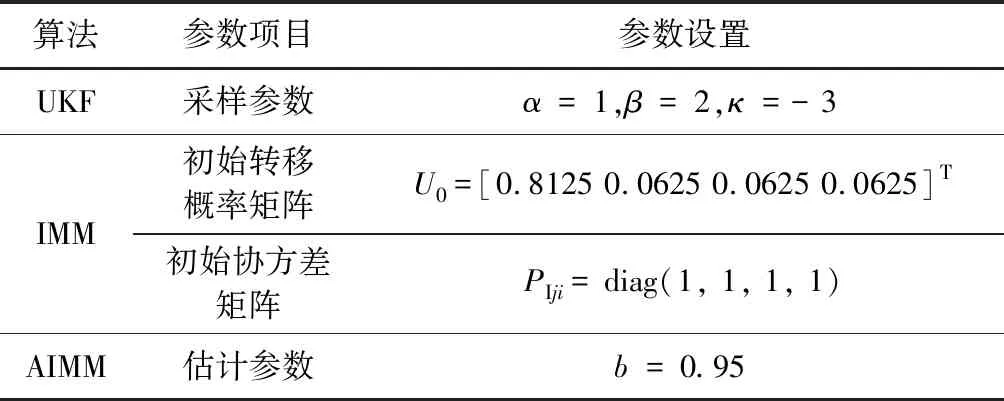
表3 滤波算法参数设置Table 3 Parameters of filtering algorithms
(30)
(31)
多模型集合设置如下:
模型1:Q1=0.01Q;R1=100R。
模型2:Q1=100Q;R1=100R。
模型3:Q1=0.01Q;R1=0.01R。
模型4:Q1=100Q;R1=0.01R。
本文对不同滤波算法采用Monte Carlo方法进行仿真,那么每次滤波估计的均方根误差可以记为:
(32)
在完整的时间序列下,均方根误差可以如下描述:
ψ=[ψ1,ψ2,…,ψn]T
(33)
为了更准确衡量导航滤波算法的精度,在滤波估计收敛后,选取滤波过程末期的L个点的ψ的均值作为整个导航滤波算法的精度指标(3σ),即:
(34)
通常算法的复杂度是判断该算法是否可用于实时处理的依据,在实时性要求高的自主导航系统中作为一项参考指标。算法的复杂度是指其自身在计算中所需的乘法次数,其中不含动力学、量测等产生的时间。在硬件相同时,可采用每次运行的总时间作为滤波算法复杂度的直观度量。
3.2 仿真结果及分析
基于AIMM-UKF算法的测角测速组合自主导航位置与速度估计结果如图4和图5所示,从图中可以看出,组合导航估计很快收敛。
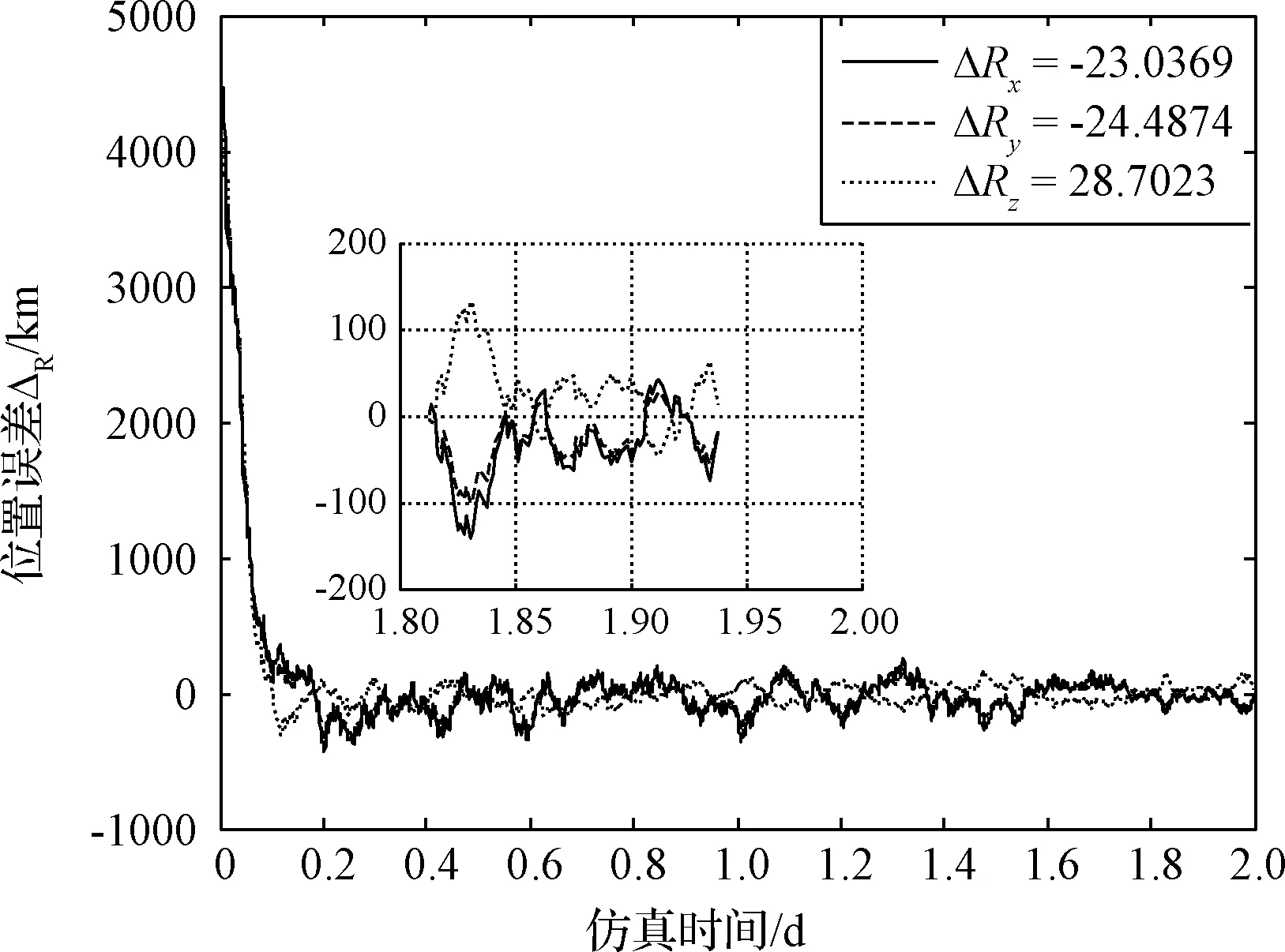
图4 AIMM-UKF算法三轴位置估计结果Fig.4 Three axis position estimation results of AIMM-UKF
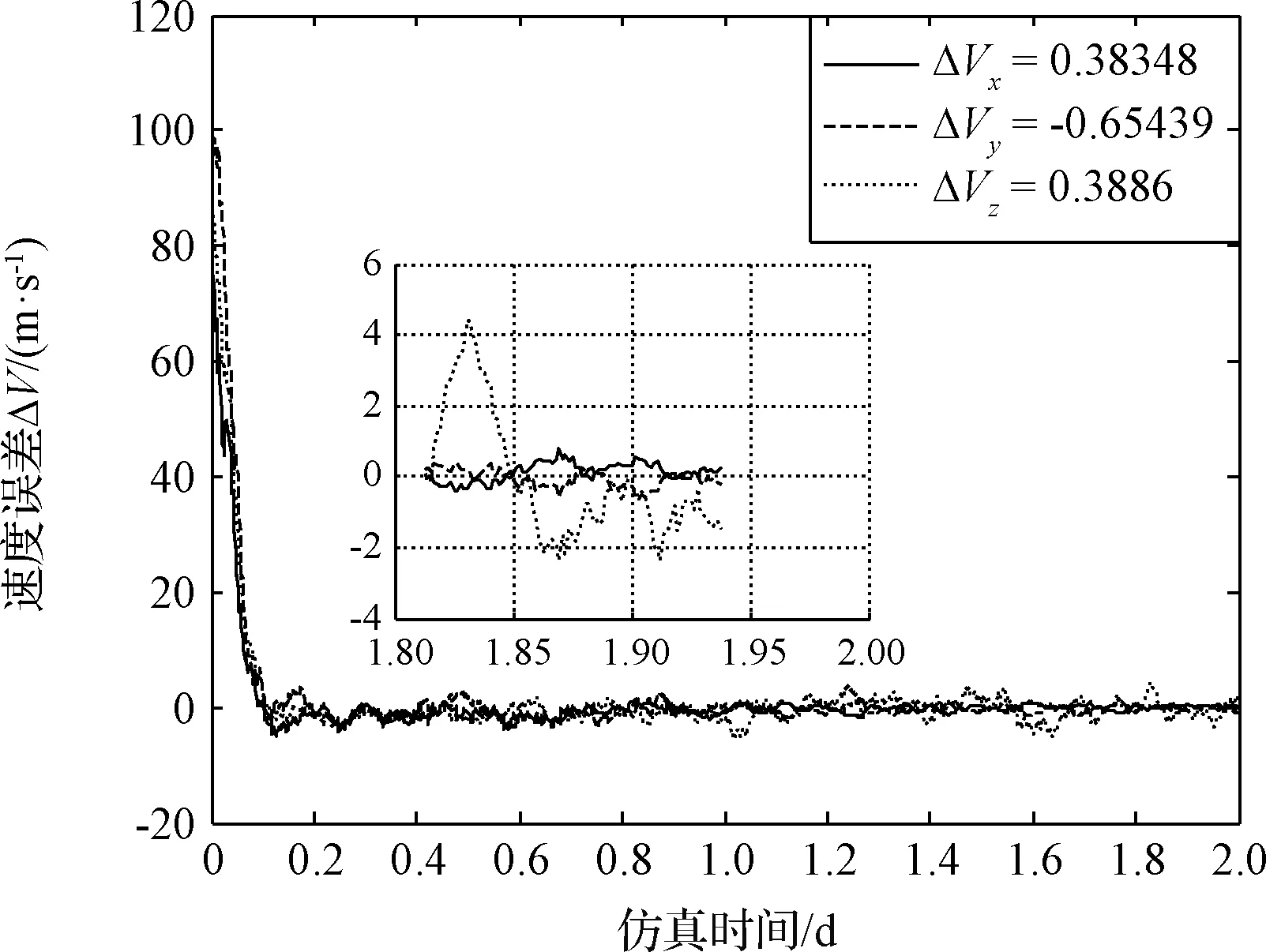
图5 AIMM-UKF算法三轴速度估计结果Fig.5 Three axis velocity estimation results of AIMM-UKF
在仿真算例中,AIMM-UKF采用了4个不同的模型,随着导航滤波逐步递推,AIMM-UKF算法对模型权值不断更新调整。在外部动力学环境不确定情况下,本文所给出的AIMM-UKF算法模型转移概率很快收敛稳定,算法可以很快地匹配到近真实的系统模型,即算法具有很高的自适应性。
为了对比所给出的AIMM-UKF算法性能,下面分别从导航估计结果的精度、计算效率指标上,对比分析AIMM-UKF算法和普通UKF算法、IMM-UKF算法的性能,如图6和图7所示。
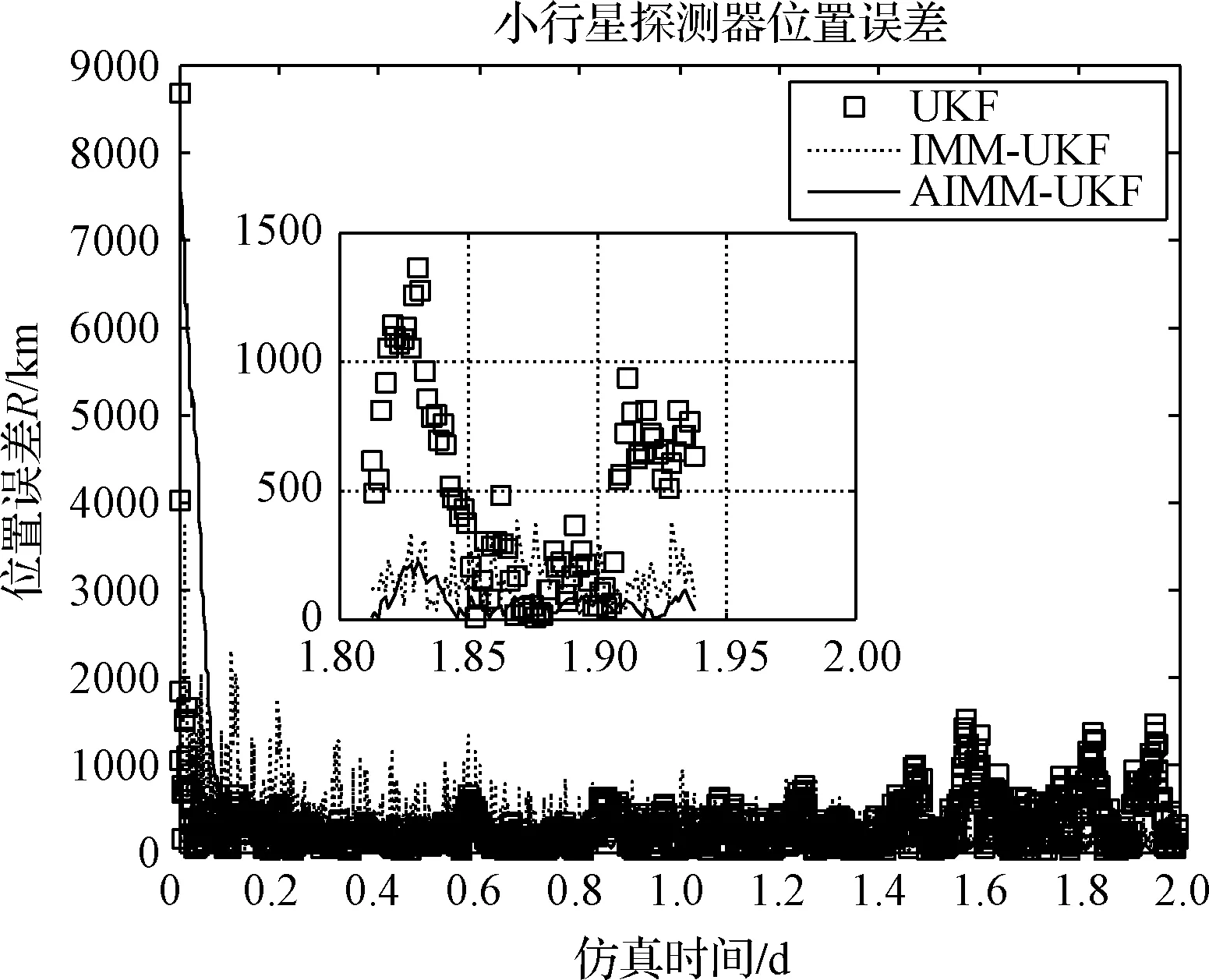
图6 不同导航滤波算法的位置估计结果Fig.6 Position estimation results of different filtering algorithms
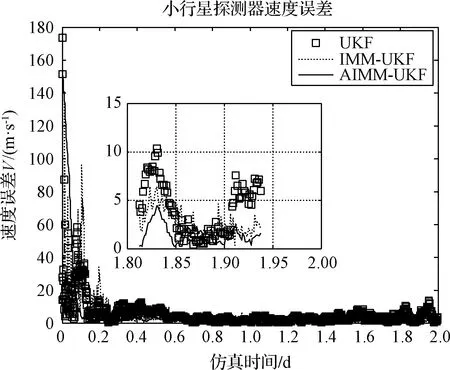
图7 不同导航滤波算法的速度估计结果Fig.7 Velocity estimation results of different filtering algorithms
从上述不同导航滤波算法的估计结果可知,在导航滤波估计的初期,AIMM-UKF算法由于受到初始协方差矩阵权重分配、初始概率分布等因素与实际状态不匹配的影响,滤波估计会有较大超调情况,但随着滤波过程中多模型概率分布的更新,AIMM-UKF算法能够更好地逼近真实的动力学模型和量测模型,它会比普通的UKF和IMM-UKF更快地收敛到稳态,最终AIMM-UKF算法的位置和速度估计精度也会更高。
不同导航滤波算法的估计结果如表4所示。分析可知,普通UKF算法由于模型偏差较大,在导航估计后期逐渐震荡发散;IMM-UKF算法导航估计结果较好;本文所给出的AIMM-UKF算法的位置和速度估计精度比IMM-UKF算法的位置估计精度和速度估计精度分别提升了30.76%和40.55%。
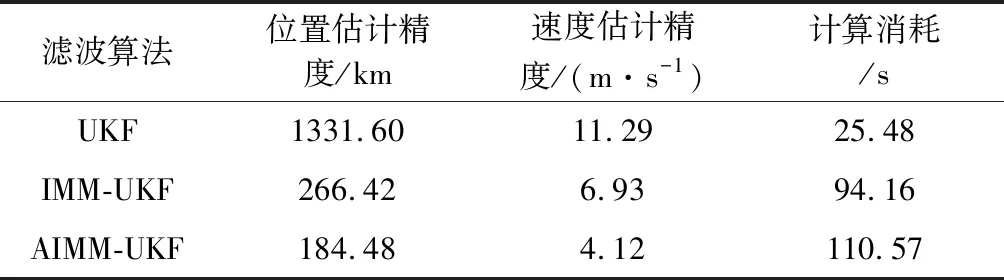
表4 不同导航滤波算法的性能对比Table 4 Performance comparison of different navigation filtering algorithms
4 结 论
针对电推进形式持续小推力变轨的小行星探测任务对导航系统自主性强、实时性高的需求,根据工程实践分析并建立了电推进变轨过程中的动力学模型,给出了天文光学图像测角融合天文光谱测速的小行星探测组合导航方法。为克服小行星探测器推力的不确定性,提出了采用自适应交互式多模型无迹卡尔曼滤波(AIMM-UKF)算法,以较少的模型个数实现对导航系统状态的覆盖,克服了模型集合先验信息不准确对导航精度的影响,提高了组合导航系统的鲁棒性和抗干扰能力。最后,通过基于小行星探测工程任务巡航段的仿真分析,对测角测速组合导航系统的性能进行了对比验证,结果表明本文所提出的组合导航方法估计精度更高、计算消耗更小,可满足小行星探测工程任务对自主导航的高性能需求。
