拓展教学思路 促进深度学习——以一道经典力学题的拓展教学为例

陈志军

(安徽省绩溪中学,安徽 宣城 245300)

深度学习具有促进知识建构、着意迁移运用、面向问题解决的基本特征和思维层次，追求有效的学习迁移和真实问题的解决.[1]深度学习是落实物理学科核心素养的重要途径，引导学生积极参与、体验探究学习过程，掌握学科的核心知识，把握学科的本质及思想方法.[2]应用迁移、拓展探究则是构建思维型课堂的基本方法，是深度教学的主要特征，教学过程突出知识的形成过程、思维品质的训练，着重发展学生高阶思维和实际问题解决能力.[1]本文以一道经典力学题的拓展教学为例，着眼于知识的迁移应用和思维的发散，着力解决实际问题，促进学生深度学习，落实物理核心素养教学目标.

1 一道经典力学题

图1

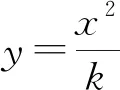
2 拓展探究教学分析

2.1 弯杆上任意点的斜率

(1) 利用极限法.

(2) 利用微分思想.

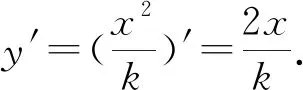
(3) 利用平抛运动的规律.

图2

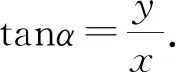
2.2 环的运动性质与规律

(1) 环在何处相对杆静止.

(2) 环运动的性质和模型分析.

图3

环运动的性质是水平面内的匀速圆周运动，所受重力和支持力提供向心力.教学中设计探究活动深入分析，将支持力方向延长交y轴于A点，探究确定环的运动符合“无绳”圆锥摆运动模型，如图3所示，A点为圆锥摆的悬挂点，摆角为θ，AP为摆线，其轨迹在水平面内的一种典型的匀速圆周运动.题目并没有给出摆角，要引导学生探究摆角的确定方法并求曲线的斜率，学生讨论，教师指导，共同分析、评价、探讨.圆锥摆运动模型是一种典型的力学模型，涉及到运动、力、能量等物理观念.而日常生活中经常会遇到一些圆周运动，本质是圆锥摆，只是少了摆线，教学中引导学生通过与实际生活联系，探究发现这些“无绳”的圆锥摆，分析该状态下物体受力的特点、运动的规律，能很好地培养学生科学探究能力、科学思维能力、科学态度与责任和解决实际问题的能力，形成和发展物理观念，指向物理学科核心素养的培养.[3]

(3) 逆向探究弯杆的曲线方程.

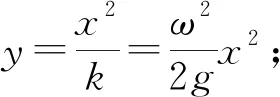
(4) 不同转速下的弯杆约束的运动.

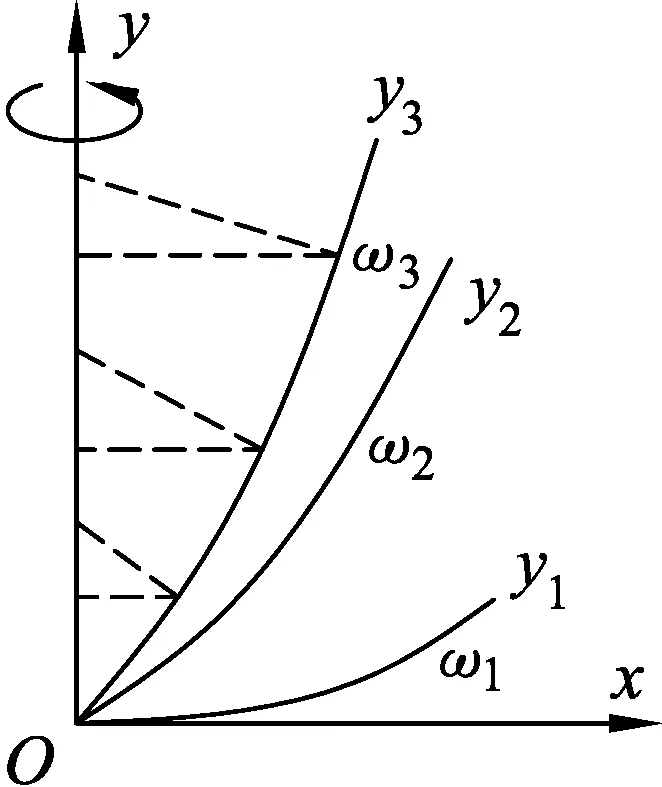
图4

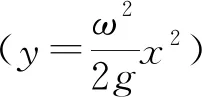
2.3 引入非惯性系，确定相对静止的位置

图5

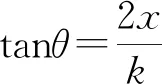
2.4 与直杆约束的圆周运动对比分析

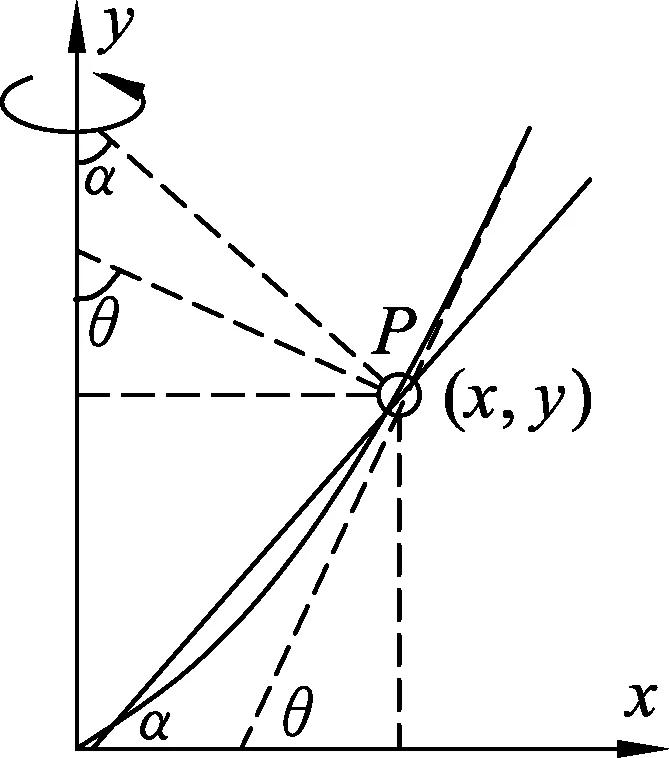
图6

2.5 与圆形轨道约束的圆周运动对比分析

图7

如图7所示，光滑圆形杆的半径为R，环可以随圆形杆一起匀速转动.根据圆的性质和坐标系中的位置，可以确定该圆的轨迹方程为x2+(y-R)2=R2.假设环在坐标为(x0，y0)的任意位置P点处以角速度ω0随圆形杆一起做水平面内的匀速圆周运动，很明显该运动在本质上仍然是圆锥摆运动.该点的切线对应的角度θ即为摆角，利用微分求导可以确定该点切线的斜率为

(1)

又根据环做匀速圆周运动的动力学方程知

mgtanθ=mω02x0=mω02·Rsinθ.

(2)

联立(1)、(2)式可解得

(3)

(4)

(5)

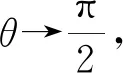
从上述分析可以看出，直杆、特定形状的抛物线杆、圆形杆都可以带动圆环做“无绳”圆锥摆运动，直杆的情况下环的位置和角速度有一一对应关系；环可以随特定形状的抛物线杆在任意位置做水平面内的匀速圆周运动；而圆形杆的角速度必须要超过一个临界值，才能使环运动起来.

3 结语

本题模型涉及物理学科核心素养，促进深度学习的探究点比较多.教学中要针对性拓展探究曲线切线斜率、支持力的大小及方向、圆锥摆的特征物理量、任意角速度对应的曲线方程、非惯性系中受力分析和切向加速度分析、与直杆以及圆形轨道约束的圆周运动对比分析.

学生在教师的引导下积极参与科学探究活动，主动获取知识、发展探究能力.在解决实际问题的探究中深入理解原有的认知结构，构建新的物理知识结构体系，克服学生知识的分散和不系统等弊端；拓展探究为学生提供交流展示的平台，收获探究的乐趣与成功的喜悦，增强物理学习的兴趣与信心；学生在合作、交流与评价中发现和反思自己的不足，培养学生的合作探究意识，有助于培养学生的发散思维和创新能力，克服认识的表面性、肤浅性，达到深度学习的目的，落实物理学科核心素养的教学目标.