篮球真有可能向上运动吗？——评2020年北京高考物理第14题

邓靖武

(北京教育学院数学与科学教育学院,北京 100120)

2020年北京高考物理试题注重联系生活实际情境创设. 试题其中选择题最后一题(第14题)为旋转的篮球在空气中运动的情况，笔者针对该题的情境进行了相应的分析，与同行探讨.

1 试题再现及分析

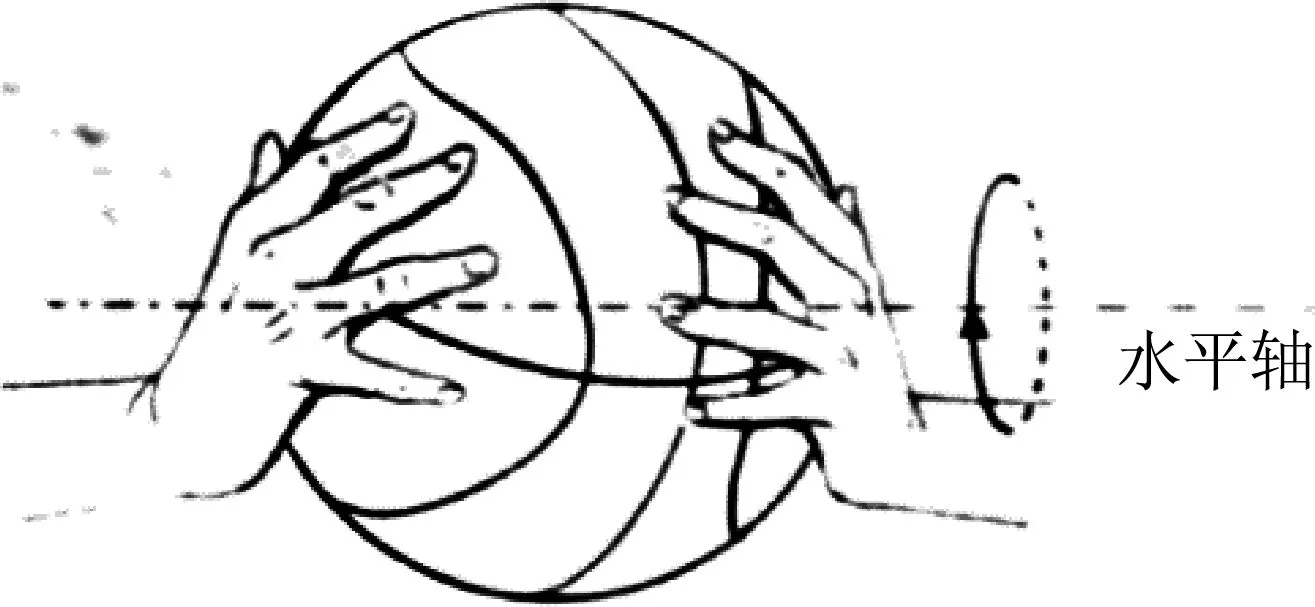
图1 绕水平轴旋转的篮球

例题.在无风的环境,某人在高处释放静止的篮球,篮球竖直下落;如果先让篮球以一定的角速度绕过球心的水平轴转动(如图1所示)再释放,则篮球在向下掉落的过程中偏离竖直方向做曲线运动. 其原因是,转动的篮球在运动过程中除受重力外,还受到空气施加的阻力f1和偏转力f2. 这两个力与篮球速度v的关系大致为f1=k1v2,方向与篮球运动方向相反;f2=k2v,方向与篮球运动方向垂直. 下列说法正确的是

(A)k1、k2是与篮球转动角速度无关的常量.

(B) 篮球可回到原高度且角速度与释放时的角速度相同.

(C) 人站得足够高,落地前篮球有可能向上运动.

(D) 释放条件合适,篮球有可能在空中持续一段水平直线运动.

解析:该题有效考查了学生的迁移运用能力,即要求学生运用所学知识进行综合分析判断,解决问题.学生根据题干中给定的信息:篮球未转动的情况下竖直下落,转动的情况下由于受偏转力的作用做曲线运动,容易排除(A)选项;通过机械能守恒定律也容易判断(B)选项错误;通过假设篮球可以水平运动,进而判断由于阻力作用会使篮球速度减小,从而导致受到的竖直向上的偏转力减小,无法与重力等大反向,从而判断(D)选项错误.最终可以通过排除法选择(C)答案.但是(C)答案中描述的人站得足够高,篮球落地前有可能向上运动,真是如此吗?

2 球体在流体中的运动

2.1 流体阻力

流体介质对在其中运动的物体阻力大小与速度有关,阻力包括粘滞阻力和压差阻力两部分,其规律一般可以表示为[1]f(v)=γv+kv2.其中第1项为粘滞阻力,即物体浸在黏滞流体中运动时,物体表面附近的流层间就存在一定的速度梯度.物体所受的黏滞阻力就是物体表面附近的流层间的内摩擦力引起的.第2项为压差阻力,它是由于运动的物体前后所形成的压强差所形成的,与物体的迎风面积、形状和气流中的位置有关系.当速度较小时,黏滞阻力大于压差阻力,当速度较大时,压差阻力大于黏滞阻力.

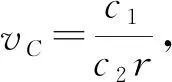
考虑本试题中的篮球,通常成人使用的7号篮球(标准球)质量为600～650 g,周长为750～760 mm,若取篮球半径为r=0.12 m,则篮球在空气中运动黏滞阻力与压差阻力相等的临界速度vC=3.0×10-3m/s. 该临界速度与篮球实际运动速度相比非常小,因此,篮球在空气中下落主要受到的是压差阻力. 由于空气阻力的存在,那么篮球在空气中自由运动的最大速度是多少呢?

2.2 收尾速度

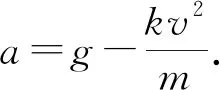
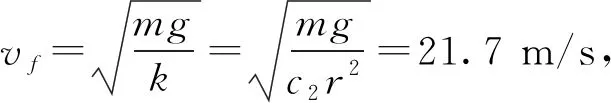
2.3 马格努斯效应

图2 马格努斯效应装置

当圆柱体绕自身轴线旋转并且有流体在垂直于该轴线方向流过时,它会受到一个垂直于流动方向的横向力,力的方向总是从来流方向与圆柱面上线速度是相反的那一边指向相同的另一边.这种现象被称为马格努斯效应.[2]它是1852年由马格努斯(Magnus)发现的,研究马格努斯效应的最初原因是因为球面形的子弹经常会受到绕横轴的意外转动而造成飞行轨迹偏向一边.[3]他采用的实验装置如图2所示,在两个圆锥形轴承之间安装了一个黄铜圆筒,以绳子带动其旋转. 他安装了吹风机向圆筒上吹风,当吹风机工作时,他发现了横向作用力的存在.[4]“香蕉球”、“弧圈球”中的横向力都是马格努斯效应的结果. 本文讨论的高考试题中篮球在旋转下落的过程中偏离竖直方向同样也是该效应的结果.

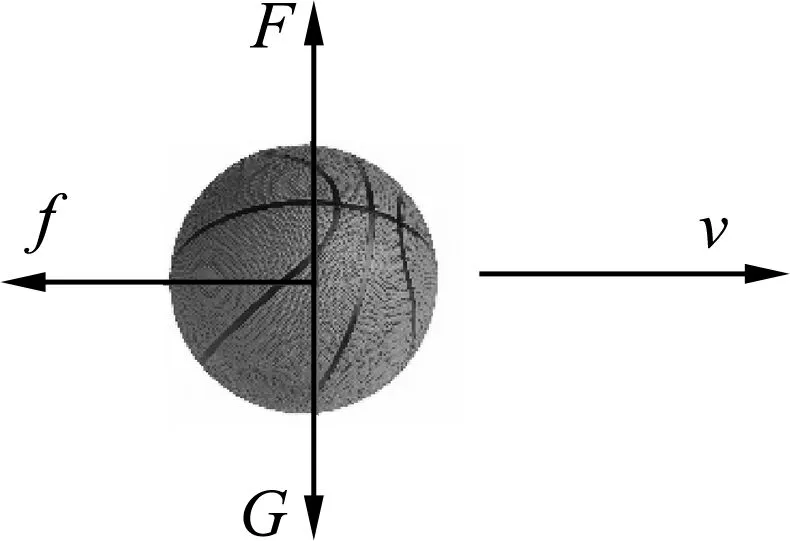
图3 速度水平时篮球受力

基于此模型,我们可以探讨试题中篮球的运动情况.若篮球最终能够向上运动,考虑篮球在运动过程中速度方向变为水平的方向的时刻,如图3所示. 分析篮球所受重力与马格努斯升力的大小关系,若升力大于重力,则篮球将向上运动,否则篮球将向下运动.

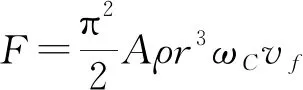
由此可见,假设篮球在水平方向上以收尾速度前进,要让篮球能向上运动,其角速度应该不小于24.7 rad/s.

3 数值模拟及讨论

3.1 分析及数值模拟

通过前面的分析可知,在高度足够高的情况下,篮球要能向上运动,转动的角速度有一个临界值ωC.如果小于这一值,无论多高释放,篮球都不可能向上运动. 而上述计算只是一个估算,估算中至少有几处导致了临界值估算变小:第一是直接使用了理论上的收尾速度作为速度水平方向时刻的运行速度,显然这一点会产生较大差别. 第二是数学模型中系数A取1进行计算(0

为了更为准确地估算临界值,根据上述模型进行了数值模拟,利用前面提到的篮球的参数,分别以初始转动角速度10 rad/s，50 rad/s，60 rad/s,进行数值模拟,其下降高度与水平位移轨迹图如图4所示.

图4 不同角度下篮球轨迹模拟图

从数值模拟结果可以看出,如果释放篮球时,其初始角速度较小,篮球在下落的过程中会由于马格努斯力的作用而导致横向偏移,但不会向上运动.只有当初始角速度达到50 rad/s左右时才会出现向上运动的临界情况. 当以角速度60 rad/s释放篮球时,在下落的过程中会出现一定幅度的向上运动.

3.2 讨论

通过前面的分析与数值模拟,再回到本文前面提到的试题. 由于篮球下落时初始角速度并没有给定,因此要释放高度足够高的情况下,篮球要能向上运动,释放时的初始角速度要超过某一临界值,如果按照数值模拟的结果来看,需要初始角速度大于50 rad/s,即需要大约每秒转动8圈的转速才可能向上运动,而这样的转速,徒手抛出并不容易,因此实际中篮球难以实现运动过程中向上运动,这一点从多个抛球的视频也能得到验证.

当然,这一问题的实际力学过程可能比上述分析与模拟复杂得多,在此通过多种简化和近似估算得出结论,供同行探讨、批评指正.

(本文数值模拟及作图由北京大学物理学院杜卓晨完成)