新型可穿戴上肢康复机构的设计与分析

郭 盛，马 可，王向阳

(北京交通大学 机械与电子控制工程学院，北京 100044)

调查显示，老龄化和高强度工作导致劳动力人口的身体状况不容乐观，相关疾病的偏瘫症状将会造成肢体残疾.康复训练是使此类病人恢复自主运动的主要治疗方式.传统康复训练效率低、强度不足，因此采用机械装置通过主动式上肢康复运动训练，对于增进上肢偏瘫患者的肌肉活性及促进感知等方面，是一种理想的解决手段.

目前上肢康复器械种类较多，针对不同上肢关节康复已有较多研究，如北京交通大学张秀丽设计的一种基于串联弹性驱动器的3自由度柔顺机械臂[1]；常州大学沈慧平等设计的一款具备单输入三转动输出特性的并联式可穿戴肩关节康复训练机器人[2]；美国Myomo公司推出的肘关节1个自由度穿戴式脑卒中康复机器人MPower1000[3].上述机构都只适用于局部关节康复，不适用于整只手臂瘫痪患者的全面康复.长安大学研制出一款可穿戴外骨骼式上肢康复训练机器人[4]，具有3个自由度，但该机器人采用串联结构，虽然工作空间较大，但结构刚度低、控制误差较大.南京理工大学研制出的一款可穿戴外骨骼式4自由度上肢康复机器[5]，可满足肩部及手肘的康复需求，但以上机构大多是刚性体以及刚性驱动，使得患者的使用舒适度下降.美国的David Mayhew等研制出的MACARM[6]上肢康复机器人及意大利Giulio Rosati等研制出的NeReBot[7]、MariBot[8]5自由度上肢康复机器人均属于绳驱动非穿戴式机器人，虽然结构简单，但所需驱动数大于机构自由度数，造成额外系统质量.其他如意大利的Tobias Nef等研制的ARMin[9]上肢康复训练机器人，以及美国华盛顿大学Joel C. Perry等研发的CADEN-7[10]外骨骼机器人，均为非穿戴式上肢设备，机构庞大，康复地点固定，不具备轻便性.

本文作者面向上肢运动障碍患者，改善现存上肢康复机构结构设计的不足，采用串并混联式结构，以满足患者日常康复需求为目标，设计了一种结合柔性材料的混联上肢可穿戴康复训练机器人，并对其运动学、运动静力学进行了分析，通过仿真验证其作为人体上肢康复机构本体的可行性.

1 结构设计

上肢主要由肩关节、肘关节、前臂和手部连接.共具有7个运动自由度.肩关节简化为1个球窝关节，具有屈/伸、外展/内收、旋内/旋外3个自由度；肘关节简化为1个铰关节，具有1个屈/伸自由度；前臂具有旋内/旋外1个自由度；腕关节提供屈/伸、外展/内收、旋内/旋外2个自由度.我国成年人人体尺寸标准如表1所示.

表1 人体上肢结构尺寸

结合人体躯干平均尺寸参数，并依此设计如图1所示的康复训练机构.该机构包括肩部机构、肘部机构、及手腕机构三大部分.

肩部机构为3-UPS/S并联机构，由肩部固定基座、3条完全相同的UPS支链组成，具有空间3个转动自由度.每条运动支链由万向节、气缸及球铰构成.穿戴时，患者肢体肩关节可视为球铰，通过定长杆(上臂)与肘部平台(图示动平台1)固接.整体形成3-UPS/S并联结构.因此，肘部平台由于机械约束只能实现以肩关节为转动中心的空间三维转动.肘部平台姿态可由3条支链气缸驱动进行调节，实现大臂3个自由度的转动.

肘部机构为平面四杆机构，可实现肘部1个转动自由度.动平台1与动平台2铰接，并通过气缸驱动伸缩，实现肘关节屈伸运动.调节连杆用于适应不同患者前臂尺寸，以提高穿戴舒适度.

前臂及手腕机构为编织手套，采用人造肌肉驱动.基于燕大柔性可穿戴手套[11]，改进人造肌肉配置方式使之适用于患者手掌的多自由度不规则运动形式.手腕部分使用收缩人造肌肉，当充气施加压力，收缩人造肌肉缩短提供拉力.人造肌肉2充气缩短，人造肌肉3放气伸长实现手腕内收；人造肌肉3充气缩短，人造肌肉2放气伸长完成手腕外展运动；同理，手腕屈伸运动由相拮抗的人造肌肉4和人造肌肉1实现.手腕环转自由度由弯曲人造肌肉控制，以人工伸肌为材料，肌肉通过增加施加压力弯曲，弯曲角度随施加压力的增加而增加.

2 机构刚体部分运动学分析

2.1 肩部机构运动学

建立如图2所示肩部机构运动学模型.图中，并联机构转动副分布在以肩关节O1为圆心，半径为h的周边圆上.动平台1的圆心为O2，半径为r，Ai为U型副中心，Bi为球铰中心.以O1为原点建立全局基础坐标系O1-x1y1z1，x1指向A1.以O2为原点建立基础坐标系O2-x2y2z2，x2轴指向B1.肩部3个气缸的长度为li(i=1，2，3)，人体上臂O1O2长为s，动平台相对于定平台的一般姿态变换矩阵为

RT=Rot(z,γ)·Rot(y,β)·Rot(x,α)

(1)

已知在O1-x1y1z1坐标系中Ai的坐标和O2-x2y2z2坐标系中Bi的坐标，则O1Bi在全局坐标系中可表示为

O1Bi=O1O2+RT·O2Bi′

(2)

可得

(3)

对于单一支链，其矢量闭环示意图如图3所示.

建立矢量闭环方程为

O1O2+O2Bi=O1Ai+AiBi

(4)

矢量方程式(4)对时间进行求导得

(5)

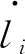
式(5)两端叉乘wi得到支链角速度为

(6)

式中JJ为一个3×3矩阵，即

JJ=

(7)

Ki为一个3×4矩阵，即

(8)

式(5)两端点乘wi得到伸缩运动速度为

(9)

2.2 肘部机构运动学

建立如图4所示肘部机构运动学模型.该模型建立在肩部机构动平台的基础上，转动副C1、C2、C3分布在延z2向上平移距离p所得的圆周O3上，以O3为原点建立基础坐标系O3-x3y3z3，x3轴指向C1，该坐标系与O2-x2y2z2同向.动平台2圆心为O4，半径为k.肘部气缸长度为l4，小臂O3O4长为n.该机构可简化为RPRR平面四杆机构模型(图5)，其中C2、C3共转动轴线.

根据手肘部分几何关系，可得l4与θ的关系为

l4=

(10)

计算肘部气缸速度.肘部支链示意见图5.

与肩部速度求解同理.O2-x2y2z2坐标系下肘部角速度ω4为

(11)

式中：ωb为动平台2相对动平台1的角速度；Jz为雅克比矩阵

Jz=

(12)

w4为O2-x2y2z2坐标下l4上的单位向量

(13)

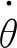
RT′·vs

(14)

式中RT′为一个3×4矩阵，即

(15)

全局坐标下动平台2角速度ωb′为

(16)

式中:RT″为一个3×4矩阵，即

(17)

全局坐标下肘部角速度w4′为

w4′=RT·w4

(18)

(19)

2.3 工作空间范围及奇异特性

由式(9)可知，肩部雅可比矩阵为

(20)

由肩部雅可比矩阵行列式[Ja]=0，得到h=0或r=0或α、β、γ3个角度之间关系式为

(21)

其中：a1=2sinα·(s-rsinβ)·

(r-rcosα·cosβ+2s·sinβ)

a2=-2cosα·(s-rsinβ)·(2s+rsinβ)+

cosβ·(r2-4s2-r2cos(2α)+

rs(-3+cos(2α))·sinβ)

此时肩部处于奇异位置.由式(19)可知，肘部雅可比矩阵为

[Jb]=[O3D1×w4]

(22)

由肘部雅可比矩阵行列式det[Jb]=0，得到角度θ=-90°或θ=90°.此时肘部处于奇异位置.

由机构仿真运动到边界得到康复机构运动边界范围.表2为人体上肢关节活动范围与康复机构运动边界范围.

表2 人体上肢关节活动范围与康复机构运动边界范围

由表2可知，除肩关节伸运动、内收运动及肘关节伸运动外，人体上肢关节活动范围基本包括在康复机构运动边界范围之内.且此上肢康复机构运动边界范围满足偏瘫患者上肢七级评估分级表康复规定动作.

3 机构运动静力学分析

运动静力学分析基于虚功原理，其将运动过程的每一时刻通过静力学建模，建立惯性力、驱动力和其余外力的静平衡关系.由于此机构在承载人体上肢重力的情况下，缓慢按照预定轨迹进行康复运动，因此在建模过程中，可忽视加速度项引起的惯性力变化.

3.1 运动静力学建模概述

为获取机构受力关系，建立如图6所示的气缸模型[12].以肩部气缸为例.气缸由质量为m1的缸体和质量为m2的活塞组成.e1是Ai和第i(i=1,2,3)条支链缸体质心距离，e2是Bi与第i(i=1,2,3)条支链中活塞质心距离.

3.2 肘部运动静力学

考虑肘部装置、人体前臂以及手腕装置重量，设力臂作用在手臂的质心，动平台2部分只受重力，力臂项为零.建立如图7所示肘部模型.

与肩部气缸模型一样：肘部e3是C1与圆筒质心距离，质量m3；e4是D1与活塞质心的距离，质量m4.动平台2的质量为m0′，mn为前臂质心质量，mt为前臂两端长度调节杆件质量.

(23)

其中

(24)

(25)

其中

(26)

动平台2速度项v2为

(27)

其中

[J2]=

(28)

O3O4=[-ncosθ(cosγsinβcosα+sinγsinα) 0

nsinθcosβcosα]T

(29)

人体前臂速度项v3为

(30)

其中

(31)

(32)

(33)

动平台2质心受力项F2为

(34)

人体前臂受力项F3为

(35)

式中M2=[M2xM2yM2z]为肘部自主施加力矩.

根据虚功原理可得

[J2]T·F2+[J3]T·F3=0

(36)

结果为4×1方程组，代表各广义速度方向的合力为0，处于平衡状态.由此可以计算得出任意静止状态手肘部分气缸所需力f4及此刻f1、f2、f3大小.

3.3 肩部运动静力学

肩部承受康复装置整体重量以及人体手臂重量，包含肩部机构框架、上臂质量、前臂质量、手腕部动平台及肘部气缸装置质量(装置及前臂质心可简化到一点).在全局坐标系下，建立如图8所示的肩部运动静力学模型.图中ms为人体上臂质量.

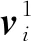
(37)

(38)

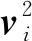
(39)

其中

(40)

动平台1速度项v1为

(41)

其中

(42)

O1O2=[s(cosγsinβcosα+sinγsinα)s(sinγsinβcosα-sinαcosγ)scosβcosα]T

(43)

上臂速度项v4为

(44)

其中

[J4]=

(45)

由于在康复训练过程中人体肘部处于放松随动状态，可得M2=03×1.

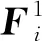
(46)

(47)

动平台1质心受力项F1为

(48)

上臂质心受力项F4为

(49)

式中：M1=[M1xM1yM1z]为肩部自主施加力矩.

根据虚功原理可以得到

(50)

结果为一个4×1方程组，代表各广义速度方向的合力为0，处于平衡状态.由此可以计算得出此时f1、f2、f3以及对应肘部气缸f4的驱动力大小.

4 典型康复运动实现及仿真验证

患者进行康复训练的最终目的为恢复上肢日常活动，以康复中的提臂运动为例.

成年男性前臂重量约1.5 kg，长度约220 mm；上肢重量约3.5 kg，长度约为290 mm、手掌重量约0.3 kg.自主施加力矩M1=[0 50 0]、M2=03×1.各参数h=65 mm、r=50 mm、k=40 mm、e1=60 mm、e2=75 mm、e3=50 mm、e4=65 mm.基座、动平台1、动平台2采用PC塑料，气缸及调节连杆材料为铝合金.导入仿真软件.仿真界面如图9所示.

在人体上肢活动范围内，给定广义坐标位置与时间关系方程为

(51)

式中：α(t)、β(t)、γ(t)、θ(t)单位为deg.

开始与结束姿态如图10所示.通过机构运动学逆解，由目标轨迹方程求解出各个驱动在给任务期间的变化曲线.如图11所示，分别为ADAMS数值仿真分析和理论解算所得的逆解结果，各杆长变化在时间段0～5 s内的变化由于虚拟样机装配误差，幅度和趋势有少许误差，在合理范围之内，验证了前述运动学建模的正确性.同时，如图12所示，通过虚功原理对运动静力进行解算，得出4个驱动力随时间的变化曲线.与仿真结果进行对比，两者曲线的走势在1 s后趋于一致，在1 s前仿真具有明显的波动.该波动是由于仿真初始位置不在目标轨迹上，造成仿真器初始位置“瞬移”产生了较大加速度.驱动力曲线仿真数值始终比驱动力曲线理论数值大，该差值是由于虚拟仿真存在加速度，会产生一定惯性力，惯性力大小由部件质量与此刻加速度大小决定.通过以上分析，验证了运动静力学建模的正确性，并为气缸的选型提供了理论依据.

5 结论

1)设计了一种新型可穿戴柔性上肢康复训练机构，利用混联结构及柔性手套对比传统刚性、串联、绳驱动结构，在满足康复训练所需运动自由度同时，肩部承载力更大，结构更紧凑，前臂及手腕部更轻便.

2)对机构刚性部分进行运动学建模，解算运动学逆解，并通过虚功原理建立机构运动静力学模型，得到特定上肢动作的运动学及运动静力学理论解.

3)将康复外骨骼运动路径导入ADAMS进行仿真，得到对应运动学和运动静力学仿真分析结果.与理论计算结果进行对比，验证了模型及分析的正确性，为后续研究奠定了基础.