基于奇异向量鲁棒性的水印方法的质量补偿分析*

王文冰，刘胜利

(1.战略支援部队信息工程大学网络空间安全学院，河南 郑州 450001; 2.郑州轻工业大学软件学院，河南 郑州 450000)

1 引言

网络开放环境使多媒体信息访问更加便利，但同时带来了内容认证、版权保护等新课题。数字水印作为多媒体保护手段之一，以其隐蔽、操作简单等特点持续吸引学者关注。其中，鲁棒水印指在载体中嵌入称为水印的信息，当图像经受各种攻击之后，水印仍能被基本完好地提取出来，以认证载体图像的所有权。

水印有4个基本特点：不可见性、鲁棒性、安全性与可证明性，根据嵌入域不同可分为空域水印与频域水印。空域水印直接修改空域像素嵌入水印，计算复杂度低，但图像处理对像素的干扰降低了鲁棒性[1]。基于频域的水印方法利用频域变换的能量聚集、多重解析等优点，具备更高的鲁棒性与图像质量。基于频域的鲁棒水印方法常利用奇异值分解SVD(Singular Value Decomposition)中奇异值的稳定性、不包含图像结构信息等特点嵌入水印[2]。多数基于SVD的鲁棒水印，把水印或水印奇异值与载体奇异值的加权和做正向SVD分解，得到的奇异值替代原有奇异值后，再做反向SVD分解得到水印图像[3 - 6]。Singh等[3]结合冗余离散小波变换RDWT(Redundant Discrete Wavelet Transform)、非下采样轮廓波变换NSCT(NonSubsampled Contourlet Transform)和SVD实现半盲水印，RDWT与NSCT变换使方法具备抵抗常见图像处理的能力，SVD分解与Arnold置乱分别提高水印算法的鲁棒性与安全性。Makbol等[4]在小波域上对图像做SVD分解。Araghi 等[5]同样基于小波域，并对载体做2次SVD分解以嵌入水印。Vali等[6]在优化嵌入强度与签名嵌入时分别使用自适应差分进化技术与基于熵选取签名嵌入块。此类方法嵌入量大、鲁棒性高，但易产生版权证明的二义性，攻击者利用这一点，可以在任意图像中提取出仿造水印以冒充图像所有者[7]。Chung等[8]指出除了奇异值具备鲁棒性外，左右奇异向量的列向量同样具备鲁棒性。在此基础上，Fan等[9]提出左右奇异矩阵的第1列向量具备鲁棒性并给出了理论依据。在文献[9]的基础上，文献[10-17]均通过量化调制奇异矩值第1列元素差值以嵌入水印。Chang等[10]把图像分块并做SVD分解，利用非零奇异值个数排序选取嵌入块，再修改嵌入块的左奇异向量的第1列元素之间的关系以嵌入水印。文献[11,12]利用信息熵选择嵌入块，并在嵌入前对嵌入块做离散余弦变换(DCT)与SVD分解。Ali等[13]在再分布不变离散小波变换RIDWT(Redistributed Invariant Discrete Wavelet Transform)域上利用蜂群优化技术选取嵌入阈值。Makbol等[14]利用离散小波变换(DWT)低频域对图像变化的低敏感性提高方法的鲁棒性。文献[15,16]把修改奇异向量第1列元素之间关系以嵌入水印的方法应用到彩色图像上。Wu等[17]同样是针对彩色图像，区别是先把水印通过DNA(DeoxyriboNucleic Acid)编码与耦合映像格子CML(Coupled Map Lattice)加密后，再嵌入到载体的右奇异向量中。

Fan等[9]第1次提出在基于奇异向量鲁棒性的水印方法中，修改一个奇异向量所引起的质量受损可通过修改另一个奇异向量做补偿，该文献使用让载体相邻元素不变的修改量均值做补偿参数。不同于文献[9]对矩阵做全局质量比较的方式，Su等[15]分别对每个像素的质量补偿效果做评估，从而确定最佳补偿参数。Ali等[13]利用蜂群优化技术选取质量补偿参数。然而，上述算法的质量补偿参数都无法从理论上证明其是最优参数。

不同于其他方法通过反复实验确定补偿参数或估计补偿参数，本文从理论上确定质量补偿参数最优值，并给出了具体的推导过程。在最优补偿参数基础上，质量提高幅度即质量补偿效果可被定量评估，与其他变量之间的关系也应运而生。本文最后通过实验验证了质量补偿效果及其与其他变量的关系。

2 相关知识

2.1 SVD分解

SVD分解是线性代数中的矩阵分解知识之一，可把任意大小的矩阵分解成奇异向量与奇异值形式。其良好的数值稳健性被广泛应用于图像重建与复原、图像去噪、图像水印等。秩为r(r≤min{M,N})的矩阵A∈RM×N经过SVD分解后得到左奇异矩阵U、奇异值矩阵S与右奇异矩阵V。其中U、V为正交矩阵，S为对角矩阵且对角元素满足s(1)≥s(2)≥…≥s(r)>0。有关SVD的详细知识见文献[18]。用奇异值与奇异向量元素表示的矩阵元素形式为：

(1)

2.2 基于奇异向量鲁棒性的水印算法分析

基于奇异向量鲁棒性的水印算法通过修改某个奇异向量第1列元素的2元素，使2元素绝对值之差落入由嵌入参数决定的不同间隔，以嵌入水印。本文将载体图像标记为A∈RM×N，水印图像为W={wh|1≤h≤L}时，不失一般性，设被修改的2元素为左奇异向量第1列的第2、3个元素，分块大小为4×4，嵌入提取步骤如下所示：

嵌入过程:

步骤2依次对每一分块嵌入1比特水印，具体嵌入步骤如下所示：

(2)

(3)

(4)

步骤3依次为每一分块做反向SVD分解并替代原有图像或变换域子带，直接得到或频域变换后得到水印图像A′。

提取过程:

步骤1与提取过程的步骤1相同，先对原始图像或变换域子带分成4×4块后，依次对选块做SVD分解。

步骤2通过比较每个选块左奇异向量第1列元素中第2、第3个元素之间的关系提取水印比特，具体如下：

(5)

2.3 图像质量补偿

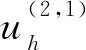
(6)

3 质量补偿分析

3.1 最优补偿参数确定

(7)

不等式(7)的左右两边可分别表示为：

(8)

(9)

(10)

(11)

将式(11)代入式(10)可得：

(12)

(13)

(14)

(15)

3.2 质量补偿与鲁棒性的关系

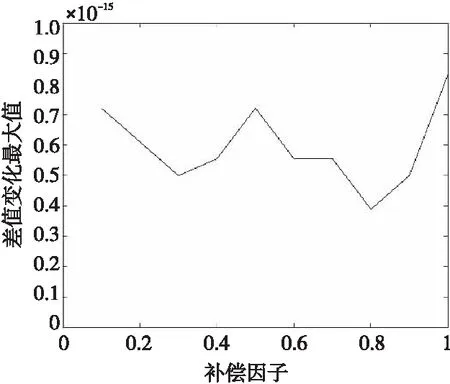
Figure 1 Relationship between the compensation factor and the maximum change value of the difference between the two elements in the left singular vector before and after compensation图1 质量补偿前后的左奇异向量 2元素差值变化最大值与补偿因子之间的关系

3.3 补偿效果分析

确定最优补偿参数后，本文根据式(12)可得:

(16)

4 实验结果

本节将对第3节得出的最优质量补偿参数进行实验验证。本文选取如图2所示的10幅512×512的经典图像做载体，32×32的二进制图像做水印，在DWT低频域通过最大奇异值排序选取32×32个分块，在其左右奇异向量分别嵌入水印与质量补偿。同样基于DWT与奇异向量鲁棒性的水印方法[14]被选做比较方法以验证提出的质量补偿参数的有效性。

Figure 2 Lena， Peppers, Man, Baboon, Couple, Fishingboat, Sailingboot, Barbara, Goldhill, Cameraman and the watermark (32×32)图2 载体图像Lena， Peppers, Man, Baboon, Couple, Fishingboat, Sailingboot, Barbara, Goldhill, Cameraman和32×32水印

定义于式(17)、式(18)的PSNR与定义于式(19)的BER为测试不可见性与鲁棒性的衡量指标。

(17)

(18)

(19)

其中，MSE称作图像的均方误差，MAXA为矩阵A的元素最大值。当设定嵌入参数t为0.55,0.45,0.35,0.25,0.15,0.05时，本文对10幅测试图像做水印嵌入与质量补偿，并记录质量补偿前后的PSNR值。图3显示了PSNR均值与参数t的关系，从中可看出质量补偿对水印图像质量的提升效果。

Figure 3 Effect of quality compensation on PSNR图3 质量补偿对PSNR的影响

本文提出的质量补偿方法的目的是在不损失鲁棒性前提下提升方法的不可见性。因为水印方法的鲁棒性与不可见性为此消彼长的关系，所以质量补偿通过提高水印不可见性，间接提升鲁棒性。考虑到人眼对水印的敏感阈值，本文通过调整量化步长将PSNR设为40左右，并对图2所示的10幅图像做JPEG压缩等处理，再计算提取水印与原水印之间的BER值。表1为与文献[14]方法的鲁棒性比较，从中得知，当图像质量相近时，本文方法面对多数攻击时的鲁棒性优于Makbol等人的方法，这验证了质量补偿对方法性能的提升作用。

Table 1 Performance comparison between the proposed scheme and reference [14]表1 本文方法与文献[14]方法的性能比较

5 结束语

本文针对基于奇异向量鲁棒性水印方法的质量补偿问题展开研究，不仅给出了最优补偿参数的确定方法，并对质量补偿的效果进行了评估。通过理论与实验证明得知，修改奇异向量做质量补偿不仅能提高水印图像质量，且不会对鲁棒性产生影响。但是，修改右奇异向量对图像质量的提高作用有限，如何找到更有效的质量补偿方法是下一步的研究方向。