分时阶梯电价下流水车间节能调度问题研究

闫建涛，肖继明

（西安理工大学 机械与精密仪器工程学院，西安 710048）

0 引言

工业部门消耗的能源占到了全球能源消耗的一半，而工业中90%的电力都是由制造业消耗的。电能作为制造业的主要能源，如何节约电能是制造业不得不考虑的问题。合理的生产调度是可以降低电能消耗、降低生产成本的有效途径之一[1]。为了维护电网稳定，不同的电价政策被实施，引导着电力用户改变其电力消费模式[2]。考虑不同电价政策的生产调度可以在不减少产出的情况下，达到企业降低电力成本的目的。

传统的生产调度侧重于提高生产效率，是以最小化最大完工时间、成本、交货率等为优化目标，近十年来，考虑能耗的生产调度成为了国内外学者研究热点之一。李龙[3]等以车间的生产运作时间，生产成本以及车间能耗为目标，采用遗传算法解决了流水车间绿色生产调度问题，并以流水车间齿轮类零件加工为例，验证了模型的有效性与准确性。孟磊磊[4]等针对不相关并行机调度问题，以能耗最小化为目标，建立5个考虑关机/重启策略的混合整数规划模型，并对比分析了模型的优缺点。Zhang[5]等在考虑机器的加工速度基础上，以加工过程的总加权延迟时间最短和总能耗最小为目标建立模型，并采用多目标遗传算法对其求解。lei[6]等研究了在给定总能耗的情况下，使得完工时间和总延迟时间最小，对柔性作业车间进行建模，并采用帝国竞争算法对问题求解。

分时电价政策是促使电能需求曲线趋于平衡，减少高峰时段用电的一项电力措施[7]。考虑分时电价的生产调度可以改变用电时段，进而有效的减少生产所需的电力成本，达到降低能耗的目的。吴宇娟[8]研究了分时电价下，以最小化总用电成本为目标的相同并行机调度问题，建立了连续时间混合整数线性规划模型，采用禁忌搜索-多级过滤贪婪插入启发式混合算法对问题求解。Moon[9]以最小化完工时间和最小化电力成本为目标，并使用混合遗传算法解决了考虑分时电价的无关并行机调度问题。Zhang[10]研究了分时电价下混合流水车间的调度问题，建立了机床的能耗模型，以最大完工时间和电力成本最小化为目标，采用改进的强度Pareto进化算法进行求解。Wang[11]研究了双机流水车间调度问题，以分时电价下的总电力成本最小化为目标，将问题表示为混合整数线性规划，然后基于Johnson规则和动态规划方法设计两种启发式算法对问题进行求解。Mao[12]在分时电价下针对并行机调度问题，建立了经济批量调整和调度模型，其目标是最小化生产中的电力成本，实现最优的经济调度，最后通过实验结果证明了所提出的模型显著降低了电力成本，并促进了电网的峰值负荷调节。

从已有研究来看，大多数学者都只考虑了分时电价，并对不同的调度车间问题进行了建模求解，有效的降低了能耗。但仅考虑分时电价有其局限性，可能会导致峰谷时段的偏移，分时阶梯电价作为一种新的基于价格的需求侧管理措施被提出[13,14]，是在分时电价的基础上加入了阶梯电价，结合了分时电价的特点（均衡峰谷时段用电量）和阶梯电价的特点（激励用户节能，提高能源利用率），可以更有效地促进用户节能。

流水车间是常见的一种车间生产方式，在复杂度上，2台机器以上的流水车间调度问题被证明是NP-hard问题[15]，因此本文针对流水车间的节能生产调度问题，考虑分时阶梯电价，采用连续时间建模方式，建立生产调度的数学模型，设计算法进行求解，并通过实例验证所建数学模型的正确性以及求解算法的有效性。

1 问题描述

考虑分时阶梯电价的流水车间问题描述如下：有多个多种类的待加工工件，需要依次经过相同的工序进行加工，但不同种类的工件加工时间各不相同，每道工序只有一台机器可以加工。已知工件各道工序在各机器上的加工时间和功率需求，要求在考虑分时阶梯电价的情况下，确定工件的加工顺序及每道工序的开始加工时间，保证在规定的时间内完成加工任务，同时使得加工消耗的电力成本最小。

分时阶梯电价[14]按照电力用户的用电习惯划分时段，将一天时间分为高峰段、平段、低谷段三个时段，并在每个时段设定多级阶梯电价，以两级阶梯电价为例，在低于用电量标准时执行第一阶梯电价，高于用电量标准时，超出部分执行第二阶梯电价，如图1所示。

图1 分时阶梯电价示意图

针对该问题进行如下假设：1）同一时刻，每台机器只能加工一道工序；2）每道工序的加工时间是确定的；3）加工是非抢占式的，每道工序一旦开始加工不能中断；4）夹具装卸等准备时间计入每道工序的加工时间；5）工件的工序固定，每道工序必须在其紧前工序完成之后才能进行后续工序。

2 模型建立

为建立考虑分时电价的流水车间调度模型，引入数学符号定义如下：

n：待加工工件总数；

m：加工设备数，即工件的加工工序数；

s：分时电价划分时段总数；

i：机器编号，i∈[1，m]；

k：工件编号，k∈[1，n] ；

j：加工时段编号，j∈[1，s]；

Ej：加工时段j的耗电量；

Pik：工件k在机器i上的加工时间；

qik：机器i加工工件k时所需功率；

Sik：工件k在机器i的开始加工时间；

Eik：工件k在机器i的加工完成时间；

Emax：最大完工时间；

ST：计划开始时间；

ET：计划结束时间；

PCSjv：j时段第v档阶梯用电量的分界点（单位：千瓦时）；

Pjv：j时段的第v档电价，v∈[1，V]；

如何实现这一突破，实现华裔青少年族群意识的恢复、华族文化的认同、华语能力的掌握及华语水平的提高，数年来一直是老一辈华族、中国政府及华文教育者所思考的问题。中国国务院侨办“寻根之旅”活动的推出，为我们提供了一条解决这一难题的极好途径。俗语说：读万卷书，行万里路，百闻不如一见。“中国寻根之旅”就是培养文化认同最直接、最有效的途径之一。因为，开展此类活动，可以让华裔青少年身临祖籍国，通过耳闻目睹，解决祖籍认同问题，恢复华族自信心，提高民族自豪感，进而自觉地担当起华族优秀文化学习和传承的重任，做一个名副其实的华人。

xjv：j时段用电量是否在第v档范围，若在值为1，否则值为0，v∈[2，V]；

yijk：机器i加工工件k时是否在j时段进行加工，若加工，值为1，否则值为0；

tijk：机器i加工工件k时在j时段加工时长，当=1时，值为pik，否则，说明机器i跨时段加工工件k，需根据工件开始加工时间Sik、所需加工时长Pik和所在时段j的上下限计算该时段内的加工时长。

本文采用连续时间建模，xjv与yijk为布尔变量，是为了便于确定加工时段用电量处于第几档电价和机器i加工工件k时在j时段的加工时间而引入的，因此，不考虑照明等日常用电，只考虑生产机器耗电，建立电力成本最小化的目标函数如下：

考虑约束条件如下：

其中，（1）表示生产过程不被打断，工件k在机器i上的开始时间加上加工时长等于结束时间，保证生产的连续性；（2）表示同一工件同一时刻不能在不同的机床上加工，每件工件k在当前机器i的结束加工时间小于在下一台机器i+1的开始时间，同一工件的前道工序完成加工后才开始后一道工序；（3）表示同一时间一台机器只能加工一个工件，每台机器i加工当前工件k的结束时间小于加工下一件工件k+1的开始时间，同一台机器加工完上一件工件后才能加工下一件工件；（4）、（5）、（6）、（7）表示要在规定时间内完成加工任务，开始加工时间和结束加工时间都必须在规划时间内。

3 算法设计

考虑分时阶梯电价的流水作业车间调度问题具有较高的复杂性，从流水作业车间生产调度的角度分析，需要考虑多个工件的加工顺序，并计算各工件每道工序的开始加工时间和完工时间；考虑分时阶梯电价后，不仅需要考虑加工顺序，更需要在规定的时间范围内针对各工件的开工时间进行合理的错峰安排，才能最终确定各工件的开始加工时间，使得问题更加复杂。因此，针对该问题，本文采用具有强大全局寻优能力的遗传算法进行求解。

3.1 编码

考虑分时阶梯电价的流水作业车间问题需要考虑工件的加工顺序和作业开始时间，因此采用实数编码，将整条染色体分为两部分：工序码+时间码，第一部分是工序码，基于工件的加工顺序进行编码，第二部分是时间码，表示工件在每台机器上的开始加工时间。

假设有4个代加工工件，每种工件有3道工序，对应的有3台机器可以进行加工，设计一个可行解[3 3 3 2 2 2 1 1 1 4 4 4 | 0 5 11 5 11 18 6 13 21 7 15 24]，可行解分为两部分，竖线前面的为工序码，采取基于工序的编码方式；竖线后面的为时间码，表示与工序码相对应的开始加工时间。本文编码设计将工序码和时间码结合起来，工序码确定工件的加工顺序，时间码确定机器开始加工时间，方便统计机器在某个时段内的加工时间和电力需求。

3.2 初始种群产生

图2 染色体工序码交叉操作

初始种群产生，在产生能在规定时间内的工序码后，时间码有两种产生方式，前50%的种群采取完工时间尽可能短的方案，首件工件的首道工序从计划开始时间加工；后50%的种群采取完工时间尽可能长的方案，末件工件的末道工序在计划结束时间完工。两种不同的时间码产生方式，保证种群时间码的多样性。

3.3 交叉算子

交叉算子分为两种，针对工序码的交叉采用POX（precedence operation crossover）交叉算子，POX交叉算子可以很好的保留父代优良特征，继承父代的加工顺序，并且保证子代的可行性，如图2所示；针对时间码的交叉采用两点交叉，随机选中两点，互换两点之间的部分，时间码交叉后可行性不易保证，因此采用后期修复的方法，保证子代的可行性。

3.4 变异算子

变异算子分为两部分，第一部分对基于工序的工序码变异，第二部分是针对时间码变异，本文采用两点互换操作，在相应部分任意选择两个互换点，然后互换对应位置的编码，并对时间码进行修复，此变异操作方法可以保证编码的合法性。

3.5 选择算子

选择算子需要将本代种群中适应值较高的染色体保留到下一代以保证种群朝着更优的方向进化，本文编码包含工序码和时间码，因此以目标函数电力成本的倒数作为适应度函数，采用轮盘赌法进行选择，保证符合要求的染色体可以保留到下一代。

3.6 算法流程

因为编码包含了基于工序的工序码和工序开始加工时间的时间码，因此算法分为两部分，首先是工序码的迭代，在工序码能保证在规定时间内完成任务后，再对时间码进行迭代，促使电力成本最低。因此，设计算法流程图如图3所示。

4 实例分析

图3 算法流程图

针对某考虑分时阶梯电价的流水车间调度问题：某车桥加工车间共有6台机器，现有4种工件，每种各5件，共20件工件需要加工，计划从早上7点开始加工，要求40个小时内完成加工任务（包括一个低谷时段，四个平峰时段，四个高峰时段）。每种类型工件的加工时间和功率需求如表1所示。

表1 各机器加工时间及功率

参考现行的陕西省分时电价和居民阶梯电价，假设每个时段有两档电价，构建本文的分时阶梯电价模型。第一档为正常用电，第二档为高标准用电，假设每时段电力价格如表2所示。

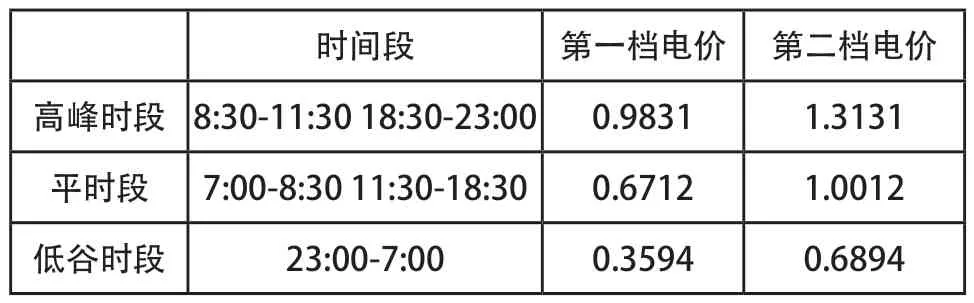
表2 分时阶梯电价时段及价格表

分时阶梯电价的分界点根据每天峰平谷三个时段的长度确定，取高峰段，平段，低谷时段用电量第二档电价分界点分别为750千瓦时/天、850千瓦时/天、800千瓦时/天。

在考虑分时阶梯电价下，本文以电力成本最小化为目标，设置种群规模为50，种群迭代次数为600，时间码迭代次数为300。迭代10次得到最优调度方案甘特图如图4所示，同时以最小最大完工时间为目标作为对照组，得到最优调度方案甘特图如图5所示。对比两组的电力成本如表3所示。

图4 以电力成本最小化为目标的最优调度方案甘特图

图5 以最小最大完工时间为目标的最优调度方案甘特图

表3 考虑不同目标的调度结果对比

从图4中可以看出，考虑分时阶梯电价的生产调度可以在规定的时间内完成加工任务并有效的进行错峰生产，从表3的对比数据中可以看出，考虑分时阶梯电价的情况下，以本文所建立出的模型，求解出的调度方案使得电力成本降低了34%，有效的降低生产所需的能耗。

5 结语

本文综合考虑了分时电价和阶梯电价，针对流水车间调度问题建立了数学模型，并针对建立的数学模型设计了基于工序编码和时间编码的遗传算法，最后以实例验证了该问题数学模型的正确性和求解算法的有效性。结果表明，在分时阶梯电价下，以最小化电力成本为目标，进行生产调度决策，可以有效的进行错峰生产，显著的降低电力成本。本文只考虑了工件加工过程中的能耗，在未来的研究中，将考虑加入非加工过程产生的能耗，如等待能耗，开关机能耗等，进一步提高问题的实际意义。