静电除尘器极板配置形式与场内颗粒迁移规律数值模拟研究
2020-10-10陈兵郭永恒李宏姣刘柏谦章干养赵海宝
陈兵,郭永恒,李宏姣,刘柏谦,章干养,赵海宝
CHEN Bing1,GUO Yongheng1,LI Hongjiao1,LIU Baiqian1,ZHANG Ganyang2,ZHAO Haibao2
(1.北京科技大学机械工程学院,北京100083;2.浙江菲达环保科技股份有限公司,浙江诸暨311800)
(1.School of Mechanical Engineering,University of Science and Technology Beijing,Beijing 100083,China;2.Zhejiang Feida Environmental Science and Technology Company Limited,Zhuji 311800,China)
0 引言
在过去的几十年中,随着城市化和工业化的快速发展,空气污染已成为当今人类面临的最严峻的全球挑战之一。联合国在最新的《全球环境展望》报告中称,恶劣的环境条件造成全球约25%的人口罹患疾病或死亡[1]。空气污染导致肺癌等疾病频发,每年造成600万~700万人早逝,而这一污染的主要源头为化石燃料燃烧释放的烟气。目前火力发电在世界上占有很大的市场份额,而火电厂排放的大量烟气已成为造成我国雾霾天气的一个不容忽视的原因[2-3]。作为火电厂的污染物排放控制装置,静电除尘器(ESP)在环境保护中起着重要作用[4]。但是,由于污染物排放标准的逐步严格,对静电除尘器的性能提出了更高的要求。建立清洁、低碳、安全和高效的ESP 系统迫在眉睫,研究各种极板配置下的电晕放电和颗粒迁移仍然是非常有意义和挑战性的。
为了全面了解ESP 中的电场和颗粒行为,近年来学术界及工业界已展开了大量的试验和数值研究,以便更好地了解ESP的结构。文献[5]研究了在2 个带有波纹板和平行板的静电除尘器中,在不同气体速度下具有不同施加电压的电流体力学(EHD)。在不同极板配置下,线板静电除尘器的许多放电特性已通过试验研究,包括放电极的电晕放电的几何研究[6]。目前已经进行了许多试验来研究具有不同形状、直径和间隔的放电极的放电特性[7]。与试验方法相比,数值模拟是优选的,因为它灵活性高、成本低、精度相对较高[8]。研究在ESP 中电晕放电和颗粒去除过程已有若干成熟的数值模型[9]。例如,文献[10]提出了一种改进的数值模型,用于计算线-板静电除尘器中电晕放电感应的电场,使用有限差分法(FDM)在正交曲线坐标系中求解电势方程。文献[11]提出了一种简化的物理模型,以提高计算效率并克服先前模型在电极线表面电场方面的局限性,但是仍存在一些不可避免的缺陷。例如,无法处理特殊的放电极几何结构以及计算成本较高的问题[12]。此外,有关所述颗粒的空间电荷效应及反电晕放电的一些异常情况仍需进行更多研究,因为它们可能会削弱电场并影响颗粒收集[13-15]。
目前,大多数研究仅集中于收尘板的类型或放电极的结构,很少有考虑到不同形状的放电极和收尘板的配置所产生的影响。随着新型ESP类型和极板配置的不断发展,为提高超细颗粒(如PM2.5)的去除效果,放电极构造变得越来越复杂。因此,系统地研究复杂的极板配置对电晕放电、颗粒带电,以及颗粒迁移都是非常有意义的。
本文基于COMSOL Multiphysics 仿真平台,对6种不同极板配置下的静电除尘器特性展开仿真研究。COMSOL Multiphysics 是一个基于高级数值方法,用于模拟仿真物理场问题的通用软件平台。借助COMSOL Multiphysics 可将传统的单场模型轻松扩展为同时求解耦合物理现象的多物理场模型。本文根据不同极板配置对电除尘器的电场特性、气流分布特性和收尘效率的影响规律进行了研究。首先,采用有限元法求解不同收尘板下的空间电荷密度分布和电流密度分布;其次,采用k-ω湍流模型描述气流的分布特征,发现不同极板配置对离子风的影响规律;最后,用拉格朗日方法描述颗粒运动,计算极板配置形式对收尘效率的影响规律。文中所开展的各项工作,为电除尘器的放电极结构选择与优化提供了数值分析依据。
1 控制方程和数值解析方法
1.1 电晕放电
当放电极连接到一定的高压时,由于电晕放电,在导线附近形成电离区,空气电离成正离子和负离子。正离子向导线移动,负离子向收尘板移动。此时,ESP 中的剩余区域称为漂移区。负离子与穿过该区域的尘埃颗粒碰撞,使之荷电。
静电除尘器内电晕放电由以下控制方程耦合作用,满足泊松方程:

且服从电流连续性方程:

电势与电场之间的关系由下式定义:

式中:φ 为电势,V;E 为电场强度,V∕m;J 为电流密度,A∕m2;ρ 为空间电荷密度,C∕m3;ε0为真空介电常数,F∕m;Zion为离子迁移率,m2∕(V·s);D 为扩散系数,m2∕s。
正常情况下,在电流连续方程中扩散项远远小于导电项,故忽略扩散电流。Kaptzov 假设用于设置放电极上的电场强度,认为在电晕放电后阴极表面上的场强保持恒定,并且其值为起晕阈值的场强,由Peek经验公式计算[14]:

式中:E0为起晕电场强度,V∕m;rc为放电极半径,cm。本文利用COMSOL 5.2帮助手册求解电场的边界条件。
1.2 湍流运动
电除尘器工作时,含有大量粉尘颗粒的气流进入电除尘器。由于气体离子受电场力的影响,气流的流型也受到通过离子风方式的电场干扰。为了研究气流流型,采用稳态雷诺平均质量连续性和动量守恒方程来求解气流流速uf和压力p。
动量守恒方程:

式中:I 为单位矩阵;uf为气流流速,m∕s;p 为压力,Pa;ρf为 气 流 密 度,kg∕m3;k 为 湍 流 动 能,m2∕s2;ρ(-∇φ)称之为体积力,它是电场作用在气流上的直接体现。本节通过湍流模型模拟电除尘器内的气流流动,并采用k-ω 方程求解湍流动能k 和比耗散率ω,其一般方程如下。
湍流动能控制方程:
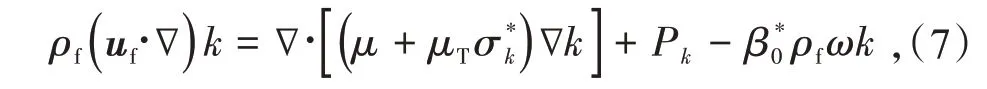
比耗散率方程:
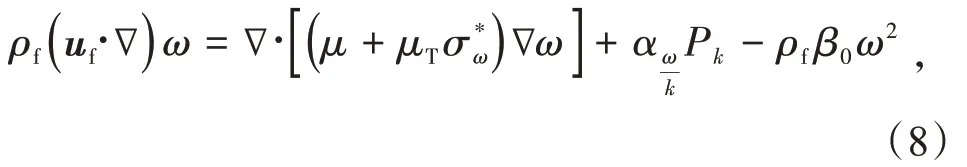
其中:

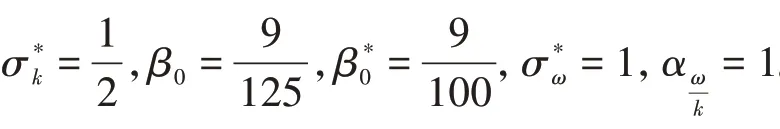
1.3 颗粒荷电及运动机理
颗粒荷电是决定颗粒行为的一个完整过程。目前荷电机理主要包括场致荷电和扩散荷电。文献[16]提出的配置充电模型被证明能够处理微米级颗粒并达到令人满意的精度,其计算公式如下:
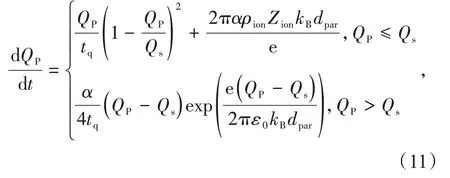
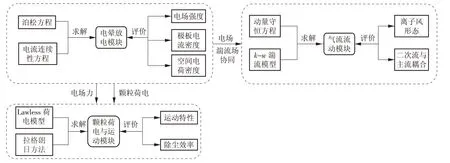
图1 颗粒荷电及运动的研究流程Fig.1 Research on the charging and movement of particulars
其中

式中:Qs为颗粒的饱和电荷量,C;QP为颗粒到达某一处的电荷量,C;α 和v 为模型常数;εr为粉尘颗粒的相对介电常数,F∕m;kB是玻尔兹曼常数,J∕K;dpar为颗粒直径,μm;tq是颗粒充电的时间常数,s;T 为温度,K;ρion为空间电荷密度,C∕m3。
在对颗粒运动特性进行分析时,更关注单颗粒的特征,故将颗粒运动特性认为是离散相,且使用拉格朗日运动模型来描述。ESP内的颗粒在电场荷电及扩散荷电的作用下荷电,荷电后的颗粒除了受电场力的作用外还受到空气流场产生的曳力及重力作用,在合力作用下实现向收尘板的运动。
根据牛顿第二定律,其运动方程可以写成
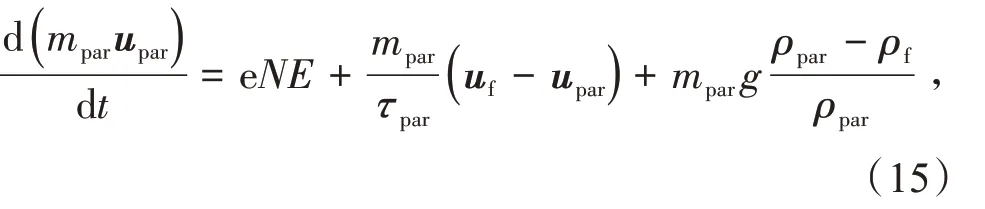
其中

式中:mpar为颗粒质量,kg;ρpar为颗粒密度,kg∕m3;N为电荷数;upar为颗粒运动速度,m∕s;g 为重力加速度,m∕s2。图1为颗粒荷电及运动的研究流程。
2 模型条件及验证
ESP 模型由2 个接地的收尘板和位于2 个板之间并施加高负电压的3个圆形放电极组成。收尘板间距为180 mm,长度为480 mm,放电极间距为100 mm,第1 个放电极与通道入口之间的距离为140 mm。3 种收尘板和2 种放电极的ESP 示意图如图2所示。

图2 3种收尘板和2种放电极的ESP示意Fig.2 ESPs with three different dust collecting plates and two different electrodes
为了验证本方法的准确性,将数值模拟结果与其他试验的数值模拟结果进行比较。图3为43.5 kV和25.5 kV 时从放电极到收尘板的电位变化。虚线为本试验的数值模拟结果,离散点是文献[17]的数值模拟结果。

图3 数值仿真模型验证Fig.3 Verification for numerical simulation models
3 数值模拟分析与讨论
本节从电场特性、气流和收尘效率等方面对6种极板配置下的静电除尘器性能进行了比较。释放颗粒100个,直径为5×10-7m,颗粒密度为900 kg∕m3。在入口流速为1 m∕s,供电电压为36 kV的情况下,分析不同极板配置下静电除尘器内部电晕的放电特性;在供电电压为36 kV 和入口流速分别为0,1,2 m∕s 时讨论不同极板配置下静电除尘器内的气流分布;在供电电压为36 kV,入口流速为1 m∕s 时,研究不同极板配置下的静电除尘器对收尘效率的影响。模型的网格划分采用COMSOL Multiphysics 仿真平台中的自由三角形网格,完整的网格包含7 132 个域单元和392 个边界元。本研究分为3 个研究模块,如图1 所示,电晕放电模块使用COMSOL Multiphysics 仿真平台中的一般形式偏微分方程、点常微分方程、微分代数方程、弱形式偏微分方程,求解器选择COMSOL Multiphysics 仿真平台中的默认稳态求解器;气流流动模块使用k-ω湍流方程,求解器选择默认稳态求解器;颗粒荷电与运动模块使用流体流动颗粒追踪方程,求解器选择默认瞬态求解器。
3.1 电晕放电特性
在入口流速为1 m∕s,供电电压为36 kV 的情况下,图4展示了不同电晕放电极下的电场强度分布,2 种不同的线型代表2 种放电极的2D 形状,放电极的不同形状会影响放电极附近的电场强度。当放电极形状从针刺形变为圆形时,放电极表面的电场强度从1.3×107V∕m 下降到5.2×106V∕m,电场强度达到预期值,由于放电极表面平坦,在圆形放电极下,电场强度较低。相反,由于针刺形放电极放电表面最尖锐,因此会产生最高的电场强度,导致起始电压最低。当ESP通道内烟气被确定的电场电离时,此起始点是临界边界,此时的电压称为起晕电压。

图4 不同电晕放电极下的电场强度分布Fig.4 Electric field intensity distribution with different corona discharge electrodes
在入口流速为1 m∕s,供电电压为36 kV 的情况下,480C 型板各放电极电场强度分布如图5 所示。由图5 可知,在2 种放电极下,电场分布相似,因此可见不同的放电极对电场分布的影响较弱。然而,由于每个放电极的极性均匀一致,在放电极附近形成了较高的电场强度,在2 个放电极之间形成了较低的电场强度。此外,对于480C 型板,电场强度从放电极到收尘板急剧下降。
480C 型板空间电荷密度分布及电流密度分布如图6,7 所示。由图6,7 可知,在2 种放电极下,空间电荷密度和电流密度分布极为相似。在放电极处出现电荷密度极大值,且以此为圆心,呈椭圆状向外扩散并衰减。随着放电极形状的不同,电荷密度的分布也随之改变。针刺形放电极空间电荷密度峰值为12×10-4C∕m3,圆形放电极空间电荷密度峰值为7×10-4C∕m3。

图6 480C型板空间电荷密度分布Fig.6 Space charge density distribution of a 480C pressed plate
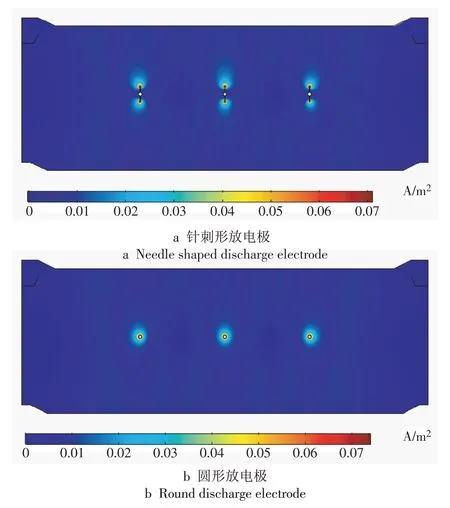
图7 480C型板电流密度分布Fig.7 Current density distribution of a 480C pressed plate
收尘板之间放置3 根放电极,形成放电极和收尘板的6 种配置。图8 为沿收尘板方向的6 组极板配置下的电流密度分布。尽管电流密度总体分布趋势相似,但不同形状的放电极对收尘板表面附近的电流密度影响显著。电流密度为周期性变化,针刺形放电极-波纹板在6 种配置中具有最高的电流密度,其次是针刺形放电极-480C 型板和针刺形放电极-平板,这归因于不同类型的放电极具有不同的电势分布。此外,观察到放电极的复杂结构对波形板侧面附近的电流密度分布有很大影响,由于波形板具有凹凸结构,其最尖锐的放电表面可以产生电流密度峰值。
3.2 静电除尘器内流场分布特性
放电极形状的差异导致空间中不同的电场特性,这直接影响离子风的强度,进而影响离子风对主气流的干扰程度。本节集中比较了针刺形和圆形放电极对气流分布的影响。
当主气流流速为0 m∕s 时,针刺形放电极-平板配置在每个放电极周围产生4 个漩涡结构,且上游和下游处的漩涡较大。此外,漩涡的形状和大小明显受放电极结构的影响,如图9所示。
当主气流流速为1 m∕s时,气流的分布是主气流和二次气流耦合的结果,从气流分布特性可以看出,此时二次气流占主导地位,如图10 所示。在2种放电极下,气流流速分布有极大的相似性,即在水平经过第1,2根放电极后,气流流速明显减小,甚至形成漩涡结构,在水平接近第2,3根放电极时,气流流速急剧增大。此外,当使用针刺形放电极时,收尘板附近区域存在小漩涡结构。

图8 6种极板配置下的电流密度分布Fig.8 Current density distribution with six electrode⁃plate configurations
当主气流流速度达到2 m∕s时,主气流占据主导地位,通道内漩涡结构几乎消失,气流分布相对均匀,如图11 所示。当使用圆形放电极时,气流分布呈波浪状,空间内几乎没有漩涡。但当使用针刺形放电极时,收尘板附近仍存在小漩涡,其很可能带走已经沉淀在收尘板上的粉尘,导致二次扬尘的发生。工业上,应尽可能避免这种现象的发生。
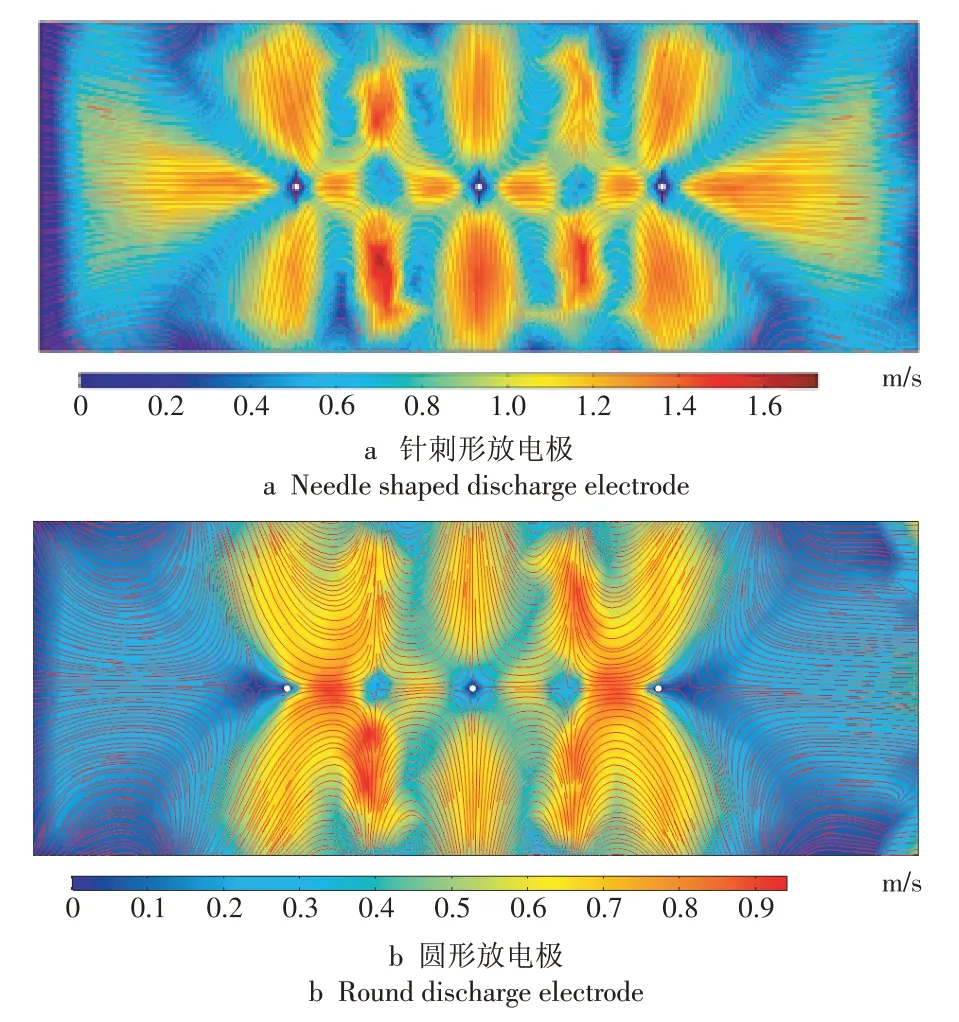
图9 主气流流速为0 m/s时2种放电极的气流分布特性Fig.9 Air flow distribution with two electrodes when the main air flow velocity is 0 m/s
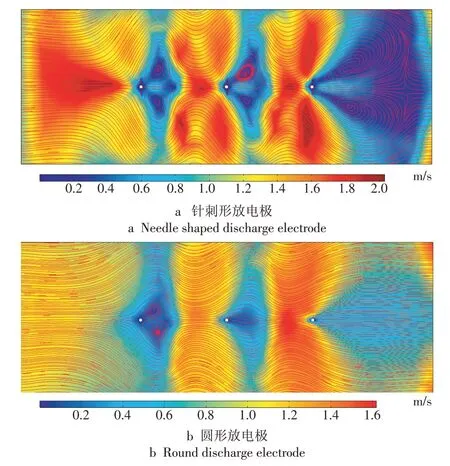
图10 主气流流速为1 m/s时2种放电极的气流分布特性Fig.10 Air flow distribution with two electrodes when the main air flow velocity is 1 m/s
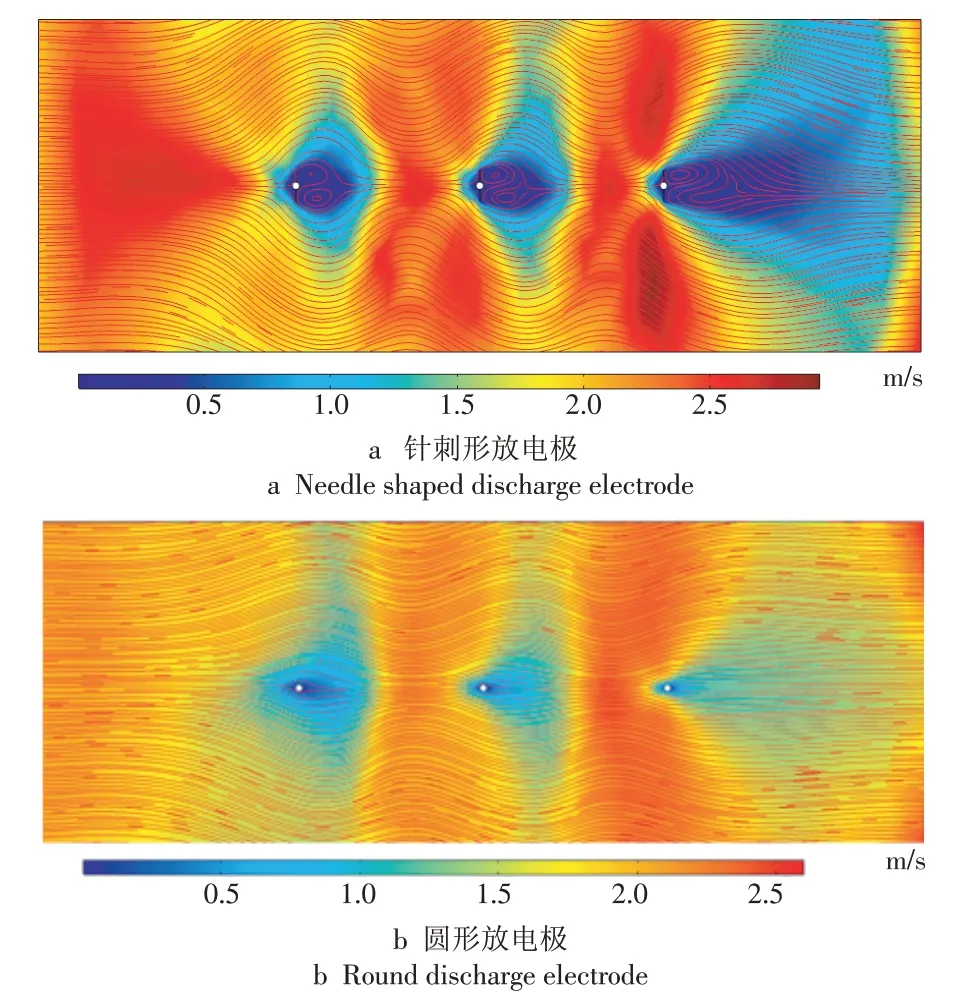
图11 主气流流速为2 m/s时2种放电极的气流分布特性Fig.11 Air flow distribution with two electrodes when the main air flow velocity is 2 m/s
综上所述,放电极的形状对气流分布特征有非常显著的影响,主要表现在:(1)2 种放电极下的离子风形态大体一致,但漩涡结构的大小和形状受到收尘板的限制;(2)离子风的影响不容忽视,当主气流流速为1 m∕s时,通道内气流流速明显大于主气流流速;(3)使用针刺形放电极时,收尘板附近仍存在小漩涡,易造成二次扬尘现象。
为了进一步量化不同放电极的气流分布特性,提取了第2根放电极至收尘板竖直方向上的气流流速,对针刺形放电极-平板和圆形放电极-平板2 种配置下的气流分布进行了深入分析。
图12为入口流速为0 m∕s时,第2根放电极至收尘板竖直方向的气流流速。由图12可见,气流流速先增大后减小,在放电极处达到最低值。在圆形放电极-平板配置下,离子风最大速度从0.48 m∕s增大到0.65 m∕s,在放电极附近为离子风速度的极小值。在针刺形放电极-平板配置下,离子风最大速度从0.87 m∕s 增大到1.27 m∕s。当使用针刺形放电极时,离子风最大速度增加明显。由此可见,放电极形状对气流流速的影响较为显著。

图12 不同放电极下的气流流速Fig.12 Air flow velocity under different discharge electrodes
3.3 颗粒迁移和收尘特性
通常含尘烟气中颗粒粒径分布差异较大,不同极板配置下的颗粒运动轨迹有很大不同。为进一步探究这一现象,本节针对3 种收尘板和2 种放电极的6 种配置下颗粒轨迹和收尘效率进行分析,提取了在40 kV 电压下,气流流速为1.2 m∕s 时,1 000个颗粒在xy平面内的运动轨迹。
图13 比较了6 种极板配置下的颗粒轨迹。沿着收尘板的中心位置释放颗粒,针刺形放电极-平板、针刺形放电极-480C型板和针刺形放电极-波纹板配置下的颗粒能够沉淀至收尘板,而圆形放电极-平板、圆形放电极-480C 型板和圆形放电极-波纹板配置下的颗粒在达到收尘板前就已从出口逃出,且出口高度最高的是圆形放电极-480C 型板配置。在x=0.14,0.24,0.34 m 处分别有2 根放电极,故在该位置处,颗粒在竖直方向上有较大的位移。在2个放电极之间,由于场强较低,颗粒速度减慢。
在供电电压为36 kV,气流流速为1 m∕s时,仿真计算得到不同极板配置对收尘效率的影响,结果如图14所示。
从图14 中可以看出,和圆形放电极相比,针刺形放电极收尘效率更高。在6 种极板配置下,针刺形放电极-480C 型板可获得最高的收尘效率,约85%;圆形放电极-波纹板收尘效率最低,约50%。当放电极形状从针刺形变为圆形时,收尘效率降低。不同的收尘板类型,下降幅度不同,在圆形放电极-480C型板下可获得最高的收尘效率。由此可以得出结论,ESP的收尘板优选480C型板。
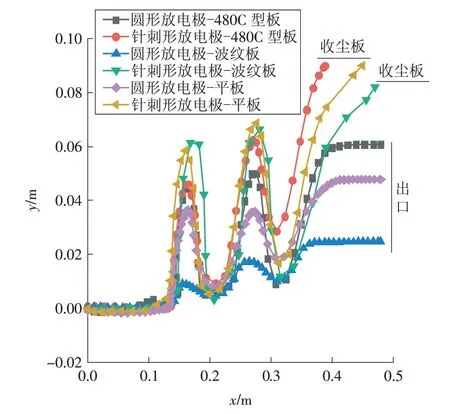
图13 6种极板配置下的颗粒轨迹Fig.13 Particle trajectories with six electrode⁃plate configurations

图14 不同极板配置下的收尘效率Fig.14 Dust removal efficiency with different electrode⁃plate configurations
4 结束语
为探究静电除尘器极板配置形式与场内颗粒迁移间的规律,本文通过数值解析的方法建立了静电除尘系统数学模型,研究了6 种极板配置下静电除尘器的收尘性能,如电场强度、电流密度分布、颗粒轨迹和收尘效率,结论如下。
(1)放电极和收尘板的形状会显著影响静电除尘器的放电特性。针刺形放电极表面附近呈现出电场强度和电流密度的峰值比圆形放电极高,且电流密度分布受收尘板凹凸结构的影响,在收尘板最尖锐的放电表面可以产生电流密度峰值。
(2)放电极的形状对气流分布特征有非常显著的影响。当使用针刺形放电极时,离子风最大速度明显增加。此外,在气流流速达到2 m∕s 时,使用针刺形放电极,收尘板附近仍存在小漩涡,易造成二次扬尘。
(3)不同极板配置将影响颗粒的轨迹和收尘效率。针刺形放电极具有很高的荷电性能,480C 型板具有良好的颗粒收集性能。6 种极板配置下,针刺形放电极-480C型板配置具有最高的收尘效率。
(4)不同条件下,优化放电极和收尘板结构对提高电除尘器的性能具有重要意义。
