基于反向学习的微种群教与学优化算法及其应用

范勤勤，柳缔西子，王筱薇，韩 新，王维莉

(1.上海海事大学 物流研究中心，上海 201306；2.上海交通大学 电子信息与电气工程学院，上海 200237；3.同济大学 上海防灾救灾研究所，上海 200092)

0 引言

教与学优化算法(teaching-learning-based optimization，TLBO)是Rao等[1-2]于2011年提出的一种新的智能优化算法，它主要模拟老师的“教”过程和学生的“学”过程。由于教与学算法具有参数少、算法易于实现、寻优性能好等优点，受到学者的关注和研究[3]。目前，教与学优化算法已被成功地应用于多个领域。

一般来说，小的种群规模(微种群)会加速优化算法收敛，但会使其全局探索能力下降[4]，即易陷入局部最优。因此，为提高微种群优化算法的全局探索能力，众多学者对其进行研究。例如，Ren等[5]提出一种小种群的差分进化算法(differential evolution using smaller population,DESP)。在该算法中，变异策略使用额外的扰动来提高其全局搜索能力，并使用一种自适应调整策略来控制扰动的强度。Brown等[6]提出一种微种群的JADE(adaptive differential evolution with optional external archive)算法。该算法在Rcr-JADE算法[7]的基础上进行改进，并加入了新的差分变异策略来提高算法的全局搜索能力。Marquez-Grajales等[8]提出了μJADEε算法。该算法将ε约束方法用于μJADE算法，以此来提高μJADE算法求解约束优化问题的能力。Salehinejad等[9]提出一种向量化随机变异因子的微种群差分进化算法(micro-differential evolution with vectorized random mutation factor，MDEVM)。在该算法中，每个个体均有各自的差分变异因子F，以此来提高种群多样性。上述研究表明，提高微种群启发式算法的全局搜索能力是避免算法“早熟收敛”的有效方式之一。

博弈论又称对策论，是研究具有冲突和对抗性质现象的数学理论和方法，在很多科学领域中得到了广泛的应用。在博弈问题中，非合作博弈纳什均衡是其最核心的研究内容。1951年，Nash[10]在提出的“纳什定理”中揭示并证明了博弈纳什均衡解的存在，但是Nash并没有给出求解纳什均衡的一般性方法。传统方法在求解纳什均衡问题时均存在一定的局限性，特别是对于高维的博弈模型(如3维及以上的矩阵策略)，传统算法计算复杂且求解成本较高。最近几十年来，随着元启发式算法的迅速发展，诸多学者开始使用遗传算法[11]、免疫算法[12]、粒子群算法[13]、蚁群算法[14]等来求解博弈纳什均衡问题，并取得较好结果，这为求解非合作博弈问题提供了一种新的有效途径和方法。

为进一步提高微种群TLBO算法的全局搜索能力并有效地求解非合作博弈问题，笔者提出一种OBL-μTLBO算法。在该算法中，微种群有利于加快TLBO算法的收敛速度，而反向学习有助于提高TLBO算法的全局探索能力。实验结果表明，OBL-μTLBO 算法的整体性能明显优于其他所比较微种群和非微种群算法。最后，将改进的算法应用于非合作博弈问题的求解，所得结果明显好于其他比较算法。

1 反向学习

反向学习(opposition-based learning,OBL)是Tizhoosh[15]于2005年提出的一种应用于计算智能领域的机器学习方法。因为反向学习策略具有较强的探索能力[16]，所以被广泛地用于提高元启发式算法的搜索性能。一些术语介绍如下。

反向数(opposite number)：设存在实数x∈[a，b]，则与其对应的反向数xo被定义为：

xo=a+b-x,x∈[a,b]。

(1)

反向点(opposite point)：对于D维的搜索空间，设Xi=(xi,1,xi,2,…,xi,D)为其解向量空间内的一个点，且xij∈ [aj，bj](j=1,2,…,D)，则与其对应的反向点表示为：

(2)

另外，Wang等[17]于2011年提出一种广义的反向学习策略(generalized opposition-based learning,GOBL)，其反向个体生成如下：

(3)

式中：r是被用来控制反向解的搜索范围。研究表明，GOBL策略可以有效地使算法跳出局部最优[18]。

2 基于反向学习的微种群教与学优化算法

2.1 基于反向学习的“教”阶段

对于微种群而言，由于种群规模较小，因此种群多样性更容易迅速丢失。故笔者将结合GOBL策略，在教学阶段使用反向学习个体XGO来指导种群进化，从而提高微种群教与学优化算法的探索能力。其反向个体更新方式如下：

(4)

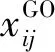
Xi,new=Xi,old+N(0.5,0.2)·(XT-TF·XM)+

N(0.5,0.2)·(XGO-Xi,old)，

(5)

式中：N表示正态分布函数。若Xi,new的适应度值优于Xi,old，则更新个体；否则，不更新。

2.2 OBL-μTLBO算法的实现步骤

Step1初始化。设定微种群规模NP，最大评价次数FES；初始化种群。

Step2教学阶段。根据式(5)对个体进行更新，并对个体进行选择。

Step3学习阶段。根据文献[19]利用正态分布随机数代替式(2)的均匀随机数，其更新公式如下：

(6)

Step4判定算法是否达到最大适应度评价次数，若没有达到，则跳转至Step 2继续执行；如达到，则执行Step 5。

Step5输出结果。

3 仿真测试

为验证OBL-μTLBO算法的有效性，笔者选取文献[6]中13个30维的测试函数。其中f1～f7为单峰函数，f8～f13为多峰函数。OBL-μTLBO算法性能分别与TLBO[1-2]、DESP[5]、μJADE[6]、Rcr-JADE-s4[7]、MDEVM[9]、TLBO-CSWL[19]、FSADE[20]、ODE[21]以及MDEVM-Fajfar[22]等微种群或非微种群算法进行对比。对于每个测试函数，所有比较算法均独立运行50次。同时，为保证所得结论的可靠性，仿真结果采用Friedman[23]、Bonferroni-Dunn[24]、Iman-Davenport[25]、Holm和 Hochberg[25]检验进行统计分析。显著性水平设定为5%。此外，所得最好结果在表中用黑体表示。

3.1 与微种群算法的比较

在该实验中，本文算法OBL-μTLBO与其他5种微种群算法进行比较，并通过设定的求解精度来比较哪种算法所使用的适应度函数评价次数最小。对于所有比较算法，实验参数设置均与文献[19]一致。即种群规模设定为8，对于f7，函数的结果精度设定为1.0E-02，其余测试函数的寻优精度设定为1.0E-08,最大适应度函数评价次数为3 000 000。若算法在达到终止条件时仍然没有求解到设定的求解精度，则认为算法在该函数上寻优失败，用“—”表示。仿真结果如表1所示。由表1可知,OBL-μTLBO算法在计算f1、f2、f3、f4、f5、f6、f7、f8、f9、f10、f11、f12上使用的函数评价次数最少，寻优效率明显优于其他所比较算法。这说明OBL-μTLBO算法不仅可以加速收敛，还可以提高寻优性能。对于函数f8和f13，μJADE算法的仿真结果略优于OBL-μTLBO算法。其主要原因可能是：虽然反向学习能够有效地帮助TLBO提高全局搜索能力，但是差分进化算法的全局搜索能力要好于TLBO算法。除以上比较外，还使用非参数的统计分析方法来对实验结果进行进一步分析，所得统计分析结果见表2和表3。从表2中可知，OBL-μTLBO算法在所有算法中的寻优效率是最高的。从表3可以看出，OBL-μTLBO算法的寻优效率要显著优于DESP、MDEVM、MDEVM-Fajfar算法，OBL-μTLBO算法的整体性能要比μJADE好。综上所得，OBL-μTLBO算法的收敛速度在所有比较算法中是最快的，且可得到高质量的解。

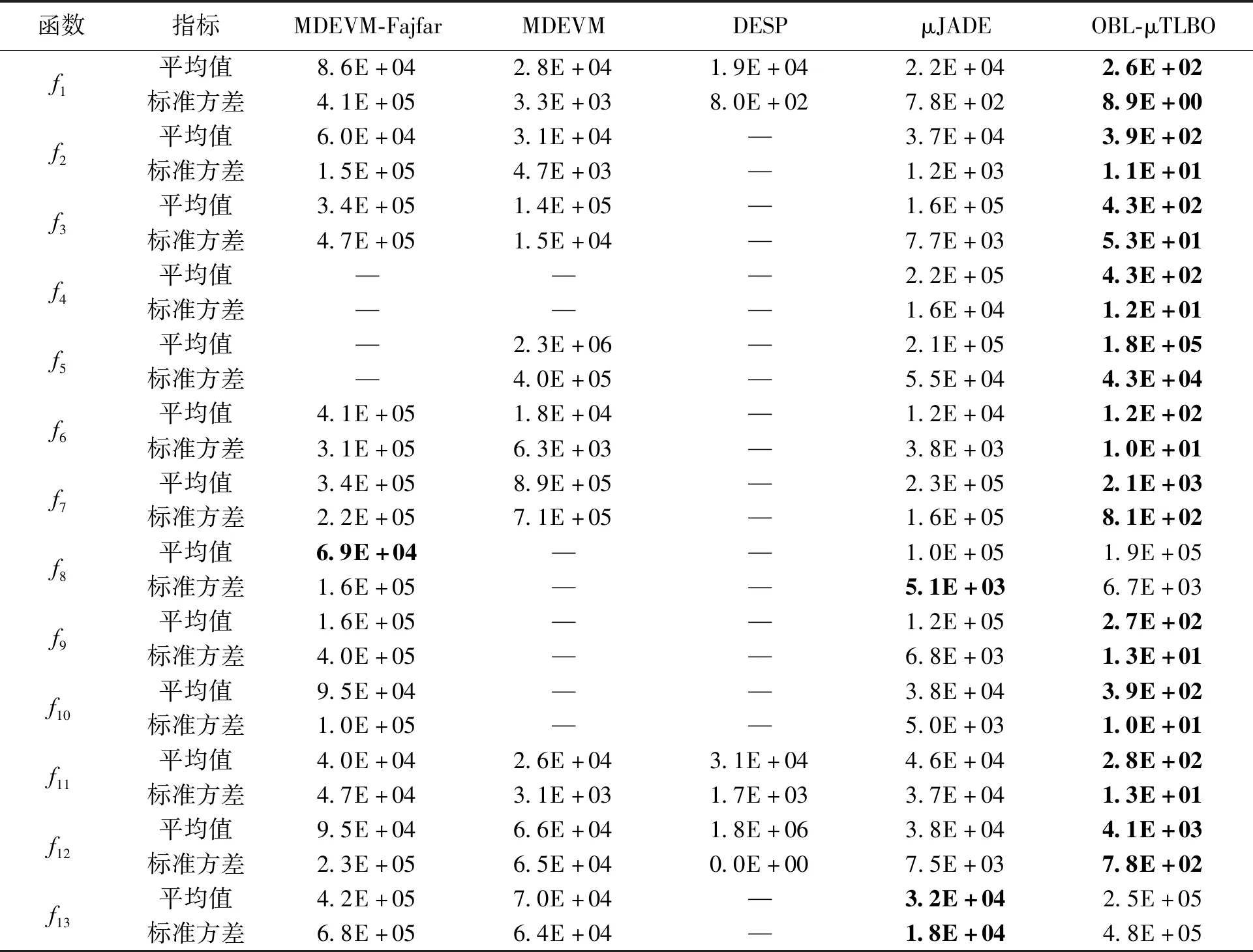
表1 微种群算法的实验结果Table 1 Experimental results of micro-population algorithms

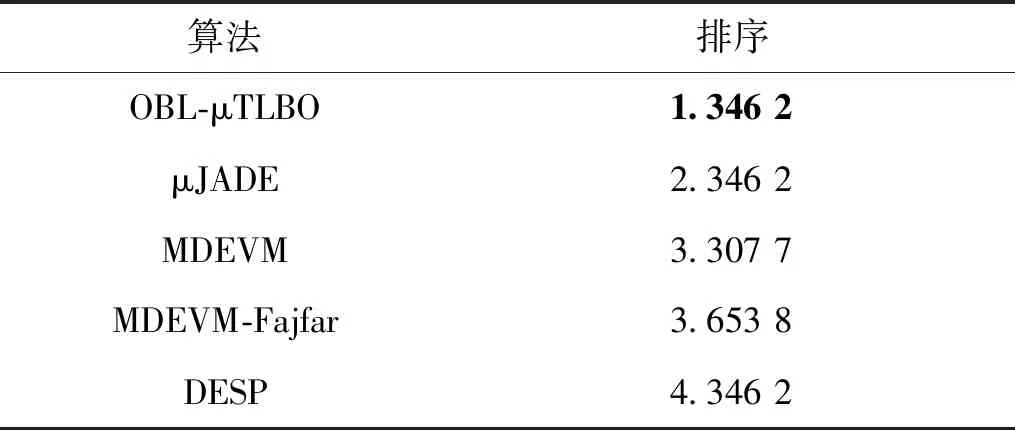
表2 Friedman测试在微种群算法上所得排序结果Table 2 Ranking obtained by Friedman′s test for micro-population algorithms

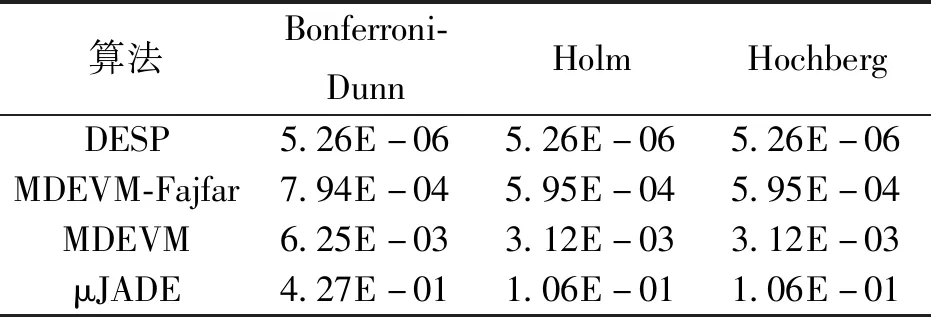
表3 Bonferroni-Dunn、Holm和Hochberg在OBL-μTLBO和微种群算法上所得p值Table 3 p-values obtained by Bonferroni-Dunn′s,Holm′s,and Hochberg′s procedures for OBL-μTLBO and micro-population algorithms

3.2 与非微种群算法的比较

在本实验中，OBL-μTLBO算法与4种非微种群算法的性能进行比较。期望求解精度同3.1节。标准TLBO算法的种群规模设定为30；TLBO-CSWL算法的种群规模设定为40；FSADE算法和Rcr-JADE-s4的种群规模分别设定为50和100，算法参数设置均与文献[6]一致，结果见表4。从表4可以看出，OBL-μTLBO算法在f1、f2、f3、f4、f6、f7、f9、f10、f11上的平均评价次数均明显少于所有比较算法，这说明所提方法具有较快的收敛速度。而在函数f5、f8、f13上，Rcr-JADE-s4算法的实验结果要优于本文的OBL-μTLBO算法。这说明Rcr-JADE-s4算法在这3个函数上具有较快的收敛速度。统计分析结果见表5和表6。由表5可知，笔者所提算法与非微种群算法相比，OBL-μTLBO同样具有较高的搜索效率。从表6可以看出，OBL-μTLBO算法的搜索效率要明显优于其他所有比较的非微种群算法。

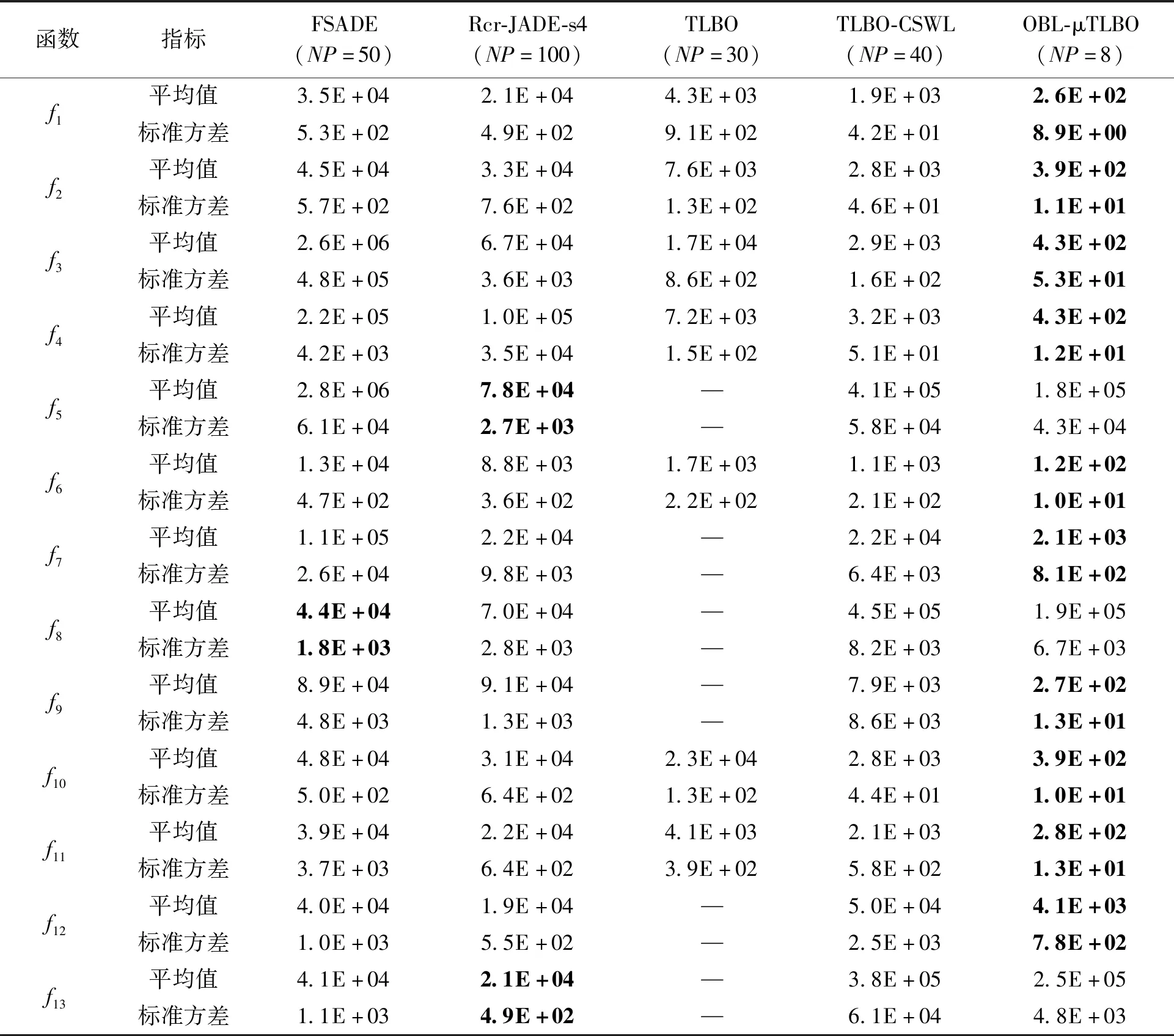
表4 OBL-μTLBO算法与非微种群算法的结果Table 4 Experimental results of the OBL-μTLBO algorithm and non-micro-population algorithms

表5 Friedman测试在OBL-μTLBO和非微种群算法上所得排序结果Table 5 Ranking obtained by Friedman′s test for OBL-μTLBO and non-micro-population algorithms

表6 Bonferroni-Dunn、Holm和Hochberg在OBL-μTLBO和非微种群算法上所得p值Table 6 p-values obtained by Bonferroni-Dunn′s,Holm′s,and Hochberg′s procedures for OBL-μTLBOand non-micro-population algorithms

3.3 OBL-μTLBO与μJADE、TLBO-CSWL、ODE的比较

为进一步验证OBL-μTLBO算法的寻优性能，本部分将对OBL-μTLBO算法与表现较好的微种群算法μJADE和非微种群算法TLBO-CSWL、ODE进行性能比较。与3.1和3.2节不同，在本实验中，所有算法终止条件设定为最大的适应度函数评价次数，即30 000。同时，μJADE、ODE、TLBO-CSWL的种群规模分别设定为8、100、40。所得结果见表7。从表7可以看出,OBL-μTLBO 算法在f1、f2、f3、f4、f5、f6、f7、f9、f10、f11、f12上得到的平均结果明显优于μJADE算法。而μJADE只在f8和f13这两个函数上要比所提算法表现得好。这足以说明OBL-μTLBO算法的寻优效率要好于μJADE算法。相比于TLBO-CSWL，除测试函数f7、f8、f12外，OBL-μTLBO算法在所有函数上都要比它表现得好。此外，OBL-μTLBO算法在所有测试函数上的优化结果都要好于ODE。综上，OBL-μTLBO算法不仅具有较快的收敛速度和能够降低计算内存的要求，而且还有较强的全局搜索能力。

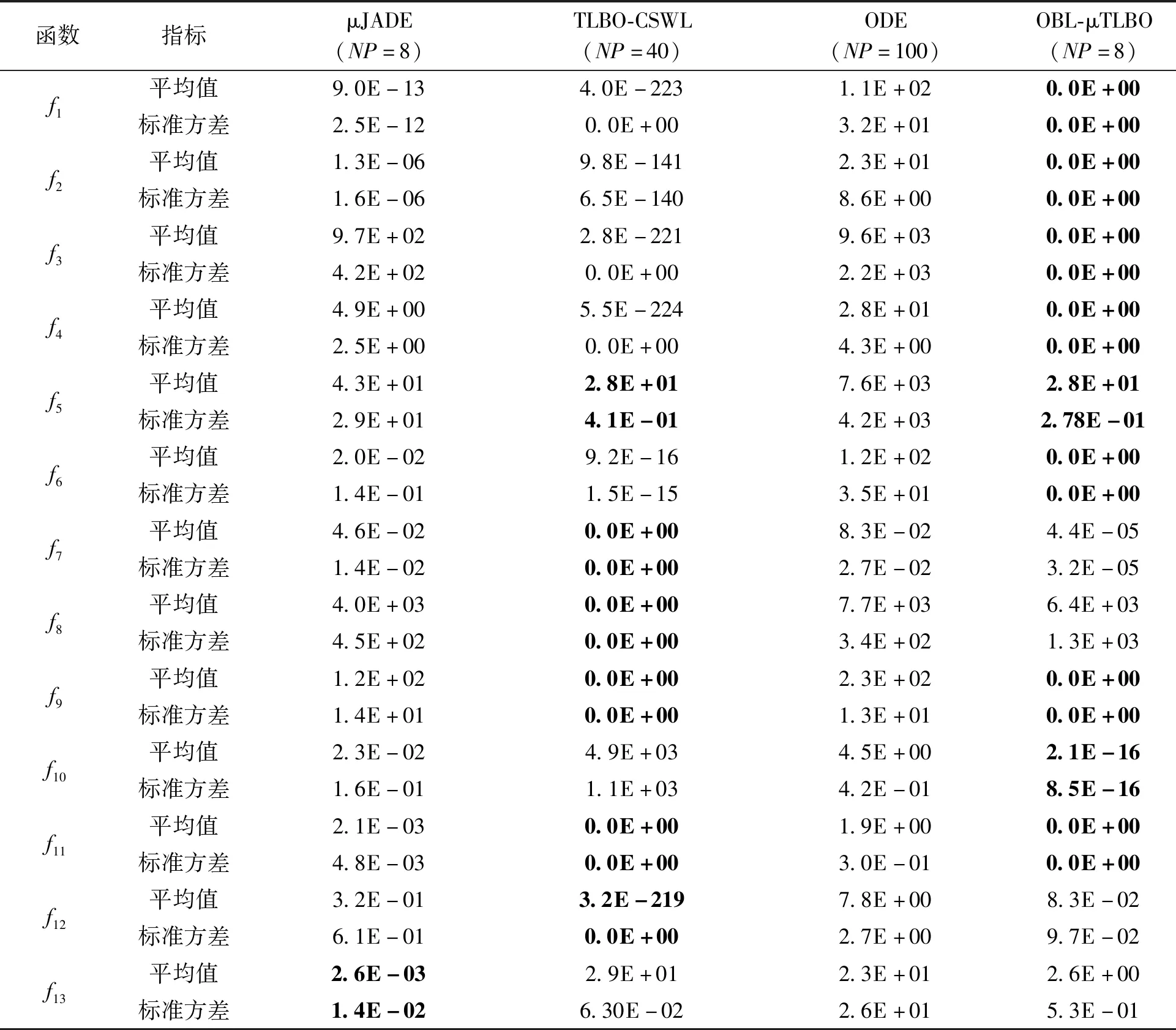
表7 所有比较算法30维仿真测试结果Table 7 Experimental results on all Comparison algorithms with 30 D

为得到可靠结论，3种非参数统计分析方法被用来对所有比较算法的平均值进行统计分析，其结果见表8。由表8可知，OBL-μTLBO算法的性能要明显优于μJADE和ODE。另外，虽然OBL-μTLBO算法和TLBO-CSWL算法的性能在统计学意义上不存在显著性的差异，但是从表7中的结果可知，OBL-μTLBO算法的整体性能要优于TLBO-CSWL算法。

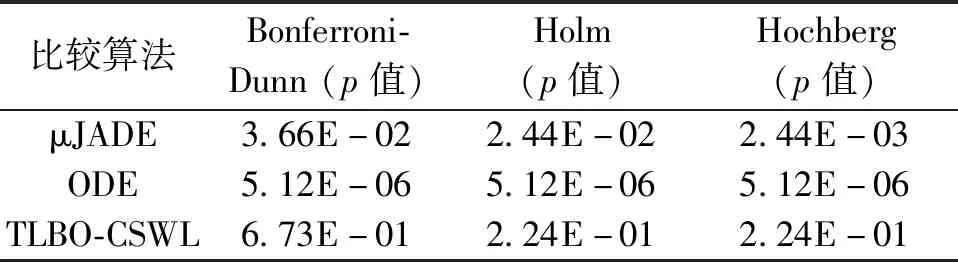
表8 Bonferroni-Dunn、Holm在OBL-μTLBO和其他3种算法上所得p值Table 8 p-values obtained by Bonferroni-Dunn′s,Holm′s,and Hochberg′s procedures for OBL-μTLBO and three algorithms

3.4 种群规模的敏感性分析

本部分对OBL-μTLBO算法的种群规模进行敏感性分析。其种群规模分别设定为5、8、10、15、20、30、40、50、100。对于每个测试函数，算法终止条件设定为最大适应度函数评价次数30 000,并使用13个30维的测试函数来对不同的种群规模进行分析。同时,Friedman统计方法用来对实验结果进行统计分析，结果见表9。从表9可知，种群规模对OBL-μTLBO算法的性能没有显著影响。因此，算法使用者可以对OBL-μTLBO算法的种群规模进行方便设置。此外，从Friedman的排序结果(见图1)来看，在有限的计算资源且要保证算法良好寻优能力的情况下，较小的种群规模更有利于OBL-μTLBO算法的搜索。

表9 OBL-μTLBO算法的种群规模敏感性分析Table 9 Sensitivity analysis to population size of OBL-μTLBO

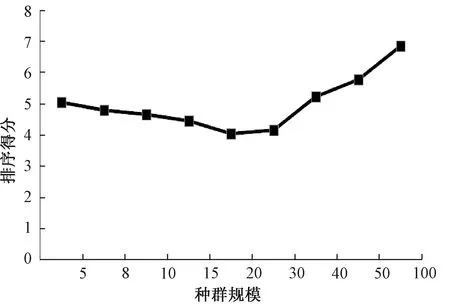
图1 Friedman 测试排序结果Figure 1 Ranking obtained by Friedman′s test

4 OBL-μTLBO算法在非合作博弈问题中的应用

4.1 博弈问题描述

假设有n个局中人参与博弈，所有局中人策略构成一个策略组合(strategy profile)，如果某情况下无一参与者可以独自行动而增加收益(即为了自身利益的最大化，没有任何单独的一方愿意改变其策略)，此时博弈模型处于稳定的状态，此策略组合被称为纳什均衡。参考文献[13]中的问题描述，对于两人有限非合作博弈问题：设局中人1的混合策略x=(x1,x2,…,xm)，局中人2的混合策略y=(y1,y2,…,yn)。Am×n、Bm×n分别为局中人1和局中人2的支付矩阵，则局中人1和局中人2的期望支付分别为xAyT和xByT。其中，(x*,y*)为双矩阵博弈问题的一个纳什均衡解的充分必要条件为：

(7)

算法中的每个个体的取值表示所有局中人的混合策略，则双矩阵博弈问题z=(x,y)的适应度函数可以表示为：

(8)

式中：Ai表示Am×n的第i行；Bj表示Bm×n的第j列。

根据纳什均衡的定义和性质[10]可知，混合局势z*=(x*，y*)为双矩阵博弈问题的一个纳什均衡解的充分必要条件为：存在z*=(x*，y*)，使得f(z*)=0，且对于任意的z≠z*，都有f(z)>0。

4.2 案例研究

选取两个双矩阵博弈问题[26-27]。

例1：博弈模型1,Γ1≡(x1,y1;A1,B1)，支付矩阵如下：

该问题的唯一纳什均衡解为(1/3,1/3,1/3;1/3,1/3,1/3)。

例2：博弈模型2,Γ2≡(x2,y2;A2,B2)，支付矩阵如下：

该问题的唯一纳什均衡解为(0,0,1;0,0,1)。

为了验证微种群算法OBL-μTLBO求解非合作博弈纳什均衡问题的有效性，将OBL-μTLBO算法和测试中性能较好的TLBO-CSWL[19]算法应用于求解以上两个3维双矩阵博弈问题，并与其他几种知名算法jDE[28]、SaDE[29]、CLPSO[30]进行性能比较。其中OBL-μTLBO 的种群规模设定为8，而其余所有对比算法的参数设定均与对比文献[6]一致。求解结果使用Wilcoxon秩和检验[31]

所有算法的求解结果(平均值和标准方差，括号内是标准方差)以及统计分析结果见表10。从表10中可以看出，OBL-μTLBO 算法在两个博弈实例上所得平均值均要好于所比较算法。表11和表12为所有算法在算例1和算例2上得到的最好结果。从表11和12可以看出，OBL-μTLBO算法在两个算法上均可以取得最优的纳什均衡解，且求解的适应度函数精度明显优于jDE、SaDE、CLPSO以及TLBO-CSWL算法。

表10 所有算法在博弈问题上得到的实验结果Table 10 Experimental results of all algorithms on game problems

表11 所有算法在博弈算例1上得到的最好结果Table 11 The best experimental results of all algorithms on game problem 1

表12 所有算法在博弈算例2上得到的最好结果Table 12 The best experimental results of all algorithms on game problem 2

以上分析结果表明，所提出的OBL-μTLBO算法能够有效地求解非合作博弈纳什均衡问题。

5 结论

为平衡微种群教与学优化算法的全局和局部搜索能力，笔者提出了OBL-μTLBO算法。在该算法中，利用微种群来提高教与学优化算法的收敛速率，且在教学阶段加入了反向学习来指导种群进化，使算法具备反向学习的能力，提高了算法的全局探索能力。OBL-μTLBO算法跟μJADE、DESP、MDEVM、MDEVM-Fajfar等微种群算法和FSADE、Rcr-JADE-s4、TLBO、TLBO-CSWL、ODE等非微种群算法进行性能比较，结果表明，OBL-μTLBO算法的整体性能在所有比较算法中是最好的。因此，反向学习策略对于提升微种群算法的优化性能是有效的。另外，对OBL-μTLBO算法的种群规模进行敏感性分析。统计分析结果表明，OBL-μTLBO算法的性能不受种群大小影响,但在有限计算资源下，小的种群规模更有利于其搜索。最后，将OBL-μTLBO算法应用到非合作博弈问题，仿真结果表明，所提OBL-μTLBO算法能够取得较好的优化结果。