不同测风时长的数据插补对风能参数的影响研究
2020-10-10付淑仪
文 | 付淑仪
全面实现平价上网政策的出台,引发业内的“抢装潮”。为占得先机,投资者们一方面抓紧推进已核准项目的开工建设,另一方面,加快寻找可能的资源并上报核准。按照NB/T31147―2018《风电场工程风能资源测量与评估技术规范》的要求,进行详细的风能资源评估至少需要1个完整年的测风数据。但实际上,投资者们无法按部就班等到立塔1年后再进行投资决策。因此,由于测风时长不够而带来的风能资源评估误差是显而易见的。
本文选取两座测风塔为目标塔(对应的参照塔分别为三座和两座),研究在目标塔实测时长不满1年的情况下,与目标塔具有不同相关性的参照数据源以及不同线性回归插补方法的选取对目标塔风速、利用小时数等参数的影响,以期为行业投资提供参考。
测风塔概况
为了评估参照塔与目标塔之间数据相关性对结果的影响,本文以两个山地风电场为例进行介绍。
风电场A选取目标塔M1以及参照塔C11、C12、C13,测风时段为2015年9月1日―2016年8月31日,依据规范判断所有测风塔在选取的时间段内10min有效数据完整率皆高于94%,主风向为NNE。三座参照塔距离M1分别为8.5km(东南)、12.5km(东南)、7km(西北),所在区域皆为丘陵低山,山脊较为宽阔,下垫面植被为1~2m低矮灌木丛。
风电场B选取目标塔M2以及参照塔C21、C22,测风时段为2016年7月1日-2017年6月30日,依据规范判断所有测风塔在选取的时间段内10min有效数据完整率皆高于99%,主风向以NNE为主。两座参照塔距离M2分别为6km(西北)、3.7km(西北),所在区域皆为高山,整体山势较为平缓,下垫面植被以松树为主。其中,C22与M2在同一条连续的山脊上。
研究方法
选定测风已满1年的测风塔作为目标测风塔,分别选取其前1个月、2个月……11个月的实测数据,采用另一座参照测风塔对其进行测风数据的延长插补,最终形成1个完整年的测风数据。将其与目标塔实测的1个完整年测风数据进行对比分析。本次分别采用总体相关法和分风向相关法两种不同的线性回归法进行目标测风塔风速的延长插补。
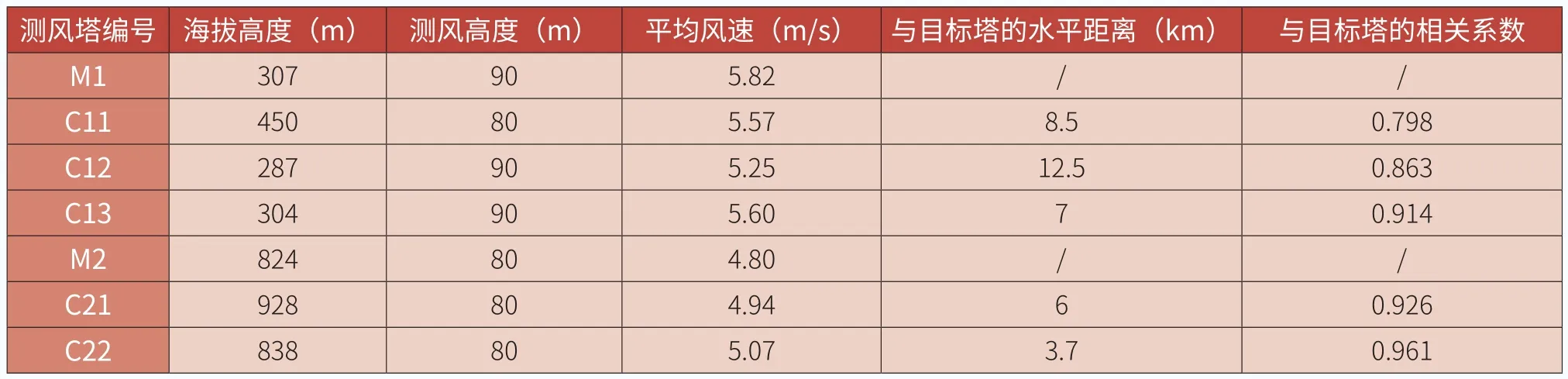
表1 测风塔信息
一、总体相关法
利用目标塔与参照塔同期的所有测风数据,分别建立不同测风时长下目标塔与参照塔风速数据的一元线性回归方程,利用该方程推算目标塔的缺测时间段风速。
以风电场A为例,目标塔M1与参照塔C11的同期测风时段为2015年年9月1日―2016年8月31日。分别对M1不同测风时长下的测风数据与C11同期数据进行相关性分析,建立总体相关方程,进而利用C11的实测数据对M1的缺测数据进行插补,最终形成11组满1个完整年的测风数据。表2列出不同测风时长下两塔之间的相关系数及总体相关方程。从表2中可以看出,当M1测风时长不满3个月时,目标塔与参照塔之间的风速相关系数变化幅度较大;当测风时长为3~6个月时,两者之间的相关系数较低;当测风时长大于等于7个月时,两者之间的相关系数趋于稳定。
二、分风向相关法
将参照塔的风向数据平均分为16个扇区,分别建立不同测风时长下每个扇区的目标塔与参照塔风速数据的一元线性回归方程,最终形成11组满1个完整年的测风数据。表3给出了当目标塔M1的测风时长为6个月时,C11和M1在不同风向扇区内的相关系数及相关方程。

表2 总体相关法相关方程及相关系数
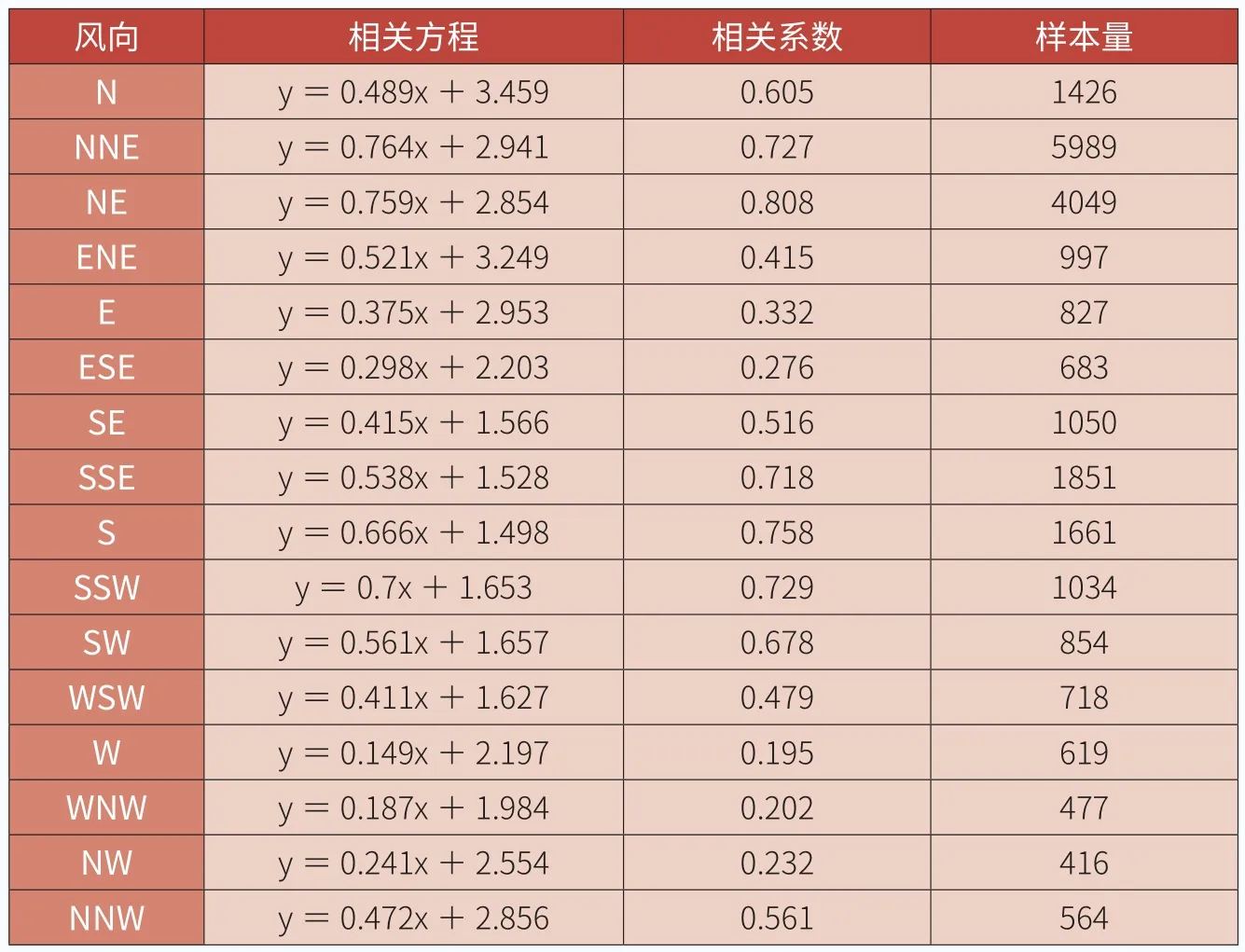
表3 分风向相关法相关方程及相关系数
三、年利用小时数计算
以WTG147-2500kW双馈型风电机组为例,其风轮直径为147m,单机容量为2500kW,切入风速为2.5m/s,切出风速为20m/s,是一款针对低风速区域开发的机型,功率曲线特性如表4所示。年利用小时数H的计算公式如式(1)所示,其中,理论发电量EN(单位:kWh/y)由法国美迪公司开发的Meteodyn WT软件模拟计算得到,折减系数R按经验值取值0.72,单机容量P为2500kW。
四、误差分析
为了对比不同计算条件下两种线性回归方法的插补精度,本文采用风速序列的平均绝对百分比误差平均风速的绝对误差以及年利用小时数的绝对误差AE(H)三个参数来进行评价。误差值越小,表示插补数据与实测数据的偏差越小。
如果Tr(t)代表t时刻的实测风速值,Es(t)代表由一元线性回归插补得到的t时刻的估算值,则将平均绝对百分比误差定义为式(2)。
如果X代表由实测风速序列计算得到的全年平均风速或年利用小时数,Y代表由插补后风速序列计算得到的全年平均风速或年利用小时数,则将绝对误差AE定义为式(3)。
结果分析
按照前述研究方法分别依据参照塔C11、C12和C13对M1进行数据插补,依据参照塔C21和C22对M2进行数据插补,共得到110组插补后的风速序列。考虑到当目标塔的测风时长不同时,需要插补的数据样本量不同,为了更好地对比两种方法的插补精确度,本文仅抽取2016年8月1日―2016年8月31日(M1)和2017年6月1日―2017年6月30日(M2)时间段内1个完整月的插补数据,进行风速平均绝对百分比误差对比,以此绘制图2。在此时间段内,110组插补后的风速序列样本量基本相同,且均为插补数据。表5、表6分别给出插补后各序列的平均风速值以及年利用小时数。图3、图4分别给出插补后各序列的平均风速绝对误差对比以及年利用小时数绝对误差对比。
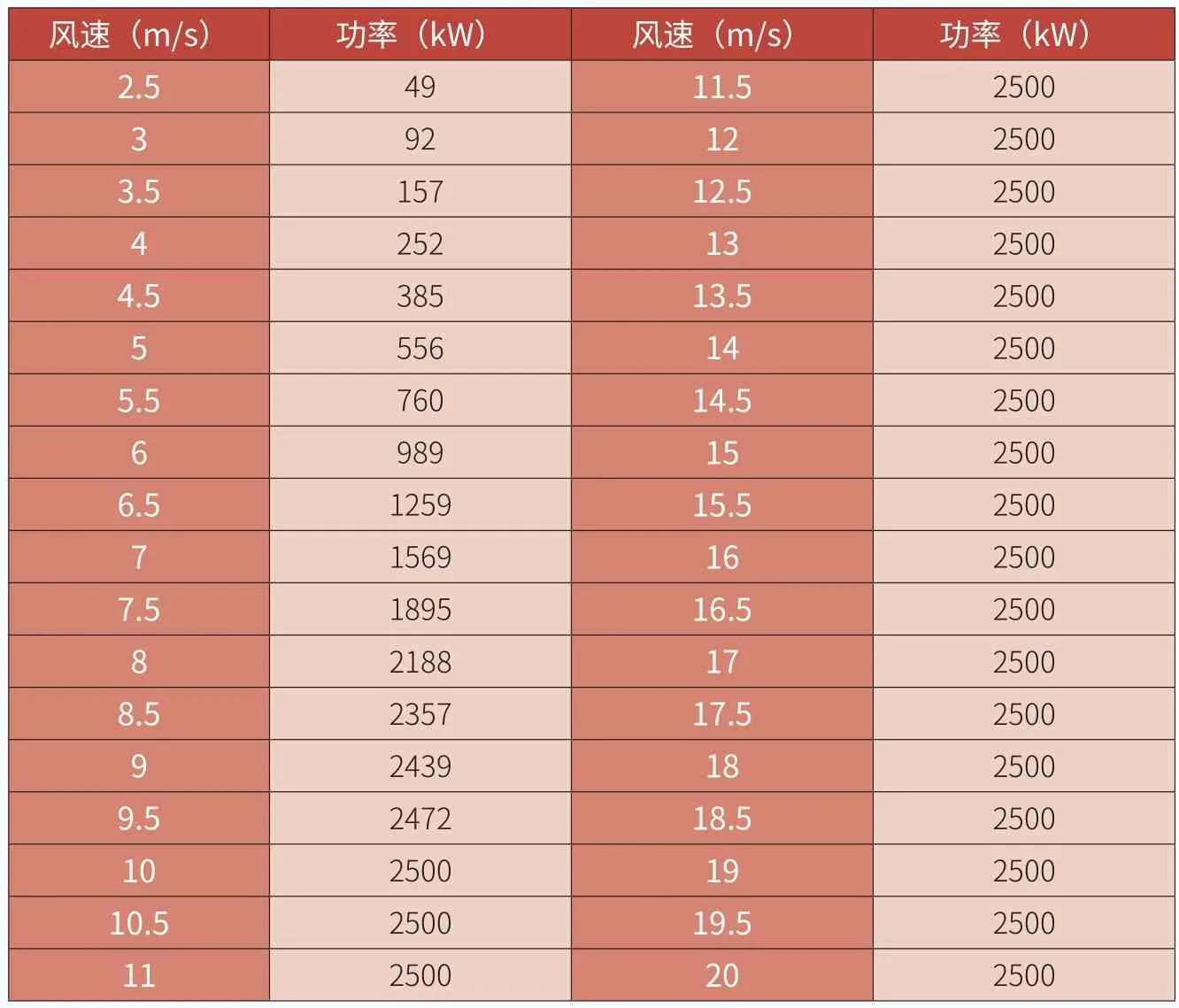
表4 机组功率曲线特性
从图2可以看出在同样的计算条件下,分风向相关法的精度总是高于总体相关法。随着参照塔与目标塔之间相关系数的提高,插补的平均绝对百分比误差随之减小,且两种数据插补方法得到的结果更接近;当两者的相关系数达到0.96时(对应图2中的C22两条曲线),两种数据插补方法得到的结果基本一致。当参照塔与目标塔之间的相关系数高于0.9时(对应图2中的C13、C21、C22共6条曲线),随着实际测风时长的增加,误差没有明显的起伏变化;当参照塔与目标塔之间的相关系数低于0.9时,随着实际测风时长的增加,误差呈现出先增大再减小的变化过程,对应表2列出的相关系数,可以推断插补后的风速序列平均绝对百分比误差与所选取的样本之间相关性呈相反的变化趋势。
表5、图3分别反映不同计算条件下的平均风速及其绝对误差对比。可以看出,当目标塔的实际测风时长在3个月及以下时,两种插补方法下的平均风速绝对误差波动范围较大;当实际测风时长满6个月时,平均风速绝对误差开始有下滑趋势。另外,当测风时长大于3个月时,采用分风向相关法插补后的平均风速绝对误差基本可以被控制在0.1m/s以内;采用总体相关法插补时,当参照塔与目标塔的相关系数小于0.9时,平均风速绝对误差大于0.1m/s。

表5 平均风速统计(m/s)
表6、图4分别反映不同计算条件下的年利用小时数及其绝对误差对比。可以看出,当目标塔的实际测风时长在3个月及以下时,两种插补方法下的年利用小时数绝对误差波动范围较大;当实际测风时长满6个月时,年利用小时数的绝对误差开始有下滑趋势。这与平均风速的变化规律基本一致。另外,对于风电场A,当测风时长大于6个月时,采用分风向相关法插补得到的年利用小时数绝对误差可被控制在50h以内;对于风电场B,当测风时长大于3个月时,采用分风向相关法插补得到的年利用小时数绝对误差可被控制在55h以内。若采用总体相关法,年利用小时数的绝对误差高于分风向相关法,随着参照塔与目标塔之间相关系数的提高,两者之间的差值减小,当相关系数提高到0.96时(对应于C22测风塔),两者基本相等。
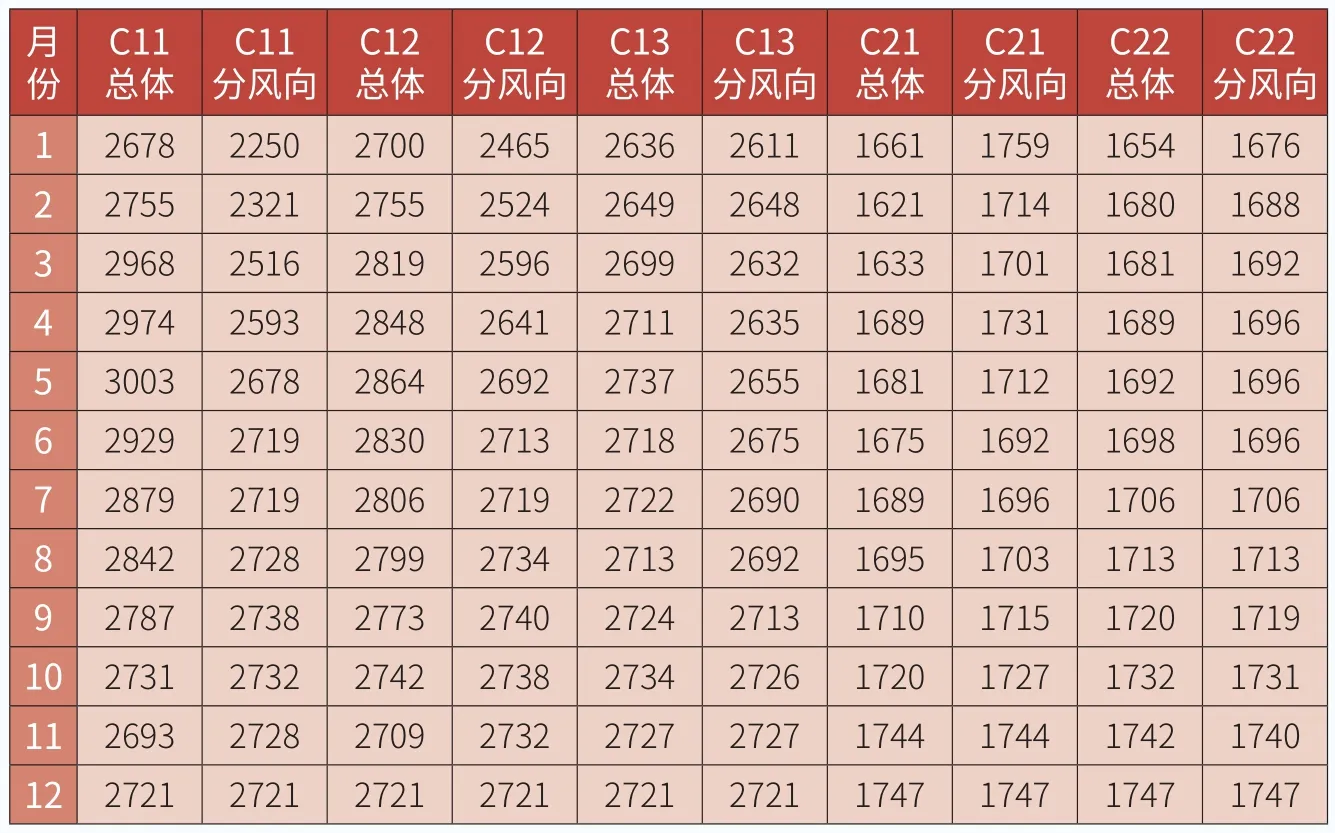
表6 年利用小时数统计(h)
结论
本文通过采用总体相关法和分风向相关法,利用不同的参照塔对不同测风时长下的目标塔进行延长插补,并分析相应的误差,得到以下结论:
从数据序列的角度来看,分风向相关法总是优于总体相关法。随着参照塔与目标塔之间相关系数的提高,误差减小,且两种线性回归法之间的差距也减小。
当参照塔与目标塔之间的相关系数为0.8~0.9时,采用分风向相关法可以将风能资源评估的测风时长缩短至6个月;当两者的相关系数高于0.9时,采用分风向相关法可以将风能资源评估的测风时长缩短至3个月。当测风时长在3个月以下时,插补得到的平均风速和年利用小时数误差较大,不建议采用该数据进行风能资源评估。
