耐压门C形密封圈大间隙密封性能分析与结构优化

李 晟 朱学康 李光明 殷 洪 唐 敏 张志强

(1.武汉第二船舶设计研究所 湖北武汉 430205；2.武汉大学动力与机械学院 湖北武汉 430072)

耐压门作为水下潜器重要的承压部件，其密封性能直接影响潜器的承压能力和安全性问题，因此，对耐压门密封件的密封性能研究十分重要[1]。O形圈被广泛用于水下潜器、压力容器等的静密封[2-7]，为进一步提高耐压门密封性能，本文作者提出采用新型密封形式C形密封圈作为耐压门密封件，基于有限元法对C形密封圈密封性能进行仿真计算，校核了典型算例的密封性能，分析了密封圈截面几何参数对其大间隙工况密封性能的影响，根据分析结果优化了密封圈截面几何参数，提高了密封结构在预紧压缩和大间隙工况下的密封性能。

1 模型建立

1.1 有限元模型

耐压门密封结构由C形密封圈、密封槽和密封盖板组成，密封结构截面主要几何参数如图1所示。密封圈截面几何参数如下：开口半径r=3.5 mm，开口高度b=9.0 mm，高度c=14.0 mm，开口间隙d=3.5 mm，宽度B=20 mm，e=15 mm，削斜高度f=2.0 mm。

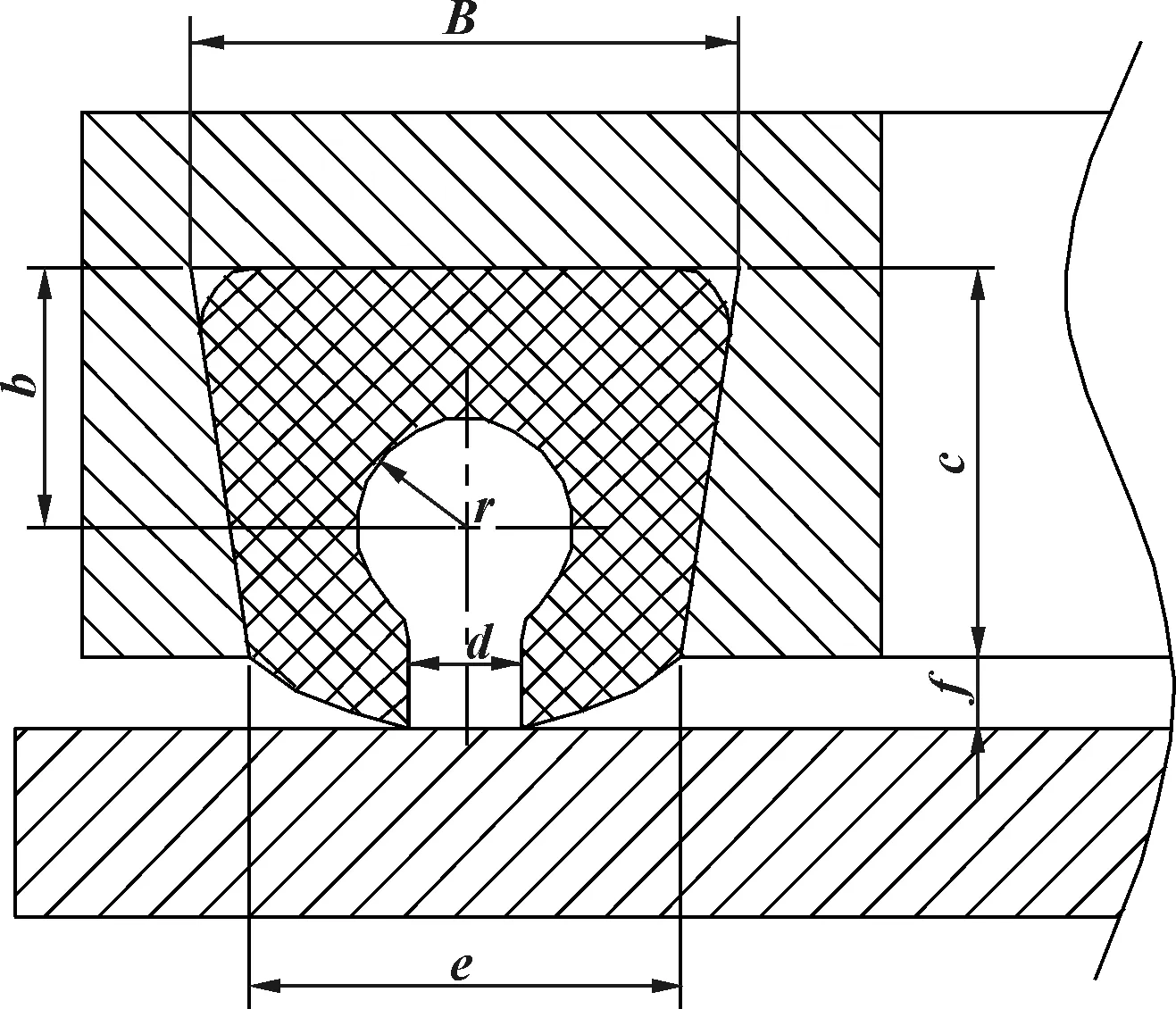
图1 耐压门密封结构截面几何参数示意

根据耐压门密封结构和受力边界条件特点，有限元计算时作如下假设[8-10]：

(1)密封槽与密封盖板均为钢结构，其刚度远大于橡胶材料，因此不考虑其变形，即将密封槽与盖板视为刚体；

(2)认为C形圈的橡胶材料为不可压缩材料，具有确定的弹性模量和泊松比；

(3)密封圈和密封槽轴向尺寸远大于横向尺寸，且轴向不存在偏心载荷，密封圈受力对称。

因此，有限元计算时将3D问题简化为平面应变问题进行分析，采用2D轴对称模型，建立其有限元模型如图2所示。

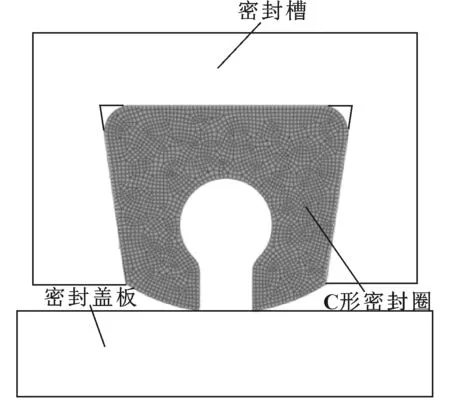
图2 C形密封结构有限元模型

1.2 材料参数

采用两参数Mooney-Rivlin模型[11-12]，则有

(1)

对于不可压缩材料，体积变化量很少，式(2)的最后一项可忽略不计。两参数Mooney-Rivlin模型可以用较少的参数来描述50%～150%应变范围内的变形，并得到比较高的精度，能够满足求解密封圈密封问题的需要。因此文中采用两参数Mooney-Rivlin模型来表征密封圈材料。根据实际橡胶试片力学测试结果，其材料Mooney-Rivlin常数c10=1.220 MPa，c01=0.024 MPa。

1.3 接触分析

有限元分析中接触算法有罚函数法、常规Lagrange法、增广Lagrange 法、法向Lagrange 法、切向罚函数法等，文中采用罚函数penalty模型，摩擦因数取为0.25[13]。

建立3个接触对，分别为密封圈与密封槽、密封圈与密封盖板、密封槽与密封盖板。

1.4 边界条件与载荷施加

计算载荷分为两步，第一步为预压，即约束上部的密封槽，对下部的密封盖板施加位移载荷至指定位移处，计算初始压缩条件下密封圈内部的应力分布以及密封圈与密封盖板间的接触应力。第二步是在预压后，对密封圈一侧及内部C形腔施加均布压力，模拟一侧有流体压力(2.0 MPa)，如图3所示。计算在一侧流体压力作用下密封圈内部的应力分布，以及密封圈与密封盖板连续界面上的接触应力。按照密封失效准则(式(2)和式(3))来判断密封圈的密封性能。

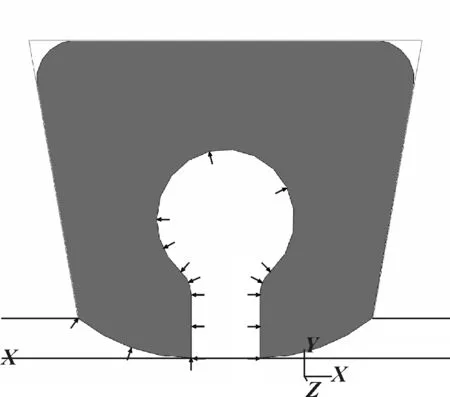
图3 流体载荷加载示意

1.5 密封失效准则

(1)最大接触应力准则[14-15]。根据密封理论，实现可靠密封的充分必要条件是密封圈与沟槽封盖连续界面上的接触应力不小于被密封压力，即

(σx)max≥p

(2)

实际上，密封圈在受压时沿密封界面的接触应力分布是非均匀的。尽管只要其应力峰值大于密封压力就可实现密封。但如果最大应力能有连续的密封带会使系统的密封性能更加可靠。

(2)剪切应力准则[16-17]。密封圈在沟槽转角处易产生应力集中，转角处的应力可达到兆帕数量级。如果该应力超过橡胶材料剪切强度时，则密封圈在此位置会被撕裂，甚至可能会被剪断，造成密封失效。因此，对剪切应力引起的密封失效问题也应予以考虑，密封下的剪切应力应满足

σxy<[τb]

(3)

式中：σxy为橡胶密封件在计算工况下所受的最大剪应力；[τb]为橡胶材料的许用抗剪强度。

2 典型算例计算结果及分析

在预紧压缩载荷作用下，密封圈内部的应力分布如图4(a)所示。最大应力分布在内部C形腔两侧，最大应力值为2.98 MPa。接触应力分布如图5(a)所示。可见在预紧压缩工况时接触应力较小，峰值为1.33 MPa。右下接触面的接触应力分布如图6(a)所示。密封圈内部的剪切应力如图7(a)所示。最大剪切应力出现在内部开口附近，峰值为1.14 MPa。

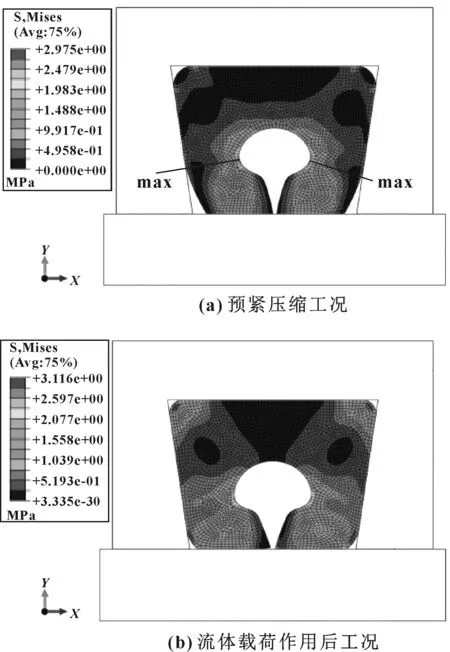
图4 密封圈内部应力分布

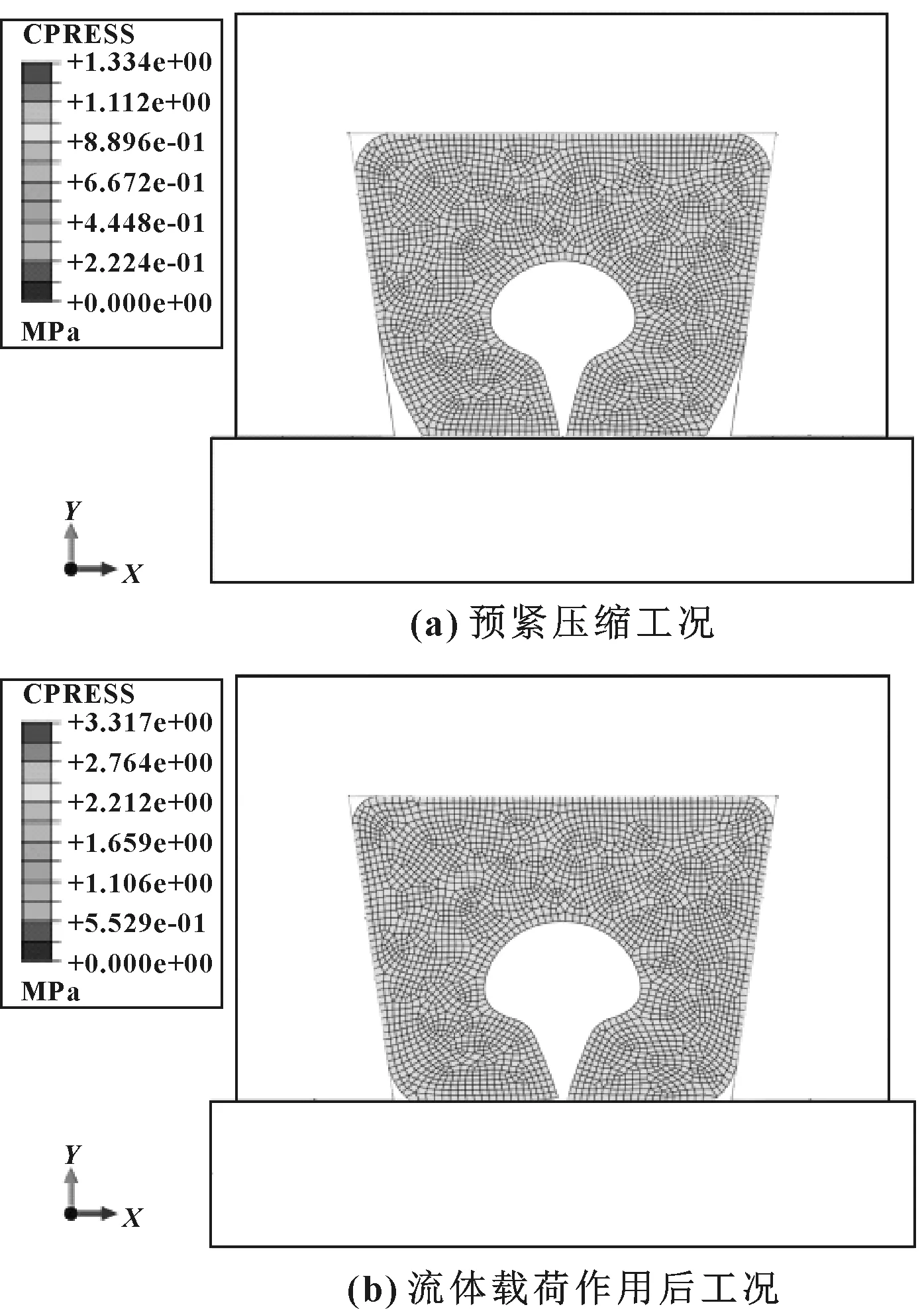
图5 接触应力分布

图6 右下接触面上的接触应力分布

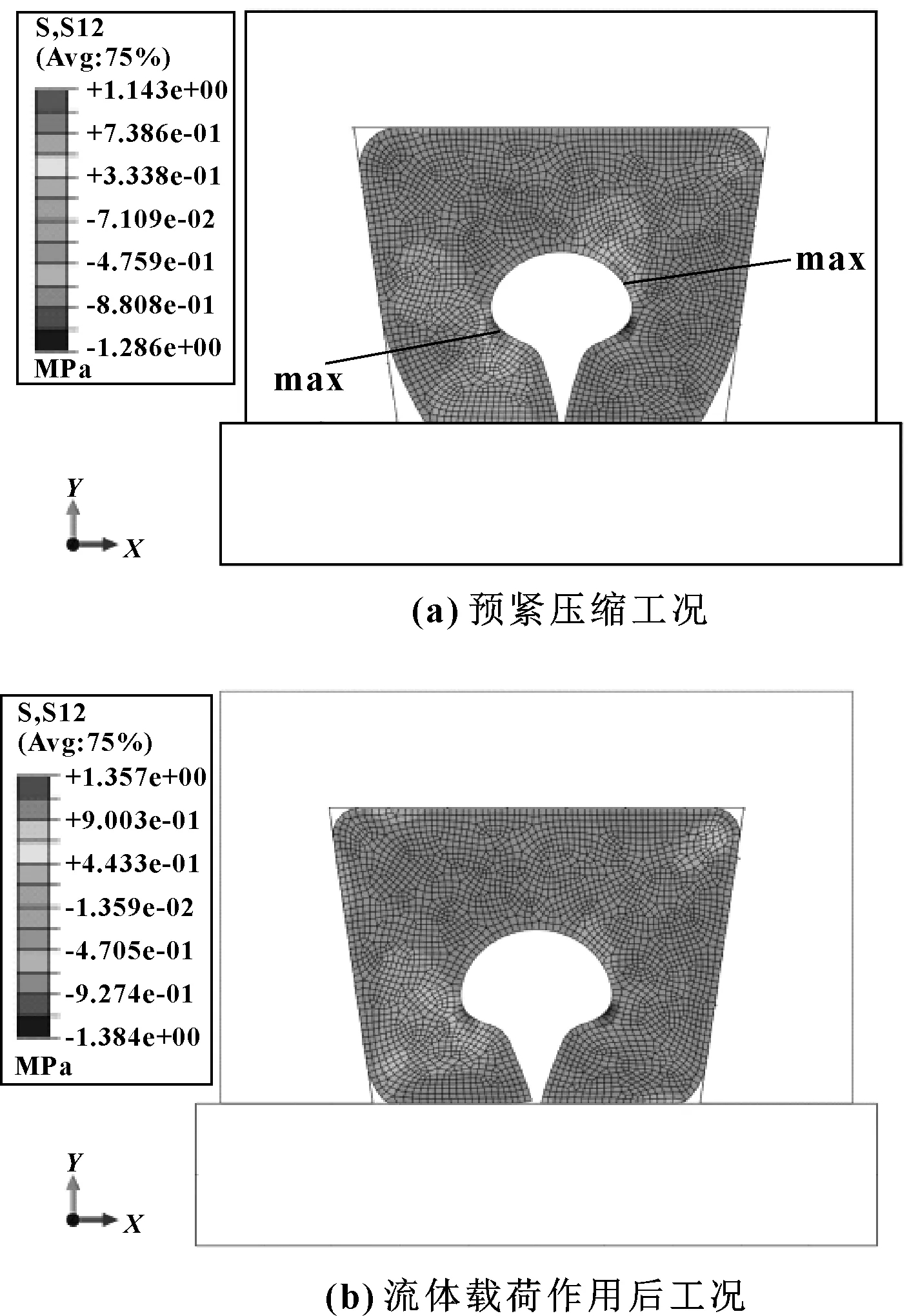
图7 剪应力分布

施加流体载荷作用后，密封圈内部应力分布如图4(b)所示，最大应力值为3.12 MPa，此时除C形腔两侧，在密封圈下接触面处的应力水平也较高。密封圈接触应力分布如图5(b)所示，最大接触应力为3.32 MPa，大于液体压力2.0 MPa。密封圈右下接触面上的接触应力分布如图6(b)所示，可见大于2.0 MPa的密封带长度有5.6 mm。考察最终的剪应力分布如图7(b)所示，最大剪应力为1.36 MPa。根据密封失效准则式(2)和式(3)，此时密封圈的密封性能是有保证的。

在计算过程中，随着流体载荷的加载，接触应力的峰值也随之增加，并始终大于流体载荷，可见此密封圈结构具有自密封特性。

3 分析与优化

3.1 截面几何参数对密封性能的影响

在流体作用下，盖板与密封槽结构间有可能产生间隙，对密封性能产生不利影响。为此有必要对有间隙工况下的密封性能进行仿真分析。在流体载荷p的作用下，上下封盖间出现间隙h。假设间隙h与流体载荷p呈线性关系，即p与h线性对应。当流体压力0.1 MPa时，间隙值h=0.1 mm；当最终流体载荷升至2 MPa，间隙值h=2.0 mm；此后，流体载荷保持2.0 MPa不变，间隙值继续扩大至4.5 mm。

为研究密封圈截面几何参数对其密封性能的影响，以图1给出的密封圈截面原始几何参数为基础，考察某一个几何参数为变量时，对大间隙工况下密封圈密封性能的影响。

3.1.1 开口半径r的影响

其他参数不变，调整开口半径r为2.3～3.8 mm，得到的预紧压缩接触应力分布如图8所示。可见，开口半径r越小，预紧压缩的峰值越高；开口半径为3.8 mm时，预紧压缩的峰值最小，但仍大于1.0 MPa，因而，初始密封的建立是能够保证的。

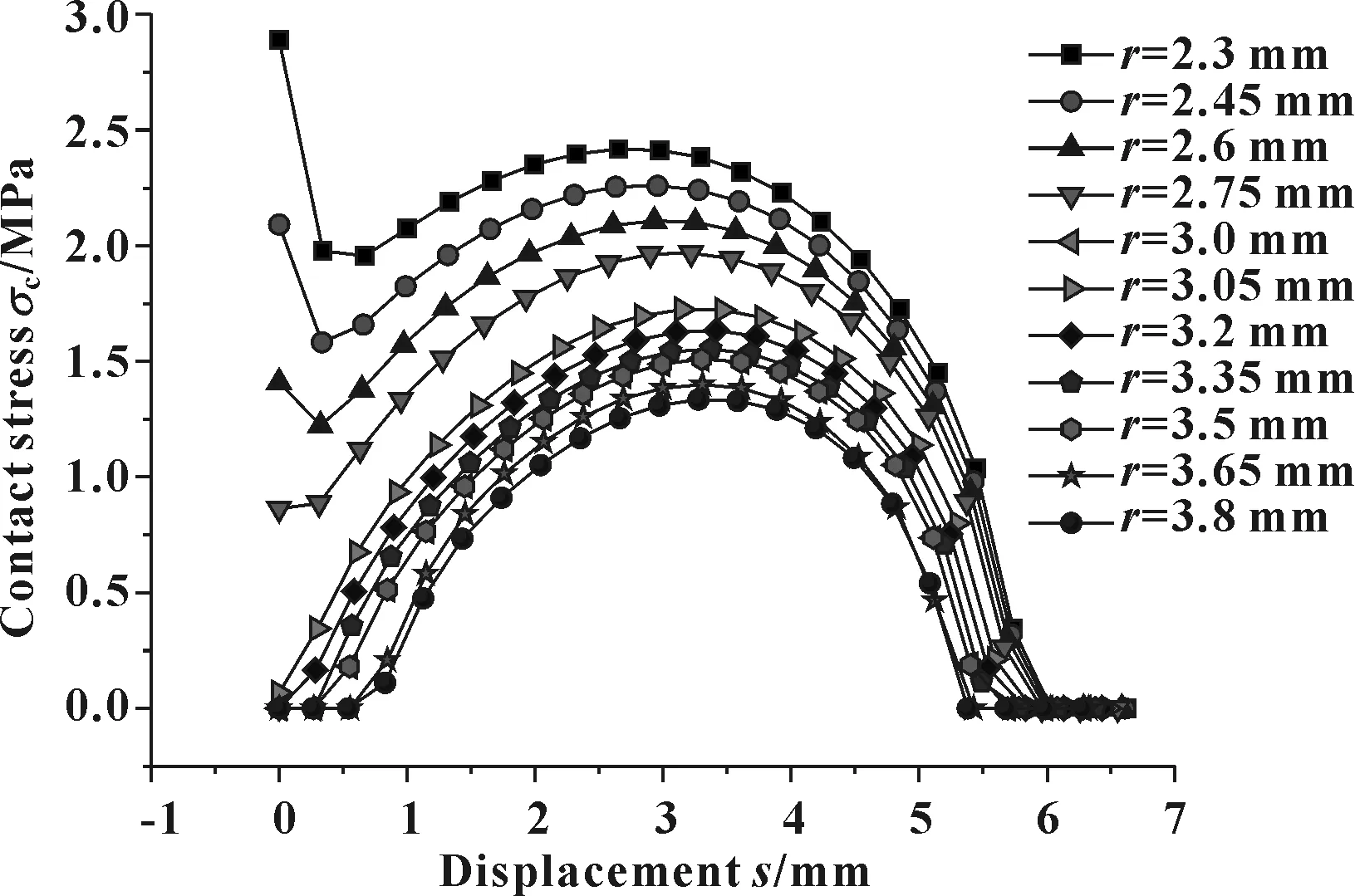
图8 不同r值时预紧压缩接触应力分布(无间隙)

开口半径r取不同值，间隙达到2 mm时，接触应力的分布如图9所示。可见开口半径r的改变，对2 mm间隙时的密封性能影响不大。

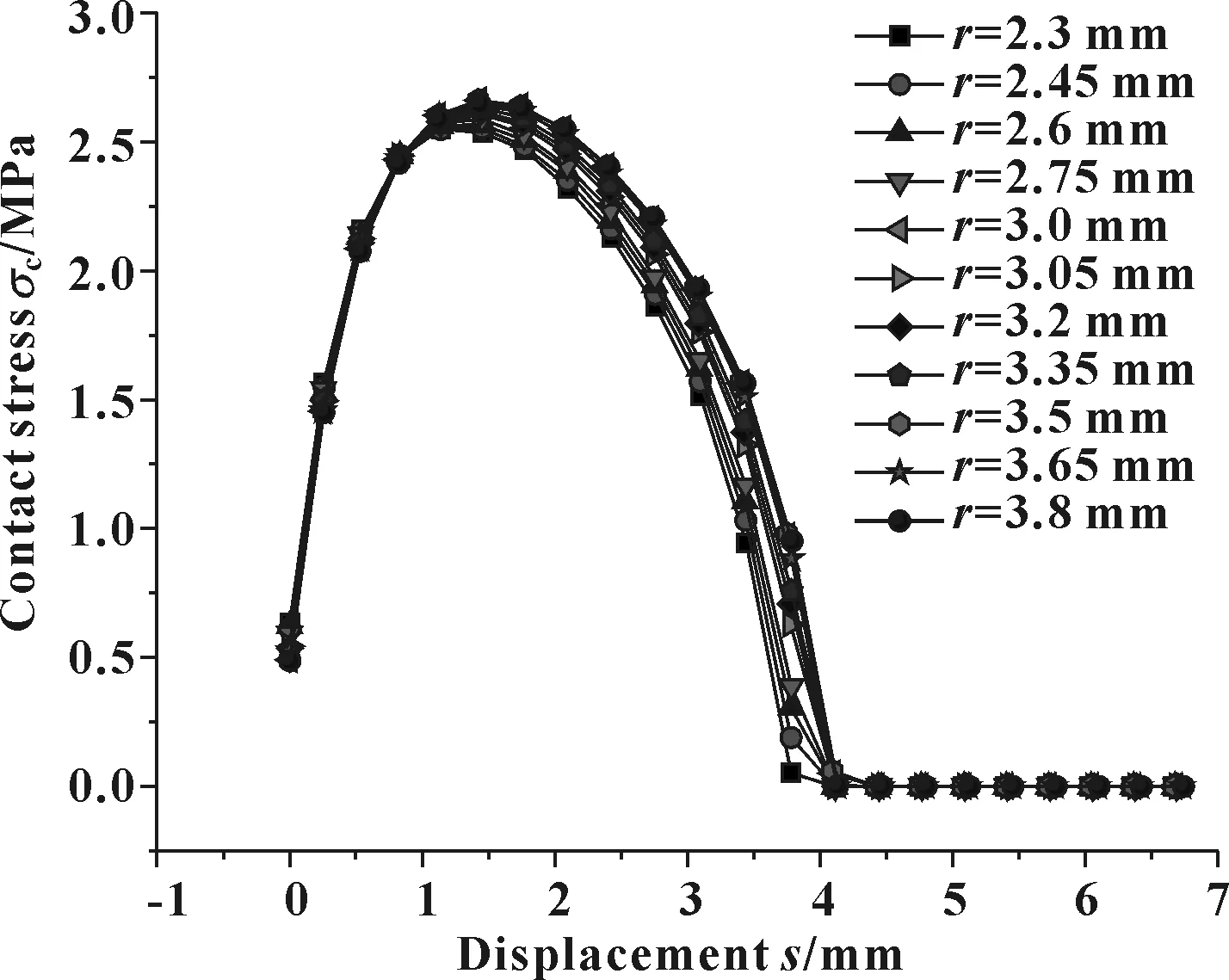
图9 不同r值及2 mm间隙时接触应力分布

开口半径r取不同值，间隙达到4.5 mm时，接触应力分布如图10所示，密封圈变形云图如图11所示，可见，r值越大，最大间隙时的密封带长度越大。

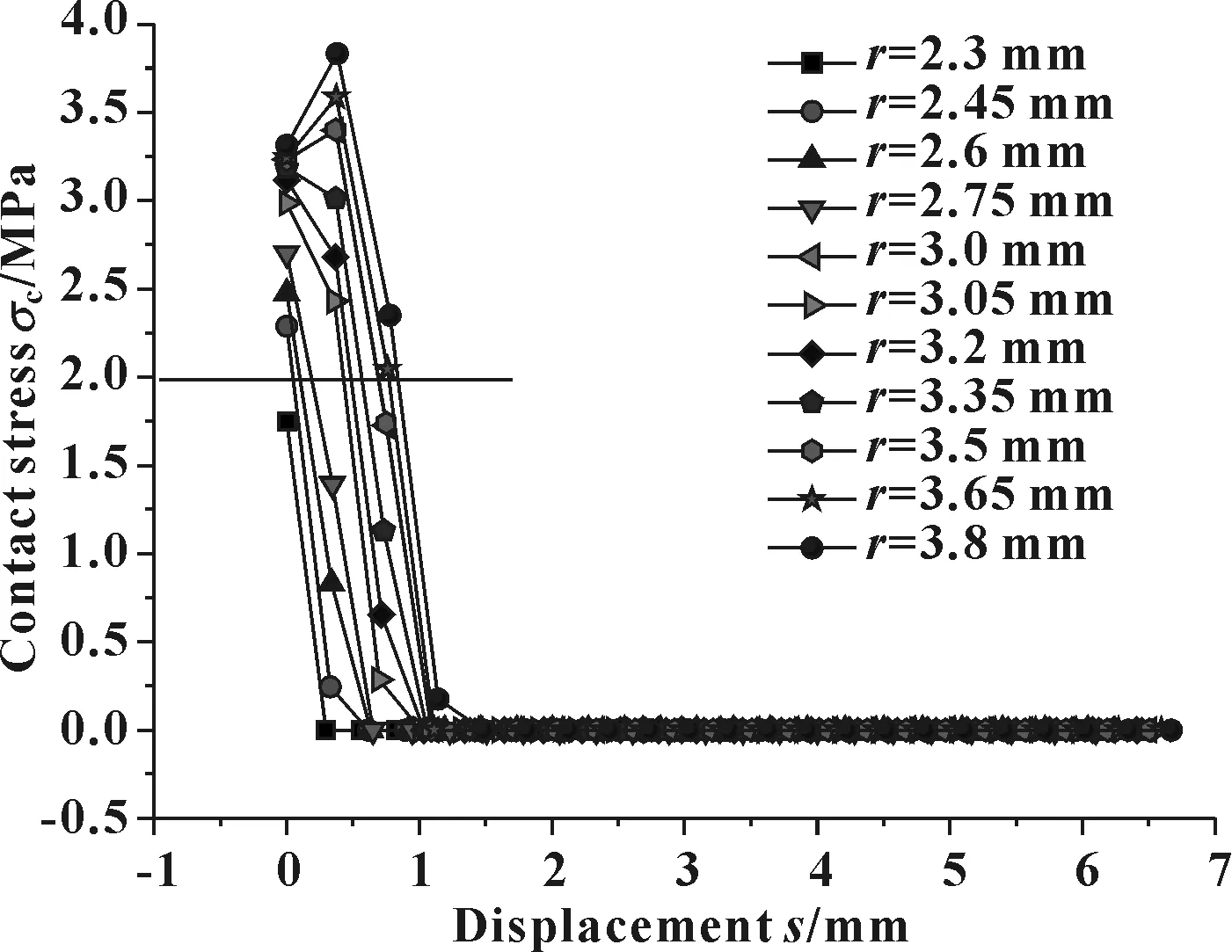
图10 不同r值及4.5 mm间隙时接触应力分布

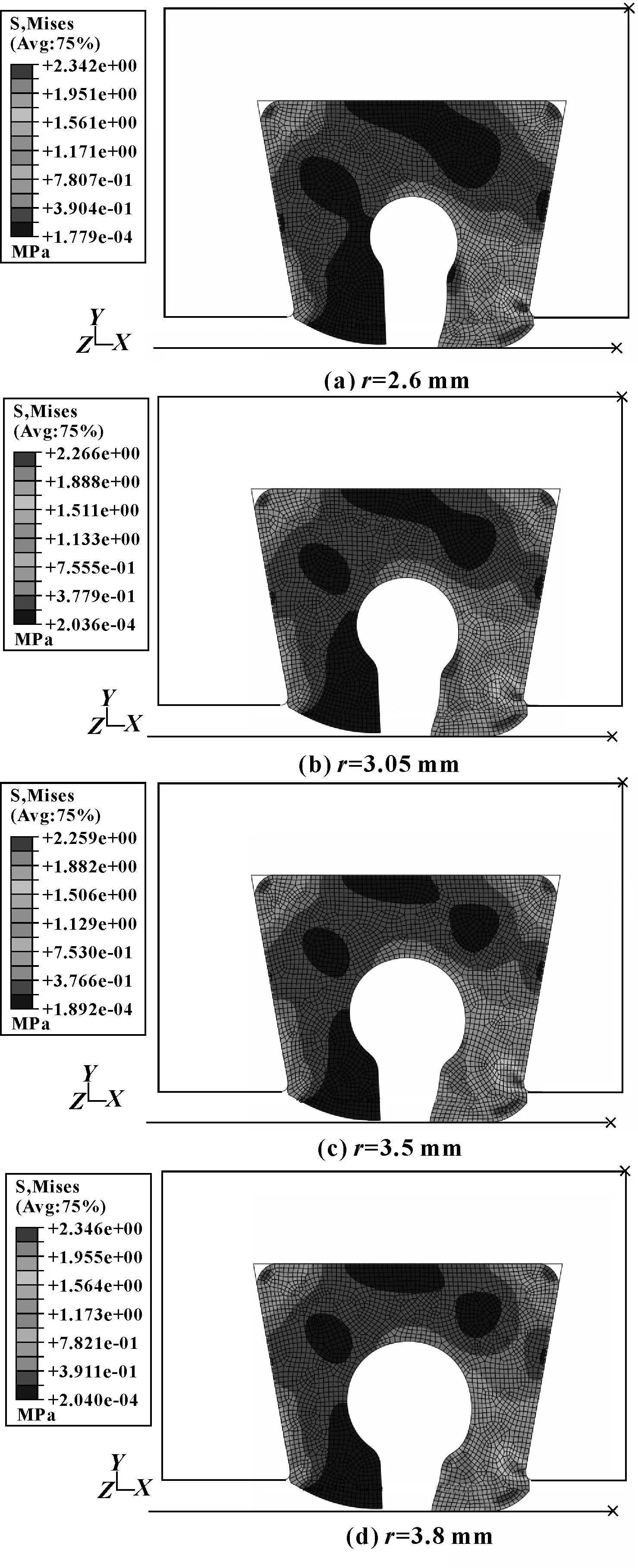
图11 不同r值及4.5 mm间隙时密封圈变形

开口半径r越大，则最大间隙时的密封性能越好。但r增大，预紧压缩时的密封性能降低。综合两方面的影响，合适的r值范围为3.0～3.5 mm。

3.1.2 几何参数b的影响

其他参数不变，调整开口高度b=7.0～11.5 mm，得到的预紧压缩接触应力分布如图12所示。可见，b值越大，预紧压缩应力峰值越高，b为7.0 mm时，预紧压缩应力峰值最小，但仍大于1.0 MPa，因而，初始密封的建立是能够保证的。

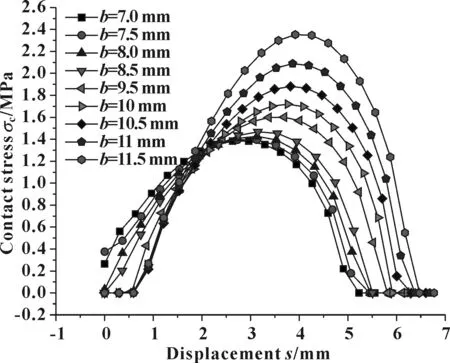
图12 不同b值时预紧压缩接触应力分布(无间隙)

开口高度b取不同值，间隙达到2 mm时，接触应力的分布如图13所示，可见b的改变，对2 mm间隙时的密封性能影响不大。开口高度b取不同值，间隙达到4.5 mm时，接触应力分布如图14所示，密封圈变形云图如图15所示。可见，b值对最大间隙时的密封带长度影响不大。

综合图12—15结果，开口高度b的值应大于8.5 mm。

图13 不同b值及2 mm间隙时接触应力分布

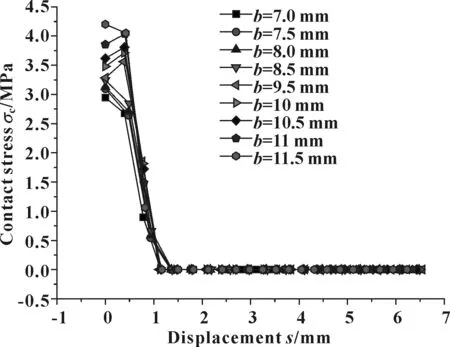
图14 不同b值及4.5 mm间隙时接触应力分布

3.1.3 几何参数c的影响

其他参数不变，调整高度c=11.5～15.5 mm，预紧压缩接触应力分布如图16所示。可见，c越小，预紧压缩应力峰值越高，c为15.5 mm时，预紧压缩应力峰值最小，但仍大于1.0 MPa，因而，初始密封的建立是能够保证的。

图16 不同c值时预紧压缩接触应力分布(无间隙)

高度c取不同值，间隙达到2 mm时，接触应力的分布如图17所示。可见c的改变，对2 mm间隙时的密封性能影响不大。

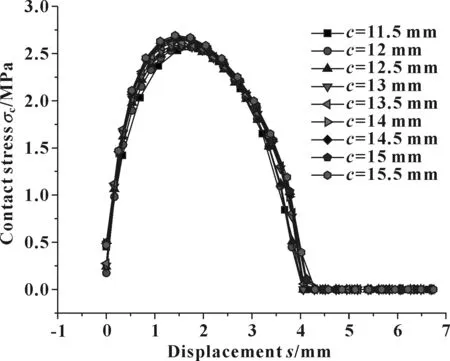
图17 不同c值及2 mm间隙时接触应力分布

高度c取不同值，间隙达到4.5 mm时，接触应力分布如图18所示，密封圈变形云图如图19所示。可见，c值对最大间隙时的密封带长度影响不大。

图18 不同c值及4.5 mm间隙时接触应力分布

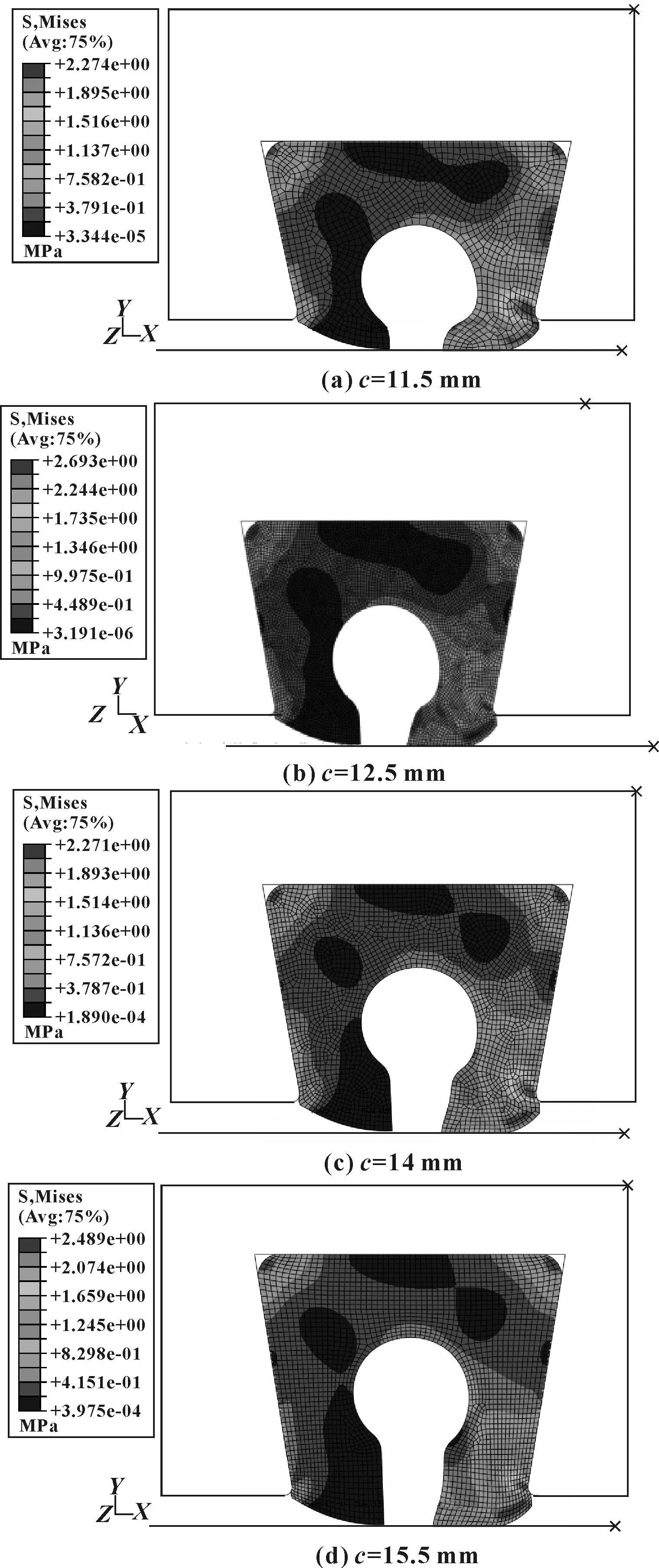
图19 不同c值及4.5 mm间隙时密封圈变形

3.1.4 几何参数d的影响

其他参数不变，调整开口间隙d=2～4 mm，不同d值时，预紧压缩接触应力分布如图20所示。可见，d的改变，对预紧压缩接触应力分布影响不大。

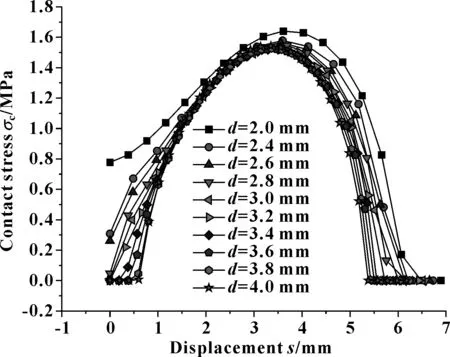
图20 不同d值时预紧压缩接触应力分布(无间隙)

开口间隙d取不同值，间隙达到2 mm时，接触应力的分布如图21所示。可见d的改变，对2 mm间隙时的密封性能影响不大。

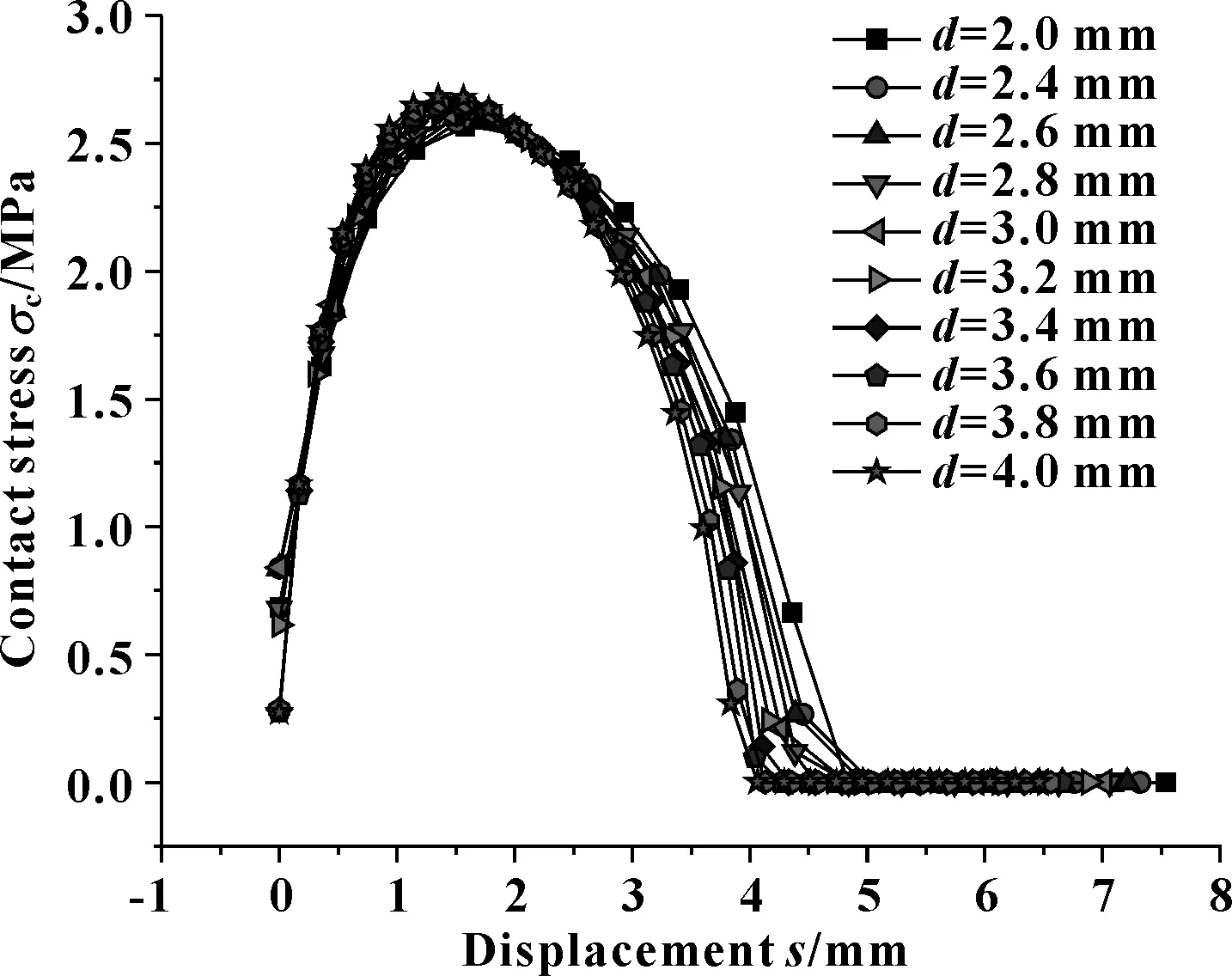
图21 不同d值及2 mm间隙时接触应力分布

开口间隙d取不同值，间隙达到4.5 mm时，接触应力分布如图22所示，密封圈变形云图如图23所示。可见，d值增大，4.5 mm间隙时的密封带长度减小。

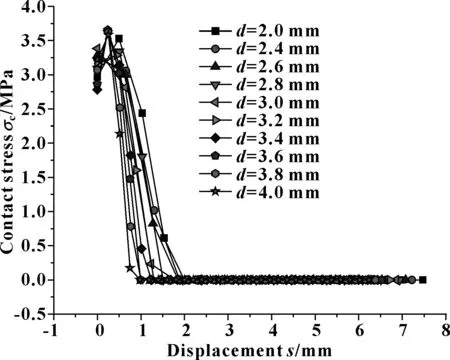
图22 不同d值及4.5 mm间隙时接触应力分布

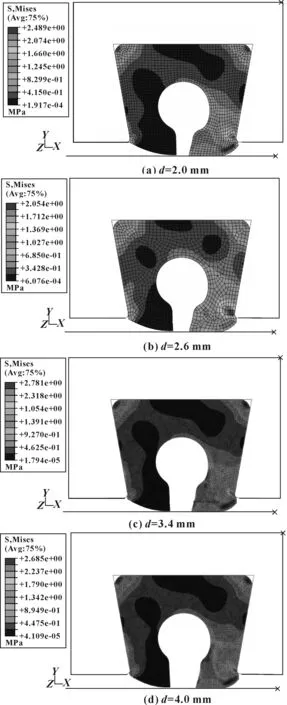
图23 不同d值及4.5 mm间隙时密封圈变形

3.1.5 几何参数e的影响

其他参数不变，调整宽度e=12.5～17.5 mm，得到，预紧压缩接触应力分布如图24所示。可见，e值增大，预紧压缩应力峰值增大，同时密封带的长度也增大。

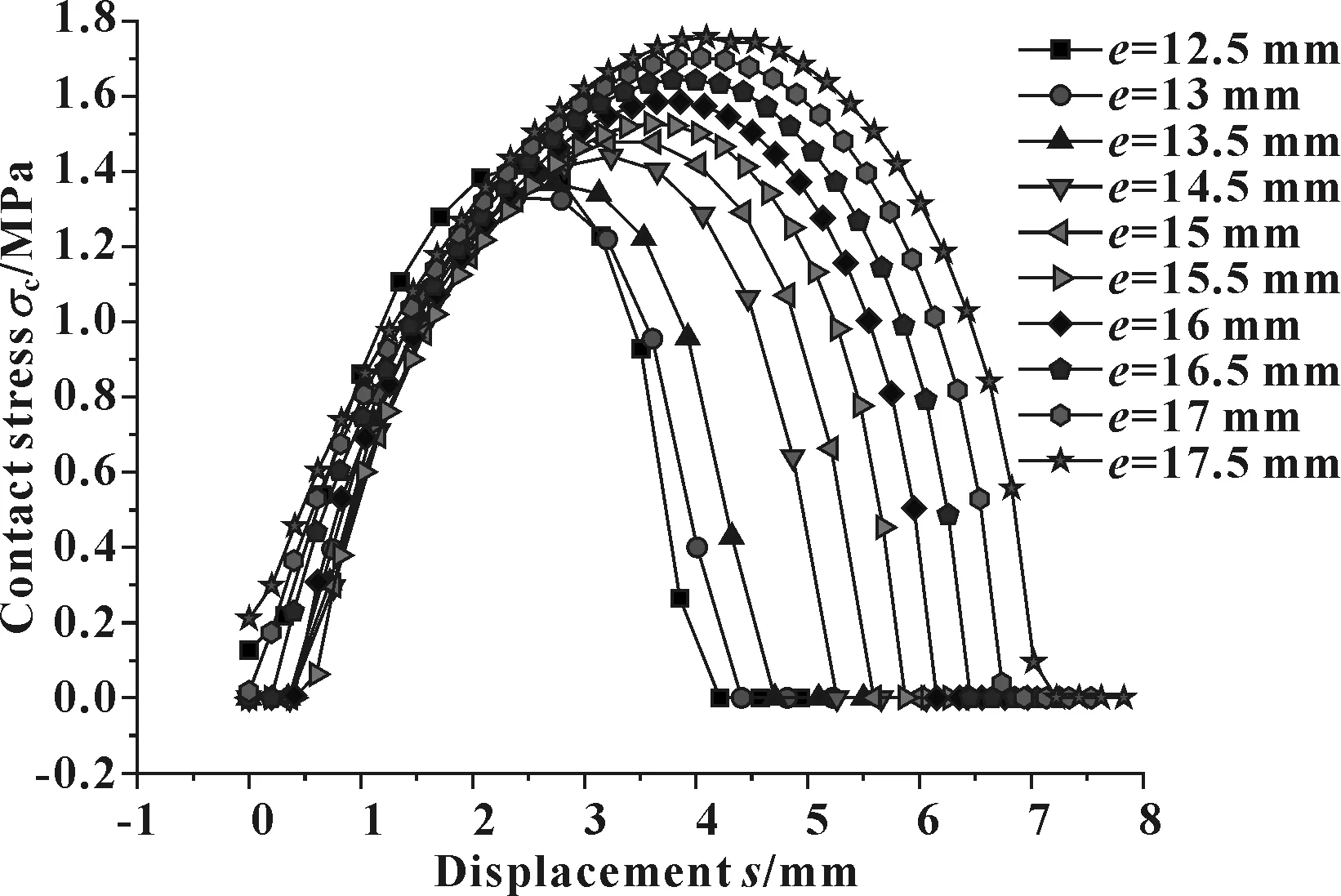
图24 不同e值时预紧压缩接触应力分布

宽度e取不同值，间隙达到2 mm时，接触应力的分布如图25所示。可见e值增大，使2 mm间隙时的接触应力峰值下降，而密封带长度增加。

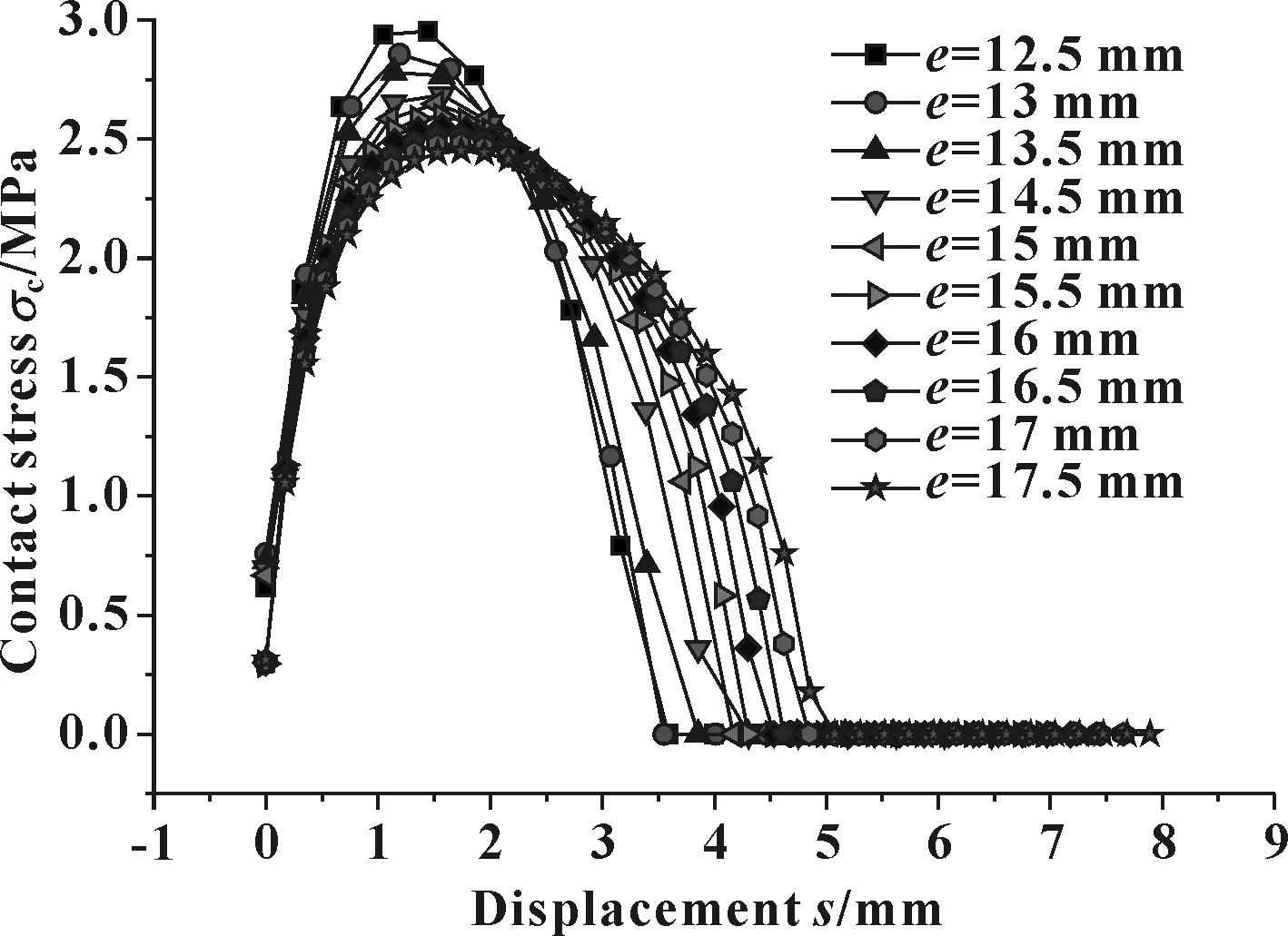
图25 不同e值及2 mm间隙接触应力分布

宽度e取不同值，间隙达到4.5 mm时，接触应力分布如图26所示，密封圈变形如图27所示。可见，e值为14.5 mm时，密封带长度最大，即最合适的e值为14.5 mm。

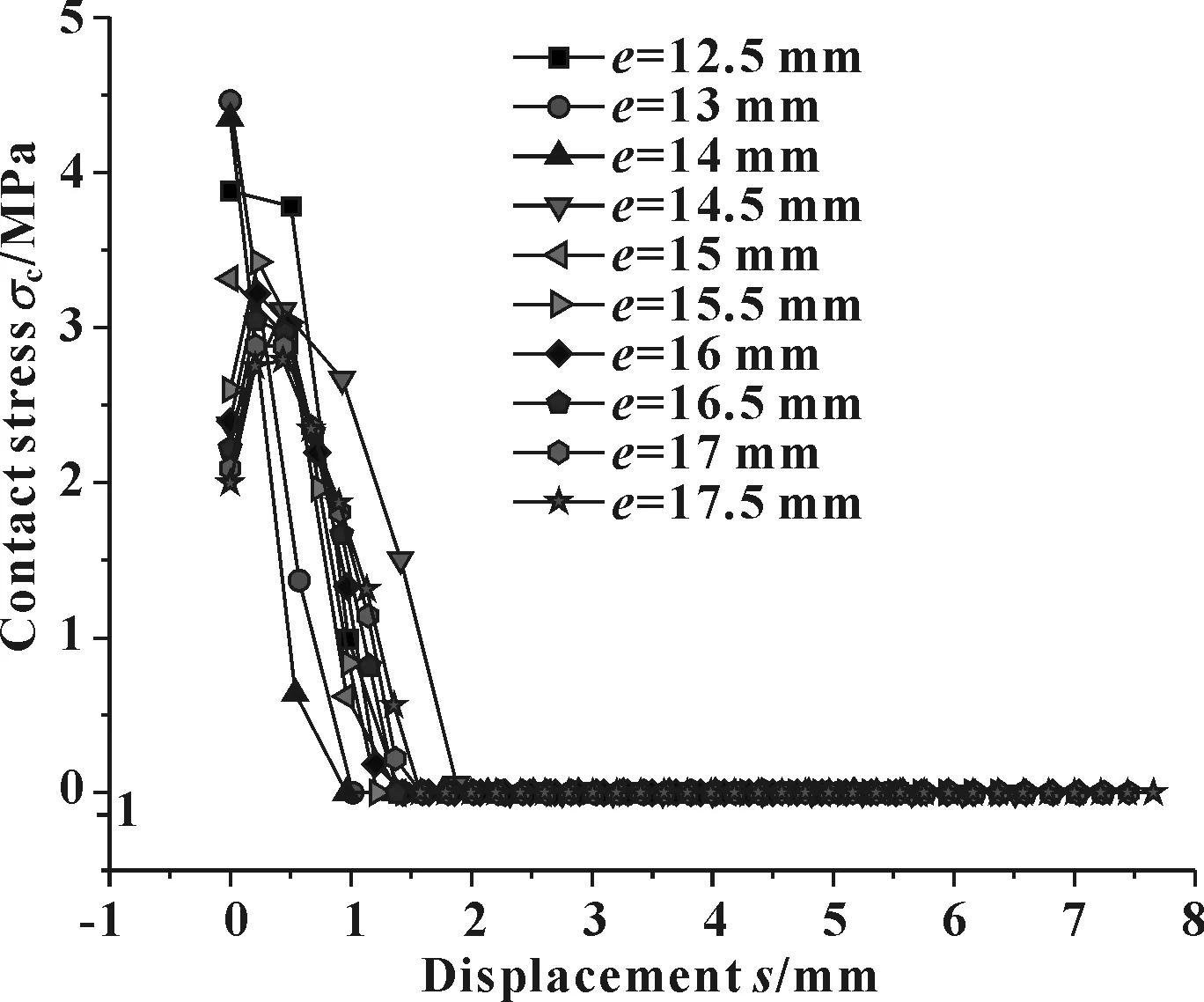
图26 不同e值及4.5 mm间隙时接触应力分布

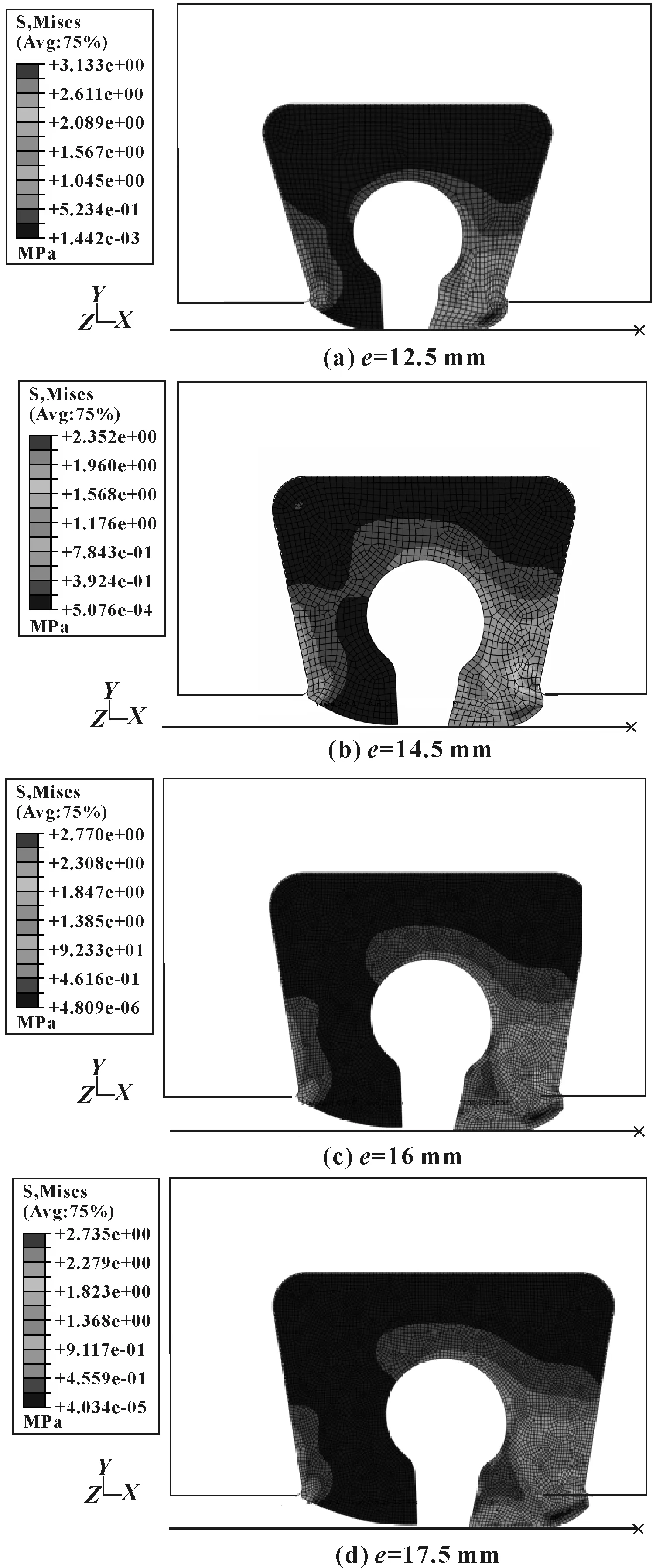
图27 不同e值及4.5 mm间隙时密封圈变形

3.1.6 几何参数f的影响

其他参数不变，调整削斜高度f=1.5～3.5 mm，得到预紧压缩接触应力分布如图28所示。可见，f值增大，预紧压缩的接触应力峰值增大，密封带长度也增大，预紧压缩的密封性能增大。

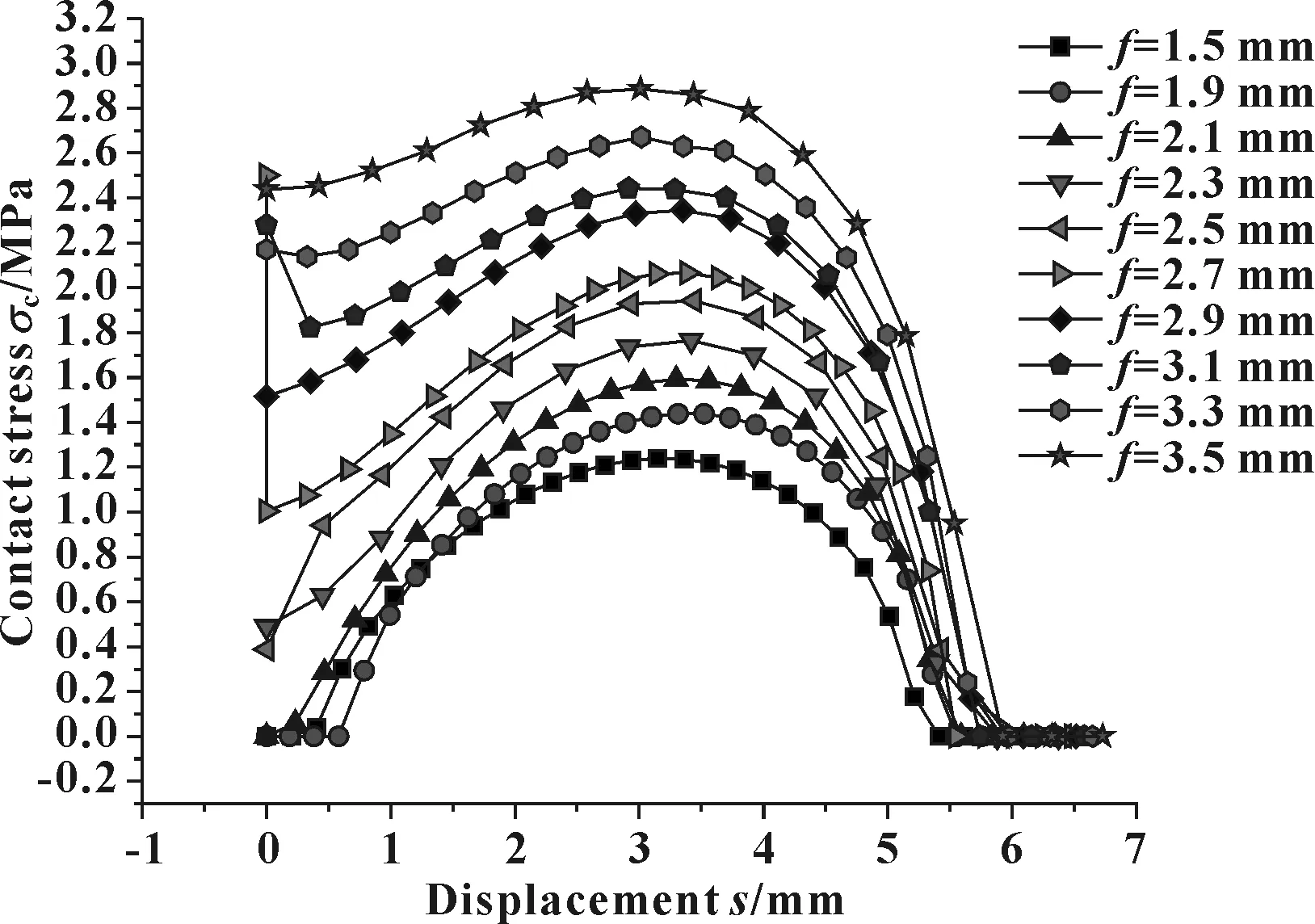
图28 不同f值时预紧压缩接触应力分布

削斜高度f取不同值，间隙达到2 mm时，接触应力的分布如图29所示。可见f值的增大，2 mm间隙时的密封性也增强。

图29 不同f值及2 mm间隙时接触应力分布

削斜高度f取不同值，间隙达到4.5 mm时，接触应力分布如图30所示，密封圈的变形如图31所示。可见，f值增大，4.5 mm间隙时密封带长度也增大，密封性能增强。

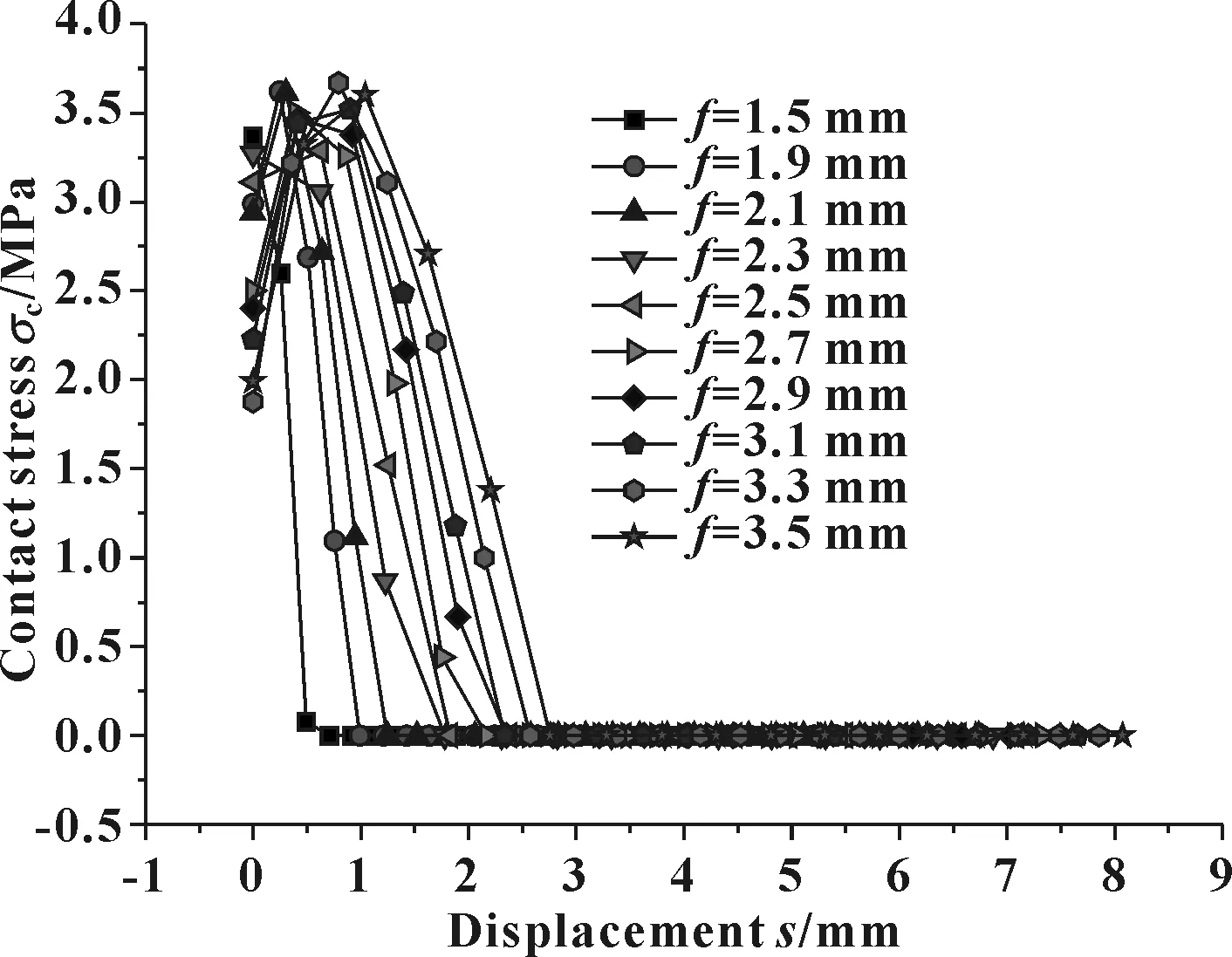
图30 不同f值及4.5 mm间隙时接触应力分布

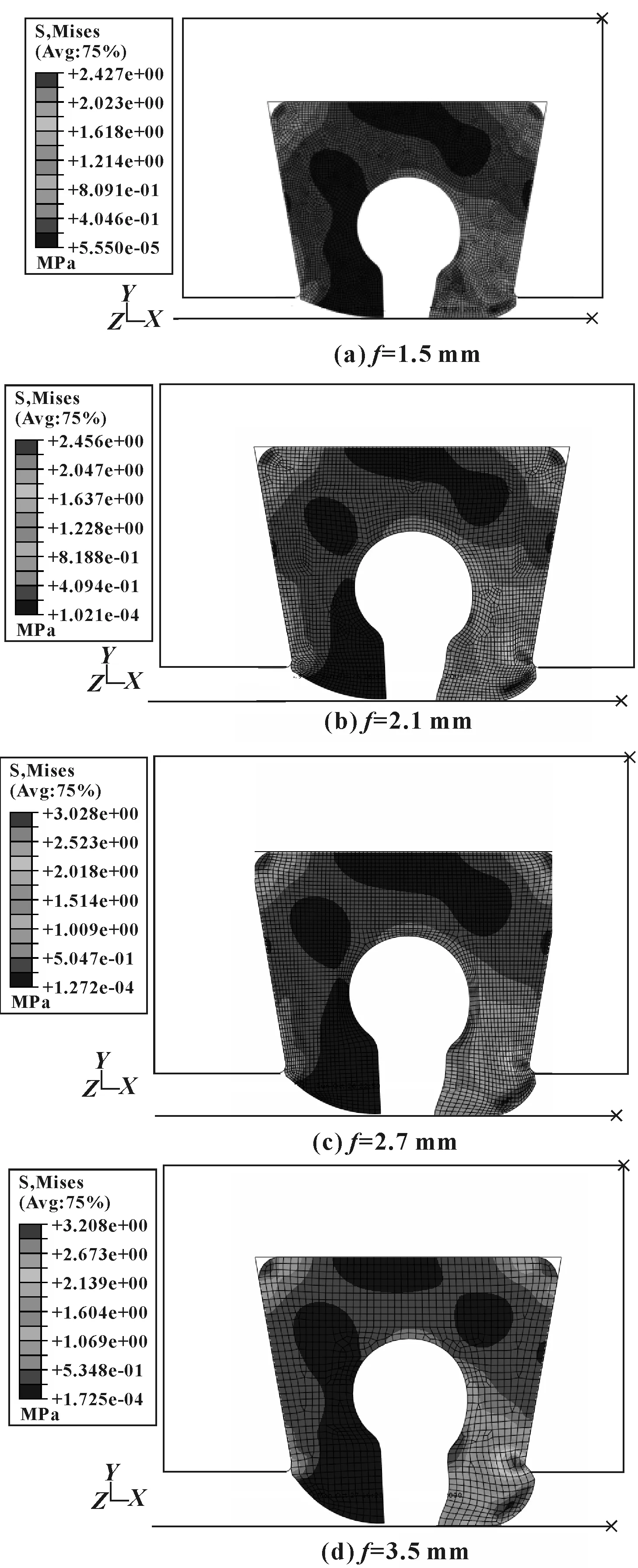
图31 不同f值及4.5 mm间隙时变形

将以上计算结果列于表1，可见对大间隙密封性能影响较大的几何参数为r、d、f。

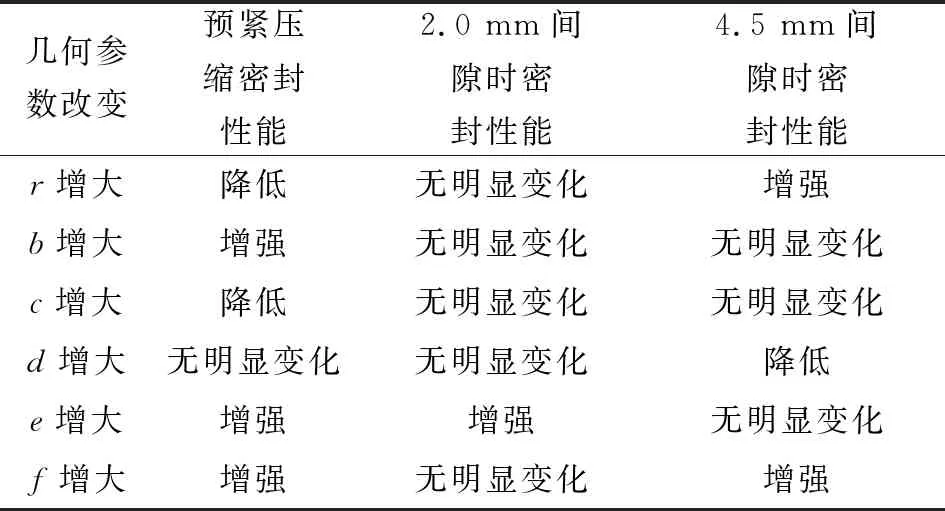
表1 几何参数对密封性能影响

3.2 密封圈截面几何参数优化

根据3.1节计算分析结果，对密封圈截面几何参数进行优化设计，优化后方案与原方案密封圈截面几何参数见表2。对优化后的密封圈进行大间隙工况的仿真计算，计算的结果见图32—34。

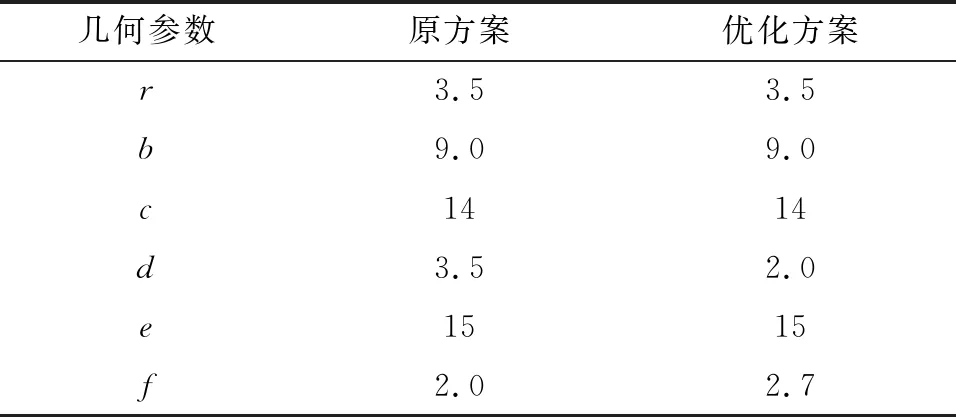
表2 优化方案与原始方案几何参数对比

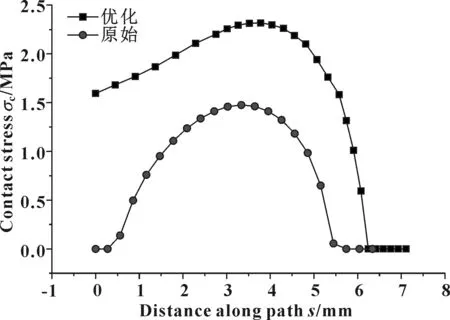
图32 优化方案与原方案预紧压缩接触应力对比

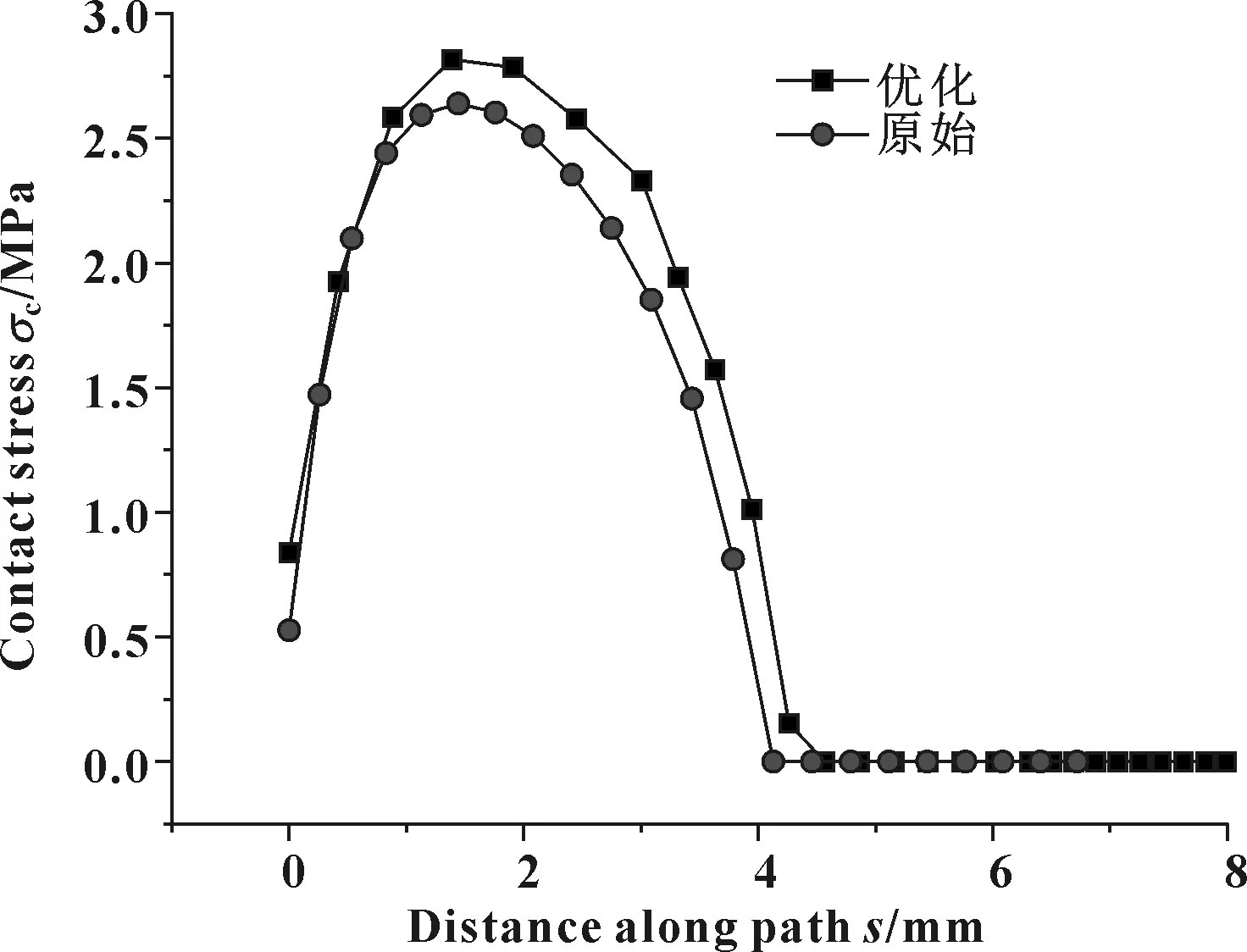
图33 优化方案与原方案2 mm间隙时接触应力对比

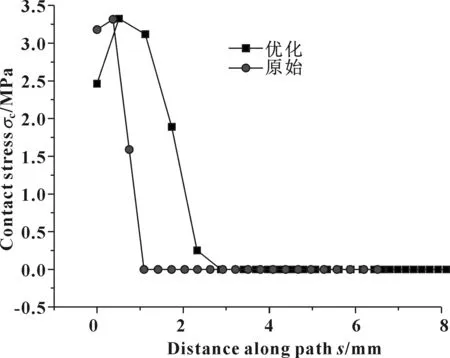
图34 优化方案与原方案4.5 mm间隙时接触应力对比

由图32—34可见，优化后的密封圈在预紧压缩情况下，其接触应力最大峰值和密封带的长度均明显大于原始密封圈结构；2 mm间隙时的接触应力分布两者相近；4.5 mm间隙时，优化后的密封圈接触应力峰值与原始密封圈接近，而密封带长度明显增大。

综上所述，优化后的密封结构综合密封性能优于原密封结构。针对优化后的密封结构进行了密封性能试验验证，其密封性能能够满足指标要求。

4 结论

(1)典型算例中C形密封圈结构在流体载荷增加的情况下(<2.0 MPa)，接触应力的峰值也随之增加，并始终大于流体载荷，密封圈结构具有自密封特性。

(2)大间隙密封工况下，C形密封圈截面开口半径r、开口间隙d和削斜高度f对其密封能力影响显著。

(3)仿真计算结果表明，优化后的密封结构在预紧压缩和大间隙工况下的密封性能均优于原始密封结构。