SPSS在正交设计中的应用
2020-10-09陈敏

摘 要:正交试验设计,是指研究多因素多水平的一种试验设计方法,而SPSS软件最突出的特点就是操作界面极为友好,输出结果美观漂亮,具有完善的数据输入、编辑、统计分析、报表、图形制作等多项功能。本文运用SPSS软件对试验设计中的正交设计的部分案例进行分析,并比较输出结果与理论结果的不同之处。
关键词:正交设计;SPSS;贡献率分析;方差分析
试验设计是使用频率最高的统计方法之一。著名统计学家G.E.P.Box说过,假如有10%的工程师使用各种试验设计方法,产品的质量和数量都会得到很大提高。质量工程学创始人田口玄一(G.Taguchi)博士说过,不懂试验设计的工程师只能算半个工程师。可见普及试验设计方法对我国现代化建设是一件重要的战略措施。试验设计至今已有近80年的历史,是英国统计学家R.A.Fisher创立的,产生了许多试验设计的方法,其中有些方法已经被近30年创立的新方法所替代,但是正交设计却是较实用较有特色的一种方法,也是试验优化的常用技术。什么是试验优化?试验优化是指在最优化思想的指导下,进行最优设计的一种优化方法。它是根据试验不同的优良性,合理设计试验方案,科学处理试验数据,有效控制试验干扰,全面进行优化分析,从而达到直接实现优化目标的目的。而SPSS是一种统计学的常用软件之一,具有强大的功能,所以我们在统计教学中,也经常运用SPSS软件来进行许多统计专业课程的教学,试验设计这门课程也不例外。本文的案例是介绍为解决铬污水超标问题,需要进行改进工艺,以提高树脂的使用时间,为此进行试验,根据以往经验,考察四个三水平因子A(pH值)、B(污水进水流量(m3/h))、C(污水进水浓度(mg/l)))。
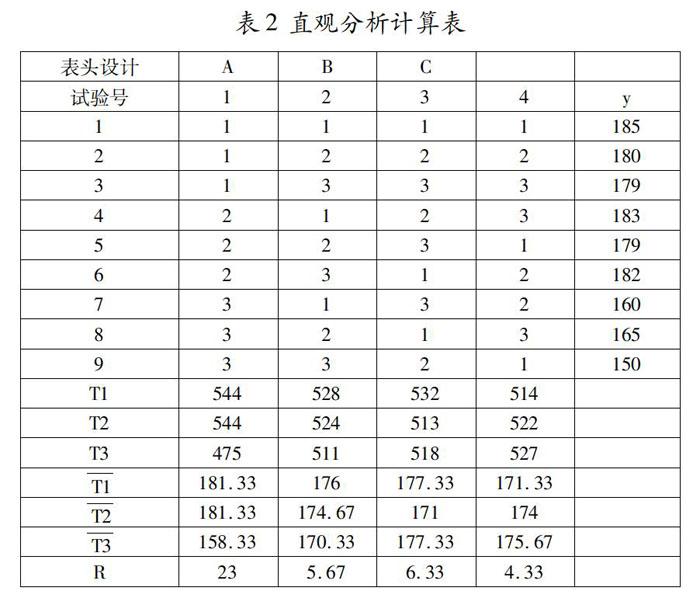
我们选用L9(34)安排试验,将4个因子依次放在三列上,通过观测得到9次试验的使用时间数据如下:
185 180 179 183 179 182 160 165 150
1 直观分析法
在表2中的T1、T2、T3表示各因素各水平下的总和,R表示同一因素各水平下平均使用时间的极差(极差=平均使用时间的最大值-平均使用时间的最小值),极差一般反映各因素的水平变动对试验结果影响的大小,极差大就说明该因素的水平变动对实验结果的影大。由表2得到:RA>RC>RB,说明因子A的影响最大,从而得出,利用直观分析法得出的最优水平组合是:A1B1C1或者是A2B1C1,即最优工艺是pH值为4.0或者4.5,污水进水流量为3m3/h,污水进水浓度为30mg/l。按此条件的试验在这9次实验中并没有出现,通过补充试验,得到树脂的使用时间为190,大于正交试验中的最高值185,说明利用正交试验改进工艺是正确的方法。
2 方差分析法
数据的直观分析方法虽然简单,计算量小,但它的不足之处是不能回答哪些因子对试验指标有影响,哪些结果对试验指标没有影响,最重要的是不能估计试验误差。因此,我们只能对实验结果做方差分析。而方差分析需要对实验结果作出若干假定:(1)假定在同一水平下试验结果的全体构成一个总体,服从正态分布;(2)各正态总体的方差是相同的;(3)各正态均值与水平组合有关;(4)不同水平组合下的试验是相互独立进行的。在上述假定下,方差分析的任务就是对如下三对假设分别作出检验:
HA0:a1=a2=a3=0,HA1:a1,a2,a3不全为零
HB0:b1=b2=b3=0,HB1:b1,b2,b3不全为零
HC0:c1=c2=c3=0,HB1:c1,c2,c3不全为零
对于方差分析来说,我们先要进行平方和的分解,考察引起y1,y2,…,yn波动的原因,将其用平方和的式子表示出来。
ST=∑ni=1(yi-y-)2 fT=n-1
Sj=nq∑qk=1(Tjk-y-)2 fj=q-1,j=1,2,…,p
ST=∑pj=1Sj j=1,2,…,p
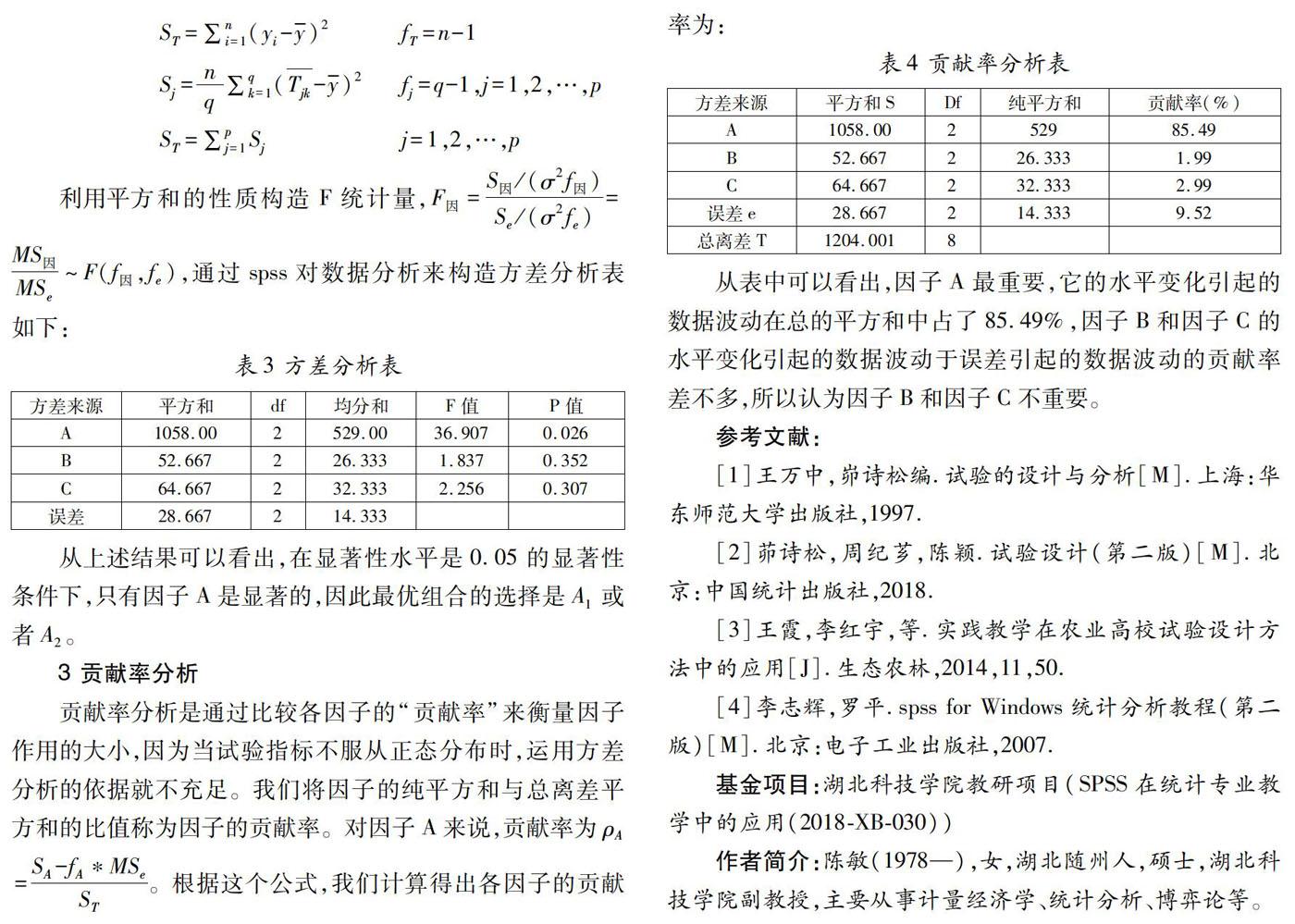
利用平方和的性质构造F统计量,F因=S因/(σ2f因)Se/(σ2fe)=MS因MSe~F(f因,fe),通过spss对数据分析来构造方差分析表如下:
从上述结果可以看出,在显著性水平是0.05的显著性条件下,只有因子A是显著的,因此最优组合的选择是A1或者A2。
3 贡献率分析
贡献率分析是通过比较各因子的“贡献率”来衡量因子作用的大小,因为当试验指标不服从正态分布时,运用方差分析的依据就不充足。我们将因子的纯平方和与总离差平方和的比值称为因子的贡献率。对因子A来说,贡献率为ρA=SA-fA*MSeST。根据这个公式,我们计算得出各因子的贡献率为:
从表中可以看出,因子A最重要,它的水平变化引起的数据波动在总的平方和中占了85.49%,因子B和因子C的水平变化引起的数据波动于误差引起的数据波动的贡献率差不多,所以认为因子B和因子C不重要。
参考文献:
[1]王万中,峁诗松编.试验的设计与分析[M].上海:华东师范大学出版社,1997.
[2]茆詩松,周纪芗,陈颖.试验设计(第二版)[M].北京:中国统计出版社,2018.
[3]王霞,李红宇,等.实践教学在农业高校试验设计方法中的应用[J].生态农林,2014,11,50.
[4]李志辉,罗平.spss for Windows统计分析教程(第二版)[M].北京:电子工业出版社,2007.
基金项目:湖北科技学院教研项目(SPSS在统计专业教学中的应用(2018-XB-030))
作者简介:陈敏(1978—),女,湖北随州人,硕士,湖北科技学院副教授,主要从事计量经济学、统计分析、博弈论等。
