紧急事件下应急模型的建立与研究

邵琦

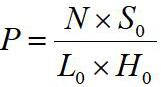
【摘  要】本文主要针对卢浮宫的疏散讨论的研究，利用卢浮宫内外任何一处发生危险事件，做了模拟卢浮宫方面的参考继而引导人们进行疏散。首先对于每个疏散通道正在使用时其容纳疏散人员的数量是动态变化的，而模型中给出了卢浮宫方面应该让这些疏散通道处于一种什么样的容纳疏散人员情况，其次使得卢浮宫方面得以此为参考进行一个安全并且快速的疏散。能根据危险事件发生的地点来进行对群众的引导疏散，让卢浮宫方面清楚地看到哪些疏散口是值得去引导群众疏散的。最后能大致判断哪些疏散口有相对较大几率发生瓶颈，进而调动更多的工作人员进行有效安全的疏散。能大致掌握每一层楼的疏散时间以便卢浮宫方面对一个疏散整体有一个把握，可以作为安排工作人员在每一层楼的人员数的依据，达到工作人员的有效调动。

【关键词】疏散;动态变化;引导群众疏散

引言

因近期法国的恐怖袭击越来越多，需设计巴黎卢浮宫疏散计划，指引人们找到一个最佳出口，在疏散的同时，也要实现相应应急管理工作。2017年接待游客量超过810万，此处到馆人数说明超于游客数量，还带来了一个关于访客信息的更高难度挑战：包括多团体，多语 ，残疾游客等游客的丰富度。 每一层对应标有上下扶梯或楼梯（疏散不考虑电梯），位于这5层的380，000件展品占地约72，735m2，此处展品的占地面积可理解为人群所在地面积，因为大部分人进博物馆都是为参观不同展品而去。卢浮宫共有4个主要入口（均位于0层），分别是大众化的金字塔主入口（下至-1层，2层均可去往3个展馆），另外3个通常保留给团队和博物馆会员的入口，分别是狮门入口，卡鲁塞勒商廊入口，黎塞留通道入口。同时，卢浮宫也有大大小小的不同出口点如（服务门，员工入口，VIP入口，紧急出口，君主建立的老秘密入口）数量若干。

1.模型的建立

设立事件A1 =“人群正常选择金字塔入口作为卢浮宫的出入口”，A2 =“人群正常选择狮门作为卢浮宫的出入口 ”A3  =“人群正常选择卡鲁塞勒商廊作为卢浮宫的出入口 ”，A4 =“人群正常选择黎赛留通道作为卢浮宫的出入口 ”，T =“恐怖事件发生 ”，其中，基于客观事实考虑，人群每天一般只从4个主出入口出入卢浮宫，其中金字塔入口是普通大众出入，另外3个则供团体或会员出入。每一起恐怖袭击事件要么发生，要么不发生，所以可看作服从各自二项分布的各自独立的随机变量。由于恐怖事件一旦发生，即需立刻疏散人群。又因为人群疏散过程中到达的终点，会是4个主出入口其中的一个。作为描述发生恐怖袭击事件发生时，人们会选择哪个主出入口作为疏散终点。为便于确定表达式中各概率值，我们假定存在一个事发点，并假定事发点与出入口均事发点分别与金字塔入口，狮门入口，卡鲁塞勒商廊入口，黎塞留通道入口连线所成线段距离S1，S2，S3，S4，当然，基于现实中事发点的不可控因素，我们引入作为恐怖袭击事发中心与我们预测的事发中心地点的一个距离误差。所以，根据疏散时人群的心理因素可推出一个就近选择原则，即人群疏散时会就说明适用于个门各自概率的计算，即事发地点与分别与个门连线的空间线段距离都差不多，每一个门都可作为人群选择疏散的疏散终点。不存在不符合3种门的情况，因为狮门与金字塔入口是相互靠近，黎塞留通道和卡鲁塞勒商廊是相互靠近，形成了两两配对选择的情况。

2.模型的求解

鉴于卢浮宫规模之庞大，疏散的人员数量之巨大，在这里所研究的对象将不再是通常的单位个人，而转化为单位股人流，人流由一群人构成，其理想状态是人流里人与人间隔相同、步调一致。人流密度反映了人流内的人员稠密程度，考虑到计算上的相融性，将人抽象成其垂直投影在地上的面积，即人流密度为：

其中N为人流内人数，S0为u人均垂直投影面积，L0为人流的长度，H0为人流的宽度。由于人流内有着不同年龄段的人员，出平均年龄为37岁，以此来进行计算投影面积S0，即S0为青年人的平均占地面积。通量反映为单位时间内通过一定宽度上一个断面的疏散人员的占地面积，即通量为：W =ρvH

其中v为人流平均速度，H为宽度。面通量反映为单位时间内通过单位宽度上一个断面的疏散人员的占地面积，根据Predtechenski和Milinskii的研究，人流在正常情況下的平均速度为：

v0=112p4-380p+434p2-217p+57

其中p≦0.92，在p超过这一数值时人流的疏散会发生拥挤现象。

在疏散时人流的平均速度会相对较快，因此疏散时人流在水平通道内的行走速度为：

v1 = k1v0

其中，k1 =1.49-0.36p，因此疏散时人流在穿越楼梯时速度可近似看作v1。

楼道内人员的疏散：通常情况下，楼道内人员也成一股人流，人流宽度随楼道宽度而定，而考虑到人们之间留有空隙以及一些不可利用的空间比如与墙壁距离微小的距离内可能摆放有障碍物，因而导致楼道内宽度有一个有效宽度。由于p=0.92时为人流是否拥挤的临界点，理想状态下假设人流有着倾向于最优的通行速度进行疏散，即楼道口附近的p值达到pmax=0.92，而相应的面通量Q也达到Qmax，即在 max值下的面通量。楼层进行疏散时，以下的讨论皆视为每层楼的楼梯口同时开始疏散并且同时完成疏散，并且忽视疏散开始时第一股人流到达楼道口的时间。n1×S0为该层楼人数总的占地面积，则n1×S0有减小的趋势：

△n1×S0=（Q11+Q12-Q13-Q14）×t1×H

t1为该层楼及上层楼共同完成疏散所需的时间。而若P在这一过程中大于0.92，则会发生拥挤现象导致人流排队通过楼道口。由于四个出口给出了理想状态下人流分布情况，则依此来决定各个楼道口的人流分布情况，可粗略地认为理想情况下选择各个楼道口的概率与其距离危险源的空间距离成线性关系，因此来进行线性回归。

3.结语

每一层工作人员可依据此时间进行流动而防止不必要的人力资源浪费。在有序过程中计算得出的每个楼道口的面通量值可以作为卢浮宫工作人员关注点，其中面通量若接近最大值则说明此处易发生人员拥挤导致的瓶颈发生，应该重点注意这些地方并且安排工作人员前往维持有序地进行疏散，若楼道口实际面通量有出入，则应该安排工作人员进行引导群众进行疏散达到最安全的疏散效果。将有序状态下疏散的每一层楼及总时间与无序状态下疏散的每一个相应时间进行对比，其对应时间的差值大小可作为卢浮宫方面进行参考，差值越大则表明此处所调用的工作人员越多来进行有向疏散引导。

参考文献

[1]PredtechenskiV.M.，Milinskii.PlanningofFootTraffcFlowinBuildings[M].India：Am