集权-分权博弈视角下企业结构的战略选择
2020-10-09刘冰倩殷明娥
王 静, 刘冰倩, 殷明娥
(辽宁师范大学 数学学院,辽宁 大连 116029)
理论研究表明,企业的战略组织结构与其分部门的业绩评价之间不可避免的相互作用和影响.尽管如此,早期的基于转移定价的企业组织设计问题主要聚焦在最终产品市场存在竞争时的战略决策,而没有考虑存在中间产品外部供应商的情形[1-2].然而,企业生产最终产品所需的中间产品同时需要外部和内部供应的现象普遍存在.比如,计算机供应商开发新产品时既需要他们自己拥有的硬件组成部分,又需要由外部供应商提供的软件部分.依赖外部供应商供货的转移定价模型最早由Arya和Mittendorf[3]提出,他们考虑了两种模型框架:一种是一家企业可以选择集权和分权组织结构,而其竞争对手的组织结构外生固定;第二种是两家企业同时在集权和分权结构之间进行战略选择,而外部供应商对两家企业进行差异定价.Liu等[4]对上述模型做了进一步推广.
在上述文献中,都假设所有厂商皆采取相同的竞争策略.然而,企业间所采取的竞争策略未必一定相同.例如,Sato[5]指出, 日本家电厂商中Matsushina倾向于采用产量策略,而Sanyo厂商偏好价格策略.这种混合竞争模式最早由Singh和Vives[6]提出.经验研究表明,关于混合竞争模型的研究有助于进一步深化对寡头垄断市场的理解[7].王静和殷明娥[8]考虑了下游市场存在混合寡头竞争,上游市场存在外部供应商时的企业战略组织决策问题.在文献[8]的模型框架下,本文基于集权-分权博弈的视角,研究企业的战略组织选择问题.
1 模型构建
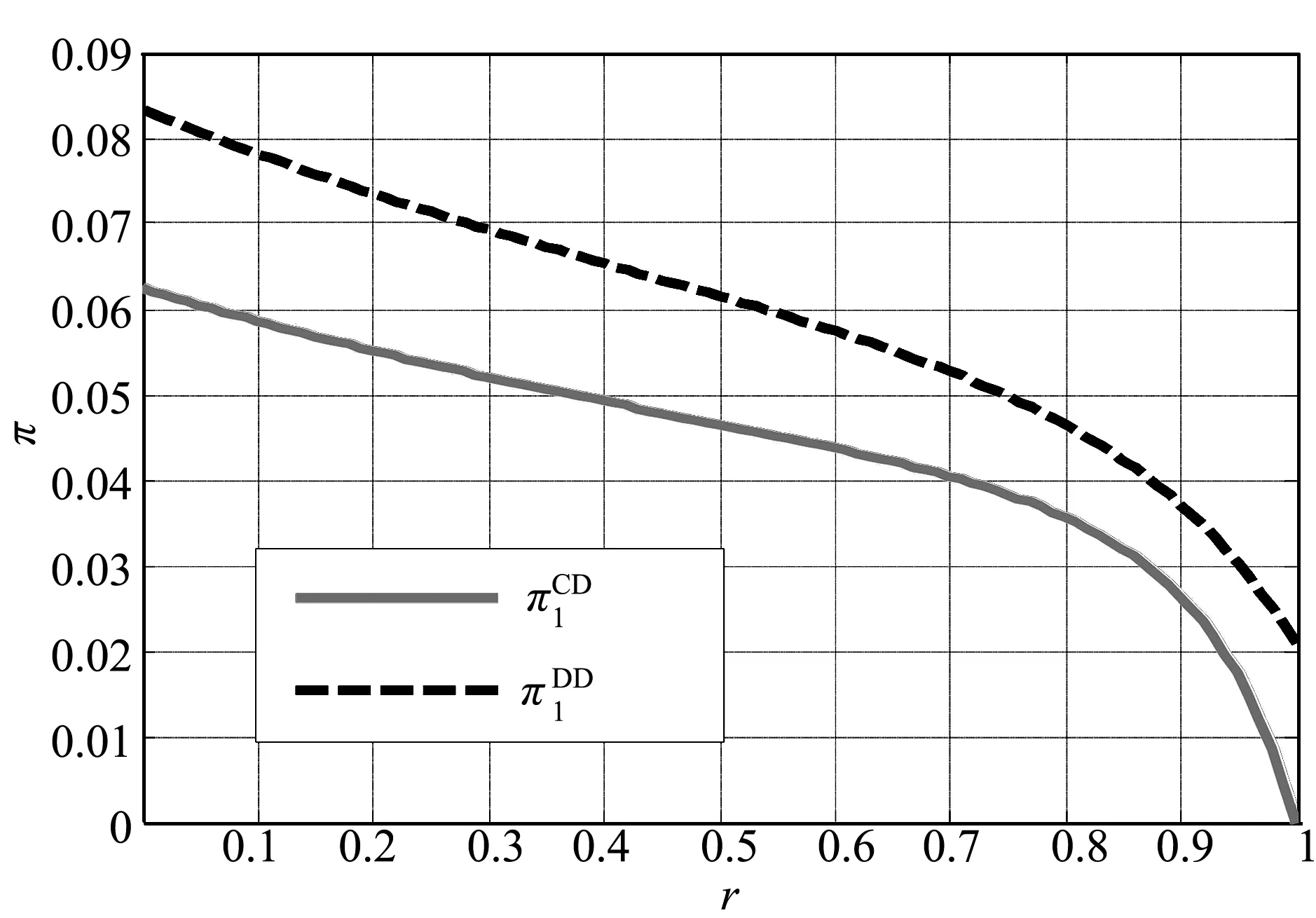
企业F1生产的最终产品需要两种中间产品,一种由企业内部生产,单位边际成本为cI;外部采购产品的单位边际成本为cE,并记c=cI+cE. 假设企业所需的外部中间产品从唯一的供货商购买.F1在最终产品市场上存在一个竞争对手F2.为简化分析过程,假设其边际成本为c且条件c pi=b-qi-rqj,i,j=1,2,i≠j. (1) 其中,pi和qi分别表示F1(i=1)和竞争对手F2(i=2)在最终产品市场的价格和产量,参数r∈(0,1)为最终产品的差异系数.当r→0时表示两种产品是相互独立的;当r→1时,两种产品则是同质的. 外部供应商为两家企业提供中间产品的价格分别为ω1和ω2;当企业采用分权组织形式时,中间产品的内部转移价格分别为t1和t2. 假设F1和F2采取不同的竞争策略:F1采取数量策略而F2采取价格策略.企业需要在集权和分权两种组织形式做出选择.当两者都采用集权(分权)形式时,相关变量加注上角标CC(DD);当F1集权(分权)而F2分权(集权)时,相关变量加注上角标CD(DC). 采用动态博弈的逆向归纳方法求解.企业F1和竞争对手F2的问题分别为 (2) (3) 根据式(2),求解最大化问题的一阶条件得 (4) 类似地,由式(3)得 (5) 联立式(4)和式(5)以及式(1)得 (6) (7) 其中,ηi=ωi-cE,i=1,2. 在集权情况下,外部供应商的问题为 (8) 将式(6)和式(7)代入式(8),由最大化问题的一阶条件得 (2-r)(b-c)-4η1+2rη2=0, (9) (2-r-r2)(b-c)+2rη1-2(2-r2)η2=0. (10) 联立式(9)和式(10)得 (11) 将式(11)分别代入式(6)和式(7)得均衡产量分别为 类似于第2节的求解方法,此时企业F1的下游问题为 (12) 竞争对手F2的问题为式(3). 根据式(12),求解最大化问题的一阶条件得 (13) 联立式(5)和式(13)以及式(1)得 (14) (15) 其中,ξi=ti-cI,i=1,2. 在此情况下,外部供应商的问题为式(8),F1的上游部门的问题为 (16) 将式(14)和式(15)代入式(8)和式(16), 由最大化问题的一阶条件得 (17) 求解线性方程组(17)得 (18) 将式(18)中各式代入式(14)和式(15)得 在这种情况下,企业F1的问题仍为式(2),竞争对手F2的下游问题为 (19) 求解最大化问题的一阶条件得 (20) 联立式(4)和式(20)以及式(1)得 (21) (22) 外部供应商的问题为式(8),F2的上游部门的问题为 (23) 将式(21)和式(22)代入式(8)和式(23), 由最大化问题的一阶条件得 (24) 求解线性方程组(24)得 (25) 将式(25)中各式代入式(21)和式(22)得 企业F1和竞争对手F2的下游部门的问题分别为式(12)和式(19),由最大化问题的一阶条件得 (26) (27) 外部供应商的问题为式(8),F1和竞争对手F2的上游部门的问题分别为式(16)和式(23),将式(26)和式(27)分别代入式(8),式(16)和式(23), 由最大化问题的一阶条件得 (28) 解线性方程组(28)得 将以上各式代入式(26)和式(27)得 将上述利润函数的图像描绘在图1~图4中. 图1和图2显示,无论F2采取什么组织形式,F1采取分权为最优策略;同样,图3和图4显示,无论F1采取什么组织形式,F2采取分权为最优策略.因此,两家企业博弈的唯一纳什均衡解为双方均选择分权结构. 图1 F2集权F1两种组织形式的利润比较 图2 F2分权F1两种组织形式的利润比较 图3 F1集权F2两种组织形式的利润比较 图4 F1分权F2两种组织形式的利润比较 企业的战略组织设计是管理界一直关注的热点问题,研究的角度包括经济学、金融学、产业组织行为学等方面.在研究过程中,任何组织设计都需要运用会计手段对其进行评估. 衡量企业相关部门获利能力就是一种重要的会计度量手段,这种度量一般取决于企业内部的转移定价决策.转移定价的主要功能之一是协调企业内部各分企业或利益关联方之间的关系,实现其整体战略目标,谋求企业整体利益最大化.基于分权-集权博弈的视角,本文在混合竞争条件下,当中间产品存在垄断外部供应商时,研究两个竞争企业的战略组织问题.结果表明,双方均选择分权结构为唯一的纳什均衡解.采用本文的研究方法,还可以得到当中间产品存在两个独立的外部供应商时的相关博弈结果.2 F1和F2都为集权
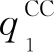
3 F1分权F2集权
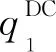
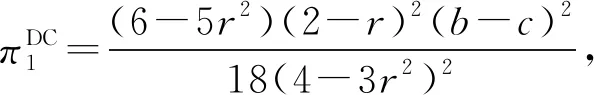
4 F1集权F2分权

5 F1和F2都为分权
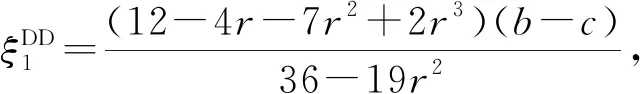
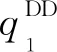



6 结 论
