多激励条件下高速列车牵引变压器悬挂参数选择研究

贺小龙， 罗天洪， 伍国果， 唐帮备， 刘潮涛

(1. 重庆文理学院 智能制造工程学院， 重庆 402160； 2. 西南交通大学 牵引动力国家重点实验室， 四川 成都 610031)

高速列车牵引变压器(见图1、图2)将接触网上取得的25 kV高压电变换为供给牵引变流器及其他电器工作所适合的电压，是高速列车关键附属设备之一[1]。牵引变压器通常拥有较大的自身质量,且携带复杂激励源，其振动行为对整个车辆系统的振动特性起着重要影响。首先，变压器振动过大会直接削弱车辆的乘坐舒适性；其次，变压器振动过于剧烈还会恶化车下设备长期稳定的工作环境；最后，变压器振动过大会对车下设备悬吊机构疲劳可靠性造成影响。因此，在变压器设计初期，就需要考虑车辆设备的耦合振动问题。众所周知，牵引变压器的悬挂参数是直接影响变压器振动性能的重要因素，它甚至会影响到整个车辆耦合系统的动力学性能。对牵引变压器悬挂参数进行合理设计具有重要意义。

图1 某型高速列车牵引变压器实物

图2 车辆设备系统示意

关于车下设备悬挂参数设计，大量学者对其进行了研究。黄晓宇[2]分析了高速列车牵引变压器隔振器刚度对车辆振动特性的影响；为了有效衰减车体的垂向弯曲模态振动，宫岛等[3-4]考虑基于动力吸振理论对车下设备悬挂参数进行设计，并探讨了车下设备悬挂静扰度与车辆运行平稳性的映射关系；孙文静等[5]研究了车下设备悬挂参数与车辆垂向弯曲模态频率的对应关系；石怀龙等[6]将车体考虑成弹性欧拉梁，分析不同种类设备悬挂频率、联接阻尼、质量和安装位置对车体振动的影响规律，同时将设备考虑成动力吸振器来确定最优悬挂频率，以达到衰减车辆弹性振动的目的；通过建立车辆设备刚柔耦合Simpack模型，吴会超等[7]探究了车下设备分别采用刚性吊挂和弹性吊挂时车辆的振动特性，并明确了设备悬挂参数与车体模态的匹配关系；文献[8-9]中提出计算整备状态下高速列车车体一阶垂向弯曲模态频率的数值及解析方法，并基于解析方法及隔振理论提出了车下设备与车辆模态匹配原则，设计了车下设备悬挂参数并针对设计结果进行试验验证。

综合国内外学者研究现状可知：国内外学者虽然对变压器等车下设备悬挂参数与车辆设备耦合系统振动关系进行了研究，但是都未考虑轮轨激励和设备激励共同作用下变压器悬挂参数与车辆振动特性的影响关系，并且对变压器悬挂参数设计也未考虑车辆实际运行时所受到的多激励条件。对此，本文在之前研究成果的基础上，考虑车辆系统在同时受轮轨激励和设备激励条件下变压器悬挂参数对车辆系统振动特性的影响规律，并在多激励条件下对变压器最优悬挂参数进行设计。研究成果可以为高速列车牵引变压器悬挂参数的设计提供指导。

1 车辆设备系统建模

车辆-变压器耦合系统模型见图3。图中车辆设备系统包含1个车体、2个转向架、4个轮对以及1个牵引变压器。除车体为弹性体外，其余为刚体，并且假设轮轨完全接触；mc为车体质量；L为车体长度；v为车辆运行速度；Jc为车体转动惯量；me为设备质量；Je为设备点头转动惯量；mb为转向架质量；Jb为转向架点头转动惯量；l1、l2分别为车辆二系悬挂距端部距离；le1、le2为变压器悬挂位置；ac表示车辆定距之半；hc为二系悬挂与车体重心的垂向距离；hb2为二系悬挂与转向架重心的垂向距离；hb1为一系纵向悬挂与转向架重心的垂向距离；ab表示转向架定距之半；ae1、ae2分别为设备悬挂距其质心纵向距离[10]；kbz、kcz分别表示一、二系悬挂垂向刚度；cbz、ccz分别表示一、二系悬挂垂向阻尼；kbx、kcx分别为一、二系悬挂纵向刚度；cbx、ccx分别为一、二系悬挂纵向阻尼；kcθ、ccθ为二系悬挂点头刚度、阻尼；ke、ce为设备悬挂刚度、阻尼；kh为轮轨接触垂向刚度；krz、crz为钢轨支撑刚度、阻尼；mw为轮对质量；mr为接触钢轨质量；w(x,t)为车体垂向振动位移，其中x为车体沿纵向位置坐标，t为时间；zc表示车体沉浮位移；θc为车体点头位移；zb1、zb2为两端转向架沉浮位移；θb1、θb2为两端转向架点头位移；xb1、xb2为前、后端转向架纵向位移；ze、θe分别为设备的沉浮、点头位移；zw1～zw4、xw1～xw4分别为轮对1～4的垂向位移、纵向位移；zr1～zr4为接触钢轨1～4的垂向位移[11-13]。

图3 车辆设备耦合系统模型

车体的垂向振动位移为三阶模态的叠加

w(x,t)=zc+(x-2/L)θc+X1T1

( 1 )

式中：T1为车体垂向弯曲模态坐标；X1为车体垂向弯曲阵型函数。车体的运动方程描述为[14-15]

( 2 )

式中：E为车体的弹性模量；I为车体的截面惯性矩；ξ为车体结构阻尼系数；ρ为车体单位长度质量；δ(x)为狄拉克函数；Fzc1、Fzc2为二系悬挂垂向作用力；Mc1、Mc2为二系悬挂作用在车体上的力矩；Fxc1、Fxc2为二系悬挂纵向作用力；Fze1、Fze2为设备悬挂垂向作用力。

前后端构架沉浮运动方程分别为

( 3 )

( 4 )

前后端构架点头运动方程分别为

( 5 )

( 6 )

式中：Fzbk、Fxbk分别为一系悬挂垂向、纵向作用力。

转向架纵移运动方程为

( 7 )

( 8 )

牵引变压器沉浮运动方程为

(2kei[w(lei,t)-(ze±aeiθe)]}

( 9 )

牵引变压器点头运动方程为

(2kei[w(lei,t)-(ze±aeiθe)]}

(10)

轮对的纵向位移方程为

(11)

轮对的沉浮运动方程为

(12)

式中：Qk为轮对的垂向作用力；kh为轮轨接触刚度。

接触钢轨的垂向运动方程为

(13)

式中：Fzrk为路基对钢轨的支撑作用力。

2 车辆系统多激励条件分析

车辆在运行过程中会受到轮轨激励作用，并且激励特性会随着车辆速度、运行线路工况及车辆工作状态的变化而变化，文中将采用京津城际轨道谱作为车辆系统的轨道激励[16]。

图4 变压器结构示意

除了受轮轨激励作用，车辆系统还受到牵引变压器自身激励的影响。牵引变压器主要由变压器本体和冷却风机组成，见图4。变压器激励主要分3种：绕组在电动力作用下产生的激励；由磁致伸缩效应引起的铁心激励；冷却风机转子动不平衡引起的激励。

其中绕组振动激励力为[17]

4ω2F2sin(2ωt+φ)

(14)

式中：F1为绕组自激励幅值；F2为绕组受迫振动激励幅值；ω0为绕组固有频率；ω为受迫振动频率；θ、φ分别为初始相位。

磁致伸缩现象的磁场力为[18]

(15)

(16)

冷却风机激励力为

F(t)=m0e0γ02sinγ0t

(17)

式中：F(t)为激扰力；m0为旋转部分的不平衡质量；e0为偏心距；γ0为角速度，且有γ0=0.105n0，其中n0为转速。旋转机械设备通常采用当量偏心距来计算激扰力。文中计算风机激励力e0取0.25。

结合上述牵引变压器激励计算方法，可计算出变压器的本体激励为

Fb=F1sin2πf1t+F2sin2πf2t+F3sin2πf3t

(18)

式中：f1、f2、f3分别为基频激励(50 Hz)、2次谐波激励(100 Hz)、3次谐波激励(200 Hz)；F1、F2、F3分别为基频及2、3次谐波激励幅值，经计算F1、F2、F3分别为351.5、141、23 N。

风机的激励为

Ff=F4sinω1t+F5sinω2t

(19)

式中：ω1、ω2分别为风机2种转速下激励频率；F4、F5分别为风机在两种转速下激励幅值，其值分别为46.25、15.5 N，风机1和风机2激励力相同。

3 车辆系统振动指标计算

本文基于翟婉明院士[19]提出的新型快速显示数值积分方法求解车辆系统振动响应。图5为车辆运行速度为200 km/h条件下车辆中部及变压器的垂向加速度振动响应。

图5 车辆及设备垂向振动响应

本文采用UIC 513—1994标准[20]中的方法计算车辆舒适度指标

(20)

式中：C1为舒适度指标；ax、ay、az分别为纵向、横向、垂向经过加权滤波后的加速度有效值。

振动烈度定义为频率10～1 000 Hz范围内振动速度的均方根值，它能简明、综合、实用有效地反映一台设备振动状态的特征量。若已知振动速度信号为v(t)，计算时所取时间为T，振动烈度可按如下公式计算[21]

(21)

式中：V1为信号在时间段(0，T)上平均功率的均方根或有效值。根据文献[22]中的规定，牵引变压器要想达到能长期安全运行的振动水平，其振动烈度不宜超过4.5 mm/s。

4 设备悬挂参数对车辆系统振动影响分析

通过计算，可以得到车辆舒适度指标和变压器振动烈度随速度变化趋势，见图6、图7。由图可知：随着速度增加车辆舒适度指标和变压器振动烈度逐渐增大，车辆一、二位端舒适度指标变化趋势基本一致，车辆端部舒适度指标明显高于中部，变压器振动烈度随着速度增加逐渐增大，速度超过160 km/h时振动烈度会超过4.5 mm/s。

图6 舒适度指标计算结果

图7 变压器振动烈度计算结果

变压器自身质量较大，其悬挂位置会对车辆舒适性和自身振动烈度产生影响，因此需要研究设备悬挂位置对车辆系统振动特性的影响规律。考虑车下设备舱实际空间结构特点，确定变压器悬挂质心位置距车辆端部纵向距离变化范围为5.4～16 m，其中数值越小表示变压器悬挂越靠近车辆一位端，数值越大表示变压器悬挂越靠近车辆二位端。其中车辆速度变化范围为10～400 km/h，步长取10 km/h。车辆一位端、中部、二位端舒适度指标计算结果见图8、图9。由图8可知：车辆中部、端部舒适度指标随速度增加而增加，当车速高于150 km/h，变压器悬挂位置对车辆舒适度指标的影响开始凸显；变压器悬挂越靠近端部，车辆端部舒适度指标越小，越靠近中部，车辆中部舒适度指标越小，这种影响在180～200、230～330 km/h时最为明显。

图8 变压器悬挂位置对车辆舒适度指标影响

图9 变压器振动烈度

图9为变压器振动烈度变化趋势。由图可知：变压器振动烈度随车辆速度的增加逐渐增大，但是在某些速度下变压器振动烈度会出现突然增大或减小的现象；变压器悬挂位置对自身振动烈度影响较弱，悬挂越靠近中部，振动烈度会稍微降低。

综上分析可知：变压器悬挂于车体中部能明显改善180 km/h以上速度车辆中部舒适性。但在实际工程中，车下设备舱内空间有限，通过改变变压器悬挂位置提升车辆舒适性可行性不大。因此后续研究中只考虑变压器悬挂于车辆中部工况。

变压器悬挂频率也是影响车辆系统振动特性的重要因素。文中引入变压器悬挂频率比的概念，悬挂频率比定义为变压器沉浮模态频率与车体垂向弯曲频率的比值，文中变压器悬挂频率比选定为0.4～2.5。

悬挂频率比对车辆舒适度指标影响趋势见图10。由图可知：当车速超过150 km/h，悬挂频率比对车辆端部舒适度的影响开始凸显；在不同速度、悬挂频率比条件下车辆端部舒适度指标会出现峰值，当悬挂频率比大于1.4，端部舒适度不再随悬挂频率比变化而变化；车辆中部舒适度指标变化趋势有所不同，悬挂频率比逐渐增加，中部舒适度指标呈现出先减小后增大的趋势，并在悬挂频率比取0.7时出现谷值，当悬挂频率比大于1.4，中部舒适度不再随悬挂频率比变化而变化；尤其当速度高于200 km/h，悬挂频率比大于1.1时车辆中部舒适度指标增加明显。

变压器振动烈度变化趋势见图11。由图可知：在某些速度区间(如160～240、290～310、340～380 km/h)变压器振动烈度在特定悬挂频率比下会超过4.5 mm/s；整体看来，变压器振动烈度随悬挂频率比增大逐渐降低，当速度高于120 km/h，变压器振动烈度会在悬挂频率比取0.7时出现峰值，当变压器悬挂频率比大于0.9可以避免振动烈度出现峰值的现象。

图10 变压器悬挂频率比对车辆舒适度指标影响

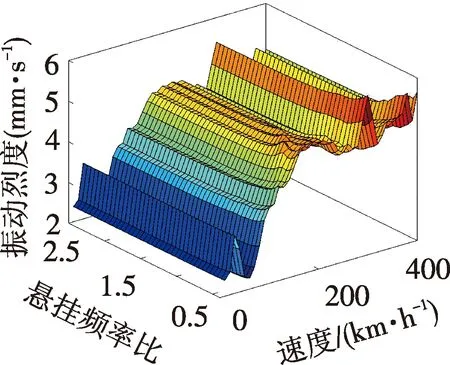
图11 变压器振动烈度

综上分析可知：变压器悬挂频率比对车辆舒适度影响明显，悬挂频率比超过1.4，车辆中部、端部舒适度不再随着频率比变化而变化；速度高于200 km/h，悬挂频率比大于1.1，中部舒适度指标明显上升；当变压器频率比大于0.9，可以避免变压器振动烈度出现峰值的现象。为了同时保证车辆舒适度和设备振动烈度，最终确定变压器悬挂频率比为0.9～1.1。

车辆舒适度指标计算见图12,变压器振动烈度随悬挂阻尼比的变化关系见图13。

图12 设备悬挂阻尼对比车辆舒适度指标影响趋势

图13 变压器振动烈度

由图可知：变压器的悬挂阻尼比对车辆中部、端部舒适度指标，以及自身振动烈度影响均不明显。通过改变悬挂阻尼比提升车辆舒适性和改善设备振动水平意义不大。

5 结论

本文建立了高速列车-变压器耦合系统动力学模型，利用数值积分方法对车辆系统振动响应进行了求解，并计算了在轮轨激励和变压器自身激励共同作用下车辆的舒适度指标和变压器的振动烈度，最后根据车辆系统振动指标的变化趋势对变压器悬挂参数进行了选择，研究结论如下：

(1) 变压器悬挂于车体中部能明显改善车辆中部舒适性，且变压器悬挂阻尼比对车辆舒适度指标和设备振动烈度影响不明显。

(2) 变压器悬挂频率比能明显影响车辆的乘坐舒适性，当悬挂频率比大于1.4，车辆端部、中部舒适度指标不再随悬挂频率比变化而变化。最终确定变压器悬挂频率比为0.9～1.1，该条件下车辆既能拥有较好的乘坐舒适性，变压器也能拥有较好的振动水平。

(3) 变压器的悬挂阻尼比对车辆中部、端部舒适度指标以及设备振动烈度影响均不明显。通过改变变压器悬挂阻尼比来提升车辆乘坐舒适度和改善设备振动水平意义不大。