基于点线一体化的高速铁路通过能力计算研究

王宇强，方 波，魏玉光，韩学雷

(北京交通大学 交通运输学院，北京 100044)

近年来我国高速铁路(以下简称高铁)发展迅速，对准确掌握和评估高铁通过能力提出了更高要求，高铁通过能力计算及相关理论研究已成为铁路运输组织领域的热点。与其他国家相比，我国高铁运输组织模式复杂多样且自成体系，然而已有的通过能力计算方法或借鉴既有线[1]，或直接采用国外算法，方法复杂且针对性不强。本文将车站虚拟为区间，提出了车站区间一体化的高铁通过能力计算新方法。

1 研究高铁通过能力的新思路

1.1 现有计算方法

高铁通过能力是指在一定的高铁基础设施运用标准、列车运行技术装备运用指标和旅客列车开行方案条件下，一个客流区段在列车运行图有效时间内可放行的最大列车数或列车对数，一般按区段或方向确定。需分别计算区间通过能力和车站通过能力后，取其中较小值作为高铁通过能力。

高铁区间通过能力计算方法主要包括扣除系数法、平均最小列车间隔法、日本的山岸式计算法和计算机模拟法4种[2]。文献[3]研究了扣除系数法在高铁中的应用，分析了不同等级列车越行区段选取方法和列车的共用停站分组方法，在此基础上提出了基于低等级列车扣除系数与列车停站扣除系数的高铁能力计算方法。但扣除系数法由普速列车发展而来，并不适用于高铁高质量的运输组织模式，且对于扣除系数的选择需要很高的精确度，增加了计算难度。对于平均最小列车间隔法，文献[4]在高铁无越行区段上，根据对其标准通过能力和使用通过能力及使用通过能力弹性系数的定义，提出基于列车运行图平均最小列车间隔时间的区段标准通过能力和考虑列车运行图缓冲时间的区段使用通过能力的计算方法；文献[5-6]系统介绍了平均最小列车间隔法。对于日本山岸式，文献[7]给出了其计算方法及适用环境。但平均最小列车间隔法和日本山岸式只考虑了本线列车，显然不适用于我国复杂的网状运输模式。对于计算机模拟法，文献[8-10]分析了高铁通过能力的影响因素，提出了新的通过能力计算模型，通过计算机编程求解模型，最后结合实际客流区段对方法进行了验证。但计算机模拟法的计算结果中可行解较多，最优方案比选困难。

在高铁车站通过能力计算方面，主要采用分析计算法、图解法和计算机模拟仿真法，其中计算机模拟仿真法的本质就是图解法。对于分析计算法，文献[11]给出了客运站到发能力、咽喉通过能力、客车整备场通过能力的利用率计算公式和方法。但其公式中参数查定的方法较为复杂。对于图解法，由于其工作量大且难度大已被计算机模拟法取代。对于计算机模拟仿真法，文献[12]提出不同层次车站理论通过能力的计算方法，利用压缩加密模型和自行开发的仿真系统进行案例验证；文献[13]运用计算机仿真的方法，将到发线和咽喉区的作业相互协调配合，计算出一天繁忙时段车站所能接发列车的总和，即车站高峰小时通过能力。虽然计算机模拟仿真法计算精度高，但随着车站规模的增大解空间会相应增大，对系统的求解效率有很高的要求。

1.2 基于点线一体化的高铁通过能力计算思路

可以看出，现有计算方法都没有把车站和区间的通过能力统筹考虑，导致计算过程复杂，可实施性差。高铁动车组列车在车站作业简单，主要为列车始发、终到、通过、待避停站、为完成旅客乘降作业的停站和一些跨线列车作业，均与区间运行过程直接相关，如把列车在车站的作业过程简化后用运行线表示，那么车站就可以虚拟为一个有长度的区间，则高铁“车站-区间-车站…”的布局模式就变成“虚拟区间-区间-虚拟区间…”的连续多个区间分布形式，按照通过能力理论，分析得到可能成为高铁能力限制的区间，分别计算这些区间的通过能力后，通过比较取其中最小者为限制区间通过能力即该区段的通过能力。由于高速列车在车站的开行模式决定了列车在区间的开行模式，因此高铁能力一般受限于车站而不是区间，也就是车站的通过能力决定着整个区段的通过能力。因此，计算高铁通过能力就转化为求各车站即虚拟区间的通过能力，采用平均最小列车间隔时间法计算虚拟区间通过能力，并确定限制区间，即为该区段的通过能力。基于点线一体化的高铁通过能力计算方法的步骤为：

(1)车站虚拟化。将车站转化为虚拟区间后，分析不同列车在虚拟区间的运行线，有越行关系的列车要进一步虚拟运行线。

(2)最小列车间隔时间计算。把两两相邻的追踪列车作为虚拟区间运行图的基本结构单元，分析不同列车组合在虚拟区间的最小列车间隔时间。

(3)虚拟区间通过能力计算。在现有列车开行方案条件下，分析高速列车数量和种类，求平均最小列车间隔时间，计算有效作业时间内可放行的列车对数。

(4)确定限制区间。将该区段各个大型客运站虚拟化为区间后分析计算得到通过能力最小的车站，为该区段的通过能力。

2 基于点线一体化的高铁通过能力计算方法

2.1 虚拟区间的定义

为方便处理列车停站、越行以及其他作业和跨线列车对高铁通过能力计算的影响，简化运行图结构，将车站虚拟为一个有长度的区间，那么列车各项作业就会转换成列车在此区间内不间断运行的过程，从而将复杂的车站通过能力求解转化为简单的区间通过能力求解，简化求解过程，提高求解精度。本文将此区间定义为虚拟区间。

虚拟区间建立过程见图1。线路上有A、B、C 3个车站，假设列车1、2、3、4为相同速度类型的列车，其中列车1、2、3在B站有停车作业，列车4直接通过B站，且列车4会在B站越行列车3，如图1(a)所示。以原B站为中心线，可以将有列车停车作业的B站虚拟为一个虚拟闭塞分区BB′，如图1(b)所示。此时列车1′、2′、3′变成不停站直接通过BB′区间，但是通过该虚拟区间的虚拟速度也将降低；而列车4′本来就是直接通过B站，故构建虚拟区间后，列车在此区间的运行时间为0，在运行图上表现为一段竖直线。

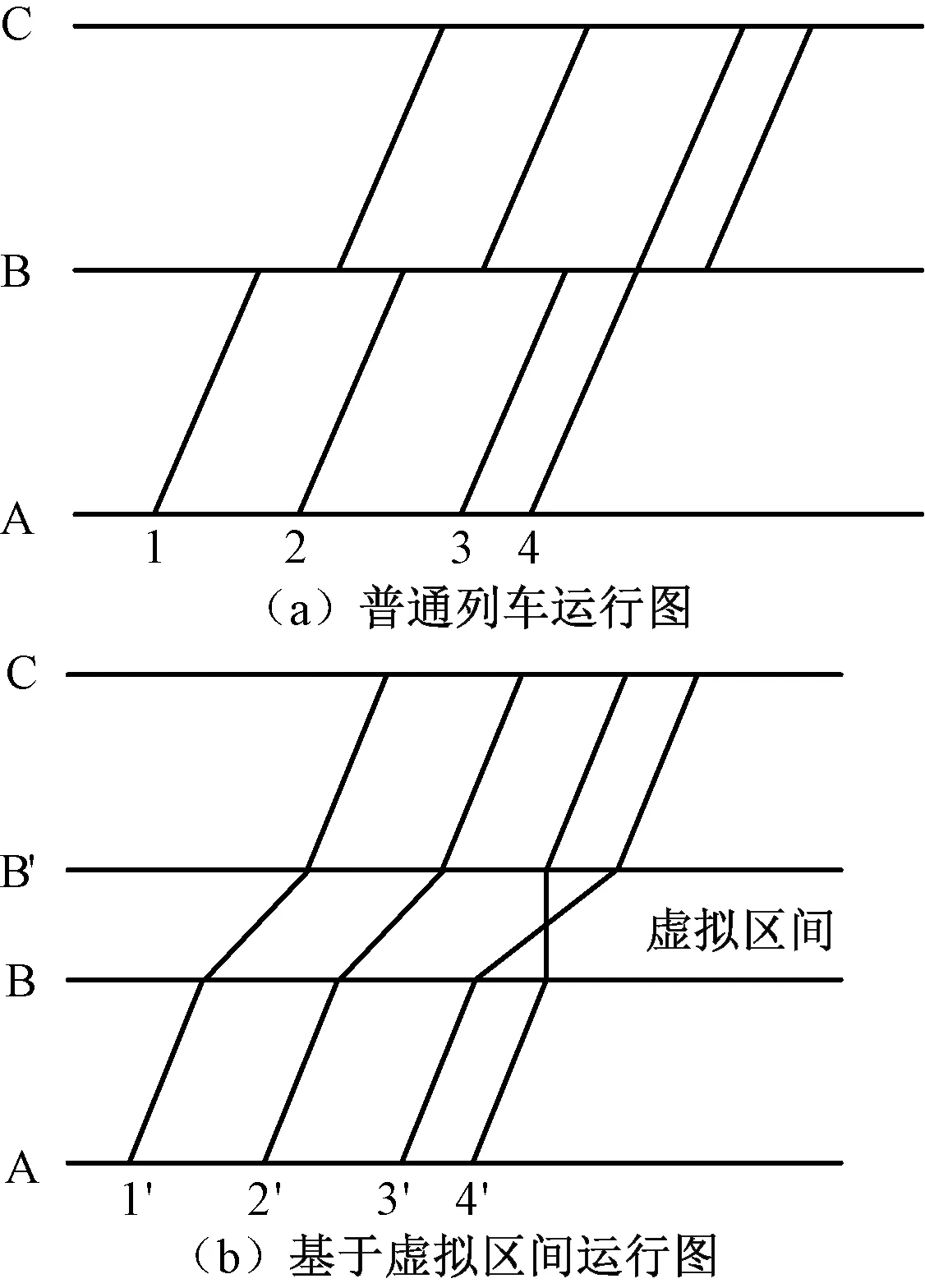
图1 虚拟区间的构建

为简化有越行情况的计算过程，提出虚拟运行线的概念，虚拟运行线的构建过程见图2。图2(a)为列车1、2在虚拟区间BB′应有的运行线，通过将列车1在虚拟区间BB′的运行线直接连接到列车2在B′C区间的运行线上，列车2在虚拟区间BB′的运行线直接连接到列车1在B′C区间的运行线上，就可以构建出两条新的虚拟运行线，即1′和2′，如图2(b)所示，此方法可在虚拟区间中将待避列车和越行列车视为两列前后追踪的停站列车。

所有类型列车在实际车站与虚拟区间的运行线见图3。

图2 有越行情况时虚拟运行线的构建

图3 车站虚拟化运行线

2.2 运行列车组分组及其间隔时间

若将两两相邻的追踪列车定义为运行列车组，则可视列车运行图由若干运行列车组的运行线组成。将虚拟区间两两相邻的列车也视为运行列车组，即可分析得到不同列车的组合及其在虚拟区间的最小列车间隔时间。

(1)“发到”和“到发”运行列车组

当第一列车为始发列车、第二列车为终到列车时，由虚拟区间运行线可得最小列车间隔时间为I发到，见图4。

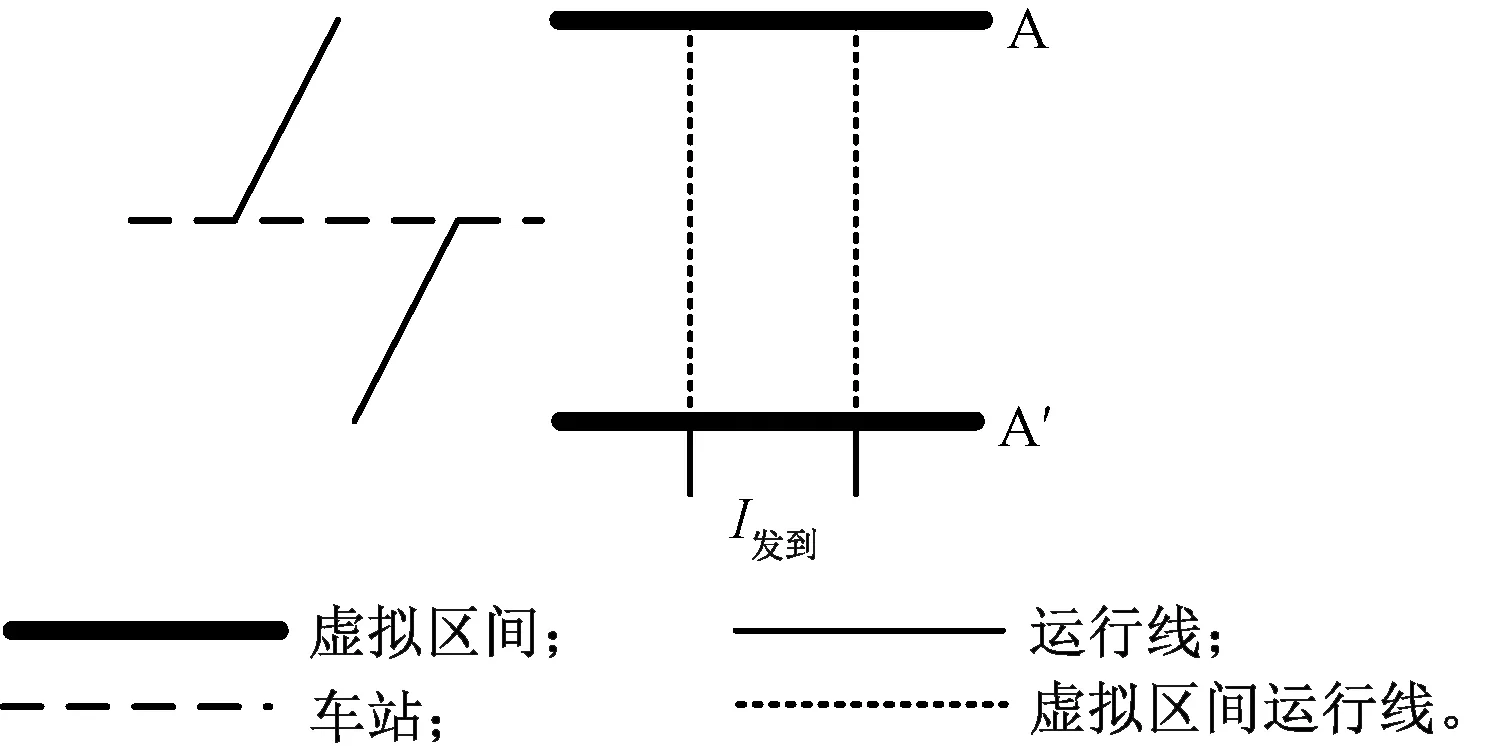
图4 “到发”运行列车组示意图

同理，当第一列车为终到列车、第二列车为始发列车时，虚拟区间运行线仍和图4类似，但最小列车间隔时间为I到发。

(2)“发通”和“通发”运行列车组

当第一列车为始发列车、第二列车为通过列车时，由虚拟区间运行线可得两列车最小列车间隔时间为I发通， 见图5。

图5 “发通”运行列车组示意图

同理，当第一列车为通过列车、第二列车为始发列车时，虚拟区间运行线仍和图5类似，但最小列车间隔时间为I通发。

(3)“发发”运行列车组

当两相邻列车在车站都是始发列车时，由虚拟区间运行线可得最小列车间隔时间为I发，见图6。

图6 “发发”运行列车组示意图

(4)“发停”和“停发”运行列车组

当第一列车为始发列车、第二列车为停站列车时，由虚拟区间运行线可得最小列车间隔时间为I发到，见图7(a)。同理，当第一列车为停站列车、第二列车为始发列车时，两列车虚拟区间运行线位置见图7(b)，此时的最小列车间隔时间为I发+t停,t停为停站时间，min。

图7 “发停”与“停发”运行列车组示意图

(5)“通到”和“到通”运行列车组

当第一列车为通过列车、第二列车为终到列车时，由虚拟区间运行线可得最小列车间隔时间为I通到，见图8。

图8 “通到”运行列车组示意图

同理，当第一列车为终到列车、第二列车为通过列车时，虚拟区间运行线仍和图7类似，最小列车间隔时间为I到通。

(6)“到停”和“停到”运行列车组

当第一列车为终到列车、第二列车为停站列车时，由虚拟区间运行线可得最小列车间隔时间为I到，见图9。

图9 “到停”运行列车组示意图

同理，当第一列车为停站列车、第二列车为终到列车时，两列车虚拟区间运行线位置和上图顺序相反，此时最小列车间隔时间为I发到+t停。

(7)“到到”运行列车组

当两相邻列车在车站都是终到列车时，由虚拟区间运行线可得最小列车间隔时间为I到，见图10。

图10 “到到”运行列车组示意图

(8)“通通”运行列车组

当两列车在车站都是通过时，由虚拟区间运行线可得最小列车间隔时间为I通，见图11。

图11 “通通”运行列车组示意图

(9)“通停”和“停通”运行列车组

“通停”运行列车组是指前行列车为通过列车，后行列车为停站列车，由虚拟区间运行线可得最小列车间隔时间为I通到，见图12。

图12 “通停”运行列车组示意图

同理，当第一列车为停站列车、第二列车为通过列车时，虚拟区间运行线顺序和上图相反，此时的最小列车间隔时间为I发通+t停。

(10)“停停”运行列车组

“停停”运行列车组是指前后行列车为追踪停站列车，由虚拟区间运行线可得最小列车间隔时间为I到，见图13。

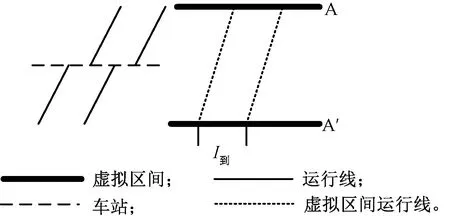
图13 “停停”运行列车组示意图

(11)待避越行列车组

越行列车和待避列车通过构造其虚拟运行线，可看作在虚拟区间中两列追踪的通过列车，方便后续的待避越行列车组的处理，见图14。此时由虚拟运行线可得最小列车间隔时间为I到通。

图14 待避越行列车组示意图

(12)“通越”运行列车组

此处的“通越”运行列车组是指第一列车为通过列车，第二列车为待避越行列车组虚拟运行线的左半部分，也即待避越行列车组的第一条虚拟运行线，见图15。此时由虚拟区间运行线可得最小列车间隔时间为I通到。

图15 “通越”运行列车组示意图

(13)“停越”运行列车组

此处的“停越”运行列车组是指第一列车为停站列车，第二列车为待避越行列车组虚拟运行线的左半部分，也即待避越行列车组的第一条虚拟运行线，见图16。此时由虚拟区间运行线可得最小列车间隔时间为I发到+t停。

同理，当第一列车为“正接正发”的跨线列车时，与上述情况类似，但列车停站时间不一样，最小列车间隔时间为I发到+t停。

图16 “停越”运行列车组示意图

(14)“越通”运行列车组

此处的“越通”运行列车组是指第一列车为待避越行列车组虚拟运行线的右半部分，也即待避越行列车组的第二条虚拟运行线，第二列车为通过列车，见图17。此时由虚拟区间运行线可得最小列车间隔时间为I通发+I发通。

图17 “越通”运行列车组示意图

(15)“越停”运行列车组

此处的“越停”运行列车组是指第一列车为待避越行列车组虚拟运行线的右半部分，也即待避越行列车组的第二条虚拟运行线，第二列车为停站列车，见图18。此时虚拟区间运行线的最小列车间隔时间为I通发+I发到。

图18 “越停”运行列车组示意图

图19 “反接正发”跨线列车和左半待避越行列车组示意图

同理，当第二列车为“正接正发”的跨线列车时，与上述情况完全类似，最小列车间隔时间不变，仍为I通发+I发到。

(16)“反接正发”跨线列车和左半待避越行列车组

(17)“正接正发”跨线列车

跨线列车正向接入，正向发出，与普通的本线停站列车类似，但其停站时间与本线列车不同。有“正接正发”跨线列车时的运行列车组见图20。

图20 有“正接正发”跨线列车的列车组

根据上图将车站虚拟区间化之后即可分别得到对应的虚拟区间运行线，见图21。

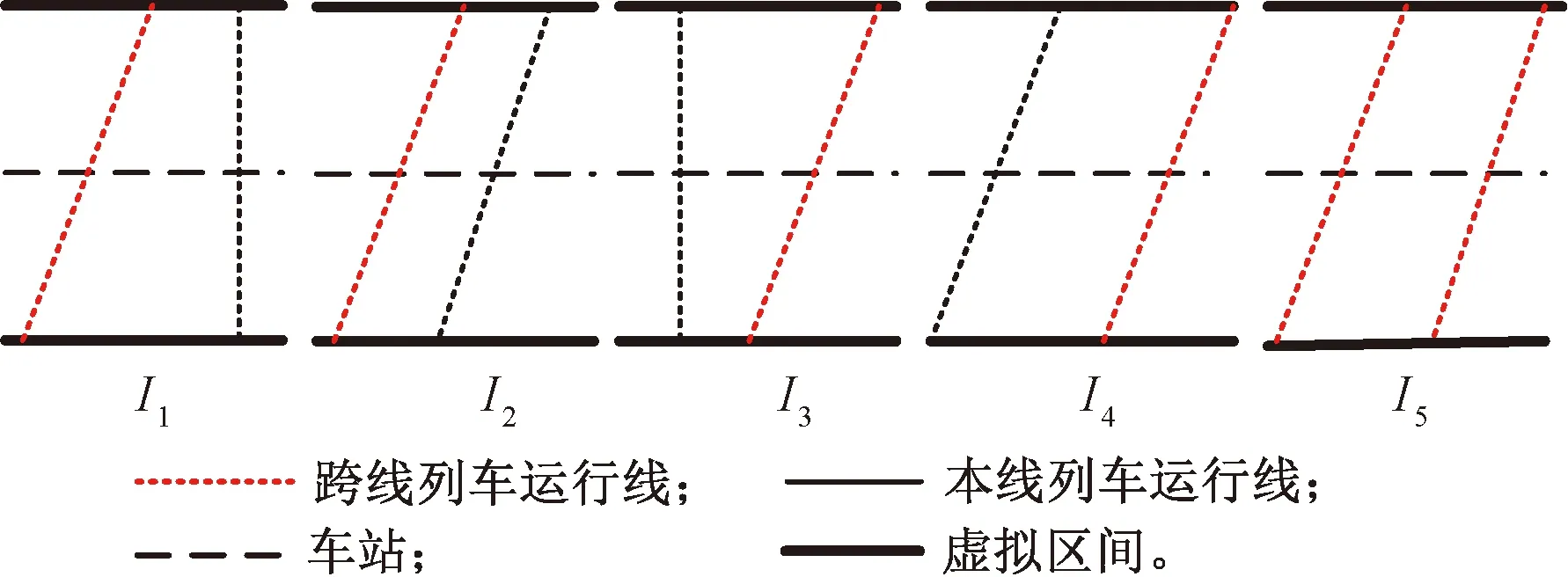
图21 有“正接正发”跨线列车的列车组虚拟区间运行线

(18)“反接正发”跨线列车

跨线列车反向接入，正向发出，“反接正发”跨线列车的停站时间也与“正接正发”跨线列车的不同，需要注意区分。有“反接正发”跨线列车时的运行列车组见图22。

图22 有“反接正发”跨线列车的列车组

根据图22将车站虚拟区间化之后既可分别得到上图所对应的5种情况的虚拟区间运行线，见图23。

图23 有“反接正发”跨线列车的列车组虚拟区间运行线

由图23中列车运行线可知，相邻跨线列车和本线列车的车间隔时间分别为

(19)相邻“正接正发”和“反接正发”跨线列车

这种情况是指两相邻列车均为跨线列车，且一列为“正接正发”，另一列为“反接正发”。两种跨线列车组合时的运行列车组见图24。

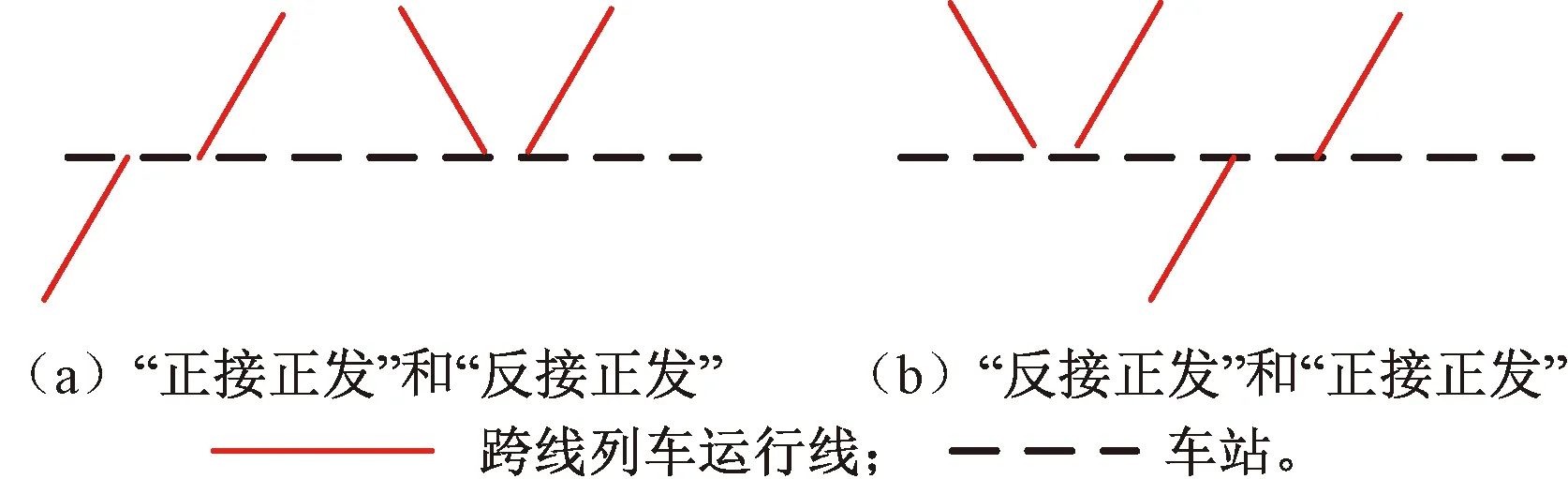
图24 “反接正发”和“正接正发”跨线列车的列车组

根据图24将车站虚拟区间化之后即可分别得到所对应的2种情况的虚拟区间运行线，见图25。

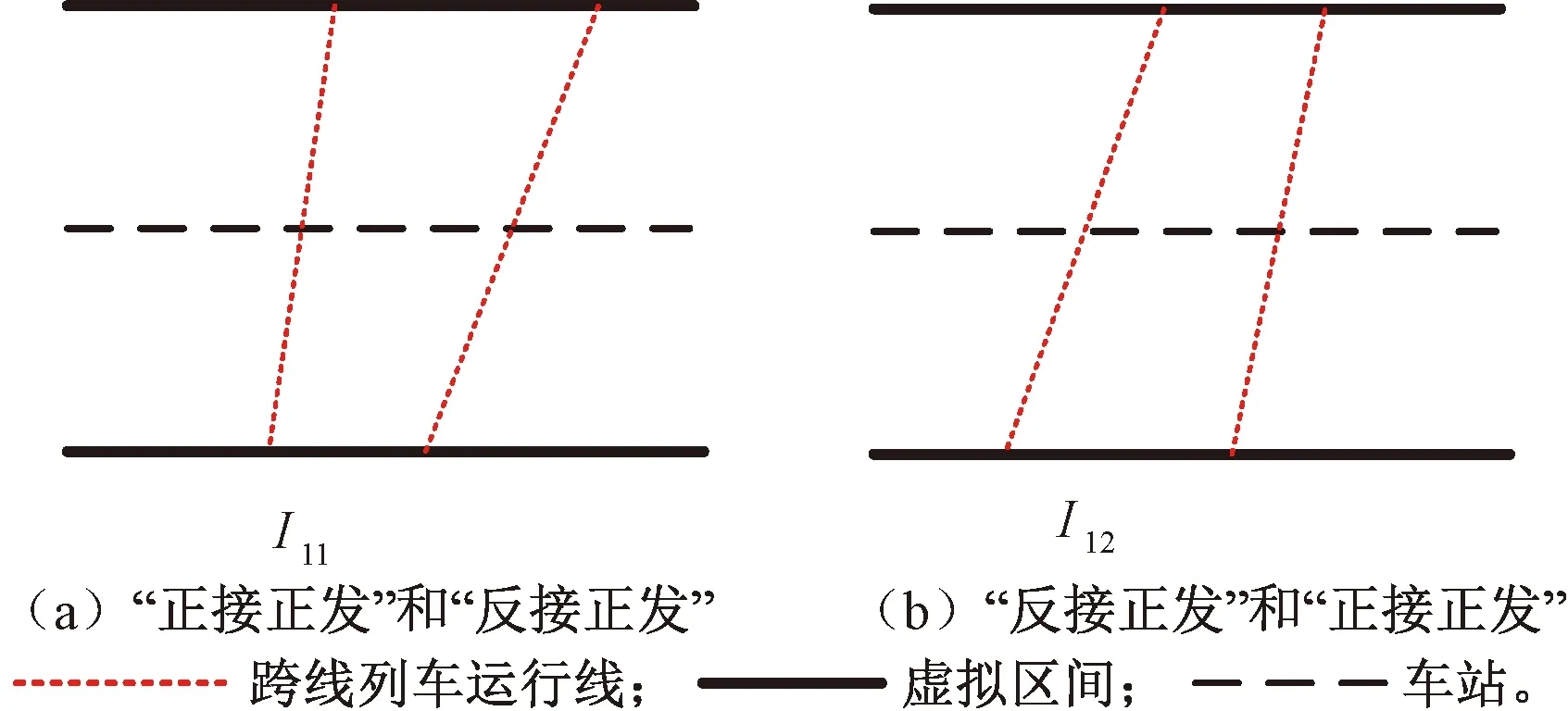
图25 “反接正发”和“正接正发”跨线列车的列车组虚拟区间运行线

由图25中列车运行线可知，跨线运行列车组的间隔时间分别为

因篇幅有限只考虑了以上几种列车组类型，如果有需要的话其他类型列车组依然可根据此规律表示。

由此可知将车站虚拟为一个区间后，通过上述一一对应的关系确定了各列车组在虚拟区间的运行线与相应的列车间隔时间，在今后的运行图铺画中可以直接使用该方法，在能力计算时可以直接使用新的列车间隔时间，也方便了对跨线列车的处理，使运行图结构更加简单、明了，能力的计算结果也更加符合实际情况。

2.3 虚拟区间通过能力计算

将车站虚拟为区间就可以使用最小列车间隔法来求解虚拟区间的通过能力，即车站的通过能力。N1为根据运行图查定的某高铁车站单方向一日接发的全部列车数，其中n1、n2、n3、n4和n5分别为本线列车中始发列车、终到列车、通过列车、仅停站列车和待避列车数；n6为跨线列车中“正接正发”列车数；n7为“反接正发”列车数。对于一些本线列车的“反接正发”和“正接反发”作业，该类情况一般出现在始发列车或终到列车中，情况较少，且与跨线列车造成的影响基本相同，所以将这些列车归为跨线列车相应的类别中进行计算。

则在运行图上出现上述某种列车的概率pi为

(1)

式中：i为列车种类组序号。

出现上述某种运行列车组的概率pij为

(2)

式中：i为运行列车组第一列车的列车种类组序号；j为运行列车组第二列车的列车种类组序号。

则运行列车组中某种列车组数nij为

(3)

不考虑其他因素，所有运行列车组在运行图上占用虚拟区间的总时间B为

(4)

式中：Iij为i类列车与j类列车的最小列车间隔时间，min。

当考虑各方向跨线列车因切割车站咽喉而对研究方向列车占用虚拟区间总时间影响时，列车组在运行图上占用虚拟区间的总时间B′为

(5)

式中：s为各方向跨线列车总类数，s≥1；xki表示k类跨线列车是否影响i类列车占用虚拟区间时间，xki=1为影响，xki=0为不影响；tki为k类跨线列车影响i类列车时增加的占用虚拟区间时间，min。

(6)

由于各个车站的运营时间不同，所以引入f为高铁站一天的运营时间所占总时间的比例，那么虚拟区间通过能力，即车站通过能力N通为

(7)

式中：T为一天的时间，取1 440 min。

根据高铁通过能力理论与本文提出的虚拟区间的概念，高铁区段的能力限制区间为通过能力最小的虚拟区间，通过使用上述高铁虚拟区间的能力计算方法，可以计算出该区段各大型客运站所对应的虚拟区间的通过能力，选其中最小者即为该区段的通过能力。

3 京沪高铁通过能力计算

京沪高铁是我国重要的高铁通道，计算其能力有重要意义。由于高铁通过能力的限制区间在大型客运站对应的虚拟区间，分析京沪高铁所经过的车站可知京沪高铁能力的限制点可能为济南西站、南京南站和徐州东站等，由于篇幅有限，以徐州东站为例计算其对应的虚拟区间通过能力，徐州东站站场示意图见图26。

(1)基础数据

以京沪高铁徐州东站2018年5月某天下行方向接发的高铁列车数据为例，各类高铁列车数量为：本线列车105列，其中始发列车2列，终到列车4列，通过列车22列，仅停站列车69列，待避越行列车8列；跨线列车54列，其中“正接正发”列车38列，“反接正发”列车16列。

各种列车间隔时间见表1。

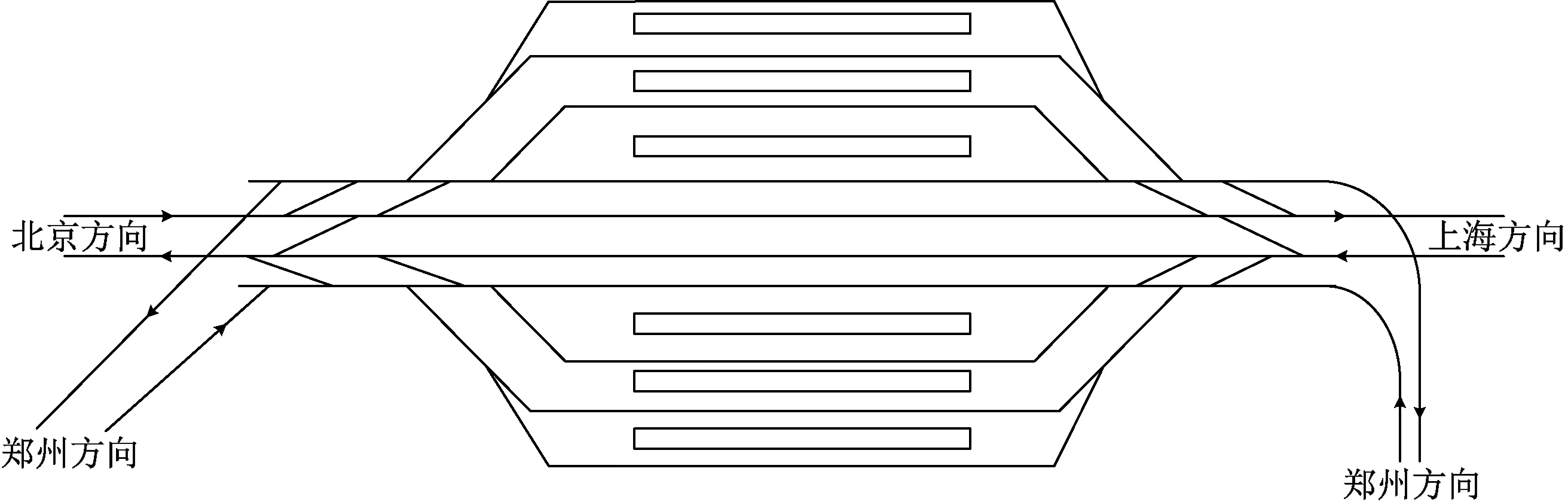
图26 徐州东站站场示意图

表1 各种列车间隔时间 s

各类列车停站时间为：本线列车3.11 min，“正接正发”跨线列车为4.74 min，“反接正发”跨线列车为8 min。

(2)计算过程

根据各列车数量可得出各列车出现概率：始发列车0.01，终到列车0.03，通过列车0.14，仅停站列车0.43，待避列车0.05；“正接正发”列车0.24，“反接正发”列车0.10。

根据第2节的各类列车组最小间隔时间与式(3)可得各类列车组的数量(存在四舍五入的情况)、各类列车组的最小间隔时间和各类列车组占用区间的时间，见表2。

表2 列车组数量及其时间间隔

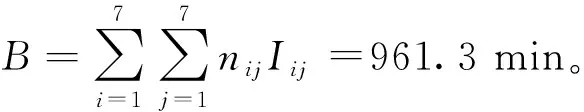
各方向跨线列车数为：郑州方向到上海方向中“反接反发”为4列，“正接反发”为6列；郑州方向到北京方向中“反接正发”为10列，“正接正发”为20列；北京方向到郑州方向中“反接正发”为6列，“反接反发”为3列；上海方向到郑州方向中“正接反发”为9列，“正接正发”为18列。取tki=1 min，则

根据徐州东站实际运营时间取f=0.7，由式(7)可得N通=163对，与实际运行159对相比，计算结果和实际情况较为吻合，说明计算结果比较准确可靠，同时也证明徐州东站通过能力利用率已经接近饱和状态。

再依此方法计算济南西站、南京南站等站的虚拟区间通过能力，选其中能力最小者即可求出京沪高铁的通过能力；同理计算郑州东站等站的通过能力就可求出郑徐高铁的通过能力。

4 结论

随着我国高铁网规模和客流需求的不断扩大，对准确掌握和充分挖掘高铁通过能力提出了更高的要求。本文提出将车站虚拟化的思想，通过构建车站的虚拟区间和相应列车的虚拟区间运行线，在平均最小列车间隔法的基础上给出了高铁通过能力的计算方法。现有计算高铁通过能力的方法普遍存在着将车站和区间割裂、不考虑跨线列车、对高铁能力缺乏进一步优化等问题，本文考虑了跨线列车对能力计算的影响、实现了车站与运行线的点线能力一体化计算，对于今后的高铁能力优化问题，虚拟区间的运用可以使模型结构更加简单，且将跨线列车也列入优化对象，使优化结果更加符合实际。