基于改进遗传算法的ATO速度曲线研究
2020-10-09董渠江聂莹莹郭彦宏
董渠江,聂莹莹,郭彦宏
(1.西南交通大学 信息科学与技术学院,成都 611756;2.中铁二院工程集团有限责任公司,成都 610031)
1 概述
目前国内的城市轨道交通事业正蓬勃发展,城轨运营需要大量的成本,电能消耗就其中之一。电能消耗中,牵引能耗占过半,因此,降低列车牵引能耗成为城轨节能优化的有效途径。同时随着智能控制算法的不断发展,相关算法在求解多目标优化问题中具有很强的优越性,以遗传算法为代表,许多学者将其应用于研究列车节能优化问题。
2 列车动力学模型与运行过程
2.1 列车动力学模型
对于列车的牵引计算,此处采用单质点模型进行分析。如图1所示,列车受力有:重力G,牵引力F,阻力W和制动力B。

图1 列车动力学模型示意图Fig.1 Schematic diagram of train dynamics model
1)牵引力与制动力
一般情况下,确定机车型号的牵引力与速度,手柄级位关系如公式(1)所示,制动力与速度和手柄级位关系如公式(2)所示。

其中v为速度,t为当前的手柄档位。
2)列车阻力
列车阻力通常采用如(3)所示经验公式。
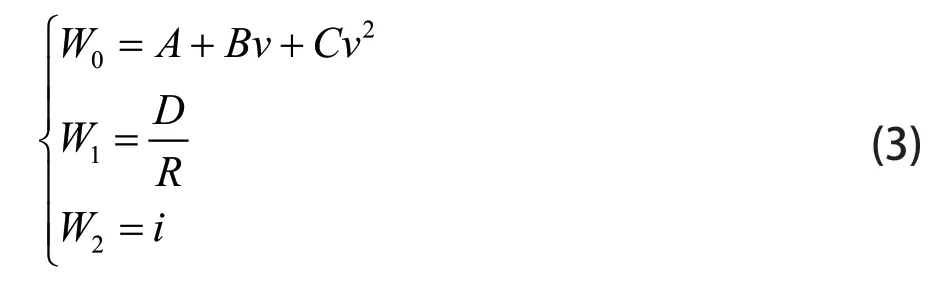
其中,W0是单位基本阻力(N/kN),A,B,C为阻力系数,常取经验值,W1为单位曲线阻力(N/kN),D为常数,取值600,R为曲线半径(m)。W2为单位坡度阻力(N/kN),i为坡度。
列车单位阻力为:
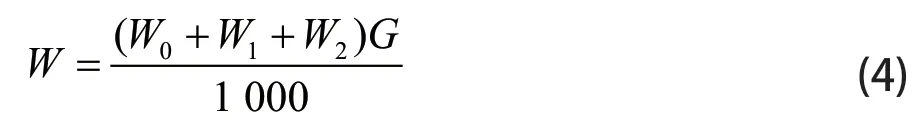
列车所受合力为:

2.2 列车运行过程
如图2所示,列车在区间运行过程中一般包含4种工况。
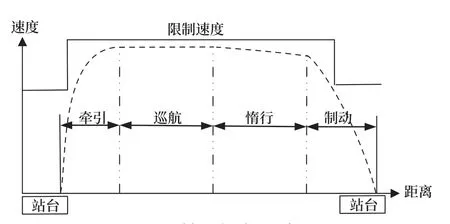
图2 列车运行过程示意图Fig.2 Schematic diagram of train operation
加速牵引:列车处于加速运行状态,列车受牵引力和阻力作用。
匀速巡航:列车处于匀速运行状态,列车所受合力为0。
惰行阶段:列车不牵引,也不制动。
制动阶段:列车在此过程受到制动力和阻力共同作用。
3 算法设计
3.1 染色体设计
如图3所示,染色体为工况转换点的牵引制动级位与距离点的组合,即(ti,si),ti为第i个工况转换点的牵引制动档位,si为第i个工况转换点的位置。
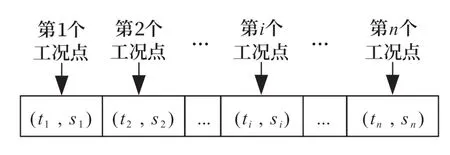
图3 染色体结构设计示意图Fig.3 Design of chromosome structure
3.2 基因值约束
种群初始化时,基因值因不同工况有如公式6所示的基因值约束。

其中,Timin,Timax分别代表第i个工况转换点档位的最小值与最大值,Simin,Simax分别代表第i个工况转换点位置的最小值与最大值。
结合工况阶段,基因值约束如表1所示。Sr为实际距离,Lb为列车最大制动距离。取列车在最大下坡的最大常用制动距离加一定余量。Ti取值1-10,代表牵引档位,11-20为制动档位,0为不牵引也不制动。
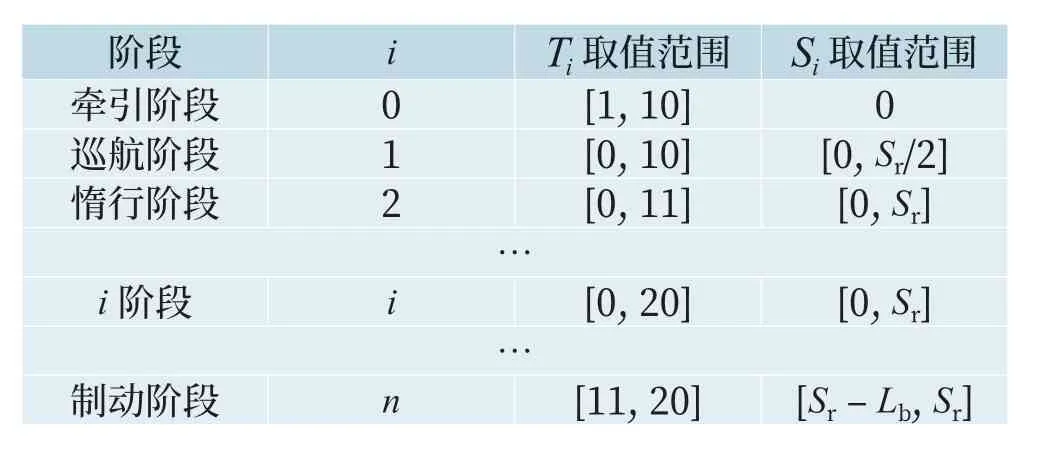
表1 基因值取值范围Tab.1 Range of the values of genes
3.3 适应度函数
1)适应度函数

适应度由多个评价函数组成。如公式(7)所示,其中a,β,μ,δ为各评价函数权重,Fs为停车精度评价函数,Ft为准时性评价函数,Fe为能耗评价函数,Fv为触发紧急制动限速的评价函数。
2)通用评价模型

公式(8)为评价函数的通用模型。其中Ei为每个对应指标(Es,Et,Ee,Ev,)的评价函数。Ni为使评价函数保持相同数量级的归一化指数,当评价函数值为1时,认定指标在误差范围内。
3)评价函数

公式(9)为停车精度评价函数。其中es为可接受最大停车误差(m),其值取0.25 m。Sr为区间距离(m),Sc实际运行距离(m)。
公式(10)为准时性评价函数。其中et为可允许时间误差(s),取值为计划运行时间的5%,Tr为计划运行时间(s)。Tc为实际运行时间(s)。
公式(11)为能耗评价函数。其中ee为运行1 km的标准牵引能耗(kW·h),此值与具体车型、线路等因素均有关,根据文献[1-2]及本文数据,此值取8。Er为计算的牵引能耗(kW·h),计算方式如公式(12),其中Fi为距离i处的牵引力(kN)。
公式(13)为限速评价函数。其中Vi为速度(km/h)。Noverv为运行过程中,每当出现超速情况,进行自增计数。
3.4 变异策略
进化过程中,个别优秀个体的迅速繁殖会导致种群多样性丧失,从而出现过早收敛的问题[3]。根据文献[4],此处采用熵来评价种群多样性,如公式(15)定义熵Et。

当种群熵为0时,此时种群的所有个体处于以下阶段之一。
阶段1:全局最优;
阶段2:较小概率进化至全局最优的局部最优;
阶段3:较大概率进化至全局最优的局部最优。
此时引入阶段评判准则:若fs或ft大于其最大值的80%,则认为种群处于阶段3;否则种群处于阶段2。变异策略根据评判准则,分为全局搜索策略和局部搜索策略。当种群处于阶段3时,执行局部搜索策略。若处于阶段2,执行全局搜索策略。
3.4.1 全局搜索策略
针对种群多样性丧失,变异操作可以显著地提高种群的多样性[4]。但是,简单提高变异概率,易造成算法的局部搜索能力被破坏,得不到最优解。因此,在全局搜索阶段,采取一种基于熵的变异算子来保持种群多样性和全局搜索能力,第t代的变异概率为:

其中,pt为第t代的变异概率,p0为变异率上限,取值0.5,Et为第t代的熵值,Emax为熵的最大值,pr为控制pt的缩放因子,取值0.4。
3.4.2 局部搜索策略
虽然全局搜索阶段的变异策略提升了算法的全局搜索能力和种群的多样性,但仍会出现局部最优且熵值为0的情况。此时,种群处于阶段3,变异算子成为能否收敛至全局最优的唯一因素。故引入如下局部搜索策略。
对于距离si上牵引制动档位为ti的基因值,变异规则如下。
1)基因值变异范围
首先,为缩小算法后期的搜索范围,定义如图4的距离步长Δs和档位步长Δt,其取值如公式(17)所示。
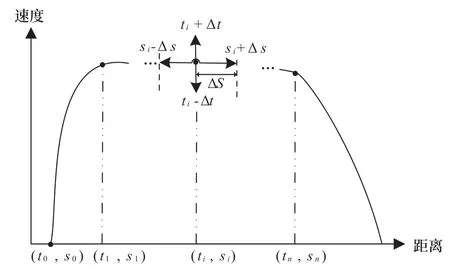
图4 变异范围示意图Fig.4 Range of mutation
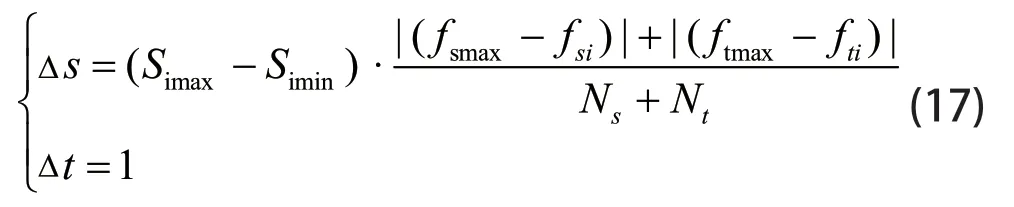
其中,fsmax为停车精度最大适应度,fsi为当前个体的停车精度适应度。ftmax为运行时间最大适应度,fti为当前个体的运行时间适应度。
接着,计算基因值变异取值范围。
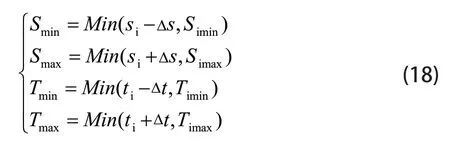
其中,Min为取最小值函数,[Smin,Smax]为第i个工况点距离变异范围,[Tmin,Tmax]为第i个工况点档位变异范围。

其中,Rand为随机函数,Sti为第i个工况点变异后的距离值,Tti为第i个工况点变异后档位值。
2)变异概率

其中,Nn为当种群进入阶段3的迭代次数计数器,Ngen为设置的迭代次数,Pr2为控制变异概率因子。
3.5 算法实现
算法步骤如下。
1)参数初始化。
2)计算种群适应度、熵值。
3)根据熵值以及适应度,以评价准则进行评判。
4)进行选择、交叉、自适应变异操作。进行轮盘赌选择与随机线性交叉操作,以随机变异方式进行变异操作。
5)生成备选种群,执行精英保留策略并生成下一代种群。
6)满足要求,则结束循环,输出结果;否则进入3)。
4 结果分析
4.1 仿真数据
采用C#编程实现了ATO速度曲线仿真计算软件,仿真软件中,列车的牵引制动数据基于文献[5],牵引特性数据如图5所示,制动特性数据如图6所示,列车仿真参数如表2所示。
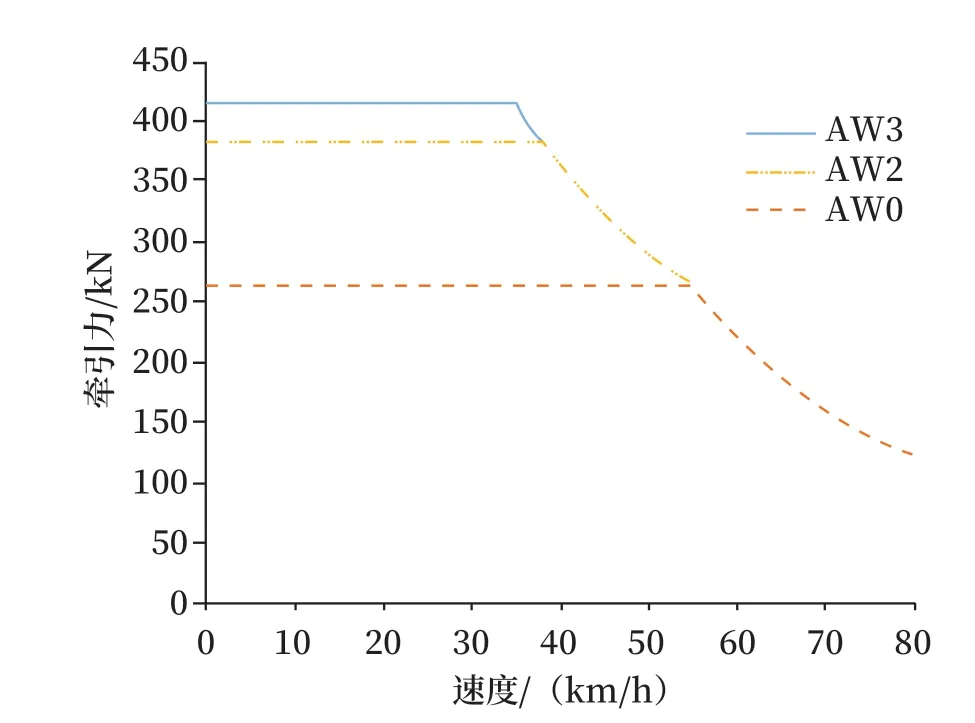
图5 牵引仿真数据Fig.5 Traction simulation data
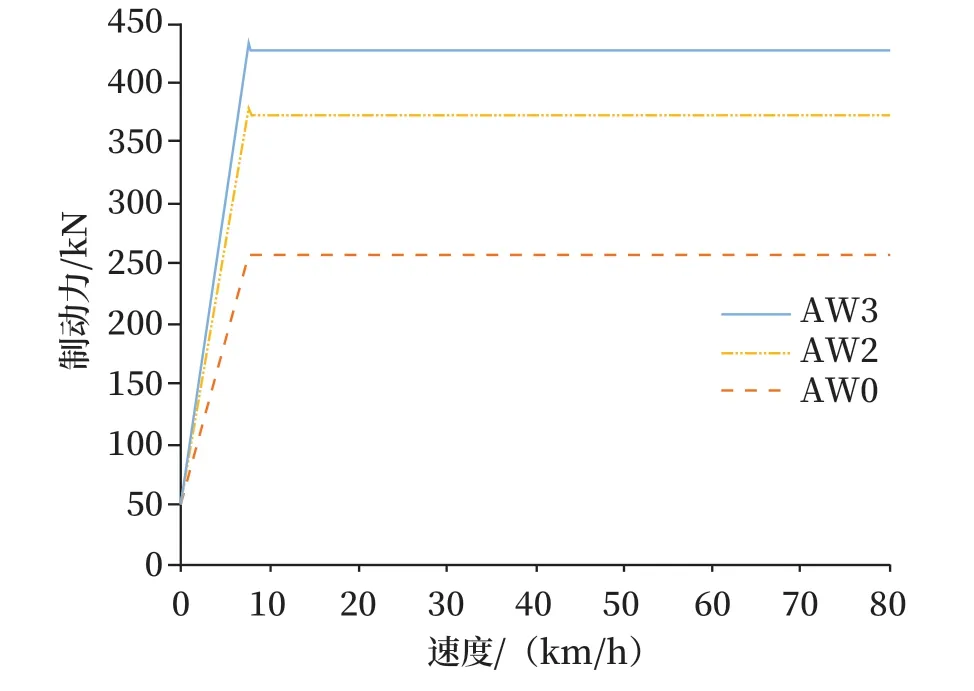
图6 制动仿真数据Fig.6 Braking simulation data
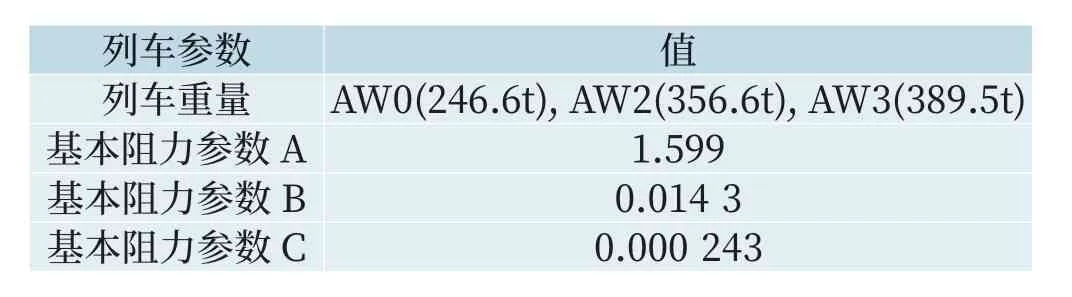
表2 列车仿真参数Tab.2 Parameters of train simulation
线路仿真数据如表3、4所示,评价函数权重取值如表5所示。
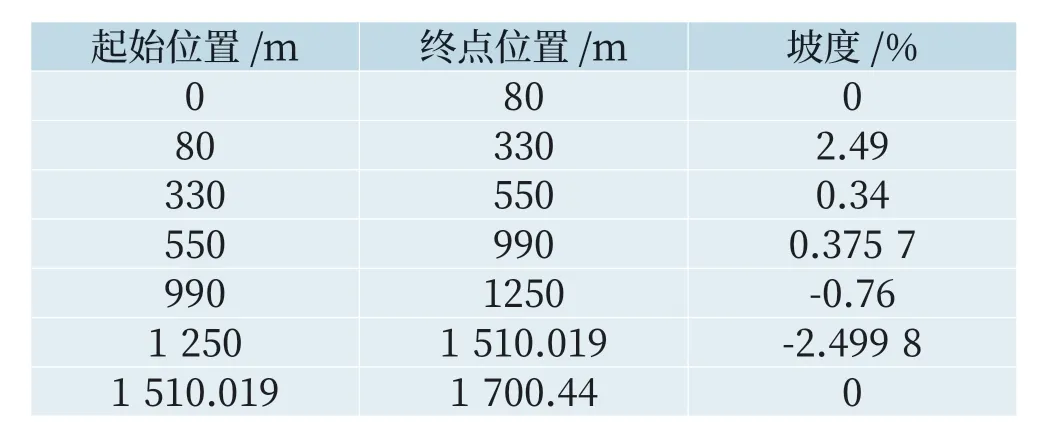
表3 线路坡度表Tab.3 Gradients of train lines
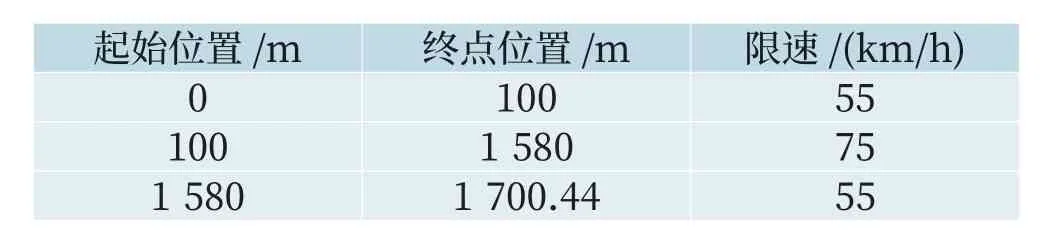
表4 线路限速表Tab.4 Speed limits of train lines
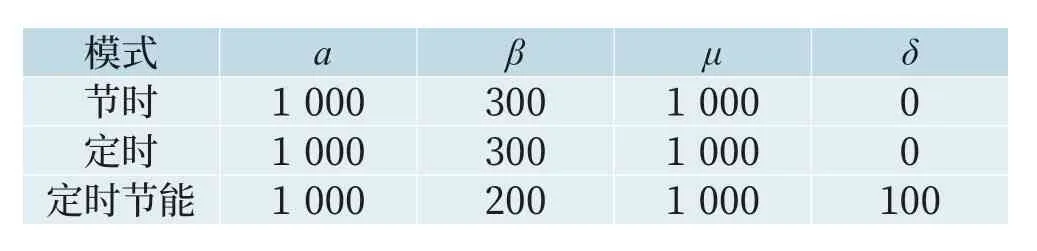
表5 评价函数权重取值表Tab.5 Values of evaluation weight function
4.2 案例结果
本文设置的区间运行时分为节时109 s,定时与定时节能为120 s,种群大小40,选择概率0.6,交叉概率0.7,列车载重389.5 t,工况转换点5,迭代次数500。标准遗传算法( Standard Genetic Algorithm,SGA)的交叉概率0.7,变异概率0.2。
1)与SGA对比结果
算法迭代500次,取改进GA不利情况(即阶段2时重新初始化种群)与SGA较好情况的适应度对比如图7所示。迭代100次前,改进GA的以较大概率全局寻优,其适应度低于SGA,同时避免了SGA易陷入局部最优的缺点。迭代次数超过100次以后,由于后期局部搜索策略,使其较大概率在较小范围进行局部搜索,局部搜索能力更强。因此,改进GA改善了SGA的全局搜索能力与局部搜索能力,同时工况点的基因值约束也减少改进GA的计算次数。
2)ATO速度曲线结果
节时、定时与定时节能3种模式下,ATO推荐速度曲线如图8所示,各项具体结果如表6所示。
由图8可知,节时模式工况为:牵引—巡航—制动,定时模式下为:牵引—巡航—惰行—制动。均符合对应模式下的牵引控制策略。而节能模式的工况为:牵引—惰行—制动,满足列车节能模式下尽可能惰行以达到节能目标的牵引控制策略[6]。
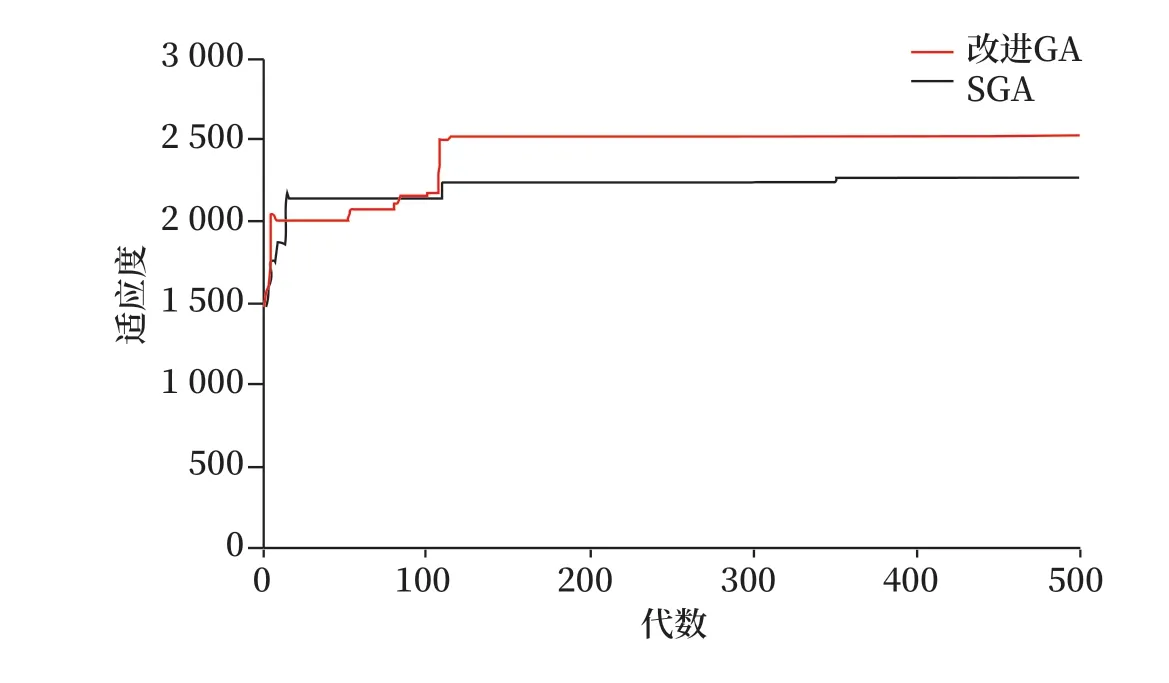
图7 改进GA与SGA适应度对比图Fig.7 Comparison of adaptiveness between improved GA and SGA
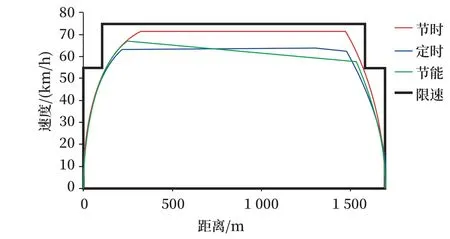
图8 3种模式下的ATO速度曲线Fig.8 ATO speed curves of the three modes
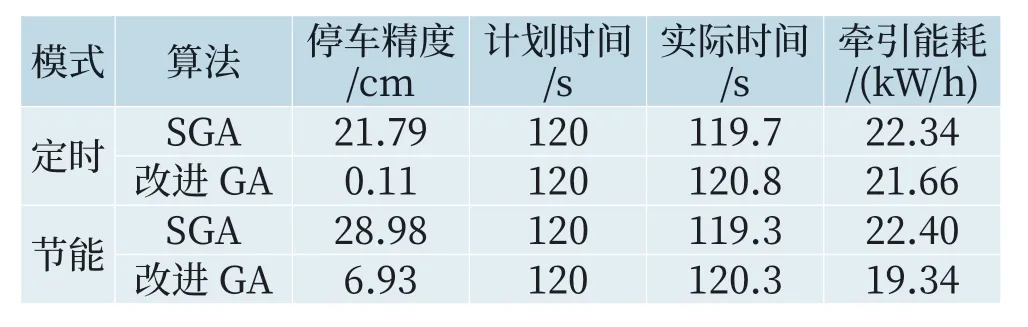
表6 不同模式的指标值Tab.6 Indices of diあerent modes
由表6中数据可知,改进GA在满足规定误差范围内,牵引能耗定时节能模式比定时模式少10.7%,说明该算法有效。
5 结论
本文提出了一种基于自适应变异策略的改进GA,用于计算ATO速度曲线。在满足规定区间运行时分指标,停车指标以及不超过限速指标前提下,结果符合列车节时、定时节能的牵引控制策略,且迭代次数更少,性能更优,对城轨列车节能具备一定的参考价值。
