善架“桥梁” 到达物理学习成功“彼岸”①

李庆国 姜业勇

(江苏省扬州市新华中学，江苏 扬州 225009)

高中物理概念、公式、规律多,很多同学觉得比较难学。其实只要我们善于思考,我们会发现很多物理知识、方法等都不是孤立的,都可以通过“桥梁”进行联系。这样的问题在高中物理中有很多，如涉及力和运动的关系问题,我们常称为动力学问题。动力学有两类基本问题：(1) 已知受力情况求运动情况；(2) 已知运动情况求受力情况。对于第(1)类问题,先由物体的受力情况求出合力,利用牛顿第二定律求出物体的加速度,再由运动学公式得到所求物理量,即知道了物体的运动情况。对于第(2)类问题,先根据物体的运动情况,运用运动学公式求出物体的加速度,再由牛顿第二定律求出物体受一个力或某几个力,即知道了物体的受力情况，具体流程如图1所示。

显然,不管是哪一类问题,确定物体的加速度是解题的关键,加速度是联系力学和运动学的“桥梁”。知道了这一点,遇到动力学问题时就不会孤立地仅从动力学角度考虑,也不会孤立地仅从运动学角度考虑,会通过加速度这一“桥梁”将力和运动进行联系,将知识点“化多为少”，很快找到解决问题的突破口,顺利解决问题。

又如，两带电体没有相互接触就会发生力的作用,原因是电荷A会在周围空间产生电场,电荷B处在A的电场中,会受到A的电场给它的电场力的作用。同样电荷B会在周围空间产生电场,电荷A处在B的电场中,会受到B的电场给它的电场力的作用。这个关系可用图2来表示，由此可看出,电场是不同带电体间发生作用的“桥梁”，只有搞清楚这个“桥梁”,对电荷间的作用才能理解得更透彻,把电场这种虽然看不见摸不着但又客观存在的物质直观呈现出来,对电场的理解更到位，同时为磁场的学习和理解打下很好的基础。

图2

再如，不同形式的能可以相互转化,但都必须通过做功这个过程,做功就是不同形式能量转化的“桥梁”,它们的关系可用图3来描述。搞清楚这个关系,对做功的实质以及功能关系的理解会更透彻。

图3

在高中物理中类似的情形还有很多，有些问题、知识间即使看起来没有联系,我们也可以构建“桥梁”,在看似不相干的知识之间建立联系,这样我们就不是一个个孤立地去学习,而是将物理知识连成片、织成网,学习就轻松得多了。“桥梁”可能是某个物理量,可能是某个物体,可能是某种方法,也可能是某种状态。那么，作为教师如何帮助或启发学生构造一个个“桥梁”呢？笔者对此进行了探讨,与同行分享。

1 运用二级结论构建“桥梁”，将看似无关的问题联系起来

例1:如图4所示,用皮带传动的两个轮子(皮带不打滑),r2=2r1,A点为轮子O1边缘上一点,B点为轮O2上某半径的中点,求A和B两点线速度大小之比和角速度之比。

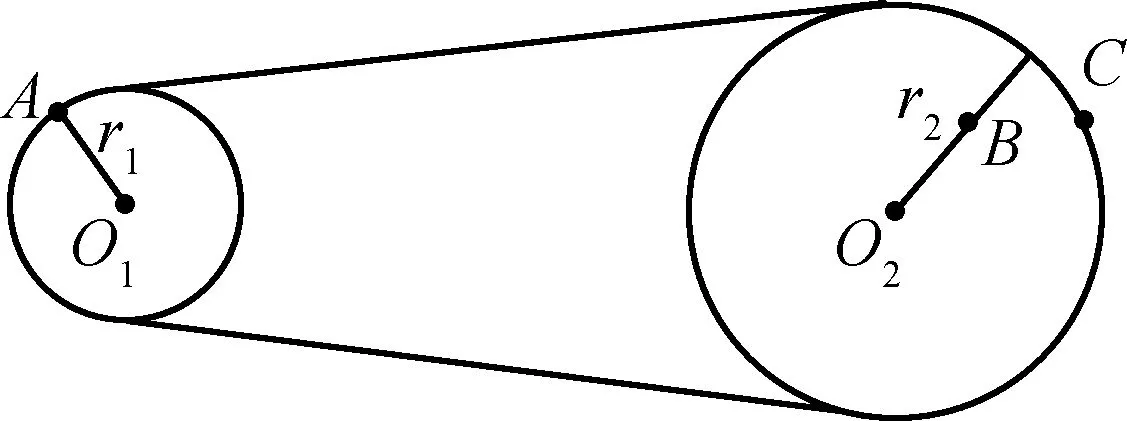
图4

解析：对于皮带传动,不同轮子边缘线速度大小相等，这是一个二级结论。A、B看起来没有联系,要直接找出A、B线速度和角速度的关系，似乎无从下手，但可以用上述结论构建A和B间的“桥梁”。如图4所示，在O2轮边缘上任取一点C,则有vA=vC。B、C同轮,ωB=ωC,由v=ωr可得：vC=2vB,综合可得：vA=2vB,进而可知ωA=2ωB。

若题目其他条件不变,只将A点改为轮O1上某半径的中点(图5),求A和B两点线速度大小之比和角速度之比。

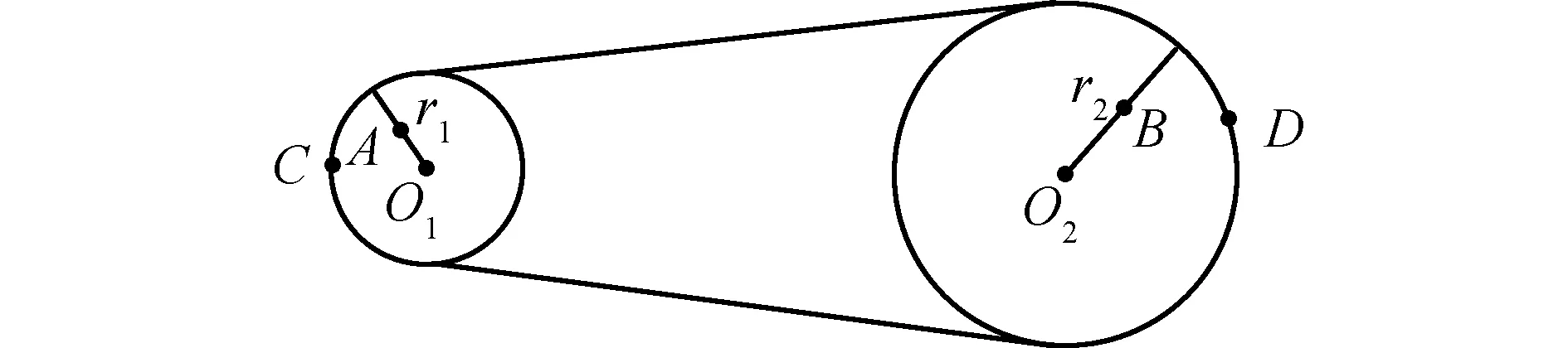
图5

讨论：和变化前相比,此时A、B看起来更无联系,但仔细思考仍可运用上述结论构建“桥梁”。在O1、O2轮边缘上各取一点C和D,A和C、B和D的线速度、角速度关系很好确定,再利用vC=vD可以顺利确定A、B两点线速度大小之比和角速度之比。

二级结论指的是教材中没有直接给出,依据有关的物理概念或规律,通过一定的演绎推理所得到的具有通用性意义的结论,或应用有关的物理概念或规律对典型的问题进行分析所得到的具有普遍性意义的结论。在遇到具体问题时,根据需要利用相应的二级结论构建“桥梁”，既能方便解决问题,又能加深对已有知识的理解。高中物理中有许多类似的二级结论,它可以是文字形式的描述,也可以是数学形式的表达。作为教师,一定要引导学生真正理解其成立的条件,理解二级结论的内涵和外延,千万不能死记硬背。只有这样,遇到实际问题时方能灵活运用,提升学生的物理学习能力。

2 架设物理与生活的“桥梁”，凸显物理知识的实用性

物理知识来自生活,但由于其抽象、难懂的特点,对学生的物理学习带来了一定的困难。为了解决这一问题,在物理教学中,应该搭建物理与生活的“桥梁”,用物理知识去指导生活,通过生活现象总结出物理原理。

2016年我校组织高二学生去“方特”游乐场,在坐旋转秋千时有学生说自己胆小不敢坐。教师告诉学生：秋千旋转后内侧吊椅离地高度小,外侧吊椅离地高度大,胆小的往内侧坐，再用圆周运动相关知识进行证明,但当时学生还是将信将疑。当他们从“方特”回来后说：老师你太厉害了！他们觉得物理真有用,对物理的兴趣也越来越浓。

还有一次年级举行拔河比赛,在比赛前的物理课上,教师对所教的两个班从物理方面进行了指导,比如说重心的高低、双脚的站位、身体的倾斜度等。比赛时又进行了现场指导,结果这两个班分别获得第一名和第二名。两个班学生非常高兴,真正体会到了“学有所用”,体会到了知识的力量。

在物理教学中通过生活现象建构物理概念,形成物理规律,再回归到生活中去,不仅可以使教学变得生动鲜活,避免了物理知识的空洞化,而且可以使学生深刻体会到生活中充满着物理原理,物理与社会生活是紧密相连的。

架设物理与生活的“桥梁”,就是引导学生会从物理的视角去看生活,生活中处处有物理,要有意识用所学知识去解释生活中的现象,指导生活和工作。在遇到各种现象时,能探究其中的物理原理,体验“物理发现”的过程,培养科学思维能力和创新能力，这样物理学习就会变为一种享受而不是负担。

3 架设“桥梁”，为学生设立问题解决的台阶

有些问题看似比较困难,但教师通过提问等方式给学生设立台阶,搭建“桥梁”,帮助学生顺利解决问题。

例2:如图6所示,A、B为等量异种点电荷,O是AB连线的中点,D为AB连线中垂线上某一点,试比较C、D两点场强的大小。

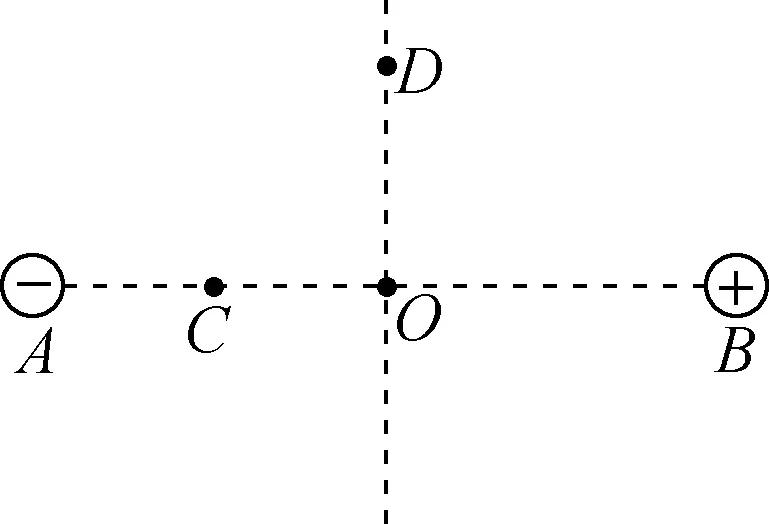
图6

分析：要比较C、D两点的场强大小,通常是将C、D两点处场强的表达式写出来，然后比较大小。在实际教学中很多同学就是想从这个角度去解决,但由于C、D具体位置未知,故此路不通。有的学生想到利用电场线的疏密程度来进行比较,故画出A、B间电场线如图7所示,由图7发现：C、D处电场线的疏密情况不明确,由于画图的差异,有部分学生甚至会得出相反的结论。至此,不少学生觉得陷入了“绝境”。此时教师提问：能否比较C、O处场强大小呢？学生几乎异口同声回答：EC>EO,理由是C处电场线比O处密。接着再提问：能否比较D、O处场强大小呢？学生回答：EO>ED(关于等量异种电荷连线中垂线上各点场强关系在前面已做了专门讨论),即可得到：EC>ED。这时教师又提出一个问题：C、D两点电势的高低如何？受前面的启发,很多学生很快得出φC<φD=0。

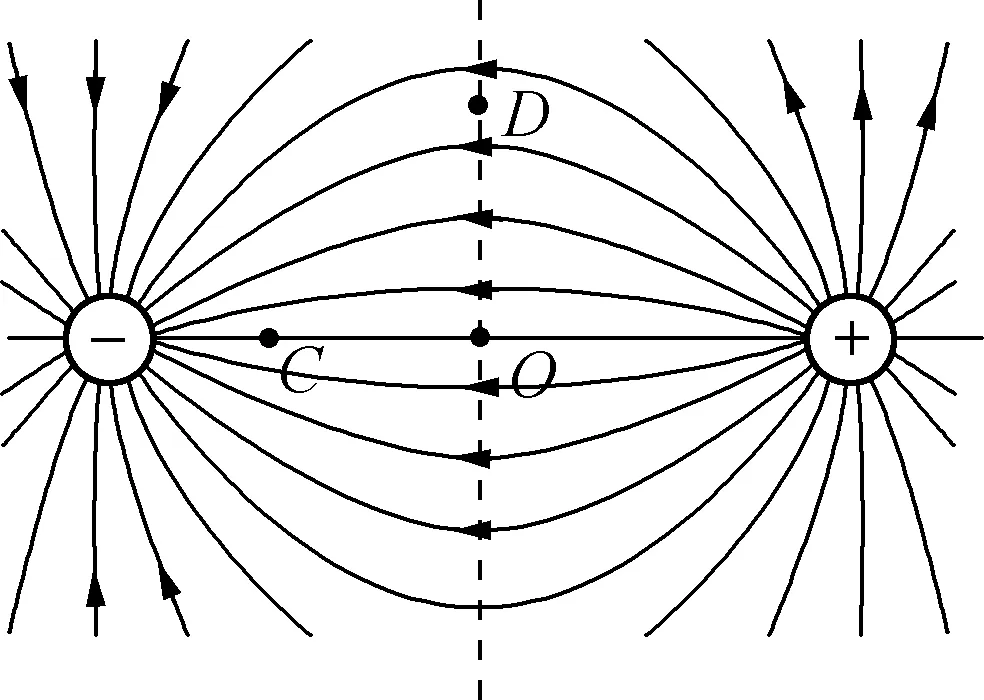
图7

C、D两点场强的大小看似无法比较,但经老师的点拨,架起了“O”点这个桥梁,问题很快得以解决。学生是学习的主体,教师不能越俎代庖,应该起引导、启发、点拨的作用。让学生在老师的启发下,能自主架起解决问题的“桥梁”,进而解决问题。

有的问题比较难,搭建一个“桥梁”还不够,就需要搭建多个“桥梁”。搭建“桥梁”也是一种艺术,什么时候搭？搭什么样的“桥梁”？这就给教师提出了很高的要求。教师本身必须对所教学科有精深的理解,同时又要了解学生的认知特点、知识基础等,才能在遇到不同的问题时能给学生搭起合适的“桥梁”,达到引导学生思考、启迪学生思维的目的。

4 架设师生情感“桥梁”，使学生“爱屋及乌”

心理学研究表明：学生认知水平的高低,与学生在认知活动中是否形成良好的情感体验有重要的关系。美国哈佛大学的戈尔曼认为：情感比智力更重要,教育的作用不仅要让学生形成认知效应,更要通过其产生心理效应,两种效应相辅相成。

教学是师生的双边活动,师生间存在着知识和情感交流,两种交流相互影响,当知识和情感交流都顺畅时,总流量最大。良好的师生情感交流有助于教师洞察学生的心理世界，因此教师要热爱、亲近学生,理解、尊重、信任他们,关心他们的学习和生活,尽力及时解决他们各方面存在的困难,使他们体会到老师对他们的真诚之爱，从而形成一种融洽的、和谐的、亦师亦友的关系。另外，教师的情绪极易感染学生,当教师面带微笑,怀着愉悦的心情走进教室时,学生会倍感亲切,快乐之情油然而生。学生思维活跃,师生配合默契,这样才有利于知识信息的传递。学生从喜欢物理老师开始,到喜欢上物理课,最终会喜欢物理这门学科。正如古人所说：“亲其师而信其道”。使学生的良好情绪逐渐上升为爱物理的情感。学生学习的积极性大大提高,物理学习的进步当然会顺理成章。

通过搭建“桥梁”使学生学好物理,“桥梁”有很多,但最大的“桥梁”一定是教师。孟子曰：“资之深,则取之左右逢其源”。教师作为“传道授业解惑”者,务必提高自身的教育、教学能力。教育是一门艺术,“教学有法,教无定法”,教师既要掌握教育教学理论,又要掌握教学的艺术；既要学习借鉴名师的经验,又要养成自身独特的风格。因此,教师要不断追求更好的教学设计、更优的教育方法,使日复一日、年复一年的教育教学工作呈现新的效果、达到新的境界，真正做一个有理想信念、有道德情操、有扎实学识、有仁爱之心的“四有”教师。