水火电机组调速器死区对超低频振荡的影响分析

范成围

(国网四川省电力公司电力科学研究院，四川 成都 610041)

0 引 言

随着渝鄂背靠背工程的投运，西南电网与西北、华中、华东3个区域电网异步互联，使得四川的电源结构性矛盾更为突出[1]。四川电网水电装机总量大、占比高，水电机组调节性能、动态特性的好坏严重影响电网的稳定性。系统转动惯量显著减小，系统频率波动将明显加剧，这对系统频率调节策略提出了更高要求。

近年来，异步联网系统振荡现象逐步显现，国内外电网发生了多起超低频率振荡事件[2]。现有研究发现，水轮机是造成超低频振荡发生的主要原因[3-5]。调速器成为控制水轮机动作特性的关键元件，优化参数设置是解决超低频振荡问题的有效手段。

系统频率稳定与调速器一次调频性能密切相关[6]，为提升高水电占比电网在超低频段的阻尼水平，需要减小调速器PID参数[7]；然而，过小的调速器参数将显著降低一次调频性能，不利于大扰动后频率恢复，系统高频和低频风险突出[8]。故调速器PID参数需要在一次调频性能和超低频振荡抑制两个矛盾的目标中平衡。

除了控制参数以外，调速器的死区对系统的调频能力影响不可忽略。死区既是调速系统机械环节中不可避免的环节，同时也是避免调速器频繁动作的主要手段。如果能够合理设置死区，则可以实现抑制超低频振荡的目的，同时也能维持系统调节频率超限的能力。因此，下面针对四川电网水电占比高的特性，分析水、火电机组的调速器死区对超低频振荡的影响。

1 超低频振荡机理分析

由于水的惯性，导致在水轮机导叶开度变化时，流量不会立即变化。在水轮机导叶变化初期，有功功率初始冲击与导叶位置变化的方向相反：开启导叶时，因压力降低导致功率下降；关闭导叶时，因压力增加导致功率上升。水轮机功率最终按水锤时间常数Tw逼近导叶控制指令，如式(1)所示。

ΔPm(t)=[1-3e-(2/Tw)t]ΔG

(1)

式中:ΔPm为水轮机机械功率;ΔG为导叶控制指令对应的功率。

水轮机的上述特性导致其成为“非最小相位系统”，在系统解列或水电机组孤立运行期间，可能因水轮机控制不稳定导致超低频振荡现象。

调速器和原动机组成的系统如图1所示。

图1 调速器、水轮机联接模型

典型水轮机调速系统总体简化模型可表示为

(2)

式中:ΔTm为水轮机调速系统输出机械转矩;ΔPE为电磁功率;Δω为频率偏差量;KP、KI为PID控制器中比例系数和积分系数;TR为调速器控制时间常数;T为水轮机伺服系统时间常数。

对特定的振荡频率，有

ΔTm=GGOV(jωd)K(-Δω)=-α∠β·Δω

(3)

式(3)将机械转矩ΔTm表示为调速系统传递函数GGOV(jωd)K和频率偏差Δω的乘积，用α简化表示。调速系统产生的移相角β随频率的变化而变化。针对超低频振荡的频率区间，移相角β运行在负阻尼区间。水电调速系统在低频段具有明显的相位滞后效应，典型参数下水电机组调速系统在低频段范围内均提供负阻尼。

2 四川电网典型调速器系统

调速器和原动机系统的传递函数为

G=G调速G水、汽轮机

(4)

ΔPm=DGΔω+KGΔδ

(5)

式中：ΔPm为原动机机械功率变化；Δw为转速偏差；Δδ为功角变化；DG为阻尼转矩系数；KG为同步转矩系数。

由ΔPm与Δω之间的传递函数可知，DG>0时发电机将向系统提供正阻尼。分析水轮机调速系统及原动机开环传递函数的阻尼特性，将调速系统提供的转矩在ω轴上的投影(即调速系统提供的阻尼转矩分量)定义为调速系统的阻尼系数，借此评估调速系统的阻尼性能。

四川电网主要包括水电和火电两种能源。在PSASP数据模型中，火电机组调速器模型主要为4型，水电机组调速器模型主要为7型，且仅有开度模式。所有传递函数的参数都展示于模型框图中，详细信息参考PSASP用户手册[9]。

1) 4型汽轮机调速器模型

4型调速器由电液调节系统、电液伺服机构、汽轮机模型、主汽压力变化模型组成。

图2为忽略功率信号、只考虑转速信号时的电液调节系统。该系统采用负荷反馈控制，频率偏差Δω到阀门开度PCV的传递函数可表示为

(6)

图2 电液调节系统

图3为以PCV为输入、PGV为输出的电液伺服机构，其传递函数为

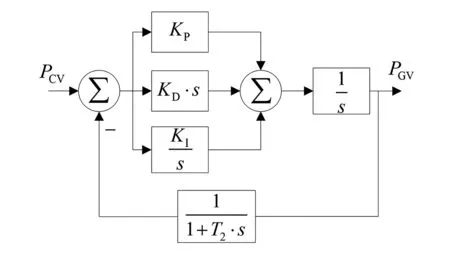
图3 电液伺服机构模型

(7)

图4为汽轮机模型框图，其传递函数为

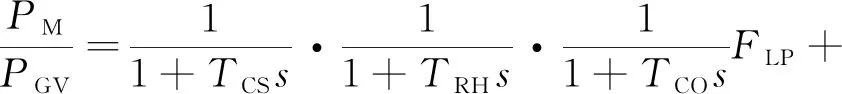
(8)

图4 汽轮机模型

2) 7型水轮机调速器模型

7型调速器包含调节系统、液压系统以及水轮机模型。附加调节方式为开度模式，调节系统的模型框图如图5所示。

图5 调节系统

调节系统传递函数为

(9)

液压系统的模型框图如图6所示，其传递函数为

(10)

图7为考虑水锤效应的水轮机模型，其传递函数为

(11)

图6 液压系统(含执行机构)模型

图7 水轮机模型

以上两种调速系统是四川电网中的典型调速模型，下面将其作为重点，研究对应的死区配置对超低频振荡的影响。

3 算例分析

3.1 仿真模型

忽略网络和负荷特性，利用频率响应模型研究多机电力系统的超低频振荡问题是较为常用的方法[10-11]。针对四川电网的水、火电混合系统特性，在Simulink平台上建立如图8所示的单机带两台调速器的频率响应模型，以研究不同能源机组的死区如何影响超低频振荡。

图8 单机两调速器系统

忽略系统网损，考虑负荷频率调节效应和发电机阻尼系统后，图8中等值发电机的传递函数为

(12)

式中：TJ为发动机的转动惯量；Ds为发电机阻尼系数与负荷频率调节效应系数之和。

7型水轮机调节系统采用PI控制。忽略伺服系统微分和积分环节，结合典型仿真数据，调速系统传递函数可以简化为

(13)

对于实际电网仿真，4型汽轮机通常考虑高压蒸汽和中间再热蒸汽容积效应，调速器保留调差特性，伺服系统忽略微分和积分控制，结合四川电网典型仿真数据，调速系统传递函数可以简化为

(14)

仿真参数设置如下：

1)发电机Ggen参数为TJ=10.0s，DS=0.4；

2)水轮机Ght及其调速器Ghgov参数为KP=0.5，KD=0.7，KI=1，TW=1，TGH=0.2，bP=0.04；

3)汽轮机Gst及其调速器Gsgov参数为R=0.030 3，TG=0.2，FHP=1，TRH=10，TCH=12。

另外，设置b1和b2分别为水轮机调速器和汽轮机调速器的死区，通过改变死区的大小，测试在不同的扰动输入下，死区对频率振荡的影响。

3.2 死区大小影响分析

所建立的系统由1台火电机组和1台水电机组构成，分别以不同的死区配置进行仿真，将扰动由小到大按步长0.000 1增加，直到系统首次出现发散的振荡波形，记录此时的扰动大小，以此作为该死区配置下的临界扰动大小。当扰动大于临界扰动时，系统不稳定；当扰动小于临界扰动时，系统稳定。算例中水、火电机组调速器死区分别为0.007 pu和0.005 pu时(基于50 Hz)，以不同幅值的扰动大小测试系统，发现当扰动幅值在0.020 0时，激发出收敛的波形，系统是稳定的；而当幅值增加到0.020 1时，波形发散，系统失稳。如图9所示。所以0.020 1即是该死区配置下的系统临界扰动值。用同样的方法测试不同死区配置的仿真，结果如表1所示。

图9 频率分析的系统等值模型

以算例1作为基准，将其他算例的结果与之进行比较，分析讨论死区对系统稳定性高低的影响。

表1 不同死区的临界振幅值

1)水、火电机组死区独立影响

以算例1为基准，将算例2(单独增加水电死区)和算例3(单独增加火电死区)的结果与之比较，可以看出：两者死区的增加都增加了临界扰动的大小；并且临界扰动对水电机组调速器的死区更为敏感，同样增加0.001 pu的死区大小，算例2的临界扰动增幅更大。

2)共同改变死区

将水、火电机组调速器死区同时增加(算例4)或同时减少(算例5)，临界扰动的幅值也随之增大或减小。临界扰动幅值与死区大小的变化正相关。

3)相互反向改变死区

将水、火电机组调速器相互以相反方向改变死区大小，其中算例6中水电死区减少、火电死区增加，其临界扰动比算例1减小；而算例7中水电死区增加、火电死区减少，其临界扰动比算例1更高。相比算例1，算例6和算例7中水、火电机组调速器死区值的改变量绝对值相同。结果证明，增加水电死区、减少水电机组的调频参与度，同时减少火电机组死区、增加火电机组的调频参与度，对系统的频率振荡有较好的抑制作用，同时也保持了系统的频率调节能力。

4 结 语

调速器死区对超低频振荡的抑制作用比较明显，死区越高则系统发生超低频振荡的风险越低。但不同能源机组的调速器死区对于超低频振荡的抑制效果不同。通过调节水电机组的调速器死区能够明显改变使系统发生频率振荡的扰动幅值，而火电机组则效果较弱。综合来看，不论单独提高某种机组还是共同提高水、火电机组死区，都可以达到抑制超低频振荡的目的，但相应却可能减少系统的调频能力；由于水、火电机组对超低频振荡的影响存在差异，可以通过提高水电机组死区、降低火电机组死区的方法，达到抑制振荡和保持调频能力的平衡。合理配置调速器死区，实现不同调频手段的优化控制，是利用死区设置抑制超低频振荡的有效手段。