基于VMD 时频分析方法的颤振试飞应用研究

王绍楠，刘立坤

（中国飞行试验研究院，西安 710089）

颤振试飞信号具有信噪比低、模态密集、非平稳的特点，且随着飞机设计中折叠机翼的出现，复合材料的大量使用以及飞机外挂复杂化，使得信号的非平稳特征更加突出[1]。对非平稳信号处理成为飞行试验工程中不可回避的问题[2]。

传统的信号处理最常采用的方法是傅里叶变换（FFT），但该方法不适用于瞬态信号和非平稳信号，只是一种单纯的频域分析方法，无法获取时域信息。短时傅里叶变换和小波变换虽然能改进不足，能满足信号的时频局部化分析，但其本质还是属于傅里叶变换。小波分析结果受小波基影响很大，目前缺乏系统规范的小波基选取方法，且小波变换是非自适应的，小波基一旦被选定，整个分析过程只能采用同一小波基。1998 年，美籍华人N. E. Huang[3]提出了一种针对非平稳、非线性的数据处理方法，称为希尔伯特黄变换（Hilbert-Huang Transform，HHT）。该方法以经验模态分解（Empirical Mode Decomposition，EMD）为核心，能够自适应地将非平稳信号分解为单一组分的平稳信号，在处理非平稳信号方面有着广泛应用。但该方法实践超前于理论，目前尚没有严格的理论支持。2005 年，Smith 等[4]提出了局部均值分解（LMD），但递归式的模态分解（EMD、LMD 等）采用的是基于极值点的包络求取方法，多次的递归式分解会很大程度上增加计算误差，容易出现模态混叠。虽然采用集成式模态分解方法，如EEMD[5]和ELMD[6]，可在一定程度上抑制模态混叠现象，但计算量将大幅增加，且这两种方法也无法将两个频率相近的分量正确分离，均存在采样效应和端点效应的问题。

直到2014 年，Dragomiretskiy 等人[7]提出了一种完全不同于递归式模态分解的新方法，称为变分模态分解（VMD）。该方法理论的总体思路为求解变分问题，具有坚实的理论基础。其假设信号是由若干个不同的具有中心频率和有限带宽的模态组成，由此构造变分问题。再通过乘法算子交替方向法不断搜寻变分问题最优解，使得每个模态的估计带宽之和最小。最终，自适应地将信号中的单一组分模态成功分离。VMD 可以将两个频率接近的谐波信号很好分离，表现出更好的噪声鲁棒性。相比于递归式的模态分解方法，VMD 的端点效应也更弱[8-9]。

VMD 一经提出，即成为众多研究者研究的热点[10-13]。目前，该方法已用于机械、电子、生物、能源等领域，尤其在机械故障诊断中应用最广[14-20]。武英杰等[11]将VMD 应用于风机电组故障诊断中，证明了VMD 比EMD 和LMD 等递归式模态分解方法，能更有效地避免噪声和冲击信号的频率混叠现象，也更适合提取信号中的低频成分。赵岩等[14]将VMD 用于旋转机械碰摩故障诊断，并得出该方法与EEMD相比可以有效抑制模态混叠，更加准确地反映故障信息。唐贵基等[15]将参数优化变分模态分解方法应用于滚动轴承的早期故障诊断。陈立军等[17]将VMD 应用于水声跳频信号的时频分析，结果表明其能在低信噪比情况下获得高清时频图。刘长福等[18]将VMD 用于变切深侧铣颤振特征的提取。然而，还未有将该方法应用于颤振飞行数据处理的研究报道。鉴于该方法在处理信噪比低、模态密集、非平稳信号中的优势，文中首次将VMD 方法引入颤振试飞领域，将其与希尔伯特变换结合，用于颤振试飞数据的时频分析。

1 理论介绍

1.1 变分模态分解（VMD）理论

在VMD 算法中，本征模函数（IMF）被重新定义为一个调幅-调频信号，表达式为：

为求以上变分问题的最优解，引入了二次罚因子α 及拉格朗日乘法算子 λ(t) ，得到如下的扩展拉格朗日表达式：

1.2 基于VMD 的时频分析方法理论

通过1.1 节介绍的VMD 将初始信号分解为不同的IMF 分量进行希尔伯特变换得：

Re 表示取实部，式（7）右端即为希尔伯特谱。它表示瞬时振幅在频率-时间平面上的分布，记作：

2 仿真算例

为验证该时频分析方法的正确性，构造仿真信号f，由三部分组成，如式（9）所示：

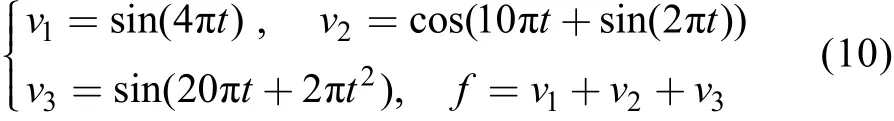
式中：v1是频率为2 Hz 的正弦信号；v2是余弦调频信号，频率随时间成正弦波动，其频率值以5 Hz为中心，在4～6 Hz 之间成余弦波动；v3为正弦扫频信号，频率从10 Hz 起，呈2 Hz/s 线性增加。构造的仿真信号时间为6 s，仿真信号f的时域波形如图1所示。

图1 仿真信号f 的时域波形Fig.1 Waveform of simulation signal f in time domain

采用VMD 对原信号进行分解，模态数K取5。VMD 分解信号的频谱与仿真信号的对比如图2 所示，其中黑色虚线为仿真信号频谱。从频谱中能清晰看到该信号第一个组分的主频为2 Hz，第二个组分信号5 Hz 及其变化边界4 Hz 和6 Hz，还有第三个组分信号从10 Hz 变化到22 Hz 的谱图。此外，还有信号中没出现过的3 Hz 和7 Hz 的 “伪” 谐波分量。

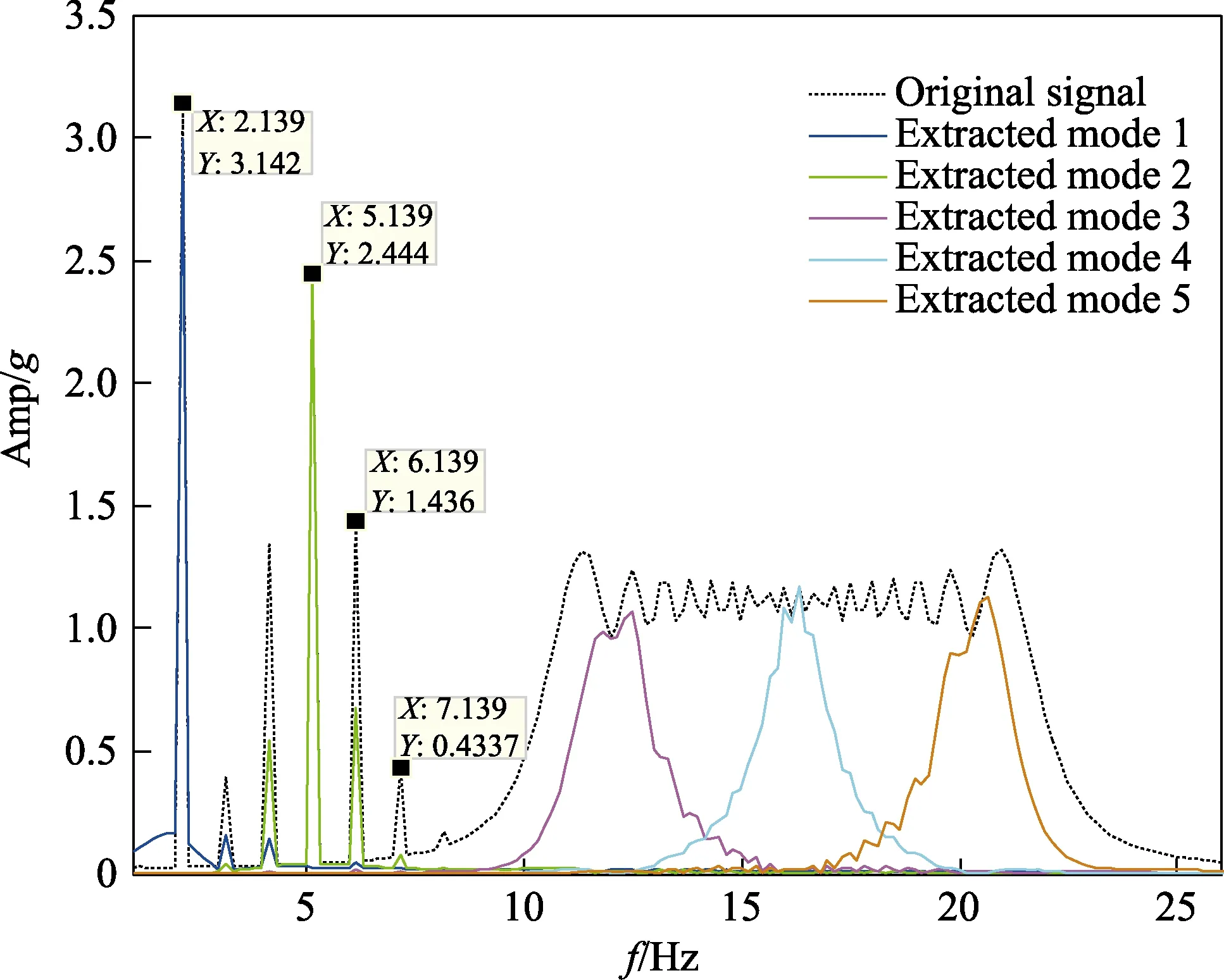
图2 VMD 分解频谱与仿真信号对比Fig.2 Comparison between the frequency spectrum decomposed by VMD and the simulation signal

由于设置模态数为5，故VMD 分解出了u1～u5共5 个谐波分量，结果如图3 所示。图3 第一行为原始信号波形，之后从上到下依次为VMD 分解得到的谐波分量与原始信号分量的对比。其中，虚线显示的是原信号分量的波形，实线为VMD 分解的波形。可见，VMD 准确地分解出了前两个组分信号，对应了原信号中的v1和v2。v3是频率变化很快的扫频信号，VMD 分了3 次对该信号进行了分解。u3、u4和u5分别对应了该信号的不同频率段的波形，但都与v3对应段的波形吻合良好。

图3 VMD 分解结果与仿真信号对比Fig.3 Comparison between the result decomposed by VMD and the simulation signal

图4 基于VMD 的时频分析图Fig.4 Time-frequency analysis diagram based on VMD

VMD 方法的时频分析如图4 所示，描绘了信号不同组分的频率随时间的变化。为了对比，采用小波分析的方法也对这段信号进行了时频分析，分辨率取0.2 Hz，如图5 所示。可见，基于VMD 的时频分析方法可以很好地展示出原非平稳信号的时频特征，包括频率随时间线性增长和正弦波动的特性，而小波分析无法描绘出频率呈正弦变化的过程，得到的频带也不够清晰。

3 试飞应用

某型飞机在某高度跨音速飞行时，给外挂物上施加侧脉冲激励，外挂物的振动响应并未衰减，而是出现等幅振荡的异常现象。施加激励后外挂物的时域振动如图6 所示。

图5 小波分析时频图Fig.5 Time-frequency diagram of wavelet analysis

图6 外挂物的振动时间历程Fig.6 Vibration time history of the aircraft stores

将时域信号放大，可见在整个振荡过程信号波形有变化。为研究其非平稳的变化特性，采用VMD 时频分析方法对典型的不同特性的三段信号进行分析。第一段为0～3 s（如图7 所示），可见，VMD 方法完全捕捉到了所有的频率成分。从时域波形看出，在0.3 s 时施加的激励，从时频图中可见，在施加激励前9 Hz 频率就存在，对应了外挂物的侧平振动。施加激励后，其振幅逐渐衰减，而17.5 Hz 的振动是在施加激励后才被激发出来，对应了外挂物的偏航振动，伴随出现的还有它的2 倍频。第二段为7.8～10.3 s 数据（如图8 所示），可见9 Hz 模态已消失，只有17.5 Hz模态及2 倍频存在。第三段为18～21.3 s 数据（如图9 所示），该段信号时域幅值略有增大，且波形有明显变化，波峰与波谷出现许多锯齿，类似多频率的叠加现象。从频谱图和时频谱图可见，该段只呈现外挂物偏航振动，同时出现了其2 倍频和3 倍频，且偏航振动频率由最初的17.5 Hz 左右变为了16 Hz 左右。即脉冲激励后，主要呈现的是外挂物的持续偏航振动，随着时间的推移，其倍频振动也越发显著，振幅在后期还有增大趋势，直到飞机减速爬升，退出异常振动过程，该振动才衰减。由此，通过基于VMD 的时频分析可以清楚详细地分析出外挂物以偏航振动为主导的极限环振荡过程，找到了故障的来源，为解决异常振动问题提供支撑。

图7 前0～3 s 信号分析结果Fig.7 Analysis results of the first 0～3 s: a) time domain signal of interception section; b) comparison between signal spectrum decomposed by VMD and intercepted spectrum; c) time frequency analysis based on VMD

图8 前7.8～10.3 s 信号分析结果Fig.8 Analysis results of the first 7.8～10.3 s: a) time domain signal of interception section; b) comparison between signal spectrum decomposed by VMD and intercepted spectrum; c) time frequency analysis based on VMD

图9 前18～21 s 信号分析结果Fig.9 Analysis results of the first 18～21 s: a) time domain signal of interception section; b) comparison between signal spectrum decomposed by VMD and intercepted spectrum; c) time frequency analysis based on VMD

4 结论

1）基于VMD 的时频分析方法能细致清晰地展示出非平稳信号的时频特性，有较高聚集度。

2）该方法在实际颤振试飞数据处理应用中取得了良好效果。对于飞行异常振动数据，有助于分析试飞故障来源，为后续问题解决提供支撑。