基于应变模态方法的飞机蒙皮分布动载荷识别

张丛，付益战，李元栋，李家旭

（中航飞机股份有限公司汉中飞机分公司，陕西 汉中 723213）

当今运输类飞机的发展，随着轻质化、高推重比等需求，对于飞机结构设计提出了更高的要求。在飞机结构设计中，结构载荷输入是设计人员必须考虑的关键因素，它对于飞机结构设计优化具有十分重要的意义。运输机在飞行过程中，机身蒙皮在流场中受到分布动态载荷的作用。机身蒙皮在动态载荷的作用下引发结构振动和噪声，影响机上人员的舒适性，过度振动甚至可能导致飞机结构疲劳破坏，进而影响飞行安全。然而，由于环境工况的影响，在飞机蒙皮外侧布置压力传感器十分困难，机身蒙皮所受分布载荷通常很难在飞行过程中进行直接测量。因此，如何确定飞机在飞行过程中受到的分布动态载荷成为飞机结构设计人员亟待解决的一大难题。

结构系统的动态载荷识别技术，作为结构动力学研究的第二类逆问题[1]，是在已知结构系统的动力学特性的条件下，通过测量结构系统的动态响应来反推载荷输入的过程，为动态载荷确定方法提供了新的思路。载荷识别技术的研究从20 世纪70 年代开始[2]，经过近几十年的不断发展与完善，目前已经成为解决复杂工程问题载荷预估的重要手段。文献[3]提出了基于广义正交多项式的复杂分布动载荷识别技术，该方法采用切比雪夫正交多项式为基函数，通过获取有限个测点的位移响应识别基函数系数，从而得到以基函数叠加形式的分布载荷函数。该方法识别精度较高，具有很好的工程应用价值，但由于在结构共振频率附近位移频响函数矩阵的奇异性[4-5]，此种方法的识别精度受位移响应测量的准确度影响较大。

1988 年，李徳葆、夏苏等[6]采用逻辑演绎的方法推导了结构应变频响函数矩阵。1989—1996 年，李德葆、罗京等[7-9]采用直接微分法和有限元方法对应变模态理论进行了推导和论证，并采用计算仿真和实测实验对应变模态理论进行了对比验证。随着应变模态理论的不断发展，其理论研究已趋于完善，应变模态方法被广泛应用于机械设备的故障诊断和结构损伤识别等领域，也有少部分用于动态载荷识别。

文中结合复杂结构分布动载荷识别的正交多项式拟合法和应变模态理论，建立了基于应变模态方法的飞机蒙皮分布动载荷识别模型。采用软件仿真的方法，对某型飞机蒙皮分布动态载荷进行了识别，并对载荷识别的数值稳定性进行了分析研究。

1 基本理论

1.1 蒙皮分布载荷识别模型的建立

对于受分布载荷F(x，y，ω)作用的矩形区域，其任一测点i的应变响应Wiε(ω)为：

对于L个测点的应变响应值为：

将F(x,y)写成已知基函数T(x,y)叠加的形式：

可得：

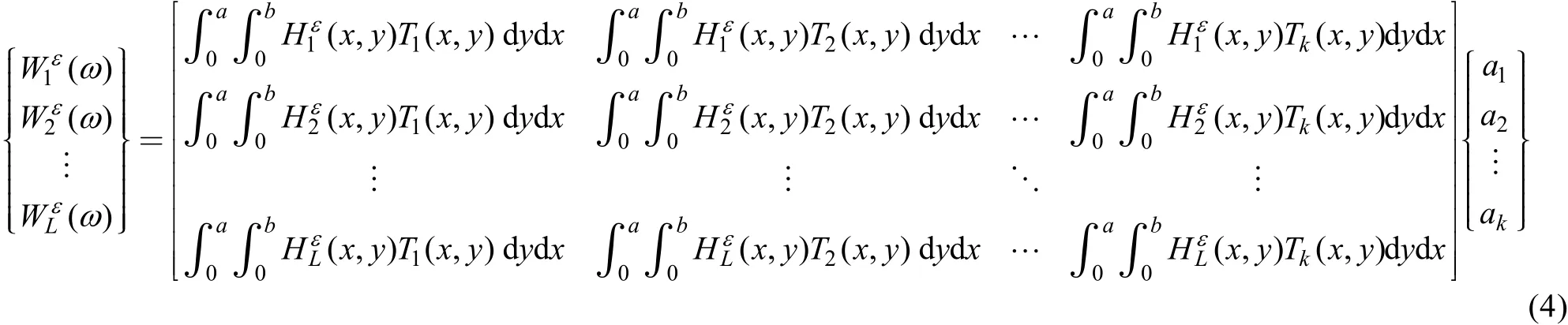
写成矩阵形式：

式中：为每个测点应变响应组成的矢量，可由应变传感器直接测得；T为应变传递函数和正交基函数乘积的积分组成的矩阵，简称应变积分矩阵；a为待识别的系数组成的矢量。T中应变频响函数可通过模态试验或仿真分析得到，其理论推导过程详见文献[10]。基函数为已知函数，因此系数向量a是可识别的。

积分矩阵T为L×k阶矩阵，当L=k时，T为方阵，系数向量可直接求逆得到：

1.2 基函数的选取

文献[11]提出采用切比雪夫广义正交多项式为基函数，具有较好的拟合效果。在文中的载荷识别过程中，也选用正交多项式作为插值基函数，具体为：

2 有限元仿真计算

2.1 模型简介

以某型飞机机身中段壁板为例，利用Patran 软件建立机身中段壁板有限元模型。模型以壁板一角点为坐标原点，顺航向为x轴，垂直向上为y轴，长l=2 m，高h=1.2 m，曲率半径 为2 m，蒙皮厚度2 mm，壁板四周简支约束，在壁板蒙皮内侧选取16 个响应测点。壁板有限元模型及测点布置如图1 所示。

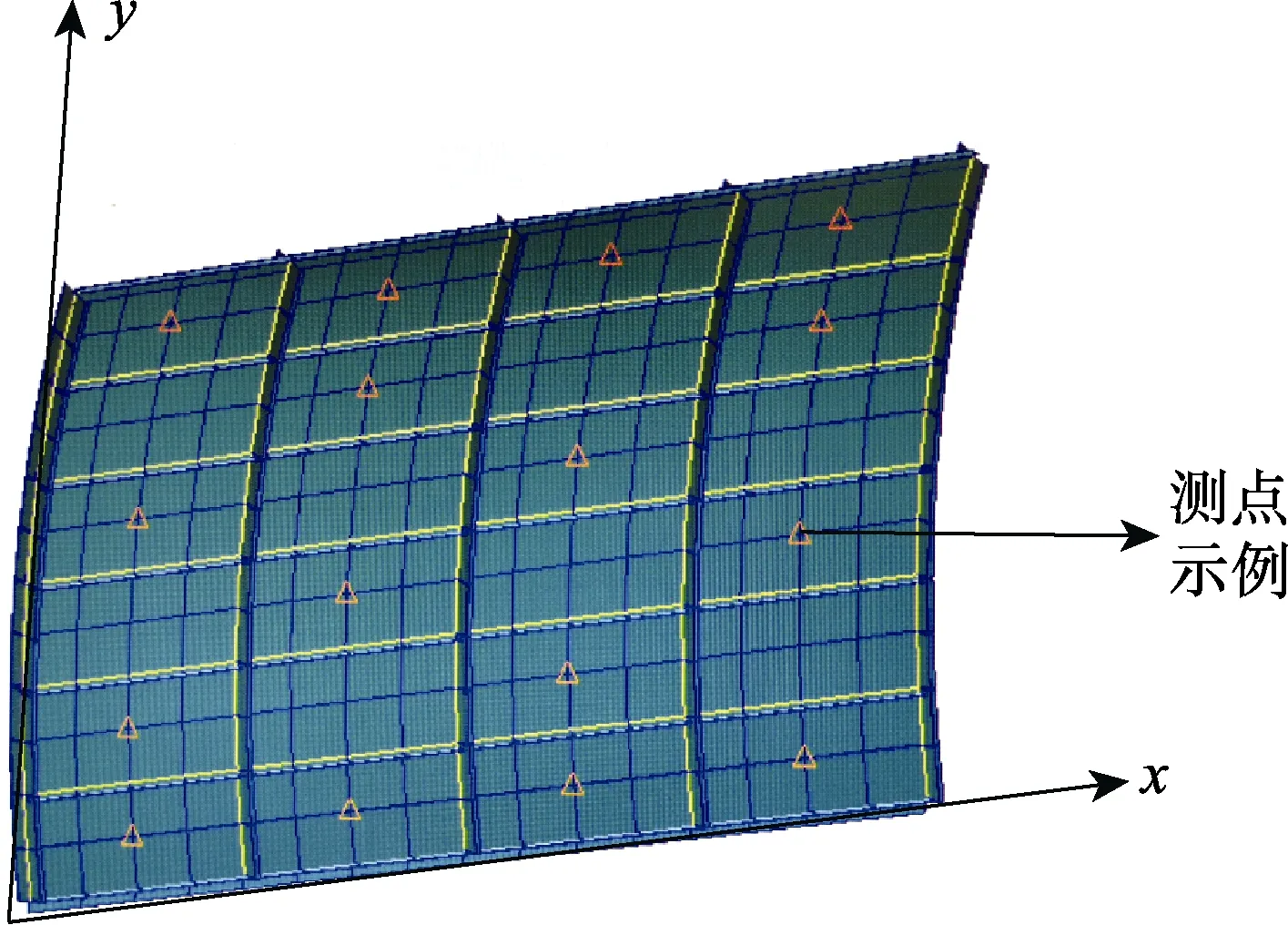
图1 某型机外侧壁有限元模型及测点布置Fig.1 FEM model and measuring point layout of aircraft skin

2.2 载荷识别

在计算模型蒙皮外侧，施加幅值为P(x,y)=1000-200(x-1)2-300(y-0.6)2，相位为0°的简谐分布载荷，如图2 所示。以有限元软件Nastran 计算的频率响应结果作为测点的响应，取3×3 阶正交多项式，分别用应变和位移方法识别其70、80、90、100 Hz 下的载荷幅值，识别多项式系数见表1、表2，各频率下的识别误差见表3。由表3 可知，采用应变模态方法的某型飞机蒙皮分布载荷识别最大误差为8.9%，采用位移方法的载荷识别最大误差为8.14%，二者识别误差均小于10%，且最大误差均发生在蒙皮边界附近，满足工程应用要求。识别分布载荷及误差（仅以70 Hz为例）如图3、图4 所示。

表1 应变载荷识别多项式系数Tab.1 Polynomial coefficients of strain load identification method

表2 位移载荷识别多项式系数Tab.2 Polynomial coefficients of displacement load identification method

表3 各频率下载荷识别最大误差Tab.3 The maximum error of load identification at each frequency

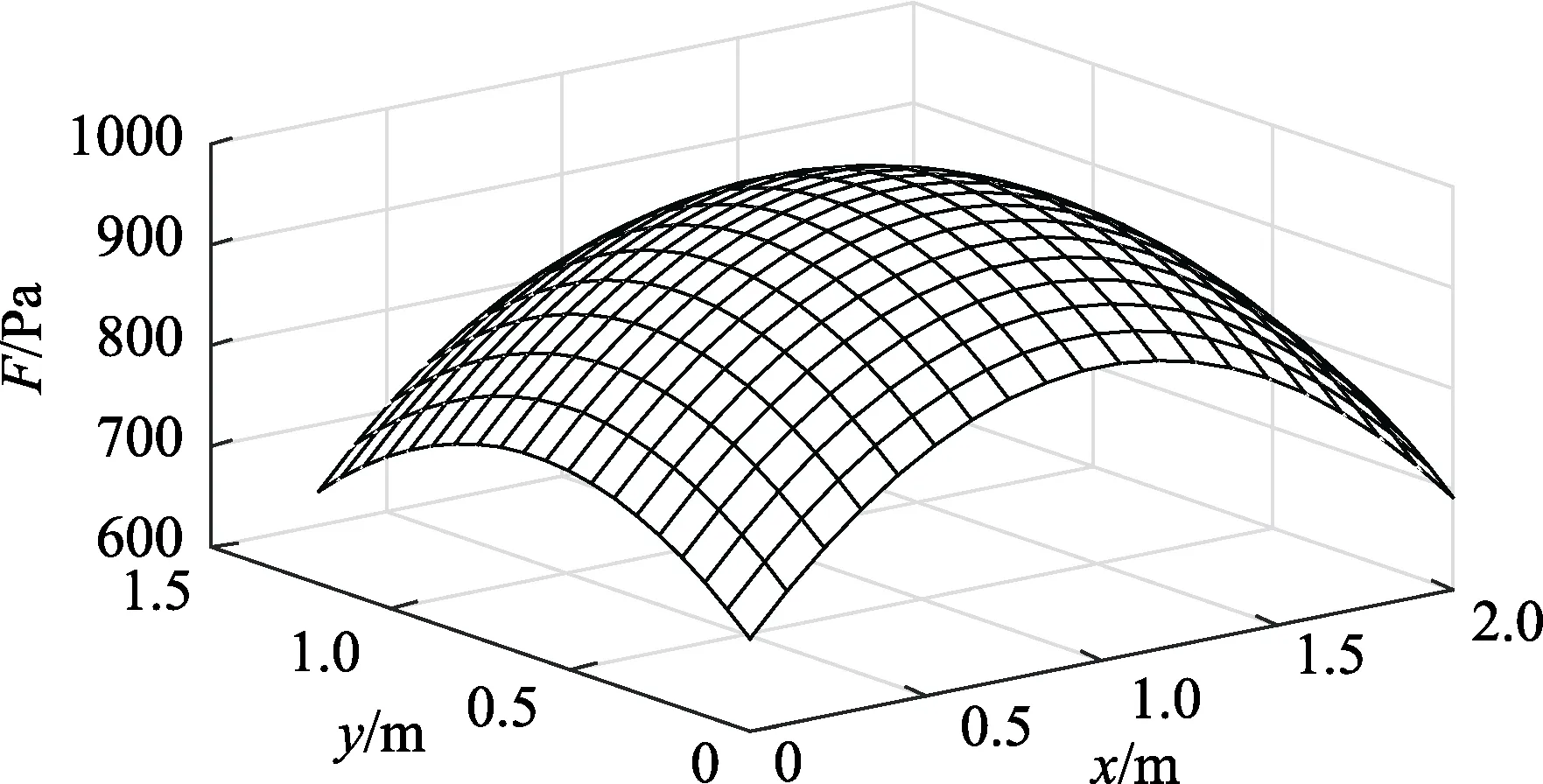
图2 实际施加分布载荷Fig.2 Actual applied distributed load

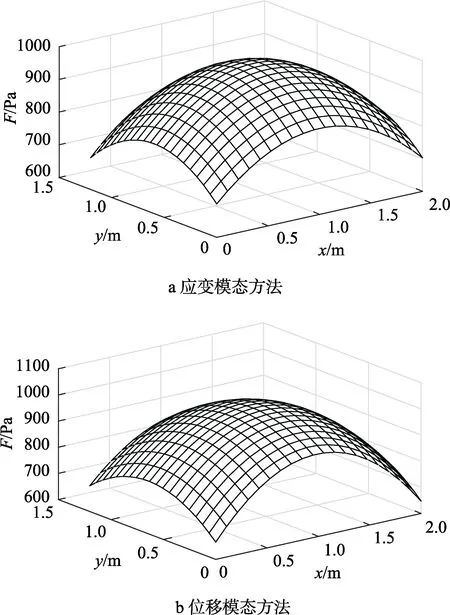
图3 70 Hz 载荷识别结果Fig.3 Load identification results at 70 Hz:a) strain mode method; b) displacement mode method

3 数值稳定性分析

根据应变模态理论，结构应变频响函数可通过位移频响函数的微分运算进行推导，结构应变响应与位移响应之间也存在微分运算关系。因此在上述应变模态方法载荷识别过程中，式（5）为采用位移模态方法的微分函数方程组。微分运算后，矩阵T的条件数发生变化，从而影响载荷识别的数值稳定性。为分析载荷识别的数值稳定性，分别求式（7）中采用应变模态方法和位移模态方法的积分矩阵（TTT）的二范数条件数，计算结果见表4。

图4 70 Hz 载荷识别误差Fig.4 Load identification error at 70 Hz:a) strain mode method; b) displacement mode method

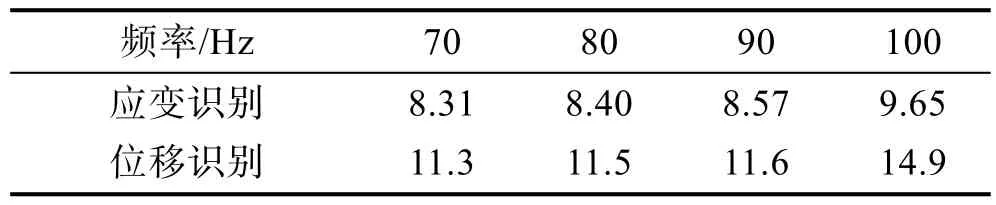
表4 各频率下载荷识别积分矩阵条件数（105）Tab.4 The condition number of integral matrix at each frequency (105)

由表4 可知，各频率下，利用应变模态方法进行载荷识别的积分矩阵条件数小于位移方法，表明采用应变模态方法的载荷识别数值稳定性好于位移模态方法。为验证应变模态方法和位移模态方法载荷识别的数值稳定性差异，将仿真算例中100 Hz 下的应变响应数据和位移响应数据增加3%的随机干扰，进行载荷识别。应变模态方法和位移模态方法载荷识别的最大相对误差分别为9.8%、19.4%。由计算结果可知，加入随机干扰后，采用位移方法的载荷识别误差较大，无法满足工程应用，而采用应变模态方法的载荷识别仍具有较好的识别精度，表明采用应变模态方法的分布载荷识别方法具有更好的抗干扰能力。

4 结论

对基于应变模态方法的动态分布载荷识别理论进行了研究，通过有限元仿真手段，分别采用应变和位移模态方法对某型机蒙皮所受分布动载荷进行了识别。结果表明，基于应变模态方法的飞机蒙皮分布动载荷识别方法具有较好的识别精度，满足工程应用。对各个频率下积分矩阵的条件数的计算表明，采用应变响应进行载荷识别的方法比传统意义上的采用位移响应进行载荷识别的方法具有更好的数值稳定性。同时，飞机蒙皮应变响应数据可通过在机身蒙皮内侧布置应变片进行直接测量，受环境工况的限制较小，具有很好的应用价值。