基于统计复杂度的分数阶欠阻尼双稳系统的随机共振研究

党蒲妮，孙中奎，吕锦锋

（1.航空工业第一飞机设计研究院，西安710089；2.西北工业大学 应用数学系，西安 710072）

在自然界和工程社会中，“噪声” 通常被认为是对系统有害的。直到1981 年，著名的意大利科学家Benzi 等人在探究地球冷暖气象问题时，首次推出 “随机共振” 这一概念[1]，并首次阐述了噪声对于非线性系统的建设性作用。其含义本质上是指噪声的加入，增强了系统的响应强度，主要体现了系统非线性输出中弱周期信号的输入与随机力的协同效应。经典的随机共振理论已被广泛应用于物理学[2]、生物学[3]、化学[4]等各个学科领域，且关于随机共振的研究引起了各个领域科学家们越来越多的关注[5-6]。

近些年来，关于分数阶微分在某些反常且复杂的物理学中的研究引起了学者们的探讨，如粘弹性材料的应力松弛问题[7]、粒子的反常扩散问题[8]等。对于粒子的反常扩散行为，分数阶导数可以良好地刻画其所具有的历史依赖性与全局相关性，且可以建立相应的分数阶Langevin 方程来描述此扩散过程[9-10]，因此分数阶系统的动力学研究具有非常重要的意义。经典的整数阶随机共振已具有相当丰富的研究成果[11-12]，而关于分数阶动力系统的研究才刚刚起步[13-14]，特别是在分数阶随机共振的研究方面，内容比较稀少[15-16]。Soika 等[17]探究了二值噪声和加性Gaussian 白噪声共同驱动下的分数阶线性随机系统，通过Shapiro-Loginov 公式和Fourier 变换等方法求解了输出响应振幅的表达式。Yang J H 等[18]通过非线性响应理论法研究了Gaussian 白噪声驱动下分数阶系统的随机共振效应，得到系统响应振幅的半解析解来度量随机共振现象的发生。Sun Z K 等[19]通过统计复杂度方法研究了白噪声激励下分数阶过阻尼双稳系统的随机共振现象，并运用信噪比指标函数验证了此方法的准确性。

文中基于统计复杂度方法来刻画分数阶欠阻尼双稳系统的随机共振现象。首先，给出了标准Shannon熵、统计复杂度以及Bandt-Pompe 算法的定义。其次，介绍了Gaussian 白噪声驱动下的分数阶双稳系统。最后，运用Bandt-Pompe 算法求出统计复杂度和标准Shannon 熵，进而探讨了不同的参数对分数阶系统随机共振现象的影响。

1 信息论测度

统计复杂度作为一种经典的信息论测度，它主要以信息论为基础，用于刻画系统时间序列相对应概率分布的函数，可以度量系统的随机性及其相关结构的存在性。

1.1 标准Shannon 熵

为了更好地定义统计复杂度，首先引入熵的定义，它是表示由概率分布所描述的物理过程的不确定度，定义为：

当 S [ P] = 0时，Shannon 熵最小，表示系统为有序状态，即系统所获得信息量最大。当 S [P] = ln N时，Shannon 熵最大，表示系统为无序状态，且系统所获信息量最小。

进一步，标准Shannon 熵的定义为：

1.2 统计复杂度

此外，为了更好地度量系统的内部结构，笔者给出了失衡度Q [P] ，它是用来测量系统可以达到的状态的概率分布P 和所对应的均匀分布Pe之间的距离长度Ds，其表达式为：

其中 0Q 为归一化常数。度量这两个分布之间的距离Ds，一般采取Jensen 散度，定义为：综上所述，可给出统计复杂度的定义，即 ：

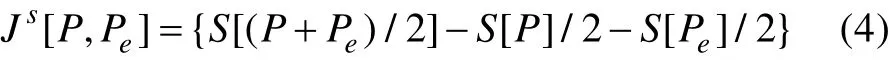
在这里，选取Q [H]为标准Shannon 熵，Q [P] 中的 Ds为Jensen 散度。

1.3 Bandt-Pomp 算法

该方法主要考虑了系统时间序列的时间因果关系，其主要思想是基于吸引子重构的过程所提出。对于给定的时间序列{ xt: t = 1, … , M}和一嵌入维数D ＞ 1，对任意时刻t，分别在时刻选取其相对应连续的D 个数据：，然后重新把这D 个元素进行排序，从而获得对应于序数D 的有顺序的模式为：

式中符号# 表示相对应的数量，且文献[20]中的嵌入维数D的范围为3 ≤D≤ 7，同时满足!。

2 分数阶欠阻尼双稳系统

考虑在Gaussian 白噪声激励下，由周期信号驱动的分数阶欠阻尼双稳系统。其系统方程为：

其中r、s表示阻尼系数。这里分数阶导数qD x采用Caputo 定义，满足式（9）。

此外周期信号为：

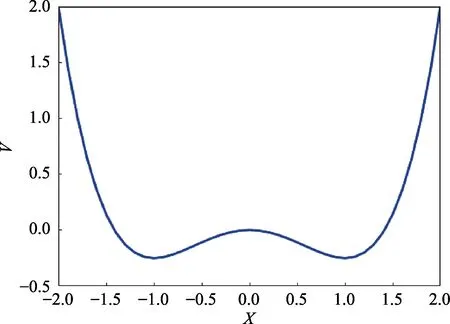
图1 双稳势函数图Fig.1 Bistable potential of system

式中：A为信号振幅；ω为信号频率。为了使得随机共振现象发生较为明显，并满足绝热驱动力相关条件。这里A应满足条件AV＜Δ ，信号频率应小于系统的松弛频率

3 随机共振

在本节中，将引入一种新的方法——统计复杂度方法来度量分数阶系统的随机共振现象。当共振现象发生时，统计复杂度曲线和标准Shannon 熵曲线会变成非单调函数。首先，采用分数阶切比雪夫积分法算法来求解系统[12]；其次计算粒子在势井间跃迁的驻留时间序列；然后利用Bandt-Pompe 算法来提取出驻留时间序列的概率分布，进而得到了统计复杂度和标准Shannon 熵的变换曲线；最后分析不同参数对于系统随机共振现象的影响。文中取嵌入维数d=6，驻留时间序列间隔为M=50 000。

3.1 分数阶导数对系统随机共振现象的影响

如图2 所示，在固定的分数阶导数下，统计复杂度曲线和标准Shannon 熵曲线均呈现出非单调趋势。随着噪声强度的增大，复杂度曲线先增大至波峰，然后减小；相反，Shannon 熵曲线先减小至波谷，然后增大。这些现象说明了在一定的噪声强度处，分数阶系统的复杂性呈现最大值，同时输出信号水平达到最大。这恰好说明在某个噪声强度处，系统发生了随机共振现象，同时，采用数值模拟信噪比指标验证了此现象。此外，图2 表明，不同的分数阶导数下会导致不同强度的随机共振现象。当分数阶导数阶数增大时，统计复杂度和信噪比曲线的波峰不断增大；相反，标准Shannon 熵曲线的波谷不断减小，且波峰和波谷位置均向右移动。也就是说，分数阶导数可以有效地调节随机共振现象的发生，分数阶导数阶数越小，系统越容易发生随机共振现象，即所需噪声强度越小。随着分数阶导数阶数的增大，系统的随机共振现象强度越大，即统计复杂度曲线的波峰最大，标准Shannon熵曲线则相反。总之，分数阶导数阶数的减小可以增强系统的有效阻尼，使得粒子更容易发生跃迁现象，进而发生随机共振现象。

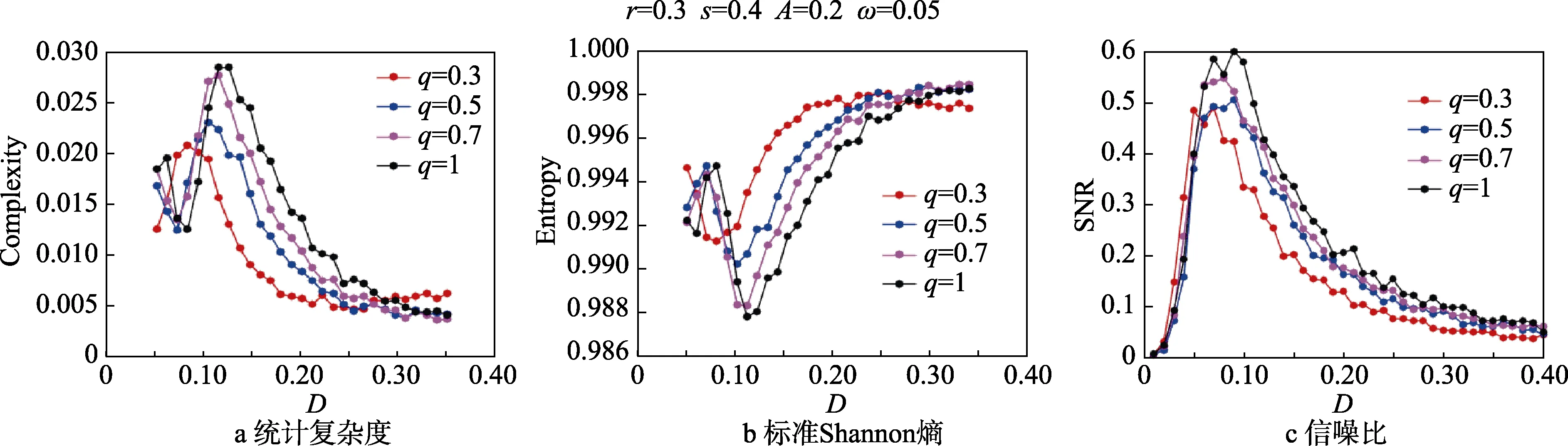
图2 统计复杂度、标准Shannon 熵、信噪比在不同的分数阶导数阶数q 下随着噪声强度D 变化的演化曲线Fig.2 Dependence of statistical complexity (a), Entropy (b) and SNR (c) on noise intensity D for various fractional derivatives with r= 0.3, s= 0.4, A= 0.2, ω=0.05

3.2 阻尼系数对系统随机共振的影响

图3 表明，在固定的分数阶导数下，统计复杂度和标准Shannon 熵曲线均表现出非单调趋势，这种现象表明系统在不同的阻尼系数下均发生了随机共振现象。随着s的增加，统计复杂度曲线的波峰不断降低，而标准Shannon 熵曲线的波谷不断增加，且波峰和波谷位置均向噪声增大的方向右移。此现象表明，分数阶导数前阻尼系数越小，系统越容易发生随机共振现象，系统共振的强度也最大，即阻尼系数可以削弱分数阶系统的随机共振现象。

图3 统计复杂度、标准Shannon 熵在不同的阻尼系数s 下随着噪声强度D 变化的演化曲线Fig.3 Dependence of statistical complexity (a), Entropy(b) on noise intensity D for various damping coefficients with q = 0.7, r = 0.3, A = 0.2, ω =0.05

3.3 信号振幅对系统随机共振的影响

如图4 所示，在固定的分数阶导数下，统计复杂度曲线和标准Shannon 熵曲线均呈现出非单调趋势，说明系统发生了随机共振现象。当信号振幅逐步增大时，统计复杂度指标曲线的峰值缓慢上升；相反，标准Shannon 熵指标曲线的波谷逐渐降低。这些现象说明信号振幅的增大可以增加随机共振现象的强度。总之，信号振幅可以有效地调节分数阶欠阻尼双稳系统的随机共振现象。因此可以选取一个合适的信号振幅使得系统的随机共振现象达到最优，从而对分数阶双稳系统达到良好的动力学控制效果。

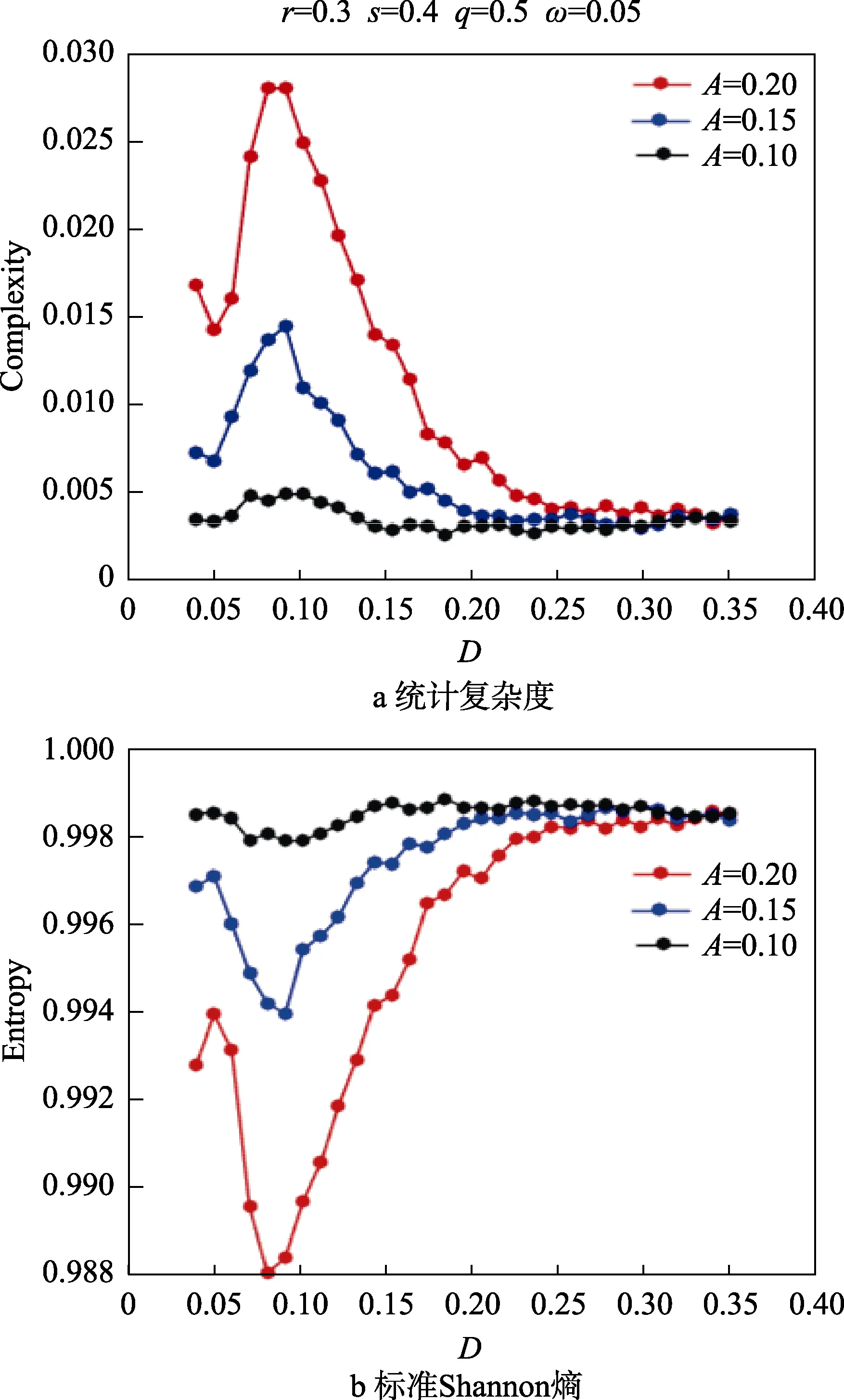
图4 统计复杂度，标准Shannon 熵在不同的周期信号振幅下随着噪声强度D 变化的演化曲线，其它参数为。Fig.4 Dependence of statistical complexity (a), Entropy(b) on noise intensity D for different values of signal amplitude with r= 0.3, s = 0.4, q = 0.5, ω=0.05

3.4 信号频率对系统随机共振的影响

如图5 所示，当信号频率逐步增强时，统计复杂度指标曲线的波峰逐渐降低，相反标准香农熵指标曲线的波谷缓慢上升，且曲线的峰值和波谷位置随着信号频率的增大向着噪声强度增加的方向发生偏移，即信号频率可以削弱随机共振的强度。这里选取的信号频率应小于系统的松弛频率。

4 稳健性

如图6a 所示，首先增加嵌入维数d从4 到6，不管嵌入维数为多少，统计复杂度曲线均为非单调曲线，这说明嵌入维数对此方法没有影响。另一方面，如图6b 所示，取不同的驻留时间序列长度M为10 000、20 000、50 000，同样地，笔者发现驻留时间序列总长度M不会改变复杂度曲线的形状趋势，只是取值大小有所差异。驻留时间序列长度越长，统计复杂度曲线就越光滑。也就是说，此方法需满足条件M≫d!。

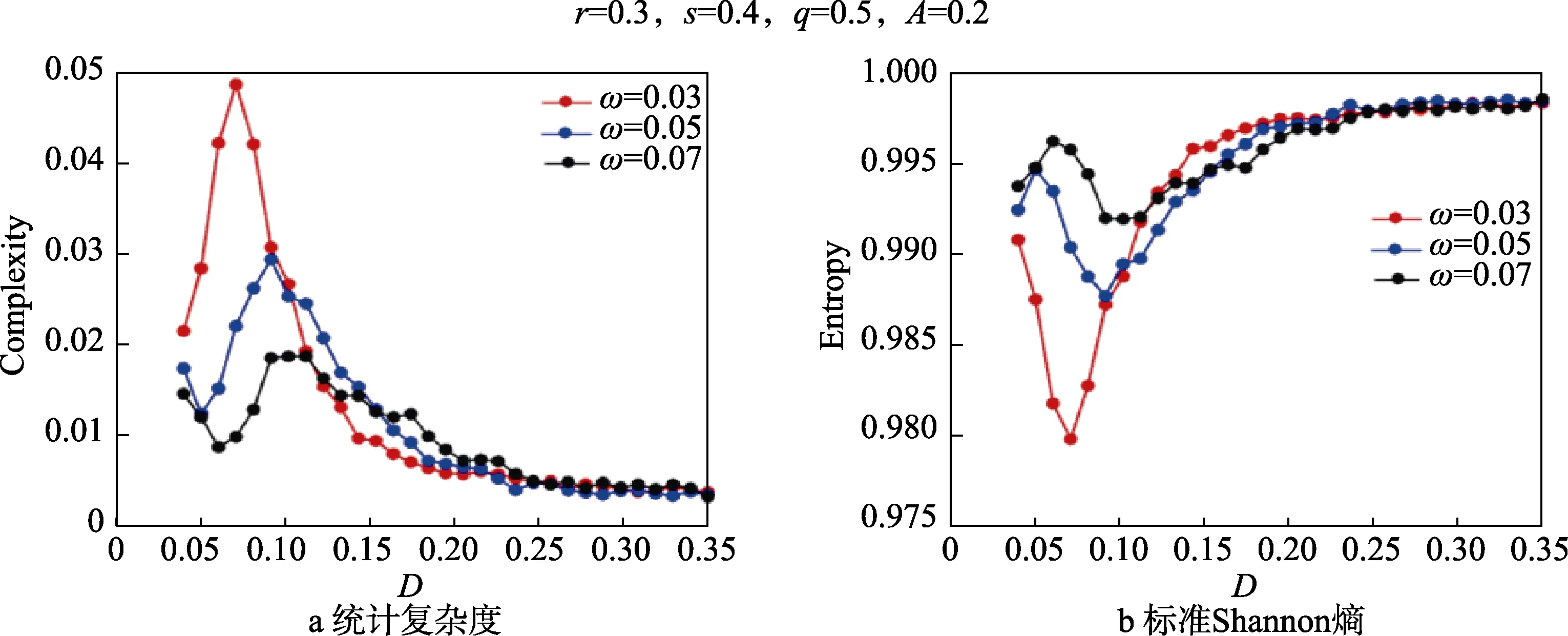
图5 统计复杂度、标准Shannon 熵在不同的周期信号频率下随着噪声强度D 变化的演化曲线Fig.5 Dependence of statistical complexity (a), Entropy (b) on noise intensity D for various values of signal frequency with r = 0.3, s= 0.4, q= 0.5, A=0.2

图6 统计复杂度在不同的嵌入维数和驻留时间总长度下随着不同噪声强度变化的曲线Fig.6 Dependence of statistical complexity on noise intensity D for various embedding dimensions (a) and lengths of the residence time series (b) with r= 0.3, s= 0.4, A= 0.2, ω= 0.05, q =0.7

5 结论

文中引入统计复杂度方法来度量Gaussian 白噪声激励下的分数阶欠阻尼双稳系统的随机共振现象。得出如下结论。

1）在固定的分数阶导数下，统计复杂度指标和标准Shannon 熵指标的曲线均表现为非单调趋势，说明此分数阶双稳系统发生了随机共振现象，且运用信噪比指标函数验证了此方法的准确性。

2）分数阶系统随机共振现象具有更加丰富的动力学行为，且分数阶导数可以有效地调节随机共振现象。信号振幅的增加可以增强随机共振效应，相反信号频率的增大可以削弱此现象。

3）系统的驻留时间总长度和嵌入维数不影响统计复杂度方法的准确性，说明此方法具有稳健性。