基于改进BP 神经网络的网络流量预测∗

吉珊珊 柯 钢

（东莞职业技术学院计算机工程系 东莞 523808）

1 引言

随着计算机网络的深入发展，网络的业务持续增长，由此产生的网络流量约来越多，从而带来了日益严重的网络拥塞问题。网络流量预测是网络QoS 管理的重要依据。实现精准的流量预测，对于精准分析网络带宽状况、提高网络QoS管理的工作效率具有重要的意义［1～2］。

为了提高网络流量预测的精度，国内外许多学者致力于网络流量数据的分析，并提出了多种预测模型。文献［3］提出了一种改进人工蜂群ABC（artificial bee colony）算法优化LSSVM 的网络流量预测模型（ABC-LSSVM）。文献［4］提出了基于ARMA-RESN 的网络流量预测模型，融合回声状态网络和自回归移动平均模型的优点。文献［5］提出了基于小波变换的PCNN 网络流量预测算法。对预处理的网络流量进行小波分解，利用PCNN 模型预测获得的近似系数和细节系数，通过小波逆变换对预测的小波系数进行重构，得到预测的网络流量。文献［6］提出了将灰色系统理论和马尔科夫链相结合的流量预测方法，取得了较高的预测效果。

神经网络是一个具有高度非线性的动力学系统，具有非线性拟合能力。针对标准的BP 神经网络在网络流量预测过程中存在收敛速度慢、易陷入局部极小值的缺点，本文引入了引入动量因子和自适应学习速率来改进BP神经网络。模型的仿真结果表明，改进的BP神经网络预测的结果误差更小，精确度高，训练次数少，具有较高的实际应用价值。

2 BP神经网络

机器学习中，模仿生物神经网络结构的神经网络算法可以说是当下使用最广泛的算法，而其中误差逆传播算法（BP）又是神经网络中最有代表性的算法，也是迄今为止使用最多、最成功的算法。

BP 神经网络［7～10］是一种多层前馈神经网络，由输入层、隐含层和输出层组成，如图1所示。

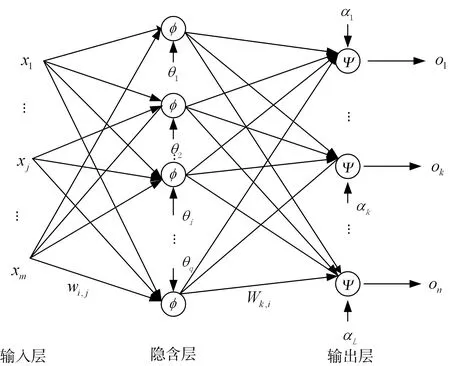
图1 BP神经网络结构

图1 中，xi表示输入层第i 个节点的输入，i=1,…,M；wi,j表示隐含层第i 个节点到输入层第j 个节点的权值；θi表示隐含层第i 个节点的阈值；φ 表示隐含层的激励函数，令其为Sigmoid 函数；wk,i表示输出层第k 个节点到隐含层第i 个节点的权值，i=1,…,q；ak表示输出层第k 个节点的阈值，k=1,…,L；Ψ 表示输出层的激励函数，令其为Sigmoid 函数；ok表示输出层第i 个节点的输出。

BP 的核心思想是通过调整各神经元之间的权值和阈值，使得模型输出逼近实际输出。此过程可分为两个阶段：先实现输入信号的正向传播，再实现误差的反向传播。因此，BP 算法的核心步骤如下：先求得在特定输入下实际输出与理想输出的平方误差函数；再利用误差函数对神经网络中的阈值以及连接权值进行求导，求导原则就是导数的“链式求导”法则；最后根据梯度下降算法，对极小值进行逼近，当满足条件时，跳出循环。具体的计算过程如下。

1）信号正向传播

隐含层第i 个神经元的输入Hi(i)：

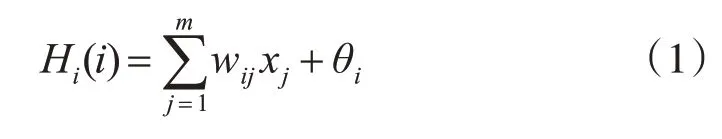
隐含层第i 个神经元的输出Ho(i)：

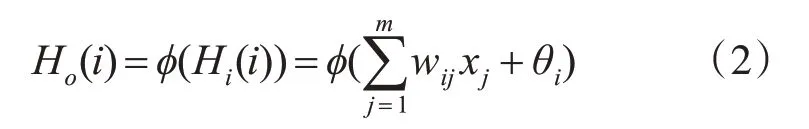
输出层第k 个神经元的输入Oi(k)：

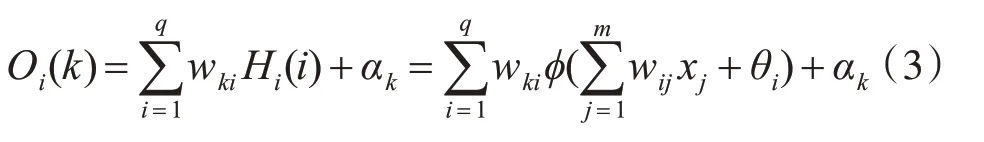
输出层第k 个神经元的输出：

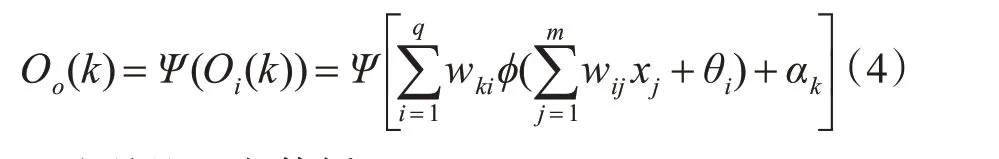
2）误差反向传播

输入样本中的输入节点xj经由前馈网络传递所产生的输出节点的输出ok与样本中所期望输出Tk之间存在着误差，其平方型误差函数为

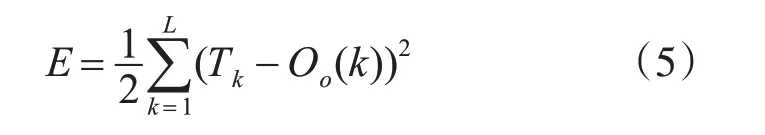
输出层权值调整公式为

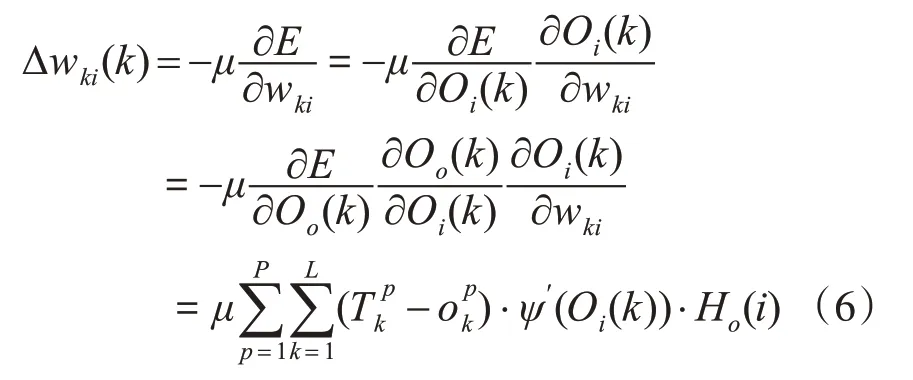
输出层阈值调整公式为

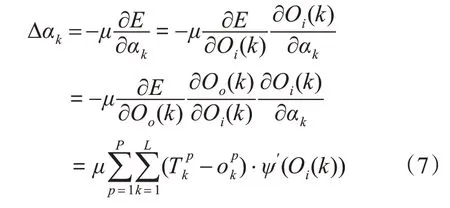
隐含层权值调整公式为

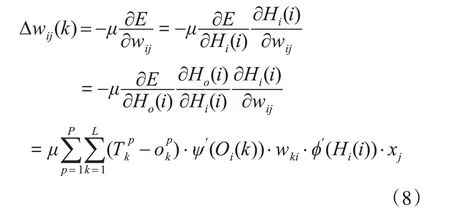
隐含层阈值调整公式为

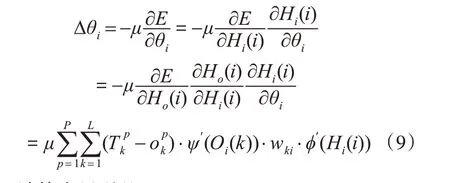
计算全局误差：

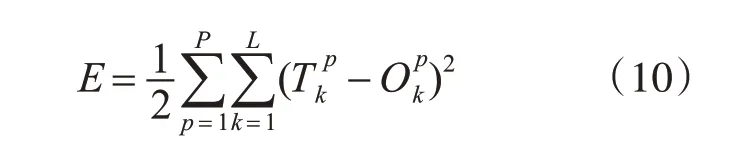
判断全局误差是否满足要求，当误差达到预设精度或者学习次数大于设定的最大次数，则结束算法。否则，选取下一个学习样本及对应的期望输出，进入下一轮学习。

3 改进BP神经网络

由于BP神经网络采用线性规划中的梯度下降方法，按误差函数的方向修改权值和阈值，常常存在以下问题：1）在训练过程中收敛速度慢。2）易陷入局部极小值状态。针对以上问题，本文从以下两个方面对BP神经网络算法进行了改进。

3.1 增加动量因子

BP 神经网络在修正其权值时，往往不考虑之前的梯度方向，只从梯度下降的方向进行权值调整。这样会导致BP神经网络在学习过程中发生振荡，从而陷入局部最小值。本文引入了增加动量因子的方法［11～12］，该方法是在反向传播法的基础上在每一个权值（或阈值）的变化上加上一项正比于前次权值（或阈值）变化量的值，并根据反向传播法来产生新的权值（或阈值）变化。带有动量因子的权值（或阈值）的调节公式为

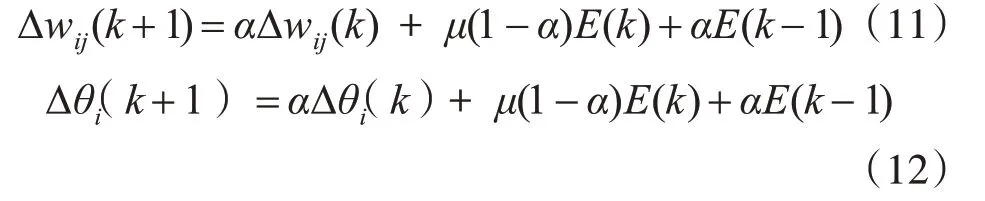
式中，μ 为学习因子，0＜μ＜1；α 为动量因子，0＜α＜1，一般取0.8。

3.2 自适应学习速率

学习速率取值非常重要。取值过大时，收敛速度快，但会引起权值振荡；取值过小，收敛速度慢，训练时间太长。本文引入了一种自适应学习速率，判断检查权值是否真正降低了误差函数，如果降低了，就表明学习速率低，这时就增加学习速率；如果没有降低，反而增大了误差函数，就表明学习速率高，这时就减小学习速率［13～14］。下面给出了一个自适应学习速率的调整公式为

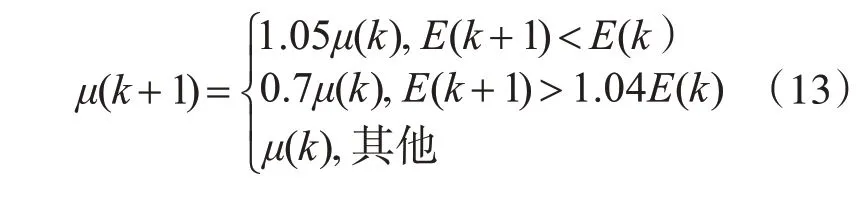
4 仿真实验

4.1 数据来源

网络流量数据来源于BellCore 实验室的高分辨率流量数据（BC-pAug89）［15］，收集了从1989 年8 月29 日11：25 分开始的大约3142.82s 内捕获的100 万个数据分组。考虑到网络流量的时间相关特性，我们对数据进行了预处理。以1s 为采样周期，把每一秒的网络流量数据进行加和统计，得到3142 个样本数据。这些数据组成了一个网络时间流量序列{x(t),t=1,2,…3142}，网络流量时间序列数据如图2 所示。

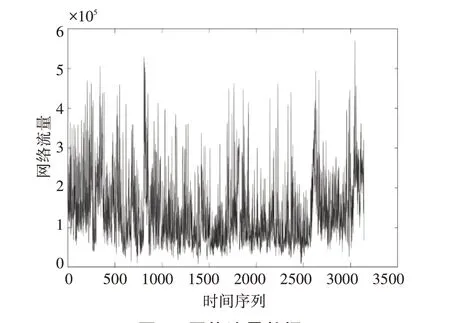
图2 网络流量数据

4.2 数据预处理

由于BC-p Aug89 数据集的网络流量存在变化范围较大的特点（其中最大值与最小值有好几个数量级的差距），因此对其进行了归一化预处理，如图3所示。

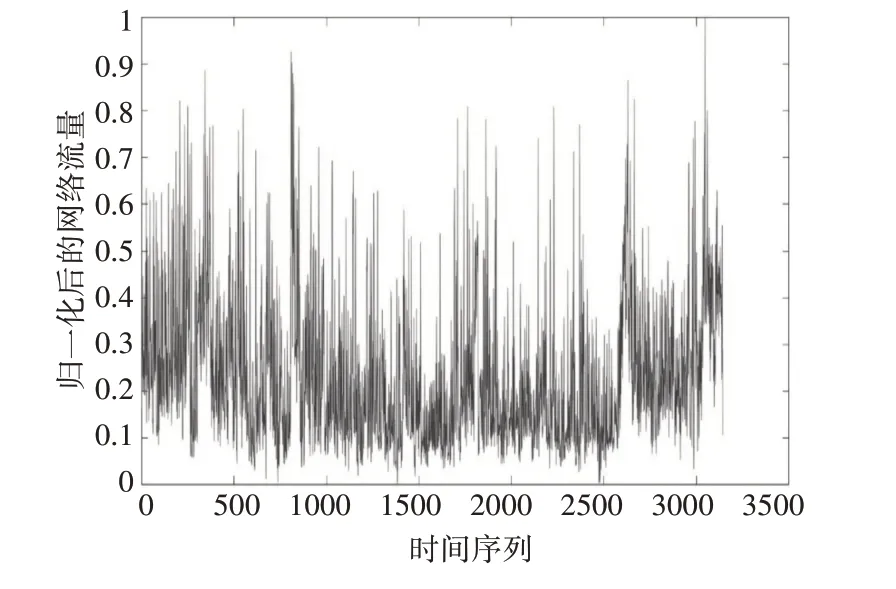
图3 归一化后的BC-p Aug89数据集

将该数据集划分成训练集和测试集两部分，每组训练样本数据包含共4 个时刻的流量数据，即以当前时刻之前4 个时刻的网络流量数据来预测当前时刻的网络流量数据。训练集包含3000 个样本，测试集包含138个样本。

4.3 实验结果分析

4.3.1 参数设置

本文实验的BP 网络采用5-11-1 的机构，即网络的输入节点数为5，隐层神经元为11 个，输出节点数为1。神经元之间的激励函数采用非线性激励函数Sigmoid 函数。动量因子α=0.8，学习率μ=0.01，最大迭代次数为100，收敛精度为0.00001。其他参数均为缺省值。

4.3.2 实验结果分析

按照4.3.1 节的参数设置，建立改进BP 神经网络的网络预测模型，并对网络流量训练样本进行拟合。从图4 中可知，预测曲线与实际流量曲线的趋势几乎一致。

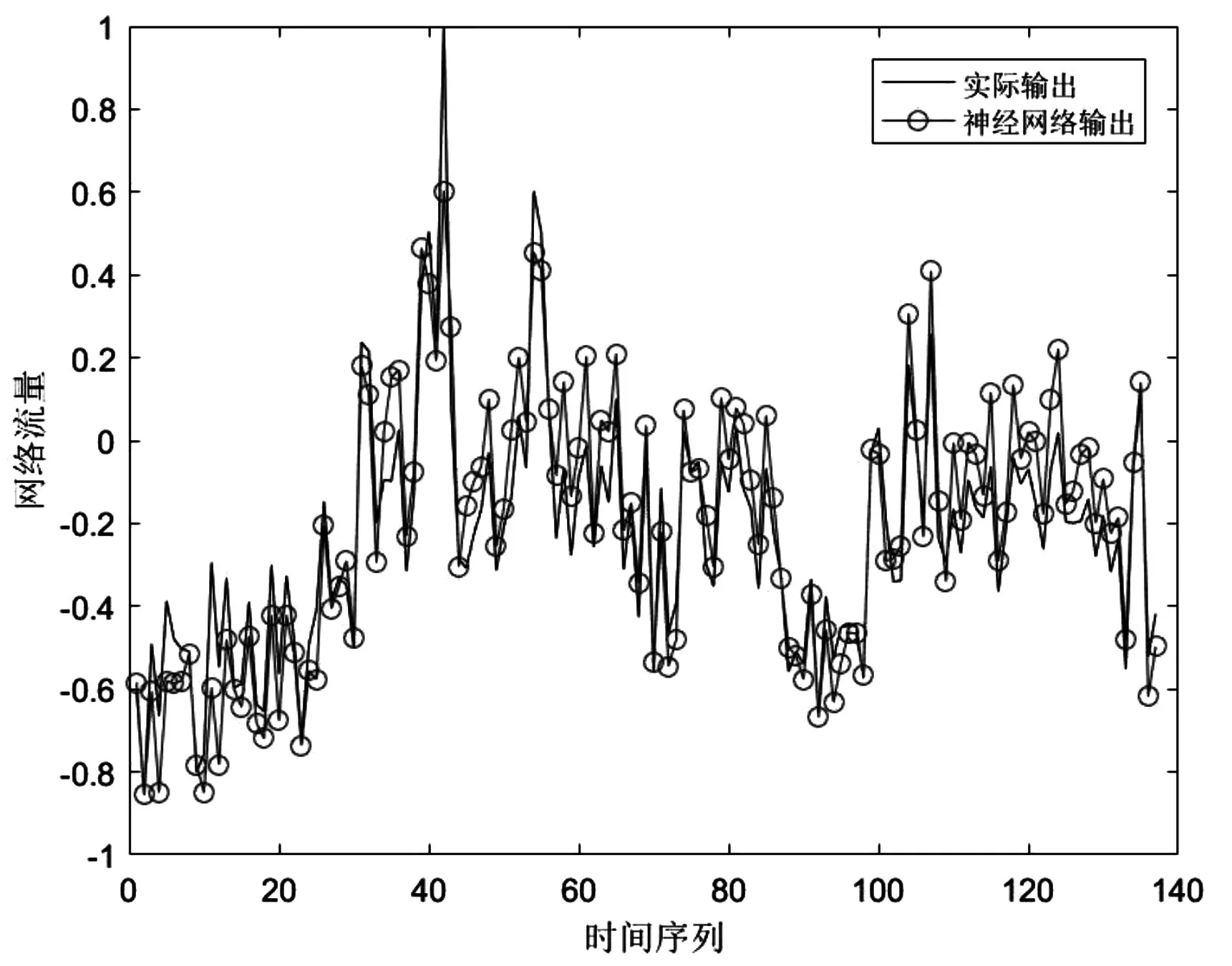
图4 改进BP神经网络的网络流量预测结果

为了进一步评价预测方法的性能，本文引入了RMSE（均方根误差）和MAPE（平均绝对百分率误差），这两项指标可以反映预测值与真实值之间的整体偏差估计。对预测效果进行整体的评估，这两项指标值越低，表示模型的预测精度越高。它们的计算公式如下：

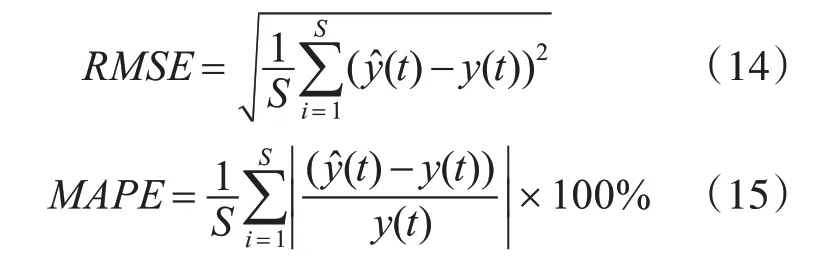
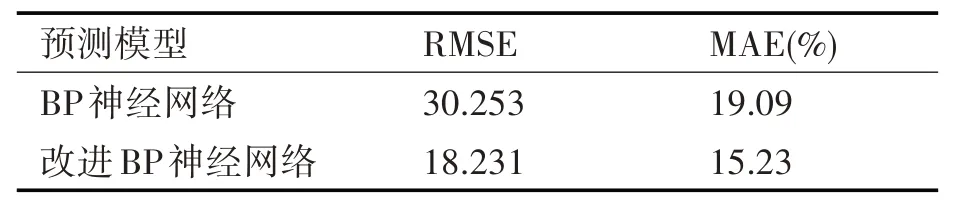
表1 各种方法预测性能对比

从表1可知，相对于BP神经网络，改进BP神经网络无论预测精度、泛化能力均取得更加理想的结果。

5 结语

本文针对BP神经网络在网络流量预测过程中存在收敛速度慢、易陷入局部极小值的问题，提出了一种改进BP神经网络的网络流量预测模型。该模型引入了动量因子和自适应学习速率。仿真结果表明，改进BP 神经网络改善了算法后期的收敛速度、局部搜索能力弱的缺点，提高了网络流量的预测精度。