改进的道格拉斯-普克算法在电信代维系统的应用∗
2020-10-09李晓妍
周 腾 李晓妍
(1.中国科学院合肥物质科学研究院 合肥 230031)(2.中国科学技术大学 合肥 230026)(3.江苏海事职业技术学院 南京 210000)
1 引言
随着移动终端的飞速发展,GPS 技术的不断进步,智能手机已成为一种非常普遍的设备[1],广泛应用于通信设备看护和通信线路巡检中。在电信综合代维管理系统中,这些智能设备能够采集代维巡检人员移动线路的GPS轨迹的经纬度信息,并通过4G 移动网络传输到后端服务器中,系统会自动与预先设定的巡检范围进行适配,通过加强对代维巡检人员的管控力,提高巡检质量。同时,移动设备所采集到的GPS 经纬度信息也呈现出一种爆炸性的增长趋势[2],大量的数据不仅极大地影响了系统的存储效率,占用了较多的运算资源,也影响了前端的浏览体验。因此,研究如何将GPS经纬度信息进行压缩存储势在必行,既从算法方面进行改进,一方面要能够在轨迹保存完整的情况下,简化轨迹数据,以提高存储资源的利用效率;另一方面要通过压缩数据,减轻运算复杂度,提高读取效率,以改善前端展示时的用户体验。
2 GPS轨迹压缩算法——道格拉斯-普克算法
轨迹数据压缩算法一般分为两类[7],一是将运动轨迹进行分段线性化[3],由于其算法形式简单,计算复杂度低,是目前最为常用的算法;二是非线性的轨迹拟合[4],如Bezier曲线,非线性拟合更接近真实轨迹,但是其算法复杂,计算量大。由于电信代维巡检中的人员轨迹是沿电信线路或者巡检道路而记录的,所以使用线性压缩算法更能够贴合现实中的情况,而且也能够节约一部分运算资源。在众多线性压缩算法中,道格拉斯-普克算法最具有代表性。
道格拉斯-普克算法(Douglas-Peucker Algorithm)[5]简称DP 算法,在1973 年由Douglas 和Peucker提出。该算法步骤如下:
1)在轨迹曲线首尾两点A、B 之间连接一条直线AB,该直线为曲线的弦;遍历曲线上其他所有点,求每个点到直线AB的距离,找到最大距离的点C,最大距离记为dmax;
2)比较该距离dmax与预先定义的阈值Dmax大小,如果dmax<Dmax,则将该直线AB 作为曲线段的近似,曲线段处理完毕。
3)若dmax>Dmax,则使C 点将曲线AB 分为AC和CB两段,并分别对这两段进行1)、2)步处理。
4)当所有曲线都处理完毕时,依次连接各个分割点形成的折线,即为原始曲线的路径。
该算法结构简单,效率相对较高[6]。但它是一种需要明确起点和终点的后压缩方法,是一种离线压缩方法。而在电信代维系统中,数据需要实时进行处理,DP 算法在代维系统这种场景中并不能有效适用。因此,需要对该算法进行改进,使其能够对这些数据进行实时压缩处理。
3 改进的道格拉斯-普克算法
3.1 轨迹采集方式改进思路
DP 算法是一种离线后压缩算法,需要明确知道曲线的起点和终点,而代维系统中的GPS轨迹记录是实时传输数据,需要一种在线实时的压缩算法,因此,需要在DP算法的基础上进行改进。
由于代维系统中线路巡检的轨迹是有折返的,实时数据量庞大,因此算法改进时需要考虑以下三个问题。
其一,相同经纬度的记录点冗余问题。当巡检遇到设备检查点时,巡检人员会在此处停留,轨迹偏移量便会大大减少,甚至会出现多次上报的数据经纬度值相同的情况,造成大量数据冗余。这部分数据若是运算后再进行剔除,会加大计算资源的耗损[7],因此应在运算前进行预处理比较筛选,减少计算量。
其二,计算模型问题。地理空间距离的计算中含有大量的三角函数运算[8],对计算资源的消耗较大。一般来说,地球上两点之间的距离计算有以下两种模型[9]:一是球面模型。这种模型将地球看成一个标准球体,球面上两点之间的最短距离即为圆弧长,这种方法使用较广,逻辑相对简单,消耗的CPU 计算资源较少。二是椭球模型[9]。这种模型最贴近真实地球,精度较高,但计算较为复杂,需要耗费更多的CPU 运算资源[10]。根据电信巡检业务需求特点,对GPS 轨迹精度并无高精度要求,因此应采用球面模型来计算地理空间距离以减少运算资源的消耗。
其三,共线轨迹点记录存留问题。因轨迹是有折返的[11],即出现三个GPS轨迹点在同一条直线上的情况,则需要对三点共线的情况进行讨论,如果巡检方向一致,应该舍弃位于中间的点;如果巡检线路出现折返,则必须全部保留。这样既能保证轨迹完整性,又能够有效减少数据冗余。
因此,改进的DP算法步骤如下:
1)将GPS 轨迹记录上的某一点记为第一点A,与相邻的下一个记录点进行比较,若两点经纬度数据完全一致,则删除下一点的记录,再将A 与下一个记录进行比较,依次筛选,排除经纬度数据完全相同的冗余点,直至记录点与A 经纬度数据不同,记为点B。
2)按照步骤1 的方法,找到与点B 经纬度数据不同的记录点C。
3)在AB 之间连接一条直线,计算点C 到直线AB的欧式距离d。
4)若距离d=0,则A、B、C 三点共线。根据经纬度信息,判断C 点是否位于A、B 两点之间,若是,则保留C点数据;若否,则删除B点数据。
若距离d 小于阈值,则删除C 点数据。重复步骤2),寻找下一C点。
若距离d 大于阈值,则保留C 点数据。将记录点B作为第一点,重复步骤1)、2)、3)、4),直至工单记录结束。
3.2 GPS轨迹两点间距离的计算优化
在轨迹记录距离计算时,有大量的三角函数计算,占用了较多计算资源,影响系统运行速度,因此对此进行计算优化。
根据球面计算模型,在GPS轨迹上有任意两点A、B,设φ1、φ2为AB两点的纬度,ω1、ω2为两点的经度,R为地球球面模型的半径,Δω、Δφ分别为AB两点的经、纬度差,这两点的圆心角σ 可通过球面余弦定理[12]得出:

根据弧长公式可得A、B 间的球面距离:d=Rσ 。如果A、B 之间距离很短,即d 相对于R 很短时[13],A、B 间的圆心角很小,cos Δω余弦函数无限趋近于1[9],那么上述的反余弦函数就会出现较大的舍入误差。为避免这种情况的出现,利用正弦函数的haversine 公式来进行公式变形计算地球表面距离。这样即便距离很近值很小,也能保持足够的有效数字。

在实际应用中,GPS 轨迹记录采集的密度较高(30s/次),而代维巡检人员的行走速度不会超过20km/h,因此,可以认为经纬度偏移值较小即
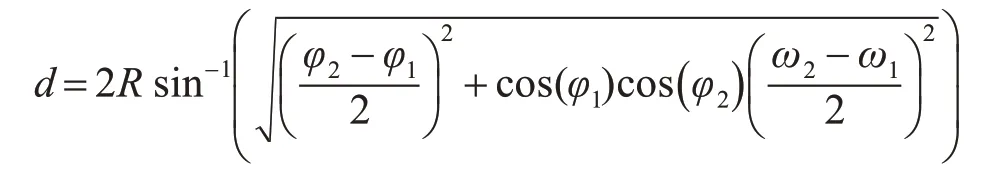
3.3 偏移值d的计算
根据上述内容,GPS 轨迹记录会出现记录点共线的情况,要对此进行判断。因此,需要分别计算AB、AC、BC 的距离。为避免三角函数运算,本研究采用海伦公式[14],根据三点构成的三角形来计算欧式距离d。设S 为三角形ABC 的面积,AB 为底,d 则为三角形的高。根据三角形面积公式,可知:d=海伦公式如下所示:

其中,a=AB,b=BC,c=AC,p 为三角形的周长的即
因此:

4 算法实验与仿真
本研究对改进后的算法进行数据检验。从数据库中随机抽取了30s采集一次的500条线路巡检工单,共计25231 条记录作为测试数据,利用面向对象的python语言对算法进行编程。
4.1 压缩比测试
对上述工单进行压缩处理。选取4 个阈值进行比较。压缩比如图1所示。

图1 不同阈值下的压缩比
可见,运用改进的DP 算法,在阈值为20m 时,压缩比取得了非常良好的压缩效果,压缩比达到5.31,若实际应用到系统中,将大大减少工单记录数据量,减轻存储压力[15],提高存储读取效率。
4.2 压缩轨迹展示示例
选取一条有85 条记录的工单,并采用5m、10m、15m、20m 四种阈值进行压缩处理,处理后轨迹如图2~6所示。

图2 原始轨迹记录(30s/次采集)

图3 采用5m阈值处理的轨迹

图4 采用10m阈值处理的轨迹

图5 采用15m阈值处理的轨迹

图6 采用20m阈值进行处理
可见,在不同的阈值下,线段的基本都能够清晰保存GPS 轨迹记录,且随着阈值的扩大,线段化的明显越来越明显。仿真实验证明能够满足线路巡检业务的需要。
5 系统应用
经过仿真实验结果和业务中精度的需求的综合考虑,在江苏移动综合代维系统中进行实地应用。运用改进的DP算法,采用10m作为阈值,对工单进行处理。首先对2018年8月的数据进行处理,并与原数据进行离线后比较。经比对,8 月GPS 轨迹记录数据量可减少70%,前台加载渲染速度提高近50%,达到了较为预期满意的效果。此后,又将此算法应用到2018 年9 月数据的实时处理中。同比数据量下降77%左右得到的相对满意的效果。
6 结语
本研究采用了改进后的DP 算法,对GPS 轨迹记录进行压缩,使其适应电信业务中的实时压缩要求,并进一步讨论了节约运算资源并提高运算速度的方法。经过实验测试,证明该算法能够在提高压缩比的情况下,满足轨迹展现管理的要求。通过这一算法,能够显著减轻服务器的存储和渲染负担[16],进一步提升了用户体验。本研究对电信人员巡检轨迹和看护轨迹的压缩和存储方面有一定的参考价值。
