基于改进型蚁群算法自适应停车引导系统的设计

2020-10-08晏勇，雷航，梁潘

实验技术与管理 2020年3期

晏勇，雷航，梁潘

（1. 阿坝师范学院电子信息与自动化学院，四川阿坝 623002；2. 电子科技大学信息与软件工程学院，四川成都 610054；3. 成都航空职业技术学院士官管理学院，四川成都 610100）

目前，停车难已经成为阻碍城市发展的重要因素，特别是在城市中心繁华地段这一矛盾更加突出。停车场信息化建设滞后与汽车产业的发展不相称，停车缺乏有效引导设备，车辆不能及时高效找到停车位，同时停车场本身通行能力有限，容易造成拥堵，停车更难。本文采用改进蚁群算法[1]，设计了一种自适应停车引导系统，车辆进入停车场后，系统按目的地最优路径原则引导车辆就近停放，缩短了停车路径，减少了停车时间，提高了停车效率与停车场的使用效率，具有很高的实用价值。

最优路径规划是自适应停车引导系统的核心，预停车辆进入停车场后迅速找到目标停车位，完成停车。蚁群算法是一种典型的最优路径规划算法，有并行性、鲁棒性强等优点，同时也存在局部最优与收敛性差的缺点[2]。文[3]研究了基于人工势场的群蚁算法，采用随机参数转移策略，增强算法鲁棒性；文[4]重构启发函数，加快算法收敛速度，但容易出现局部最优；文[5]将基本蚁群算法与遗传算法相融合，引入交叉算子，避免局部最优。本文针对标准蚁群算法缺点，结合先前研究成果提出了基于状态转移策略的改进型自适应蚁群算法，加快算法收敛速度，实现停车最优路径规划。

1 任务描述

典型地下停车场有一个出口与一个入口，受建筑物实际条件影响，停车场内部存在断头路，内部道路为双向两车道行驶，考虑安全因素需减少步行时间，目的地设置为大楼电梯口，车辆进入停车场后，引导系统按目的地最近原则分配车位，尽量远离停车场出口且转弯少，按路径最优原则规划一条停车路径，在入口大屏幕显示，并通过蓝牙模块发送至车主手机，所有车主按照停车场引导路径与引导车

位有序停车。基于以上特征，采用拓扑法对典型的停车场进行描述，拓扑结构如图1。

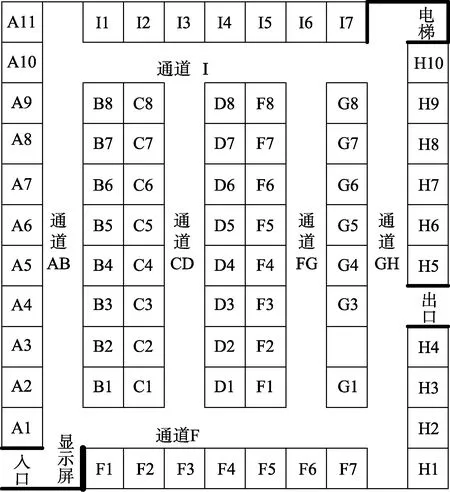
图1 停车场拓扑结构

停车引导系统中有n辆待停车辆，有n个车位，车辆停车最优路径优化模型用有向图表示，其中G=(V,A)，V= 0∪D，入口0 表示车辆起始位置；D为车辆与空闲车位集合，D=B∪C= ｛1,2, … , 2n｝；B为车辆集合，B= {1,2,… ,n}；C为空闲车位集合，C={n+ 1,n+ 2,… , 2n}；A= {(i,∈V,i≠j,i,j= 0,1,… ,n}，每条路径(i,j)都包含非负权属值，dij和tij分别代表停车路径的距离和时间。汽车从入口0 出发，到达指定停车位[6]。根据停车场现场条件与任务描述，停车引导系统最优停车路径与时间成本的目标函数如式（1）：

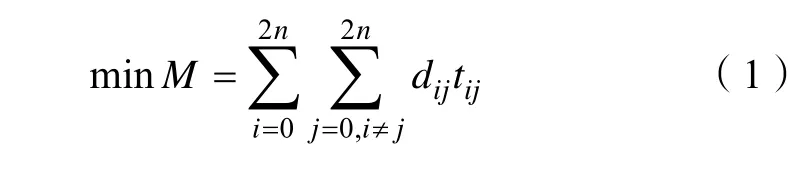
2 改进型自适应蚁群算法

2.1 算法描述

改进型蚁群自适应算法以原有信息素更新为基础，计算下一节点移动转移策略，求解最优停车规划路径，同时保证收敛速度与质量，提高算法鲁棒性[7]。最优规划路径搜索中的蚂蚁k在时刻t处于节点i，由改进型自适应蚁群算法状态转移策略计算下一移动节点j，通过规划最优路径到达停车地点[8]。

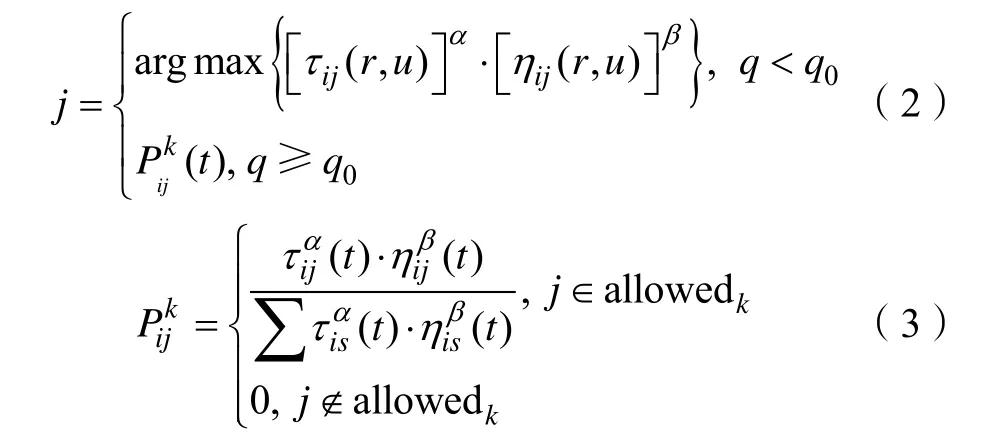
式（2）和（3）中，k表示蚂蚁数量，allowedk表示蚂蚁可访问下一节点的集合，表示节点i的第k只蚂蚁在下一节点转移到节点j的概率，α表示信息素的重要程度，β表示启发因子的重要程度[9]。q∈ [ 0,1]为平均分布随机数，q0为阀值决定先验知识与新路径之间重要程度。q＜q0则蚂蚁采用确定性搜索方式移动；q≥q0则蚂蚁采用随机搜索方式移动，通过计算下一点概率确定下一步移动节点[10]。由于地下车库停车过程中可能受到停车场拥挤等因素干扰，进一步进行滤波与最佳路径自适应调整，滤波系统函数为

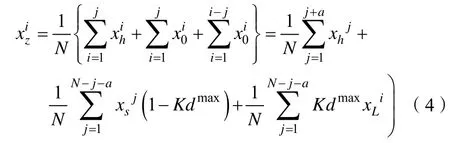
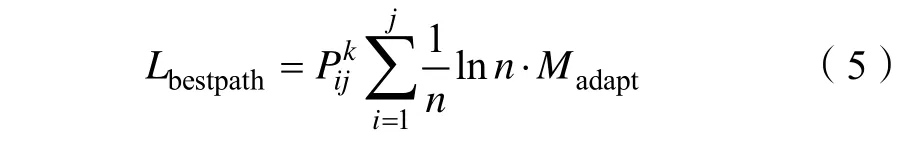
停车拥堵检测采用激光器检测停车路径是否拥堵，双向拥堵时Madapt= 0，单向拥堵时Madapt= 0.5，双向畅通时Madapt= 1。

2.2 算法流程

算法设计基于下一步潜在节点移动的状态转移策略，设定蚂蚁的自适应度，求解蚂蚁最优路径，改进型自适应蚁群算法流程图2。

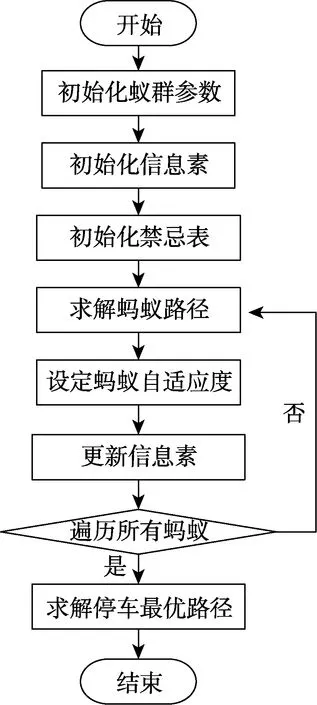
图2 改进型自适应蚁群算法流程

初始化蚁群参数包括蚁群数量、迭代次数等参数，令初始循环次数为0；将m只蚂蚁放置于停车场入口处作为初始节点[12-13]，初始化信息素nij=，将初始节点作为出发点搜索下一步移动节点；初始化禁忌表以蚂蚁当前位置为中心搜索下一步移动节点，按照式（2）和（3）计算路径概率，将下一移动节点添加至遗传禁忌表，搜索蚂蚁移动路径；通过设置Madapt，更新信息素遍历蚂蚁路径，求解蚂蚁移动最优解，即停车最优路径[14-15]。

3 系统实现

改进型蚁群算法的自适应停车引导系统由4 个部分构成，即停车场主控平台、拥堵检测终端、车位检测终端、智能手持终端。停车场主控平台为系统核心，完成改进型蚁群算法的停车系统的自适应算法并选择最优停车路径、待停车辆与停车路径绑定、待停车辆路径与智能手持终端绑定，无线传感器网络（wireless sensor networks, WSN）协调器组网与网络管理[16]。停车场主控平台采用德州仪器C6000 系列66AK2E0x 多核DSP 处理器，主频1.4 GHz，内嵌ARM 内核；WSN协调器与终端节点控制器采用基于TI 公司Zigbee 协议处理器CC2530[17]。

4 结果与分析

改进型蚁群算法自适应停车系统仿真测试包括最优停车位选择与最优停车路径选择，以某地下停车场为例，采用MATLAB2018a 软件进行仿真与数据对比测试，数值仿真环境为Intel Core i7-8700 处理器、8 GB内存、Windows10 操作系统[18]。

4.1 最优停车位仿真测试

改进型蚁群算法自适应停车系统最优车位为靠近电梯入口且远离停车场出口的位置，每一个车位都作为WSN 终端节点，有唯一物理地址，计算电梯入口与车位距离LEe、停车场出口与车位距离LPe。对于1和 2 号停车位，LEe1＞LEe2则选择 2 号停车位，LEe1＜LEe2则选择1 号停车位，即选择靠近电梯入口的停车位；当LEe1=LEe2时，LPe1≥LPe2则选择1 号停车位，LPe1＜LPe2则选择2 号停车位，即选择远高停车场出口的停车位。

停车场平面图如图1 所示，当前实际空余车位A11、C5、G5、I7、H10，通过仿真计算得到 LEeA11＞LEeC5＞LEeG5＞ LEeI7= LEeH10和 LPeI7＞LPeH10，选择I7车位，实际大屏幕显示车位与仿真测试结果一致，下一步完成最优停车路径仿真测试。

4.2 最优停车路径仿真测试

停车场平面图如图1，仿真测试蚁群算法参数为蚂蚁数量M= 50，迭代次数I=100，α= 1，β= 1，τ0= 1，学习速率η=0.8，根据不同拥堵情况设定Madapt，每个实验样本均为随机生成，起点为停车场入口，终点为停车位I7，汽车进入停车场限速5 km/h，车位尺寸3 m ×6 m，停车场路面双向车道路宽8 m。Madapt= 1时基本蚁群算法与改进型自适应蚁群算法结果对比见表 1；Madapt= 0.5时结果对比见表 2；Madapt= 0时结果对比见表3。

表2 基本蚁群算法与改进型自适应蚁群算法结果对比（Madapt=0.5）

表3 基本蚁群算法与改进型自适应蚁群算法结果对比（Madapt=0）

对比分析表1、2、3 结果知，停车路径双向畅通时，相比基本算法，改进型蚁群自适应算法时间与距离短且弯道少；通道AB 单向拥堵时，原最优路径“入口—AB—I—I7”经自适应调整后变为“入口—F—CD—I—I7”，停车时间减少39 s；通道AB 双向拥堵时，基本蚁群算法停车路径“入口—AB—I—I7”不变，停车时间待定（等待交通恢复），经自适应调整后最优路径为“入口—F—CD—I—I7”，停车时间45 s。经测试，改进型蚁群自适应算法在交通畅通、单向拥堵或双向拥堵情况下均能自动检测拥堵并识别最优停车路径，汽车可按最优路径停入车位。