含噪图像的快速超分辨率重建算法
2020-10-08王庆成杨亚楠
温 佳,王庆成,杨亚楠,李 楠
(天津工业大学 电子与信息工程学院,天津 300387)
单图像超分辨率重建是图像处理领域的经典研究内容。一般来说,它的首要任务是从低分辨率图像中重建丢失的高频细节。传统的基于插值的超分辨率重建技术[1-2]已经被广泛运用并具备快速实现的优点。但是,面对图像边缘、不连续区域、高频特征时,往往不能取得理想的效果。近年来,人们提出了许多具有影响力的基于实例的超分辨率重建方法[3-5],并取得了不错的效果,逐渐成为超分辨重建领域的主流方法。该方法的主要思路是:学习样本库中对应高、低分辨率图像块之间的映射关系并结合输入的低分辨率图像块重构出丢失的高频细节。大多数方法[6-7]都是基于最近邻嵌入思想。总的来说,针对每一个输入的低分辨率图像块从数据库中寻找最为接近的k个图像块,再结合之前学习的映射关系完成相似块的线性组合,最终估计出高分辨率图像块。虽然这些算法可以得到不错的结果,但是难以确定的近邻数目还是降低了这类算法的稳定性。为了解决这个问题,动态k近邻算法[8]人为提出了一种相似判断依据,从而可以动态地确定近邻数目。Yang 等[9]利用稀疏编码实现了图像的超分辨率重建。该算法假设高、低分辨率图像具有相同的稀疏表达,并通过高、低分辨率字典的耦合训练确保具有相同的稀疏系数。它通过对输入图像块的稀疏表达解决了近邻数目的选择,从而取得了令人印象深刻的结果。Zeyde 等[10]通过正交匹配和降低维数的方法进行稀疏系数的求解,从而提高了效率。除此之外,研究表明在不同尺度间,图像结构往往会出现重复。利用自然图像中结构的自相似性[11-12],可以直接从输入图像本身获得重建信息而不再依靠外部数据库。但是,为了获得理想重建质量,不可避免地消耗过多的内存和计算时间。虽然这些算法可以获得较好的性能,但都假设输入图像不含有噪声,这并不符合实际情况。目前,对含噪图像的超分辨率重建领域的研究较少。Xie 等[13]通过自适应正则化滤波器来滤除输入图像中的噪声,但是去噪过程中产生的伪影会在重建过程中被放大。基于目前的研究现状,本文致力于减小在重建过程中噪声的影响从而提高算法的鲁棒性。由于稀疏表达可以使信号能量仅仅集中在个别原子上,因此对噪声图像具有一定的鲁棒性。另一方面,综合字典(如K-SVD 字典)通过实例图像的学习可以重构出复杂的局部结构,但是也将消耗大量的计算时间。

图1 算法流程图
受此启发,本文引入稀疏理论来降低噪声的影响并通过新的相似块选择方案来提高重建速度。具体过程如图1 所示。整个过程大致可以分为3 个阶段:第一阶段是字典训练阶段,首先,训练中的高、低分辨率图像块具有相同的尺寸大小,后者是通过训练图像先下采样后插值放大,最后通过图像分块得到的。并且训练图像是无噪声的,即训练过程不受输入图像噪声程度的干扰。由于高分辨率字典是由对应的高、低分辨率图像块共同训练得到的,因此它不仅表示高分辨率图像的高频细节,还表示无噪声低分辨率图像的纹理结构。第二阶段是高分辨率图像块重建阶段,重建高分辨率图像块的关键在于找到相似的高分辨率图像块并完成合理的线性组合。首先,根据输入的特征向量可以从匹配对象中自适应地选择k个相似的字典原子对();并计算他们和输入特征向量之间的相似度差异di。结合输入的特征向量、低分辨率字典原子、相似度差异di计算出对应权值ωi。其次,通过计算可以得到估计的高分辨率图像块和去噪后的低分辨率图像块。再次,利用所有的估计图像块并通过对重叠区域的平均计算,得到估计的高分辨率图像和去噪后的低分辨率图像。最后,结合迭代反投影(IBP),得到最终重建的高分辨率图像X*。
1 含噪图像的快速超分辨重建算法
图像的退化过程通常可以描述成公式(1)。低分辨率图像Y∈RM×M,是高分辨率图像X*∈RN×N经过下采样和模糊退化得到的。

其中:D为下采样因子,B为模糊算子,n为在算法处理过程中随时都可能存在的噪声。传统单幅图像的超分辨重建算法是从低分辨率图像Y中尽可能准确地估计出高分辨率图像X*。
1.1 高、低分辨率字典的训练
在高、低分辨率字典训练时,本文使用了77 张标准的自然图像作为训练集。部分用以高、低字典对训练的训练图像如图2 所示。

图2 部分训练图像
首先使用的训练图像是不含有噪声的,其中高分辨率图像Ih= {I},与之对应的低分辨率图像Il= {I}。这里值得注意的是,为了提高相邻贴片之间的兼容性,使它们具有相同的图像尺寸,低分辨率图像先进行下采样再插值放大,如公式(2)所示:

其中,H为上采样因子,下采样、插值放大均使用双立方插值。分别对高、低分辨图像{Ih,Il}进行分块处理,图像块大小都是w×w。最终,得到高、低分辨率图像块{ph,pl}。如公式(3)所示。
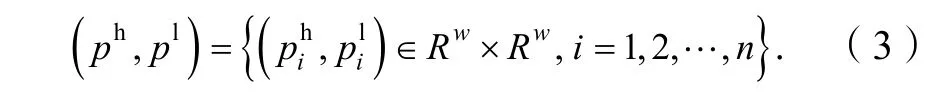
类似于SRCR[9]中的字典设计思路,假设原始高分辨率图像和输入低分辨率图像分别在耦合字典HD和LD上具有相同的稀疏系数。和传统算法不同的是,为了增加对噪声的抗干扰性,参与高分辨率字典HD训练的不仅是高分辨率图像块HP的纹理结构,低分辨率图像块LP的纹理结构也被用来学习。在重建阶段,HD可以用来估计高分辨图像和不含噪声的低分辨图像。LD代表了图像的基本结构,为了提取适当的特征,本文使用简单有效的一阶导数和二阶导数作为滤波函数。用于提取特征的4 个滤波器为
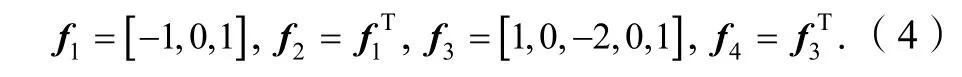
基于上面给出的滤波器,可以提取每个图像块的4 个不同方向的特征。将4 个特征向量拼接成一个向量并作为低分辨率图像块的最终特征表示。
通过上述方法,字典训练数据可以通过以下方式获得:

其中:(pH,pL)是相应的高、低分辨率图像对,是的平均值,是的平均值,F()是由公式(4)提取的特征向量并将4 个特征向量拼接成一个向量。由于高、低分辨率图像块提取特征方式的不同,DH∈RN×S和DL∈RM×S并不是简单的线性连接,其中S是字典中原子的数目。因此通过使用公式(6)来完成字典联合训练的过程。
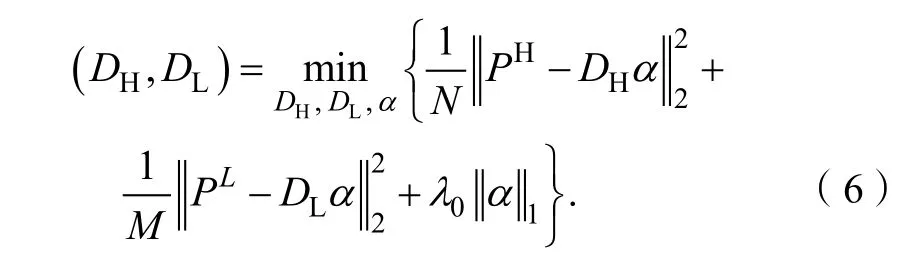
其中N和M是向量形式的高、低分辨率图像贴片的尺寸。在实际训练过程中,可以将上述公式简化为
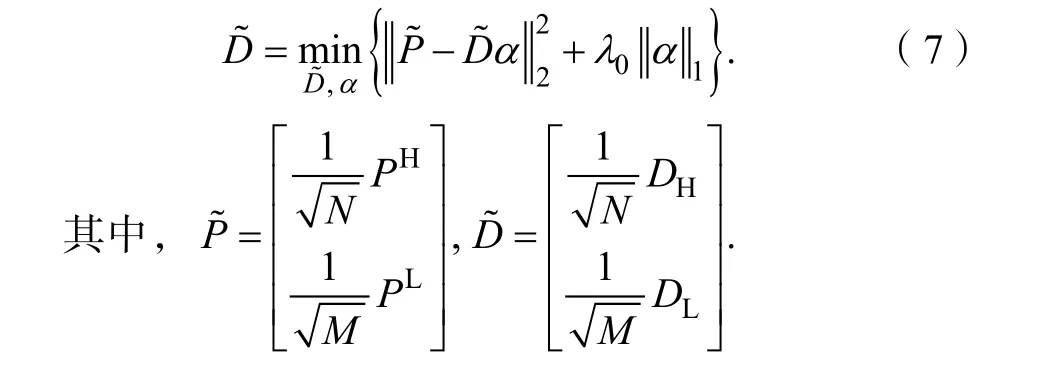
训练的过程是一个典型的稀疏系数求解的过程。然而,求解稀疏模型的过程往往需要花费很多的时间。Zeyde 等[10]通过OMP[14]和PCA[15]节省了字典学习的时间。所以,对于稀疏字典的学习,本文使用Zeyde 等[10]的方法。
1.2 相似块的选取和权重计算
首先,将输入的低分辨率图像LY通过双立方插值放大到和原始高分辨率图像XH相同的尺寸大小。然后将其分割成大小为w×w,数目为N的重叠低分辨率图像补丁。
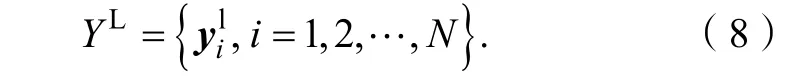
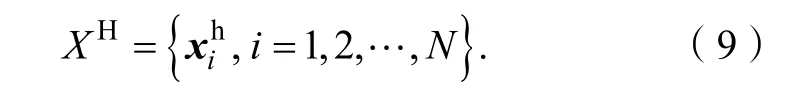

其中Vi是噪声。假设它是均值为零且方差为σ2的高斯噪声,由于局部图像结构具有重复性,可以找到和结构相似的图像补丁集合{},pl},并通过合理的权值分配重建估计的高分辨率图像补丁:

其中,权重向量ωi=[ωi1,ωi2,...,ωik]T,而k是相似图像补丁的数目。
通过上述描述,可以得到如下推导:

其中,Vi是假设的均值为零且方差为σ2的高斯噪声,所以εi和σ2相关。也就是说,在误差可控的范围内,通过输入的低分辨率图像补丁和选取的相似图像补丁可以得到合理的权值分配ωi。因此,重建阶段的关键在于从pl选取和输入图像补丁结构相似的图像补丁集合,并获得合理的权重分配ωi。传统算法通过欧式距离来描述这种相似性。虽然计算方法简单,但是要从庞大的示例库中为每个输入寻找相似的图像补丁,需要花费大量的时间。由于稀疏字典可以使信号的主要成分集中在少许几个原子上,并且基于稀疏编码的超分辨重建算法[10]展示了对噪声良好的鲁棒性。因此,本文选择用稀疏字典代替原始的示例库并从列原子中选取相似的图像补丁集合,即() ∈(Dh,Dl)。

其中:sqrt(.)是开平方操作,sum(A, 1)是矩阵A的按列求和函数,repmat(a,b) 使a和b具有相同的矩阵维数,Dnl和)n是标准化后的低分辨率字典和输入特征向量,F()n可以由Dnl表示:
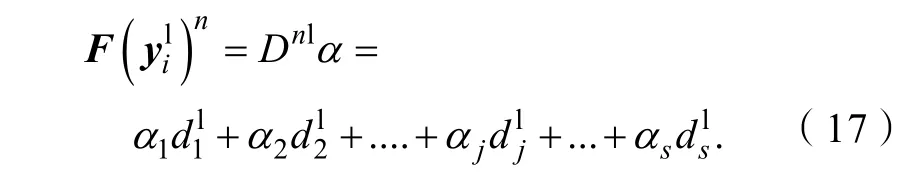
其中:α= [α1,α2, … ,αj, … ,αs],表示低分辨率字典列原子,αj表示和F()n的相关性。其中,α的求解公式如下:
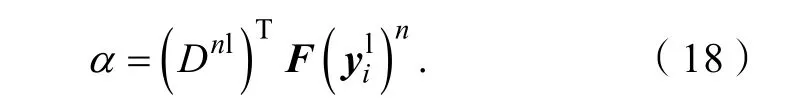
公式(16)和(17)展示了每个字典列原子与输入特征向量之间的相关性。其中,αj越大,和F()n之间的相关性就越强;反之,若αj很小或接近于零,则说明两者之间几乎没有相关性。通过相似性的强弱选择k个相似图像补丁对= 1,2,…,k},
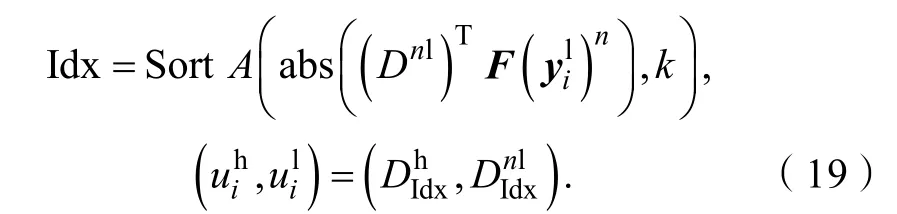
其中:abs(.)是求绝对值操作,S ortA(a,k)是将向量a从大到小排序,并返回前k个的索引值。这样,就从稀疏字典对(Dh,Dnl)中找到了与输入特征相似的k个图像补丁对()。对应的相似度大小βi=[βi1,βi2, … ,βij, … ,βik]计算公式如下:

其中 ,SortB(a,k) 是将向量a从大到小排序,并返回前k个的值。结合公式(15),本文提出了基于L2 范数正则化的最小二乘回归的权值解法:


其中,⋅表示点乘。当相似性很强时,限制项会很小,从而得到较大的权重。相反,当相似性较弱时,限制项会变大,从而获得较小的权重。具体过程如下,先计算每组相似图像补丁之间的差异,即每个相似图像补丁减去每组最相似的图像补丁得到ib,再乘以每个相似图像补丁的相似性iβ,从而得到最终的限制项iC。所以,改进的最小二乘回归模型如下:

其中:λ是正则化参数,ωi是需要求解的权重。通过自适应权值计算模型,ωi会得到合理的权值。这是一个L2范数的约束问题。本文采用0来求解ωi。闭式解表达式如下:


其中:S是线性缩放因子,是线性缩放后的重构向量。根据高分辨率字典的训练方式,不仅包括估计的高分辨率图像补丁还包括去噪后的低分辨率图像补丁。这里值得注意的是,和具有相同的尺度大小。
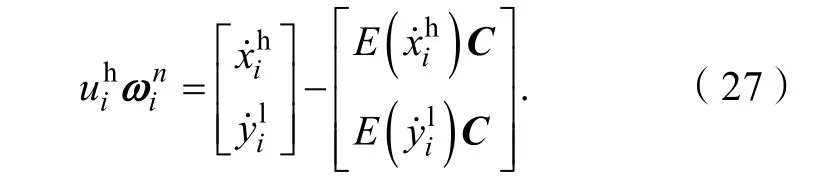
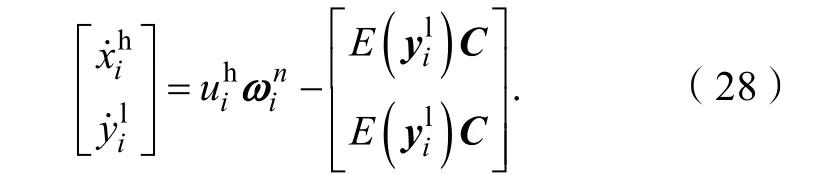

含噪图像的快速超分辨重建算法流程如下:
输入:已训练的联合稀疏字典DH和DL,低分辨率图像YL,相似块数目k,正则化参数λ;
输出:高分辨率图像X*;
初始化:对输入低分辨率图像YL作双立方插值得到与高分辨率图像XH同样大小的低分辨图像,作分块处理得到低分辨率图像块,保证相邻图像块在每个方向均有重叠像素。循环直到处理完所有的图像块:
(2)根据相关性系数α寻找k个相似图像补丁对(),通过公式(20)、(22)计算得到限制项Ci。(3)通过公式(25)计算得到权值分配ωi。
(5)通过重叠区域的加权平均得到高分辨率图像和去噪后的低分辨率图像。
(6)根据和并结合公式(29)得到最终估计的高分辨率图像X*。
2 实验数据和分析
在本节中,将Set5[16]、Set14[16]和B100[17]作为测试图像库。其中,分别包含5、14、100 张用于重建测试的图片。由于人类对光源的变化更加敏感,因此本文算法只在亮度分量通道上执行。首先将图像转换为YcbCr通道,然后将测试算法应用于Y通道。
2.1 主要参数
在本节中,分析算法的主要参数对实验结果的影响。其中包括正则化因子(γ)、字典数目大小、相似图像块个数。
2.1.1 正则化因子
在本文方法中正则化因子γ是一个非常重要的参数。所以,通过实验不同的γ来观察结果并选择最为合适的一个。设置实验基础参数:
(1)放大倍数×2,字典大小为1024 并且k=24;
(2)放大倍数×3,字典大小为1024 并且k=8。
采用Set5[16]作为测试图像库的实验结果如图3 所示。发现曲线并不单调,在γ=0.07时峰值信噪比(PSNR)获得最优值。研究发现,对于不同的测试图像库,正则化因子γ的最优值略有不同。因此,本文建议在实验中设置正则化因子γ=0.07。

图3 正则化因子对PSNR 的影响
2.1.2 字典大小
在实验中,字典大小从64 到2048,并且训练样本都是从训练图像库中训练得到的。设置实验基础参数:
(1)放大倍数×2,γ=0.07并且k=24;
(2)放大倍数×3,γ=0.07并且k=8。
采用Set5[16]作为测试图像库的实验结果如图4 所示。发现字典数目越大,重建质量就越好。同时,也需要更高的计算成本。在图像集Set14[16]和B100[17]中也可以得到类似的结论。为了权衡重建质量和计算成本,接下来实验中字典大小为1024。结果如图4 所示。
2.1.3 相似图像块个数
在相似块的寻找过程中,需要为每个输入图像块寻找相似成分,而相似图像块的个数k会影响该算法的性能。设置实验基础参数:
(1)放大倍数×2,字典大小为1024,γ=0.07;
(2)放大倍数×3,字典大小为1024,γ=0.07。
采用Set5[16]作为测试图像库的实验结果如图5 所示,可以发现在放大倍数×2 的情况下,当k=24时,到达最佳的重建质量。同样,在放大倍数×3 的情况下,k=8。随着k的增大,计算量和内存消耗也会随之增加,重建时间也会明显增加。在图像集Set14[16]和B100[17]中也可以得到类似的结论。所以,经过权衡重构质量和计算时间,在实验中当放大倍数×2 时,设置k=24。当放大倍数×3 时,设置k=8。结果如图5所示。
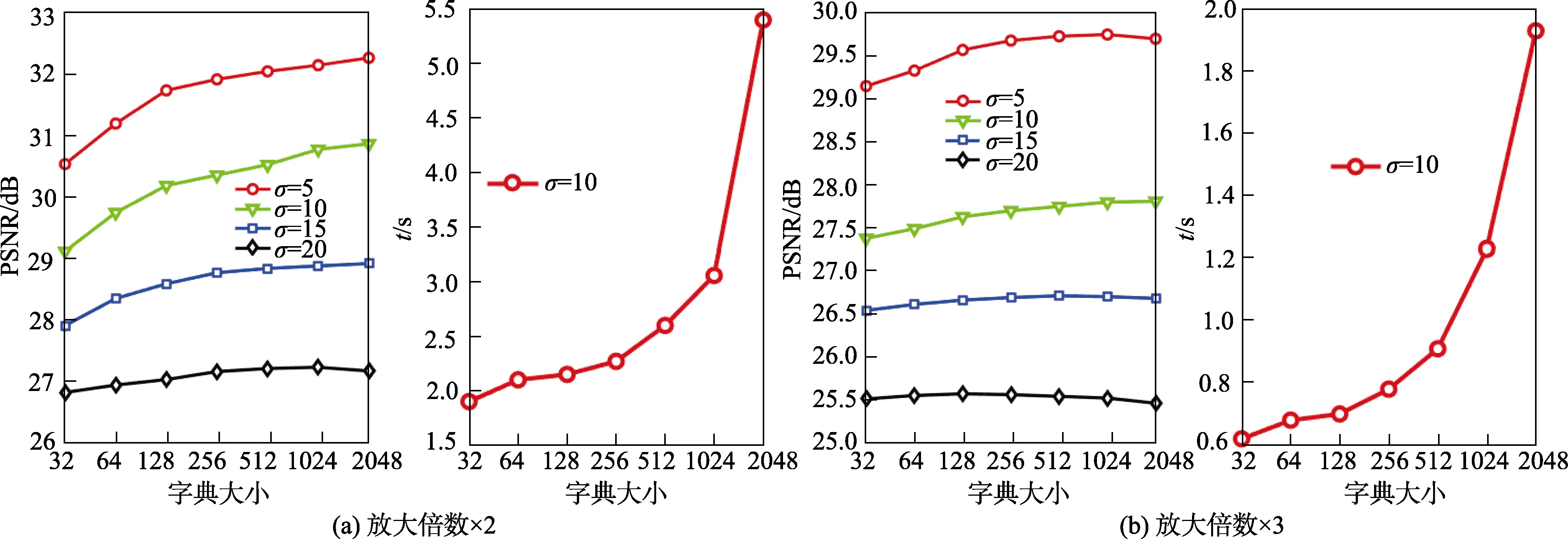
图4 字典大小对性能的影响

图5 相似块个数k 对性能的影响
2.2 性能评估
在本节中,为展示所提算法对噪声图像重建效果的提升,并与NE[6]、Zeyde[10]、A+[16]、SRCNN[17]、CSC[18]算法进行比较,将峰值信噪比(PSNR)和结构相似度(SSIM)作为客观评判指标,并给出了算法的重构时间,比较方法的代码从本文作者的主页下载。试验过程中,使用相同的参数设置,图像块补丁大小为6×6,重叠区域为2,正则化因子γ=0.07,字典大小为1024,放大倍数×2 时,相似块数目k=24,放大倍数×3 和×4 时,相似块数目k=8 。
表1 和表2 列出了PSNR 和SSIM 的比较。当标准差σ=0时,算法CSC[18]表现出了最好的性能,但这和实际应用情况不符。而当σ≠0 时,在图像集Set5[16]、Set14[16]和B100[17]中进行了测试,结果证明本文提出的算法比其他方法更加具有优越性。与CSC[18]相比,当测试集为Set5[16]、放大倍数×2 时,在σ=10时获得最小5.94 dB 的PSNR 提升。在σ=20时,获得最大7.96 dB 的PSNR 提升。同样也优于具有噪声抑制作用的Zeyde[10]算法,在σ=10时,获得最小4.58 dB 的PSNR 提升。在σ=20时,获得最大6.36 dB 的PSNR 提升。当测试集为B100[17],放大倍数×3时,与CSC[18]相比,在σ=10时,获得最小2.39 dB的PSNR 提升。在σ=20时,获得最大5.40 dB 的PSNR 提升。同样也优于Zeyde[10]算法,在σ=10时,获得最小0.64 dB 的PSNR 提升。在σ=20时,获得最大3.81 dB 的PSNR 提升。图6—8 提供了各种方法的重建图像,可以发现本文方法面对噪声图像时,具有更强的鲁棒性从而获得更好的重建效果。
2.3 IBP 的影响
该算法结合迭代反投影(IBP),将去噪后的低分辨率图像用于提高重建高分辨率图像的性能。根据文[20],IBP 可以提高超分辨率重建的效果,但如果输入的是含有噪声的低分辨率图像,IBP 模型会将噪声传播到重建的高分辨率图像。实验结果证明,如果直接输入含噪声的低分辨率图像,IBP 算法性能会变差。结果如表3 所示,设置的迭代次数为20。从表3 可以看出,该方法具有优越性。其他测试数据集Set14[16]和B100[17]也可以获得类似的结果。
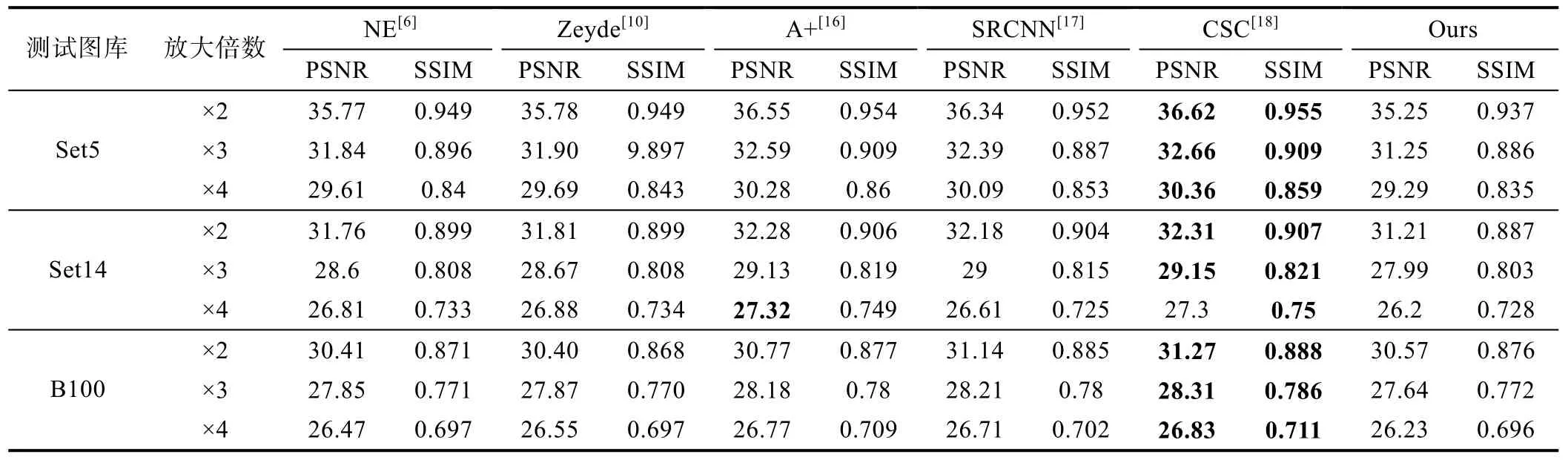
表1 σ=0,PSNR 和SSIM 的比较结果
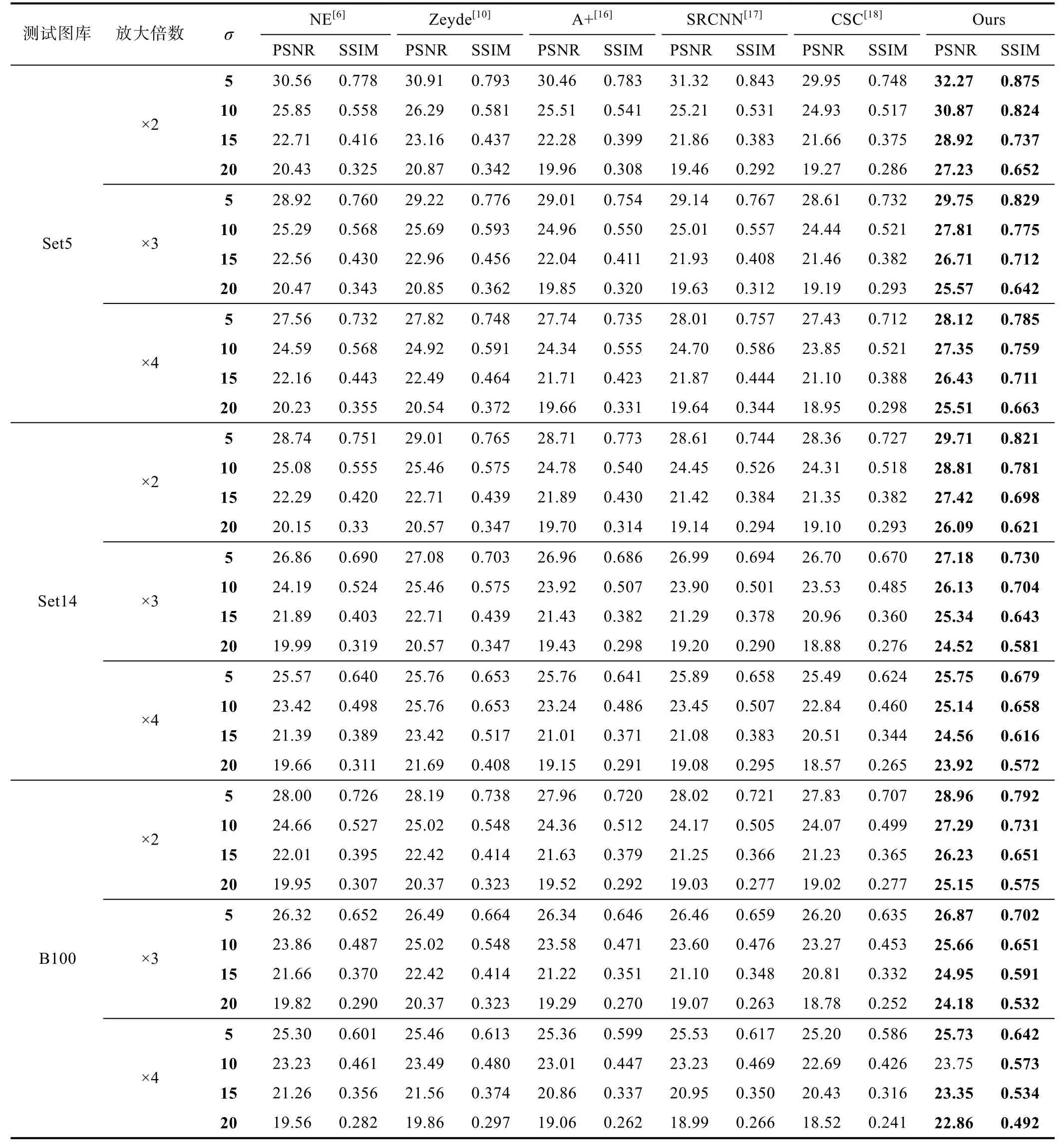
表2 σ ≠0,PSNR 和SSIM 的比较结果

图6 Baby 的各种图像超分辨率方法重建效果对比(放大倍数×2,σ=10)

图7 14037 的各种图像超分辨率方法重建效果对比(放大倍数×3,σ=10)

图8 Face 的各种图像超分辨率方法重建效果对比(放大倍数×3,σ=10)

表3 IBP 对平均PSNR 和SSIM 的影响(Set5)
2.4 距离惩罚效应
采用权重限制模型进行权重的计算。为了验证对改善超分辨率重建性能的效果,在Set5[16]测试数据库上分别执行带权重限制和不带权重限制的方法,并尝试不同的正则化因子γ。结果如图9 所示,由此可见权重限制模型获得了较好的重建效果,其优越性是显而易见的。其他测试数据集Set14[16]和B100[17]也可以获得类似的结果。

图9 距离惩罚对平均PSNR (dB)的影响(Set5)
3 结论与展望
本文提出一种含噪图像的快速超分辨率重建算法,可以很好解决含噪图像的超分辨率问题。在字典训练阶段使用无噪声的示例图像,所以面对不同噪声方差的输入图像,并不需要重新训练字典。在训练的过程中,低分辨率的纹理结构也被用来学习字典,而不是仅仅学习它们的梯度特征。该方法的核心思想在于重建高分辨率图像的同时也重建了输入的低分辨率图像,这将有助于迭代反投影算法[19]进一步提高重建的性能。利用稀疏字典的列原子来计算权值和重构向量,这大大减少了计算时间并通过稀疏表达抑制了噪声。实验结果表明,该方法具有很好的鲁棒性。
