管板流固热耦合分析及优化设计

王天宇，张巨伟，刘哲

工艺与装备

管板流固热耦合分析及优化设计

王天宇，张巨伟，刘哲

( 辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001 )

选用60 mm厚管板流固热耦合模型，计算60 mm厚管箱的3种载荷工况，即单独施加由流固热耦合计算出的温度载荷、单独施加由流固热耦合计算出的压力载荷、同时施加由流固热耦合计算出的温度载荷和压力载荷。并对管板厚度进行改变，做出不同管板厚度下的强度分析，得到当管板厚度为47.5 mm时，为最优化的选择。

管板；温度载荷；压力载荷；强度分析

随着全球能源的日益减少，减耗节能已经越来越得到社会的重视。换热器是实现冷热流体热量交换的通用工艺设备，被广泛的应用于石油化工、钢铁、冶金、节能环保等领域。其中管壳式换热器占据了约70％的换热器市场，所以为了促进管壳式换热器的优化，国内外众多学者已经开展了广泛的研究[1]。张晓彤[2]研究了E43502型换热器在压力载荷、热载荷等共同作用下的应力强度。刘复民[3]研究了重量载荷对管板厚度的影响。本文在对60 mm厚管箱的3种载荷工况进行计算的基础上，改变管板厚度，并探究在不同的管板厚度条件下对最优管板厚度模型计算结果应力最大点进行应力线性化分析，得到最优管板厚度。

1 60 mm厚管板流固热耦合模型

1.1 基本参数

60 mm管板结构参数见表1，固体材料参数见表2，流体材料参数见表3。

表1 结构参数

表2 固体材料参数

表3 流体材料参数

1.2 有限元模型

流体分析采用的是有限体积法，对流体域划分成四面体单元，对于固体域划分成六面体单元。网格扭曲度平均值为0.284 97，最大值为0.895 2。固体域有限元几何模型如图1所示，流体域有限元几何模型如图2所示，固体域有限元网格模型如图3所示，流体域有限元网格模型如图4所示。

图1 固体域有限元几何模型

图2 流体域有限元几何模型

图4 流体域有限元网格模型

1.3 网格无关性测试

为了确保网格划分的合理性，进行了网格无关性测试。合理的网格划分应该能够保证有限元的计算结果不随网格密度的改变而发生明显变化，一般认为加密和减小网格一倍后，计算值的变化量均在5%以内是可以接受的。

表4 网格无关性测试

由表4可知，图3和图4中网格密度己经满足网格无关性要求，网格质量较好，可以排除由网格密度带来的计算误差。

2 边界条件加载

2.1 流体域边界条件

流体域边界条件有进口边界条件，出口边界条件，耦合面。进口边界条件为流速进口，流速为 0.1 m·s-1、进口流体温度为150 ℃。出口边界条件为压力出口，出口压力为2 MPa，进口边界条件如图5所示，出口边界条件如图6所示，耦合边界如图7所示。

图5 流体入口

图6 流体出口

图7 流体域流固耦合面

2.2 固体体域边界条件

固体域边界条件有管箱与空气自然对流换热面，管箱与水强制对流换热面，热流量为零的固体域循环对称接触面，耦合面。管箱与空气自然对流换热面的对流换热系数为10 W/（m2·k），空气温度为22 ℃，如图8所示。管箱与水强制对流换热面的对流换热系数为5 000 W/（m2·k），水的温度为22 ℃，如图9所示。固体域循环对称接触面如图10所示

图8 空气自然对流换热面

图9 与水强制对流换热面

图10 固体域循环对称接触面

图11 固体域流固耦合面

3 流固耦合计算结果

3.1 流体域计算结果

流体域计算结果包括温度云图、压力云图、速度云图。流体域耦合面温度云图如图12所示，固体域耦合面温度云图如图13所示，新建平面如图14所示，新建面上温度分布云如图15所示，耦合面压力分布云图如图16所示，新建平面压力云图如图17所示，速度流线图如图18所示。

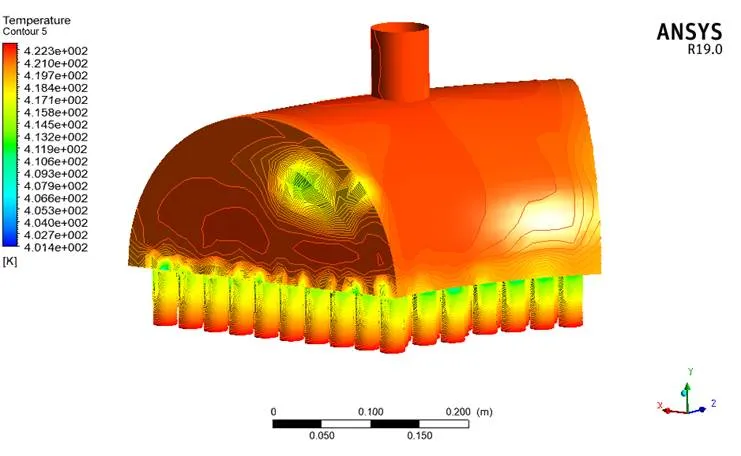
图12 流体域耦合面温度云图

图13 固体域耦合面温度云图

图14 新建平面

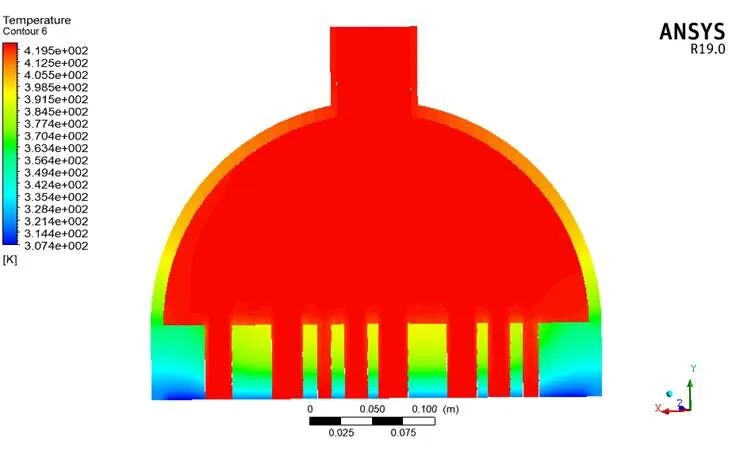
图15 新建面上温度分布云图

图16 耦合面压力分布云图

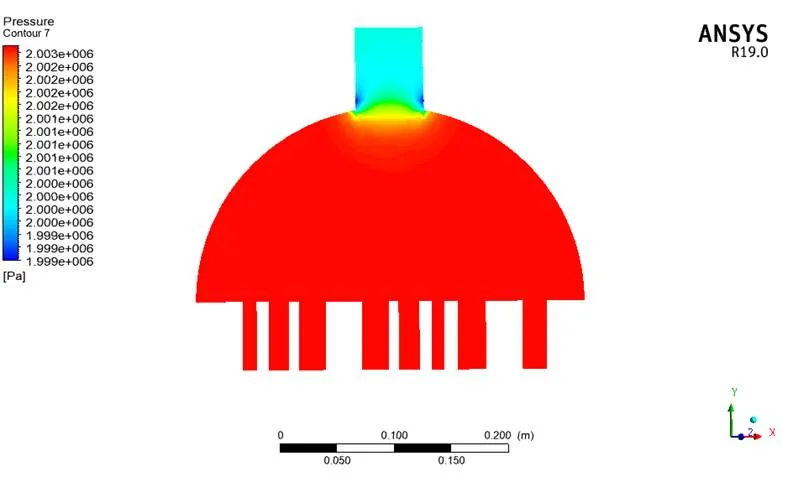
图17 新建平面压力云图

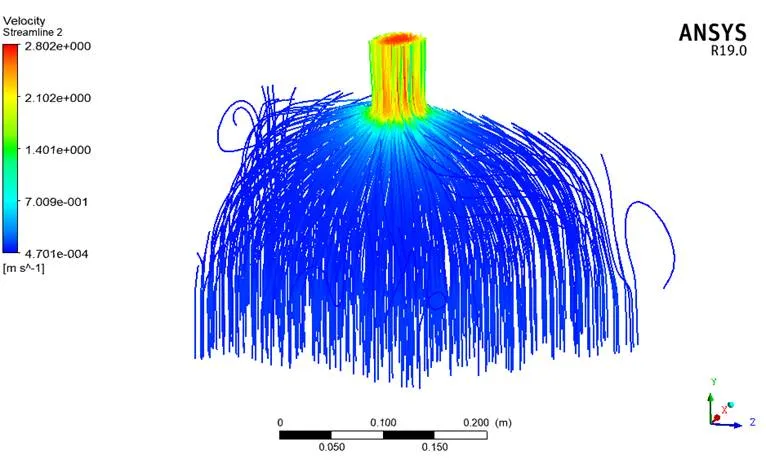
图18 速度流线图

由计算结果可知，管板温差很大，由连续性方程可知流速最大处在出口处。流速大的出口，其压力反而比较小，这是由于流速增加，动压增加所致。其壁面压强变化很小。

3.2 固体域计算结果

固体计算结果可以得到整个管箱的温度分布云图，包括整体管箱分布云图和管板温度云图如图19、图20所示。

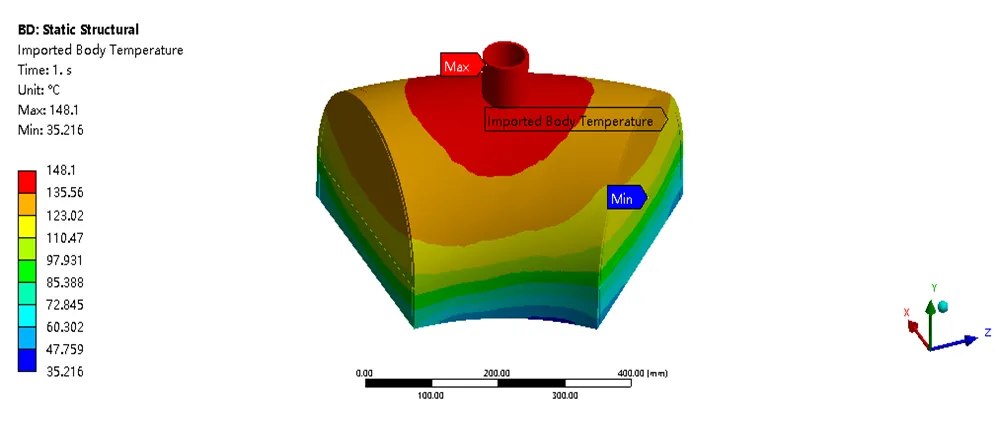
图19 管箱整体温度分布云图

图20 管板温度分布云图

4 结构分析

4.1 网格划分和网格无关性测试

管箱结构分析中，采用solid185实体单元进行网格划分。solid185单元由8个节点定义，每个节点有可沿三个方向平移的3个自由度，此单元支持塑性分析、超弹性分析、应力强化分析、蠕变分析、大挠度和大应变分析等常见分析，同时还能够模拟不可压缩弹塑性材料的变形以及完全不可压缩超弹性材料，solid185单元的结构示意图如图21所示，管箱有限元网格模型如图22所示。

图21 solid186单元示意图

为确保有限元网格模型具有较高的网格质量，本节在进行网格划分过程中对整体几何模型中的不规则结构进行了复杂的切分工作，使几何模型规则化，从而保证几何模型中所有的体素在网格划分过程中都可以采用sweep方式进行划分，管箱有限元网格模型如图22所示，总网格数量约为9.95万个，95%以上的网格均为六面体网格。

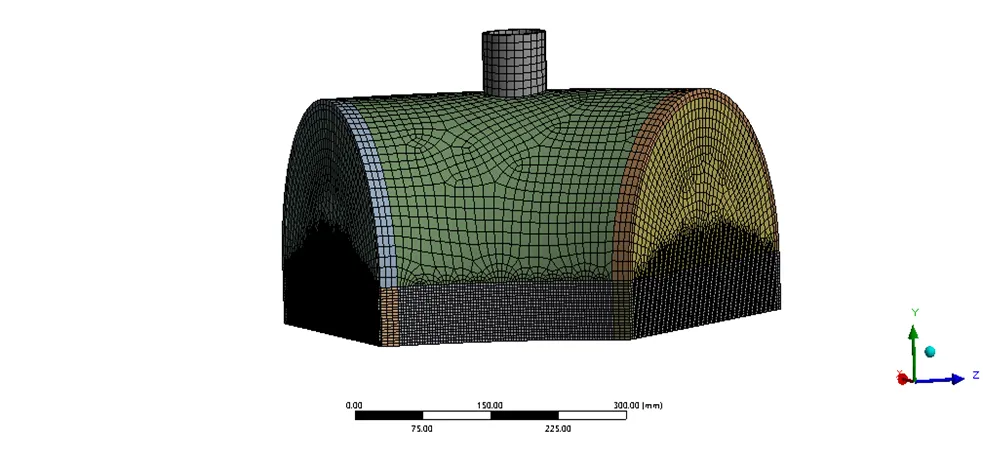
图22 管箱有限元网格模型

为了确保网格划分的合理性，进行了网格无关性测试。合理的网格划分应该能够保证有限元的计算结果不随网格密度的改变而发生明显变化，一般认为加密和减小网格一倍后，计算值的变化量均在5%以内是可以接受的。

表5 网格无关性测试

由表5可知，图22中网格密度己经满足网格无关性要求，网格质量较好，可以排除由网格密度带来的计算误差。

4.2 载荷和约束

由Fluent计算出来的温度场和压力场施加到结构计算当中，其约束为无摩擦约束，如图23所示。

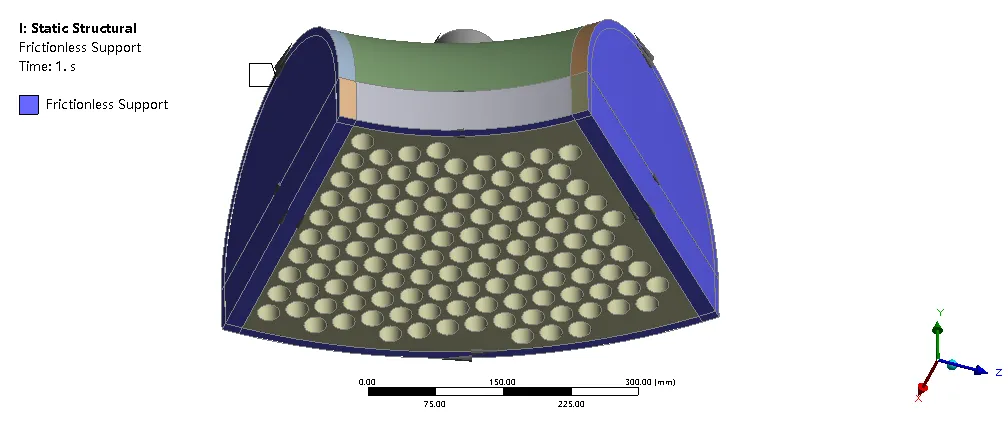
图23 约束示意图

4.3 分析结果与强度校核

按照JB 4732—1995《钢制压力容器—分析设计标准》的规定，强度校核采用最大剪应力理论，应力强度规定为最大剪应力的二倍，即：

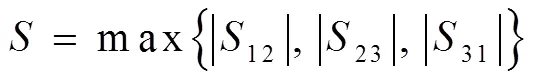
式中：12=1-2，23=2-3，31=3-1，—应力强度；

1、2、3—主应力。

一次总体薄膜应力强度Ⅰ应不超过设计应力强度值m，即：

Ⅰ≤m。

一次局部薄膜应力强度Ⅱ许用值为1.5m，即：

Ⅱ≤1.5m。

一次局部薄膜应力加一次弯曲应力的应力强度Ⅲ的许用值为1.5m，即：

Ⅲ≤1.5m。

一次局部薄膜应力加一次弯曲应力以及二次应力的应力强度Ⅳ的许用值为3m，即：

Ⅳ≤3m。

一次局部应力加二次应力以及峰值应力的应力强度Ⅴ的许用值为a，即：

Ⅴ≤a。

式中：—载荷组合系数，对于本分析，=1；

m—材料在设计温度下的设计应力强度；

a—材料在一定循环次数下的疲劳许用应力强度值。

为求取应力强度值，应根据有限元计算结果，在构件不同部位，过危险应力点沿厚度做路径，进行应力线性化处理，得到膜应力强度及膜加弯应力强度。对于模型中部分结构，当其最大应力强度值小于一倍的许用应力强度时，不在结构中做应力线性化并进行应力分类，而将最大应力强度值按照一倍许用应力强度进行校核。

若结构最大应力强度值小于一倍的许用应力强度，不必给出应力线性化路径，如图24至图26所示。材料的许用应力见表6。为保守起见，取173 MPa为材料的强度校核许用值。

表6 材料的许用应力

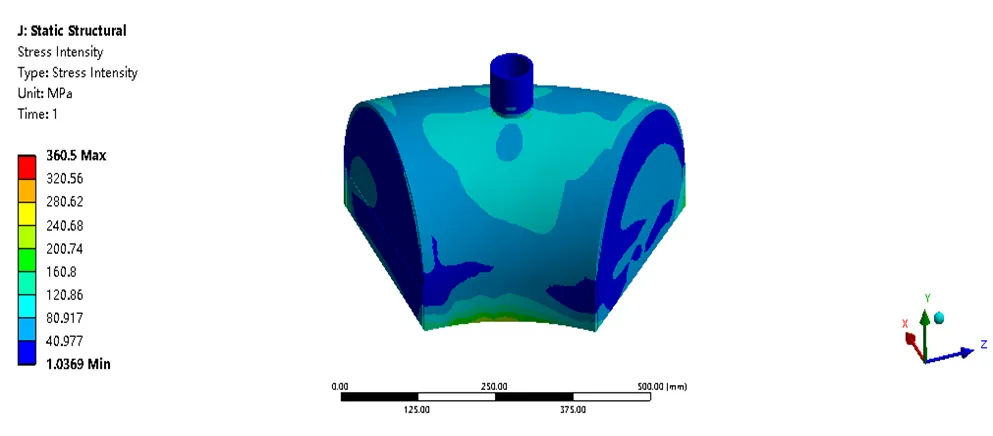
图24 整体结构应力强度分布（MPa）

图25 半圆板应力强度分布（MPa）

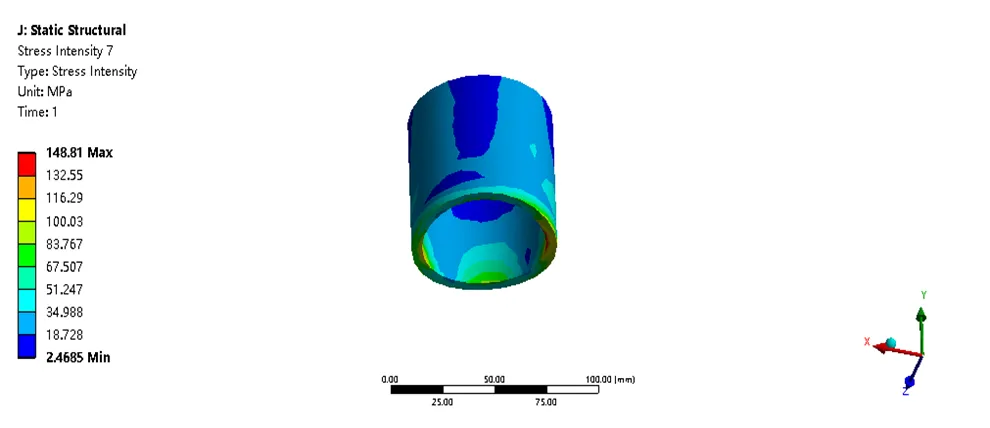
图26 接管应力强度分布（MPa）

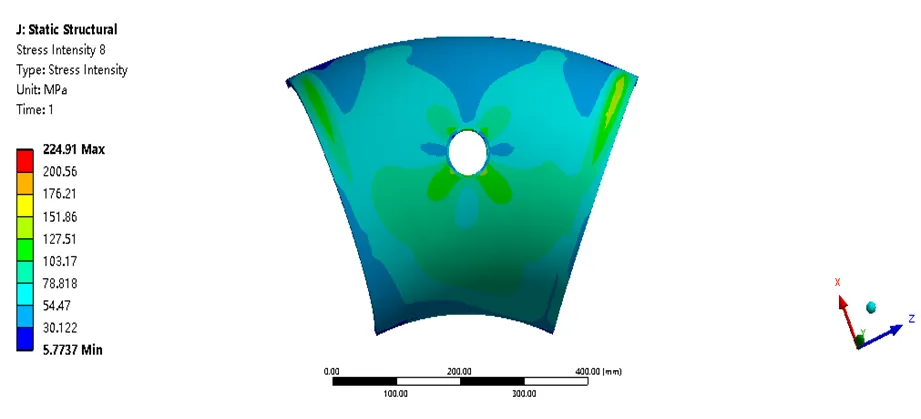
图27 环形半圆柱体应力强度分布（MPa）

图28 环形半圆柱体路径示意图

表7 环形半圆柱体应力评定结果

图29 管板应力强度分布（MPa）

图30 管板路径示意图

表8 管板应力评定结果

5 管板优化设计

5.1 三种载荷工况管箱分析结果

计算60 mm厚管箱的三种载荷工况，即单独施加由流固热耦合计算出的温度载荷、单独施加由流固热耦合计算出的压力载荷、同时施加由流固热耦合计算出的温度载荷和压力载荷。其压力云图如图31至图33所示。由云图可知，只加温度载荷最大应力为358.23 MPa，只加压力载荷最大应力为27.038 MPa，温度载荷与压力载荷共同作用最大应力为360.5 MPa。温度载荷占据主导作用。

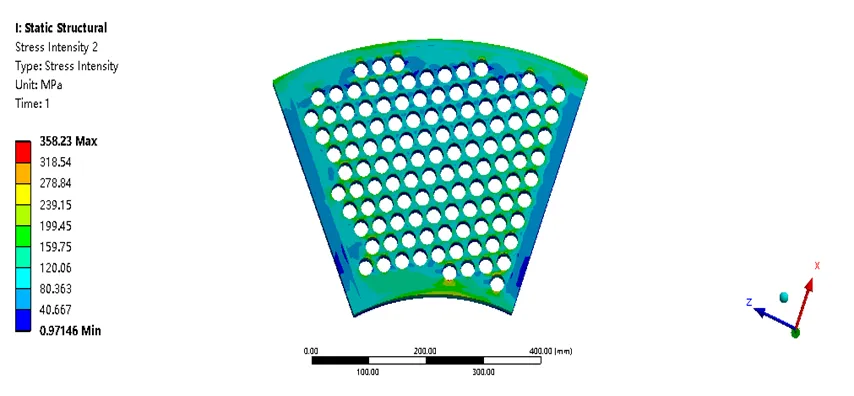
图31 只施加温度载荷管板应力强度分布（MPa）

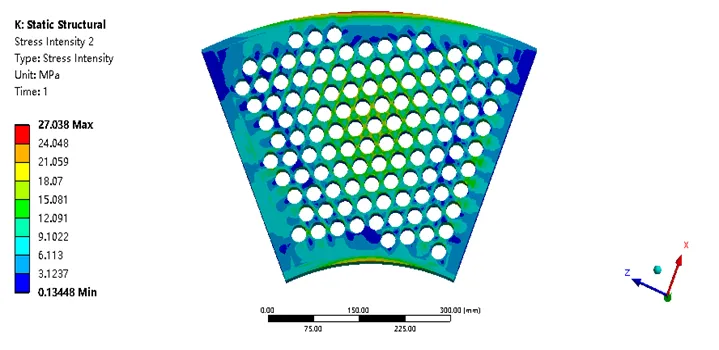
图32 只施加压力载荷管板应力强度分布（MPa）

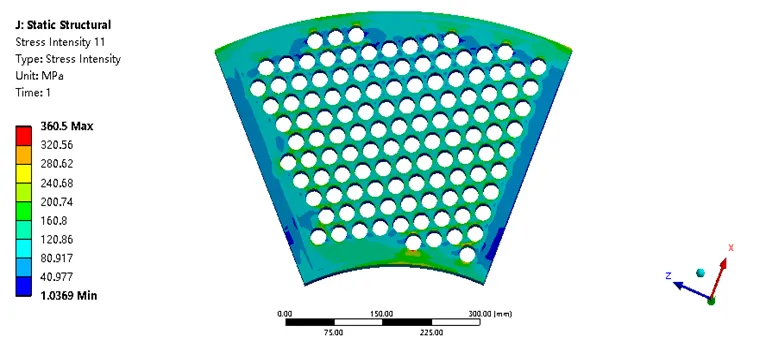
图33 施加压力和温度载荷管板应力强度分布（MPa）

5.2 不同厚度管板流热固分析

对不同厚度管板进行流热固分析，其计算结果见表9。表9中数据为，只加温度载荷记录其最大温差应力，施加温度载荷与压力载荷记录其最大总应力，并对数据进行处理，其中随管板厚度变化管板管程侧温度变化曲线如图34所示，随管板厚度变化管板壳程侧温度变化曲线如图35所示，随管板厚度变化管板内外温度差变化曲线如图36所示，随管板厚度变化温差应力变化曲线如图37所示，随管板厚度变化总应力变化曲线如图38所示，总应力与温差应力差变化曲线如图39所示。

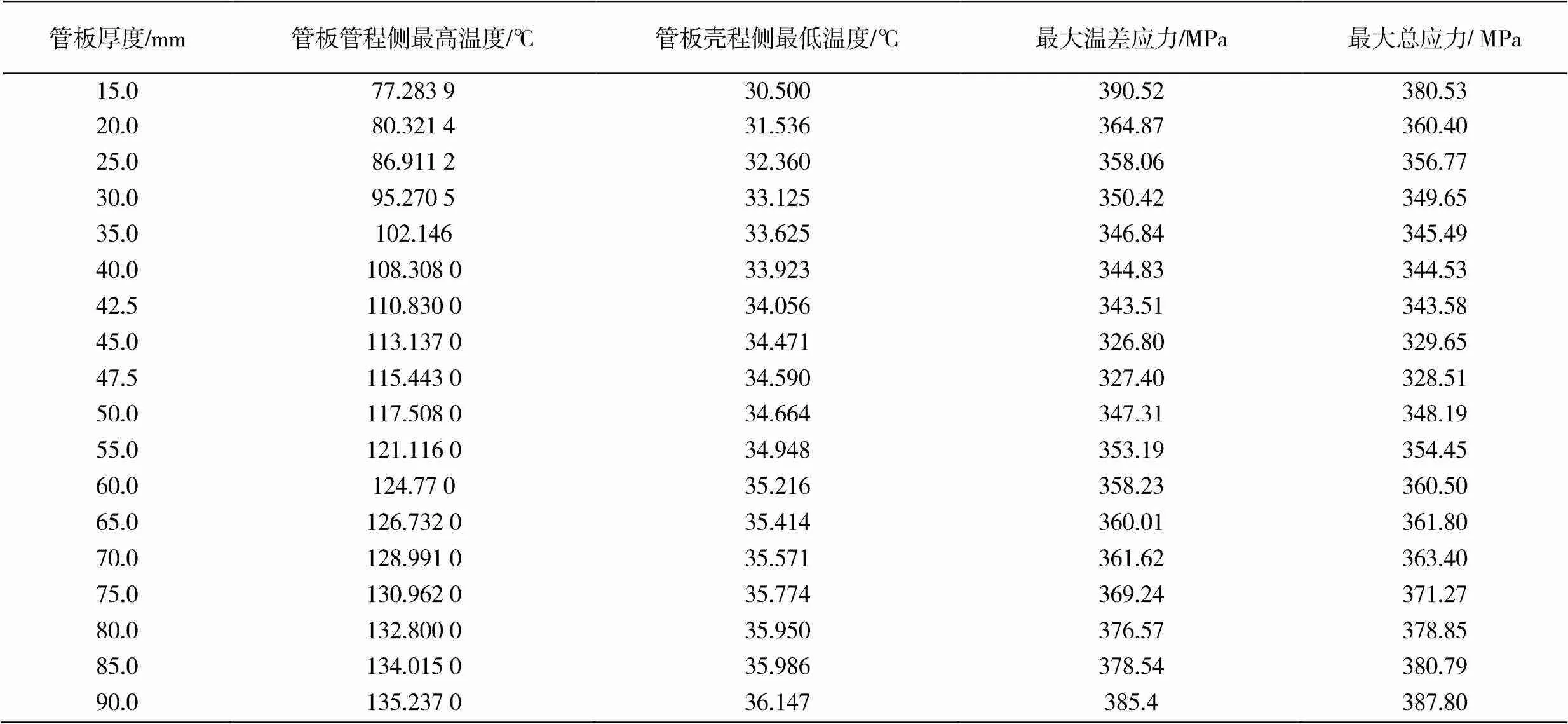
表9 不同厚度管板计算结果

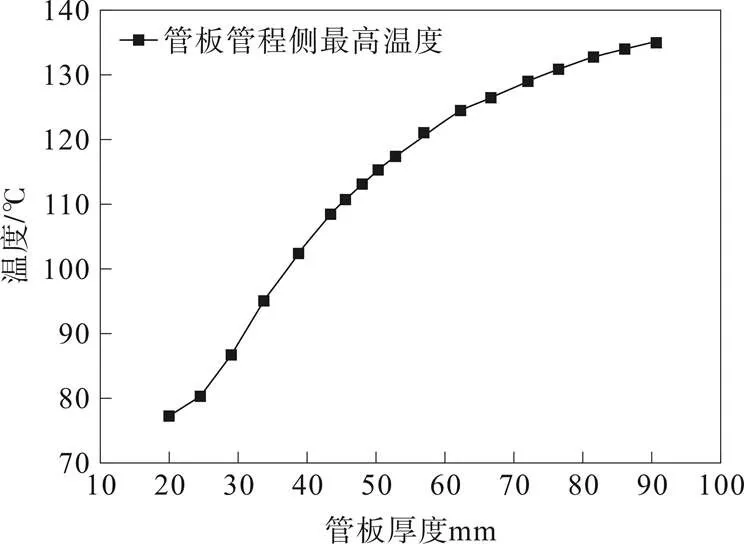
图34 随管板厚度变化管板管程侧温度变化曲线

图35 随管板厚度变化管板壳程侧温度变化曲线

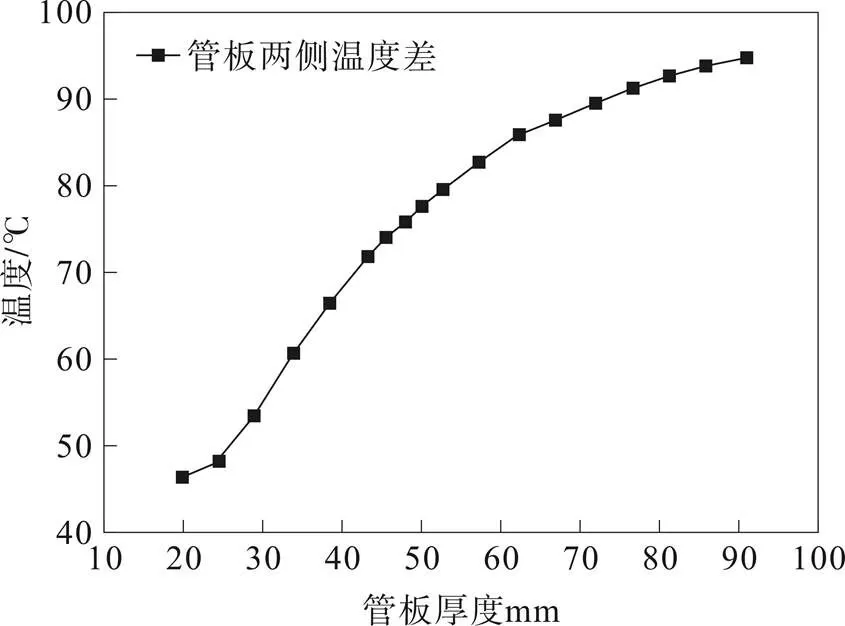
图36 随管板厚度变化管板内外温度差变化曲线

图37 随管板厚度变化温差应力变化曲线

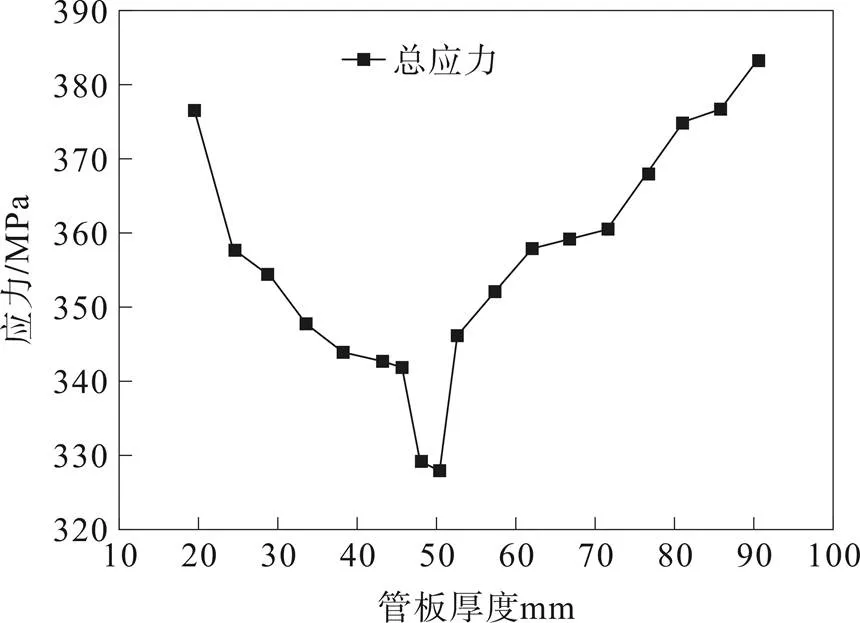
图38 随管板厚度变化总应力变化曲线

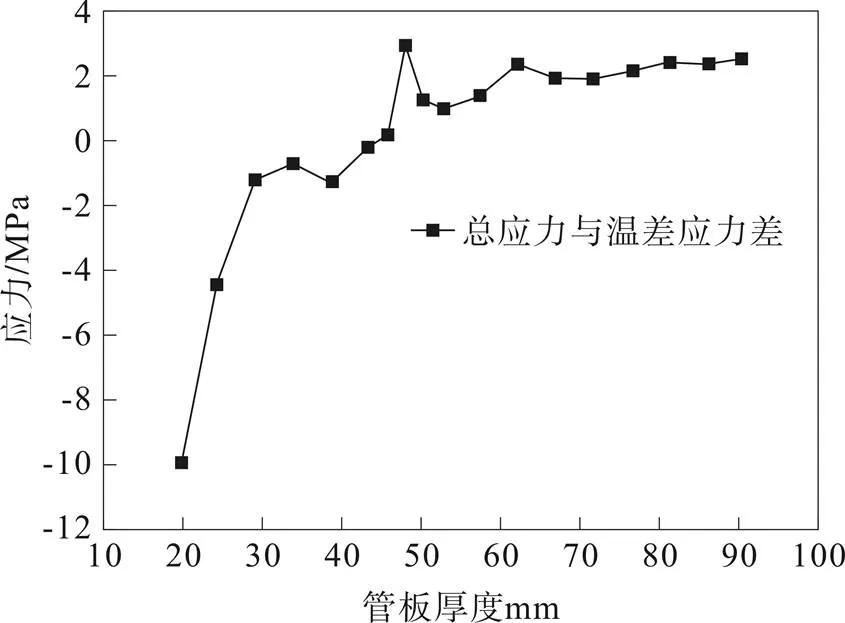
图39 总应力与温差应力差变化曲线

管板壳程侧温度随管板厚度增加而增大，管板管程侧温度随管板厚度增加而增大，管板两侧温差随管板厚度增加而增大。由于管板比较薄的时候热阻小热通量大，管程侧管板接触流体温度低，管程侧管板温度较低，壳程侧管板温度也较低。随着管板厚度增加管板热阻增大，热通量减小，管程侧管板接触流体温度升高，管程侧管板温度升高，壳程侧管板温度也升高。

随管板厚度增加温差应力先减小后增加，总应力同样是先减小后增加，总应力与温差应力差值逐渐增大。随着管板厚度增加局部温度梯度减小，温差应力和总应力水平降低，管板继续增厚，由于温差导致的上下表面之间变形协调更难，导致互相约束更强，温差应力与总应力增加。故管板厚度不应该盲目增加，其热应力会随着管板厚度增加先减小后增加。

6 最优方案与初始方案对比

6.1 优化后的管箱应力强度分析

在边界条件不变的情况下由管板优化分析的结果表明最优管板厚度为47.5 mm。同样计算47.5 mm厚管箱三种载荷工况，即单独施加由流固热耦合计算出的温度载荷、单独施加由流固热耦合计算出的压力载荷、同时施加由流固热耦合计算出的温度载荷和压力载荷，其应力云图如图40至图42所示。

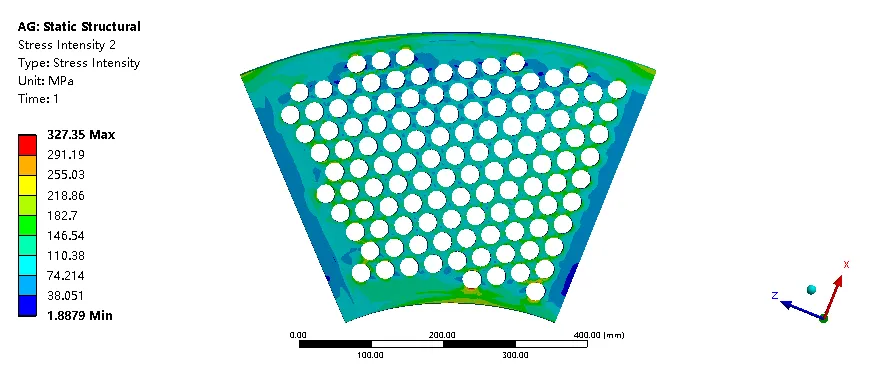
图40 只施加温度载荷管板应力强度分布（MPa）

图41 只施加压力载荷管板应力强度分布（MPa）

图42 施加压力和温度载荷管板应力强度分布（MPa）

图43 管板路径示意图

6.2 优化前后对比分析

表10 管板应力评定结果

对厚度为47.5 mm和50 mm的管板进行对比，对比结果见表11。

表11 优化前后对比

由表11可知，优化后主要是降低了峰值应力，结构抵抗疲劳载荷的能力增加。

7 结 论

随着管板厚度增加管板内外温差增加，管程侧最高温度有明显的增加，壳程侧最低温度也相应增加。其温差应力会随着管板厚度增加有明显的先下降后增加的变化。对最优管板厚度模型计算结果应力最大点进行应力线性化分析可以发现，主要是降低了该点的峰值应力。峰值应力不引起结构显著的变形，它是一种可能导致疲劳裂纹或脆性断裂的原因。管板厚度为47.5 mm时，为最优化的选择，优化后主要是降低了峰值应力，大大增加了结构的疲劳寿命。

[1] 马晓驰.国内外新型高效换热器[J].化工进展，2001，20（1）：49-51.

[2] 张晓彤，吴世春，杨任，等.E43502型换热器管板的有限元强度校核[J].冶金能源，2019，38（3）：18-21.

[3] 刘复民.重量载荷对立式换热器管板的影响[J].大氮肥，2019，42（3）：155-158.

[4] 陈杰，纪博文，庄大伟，等.绕管式换热器管板的有限元应力分析与结构优化[J].化工学报，2018，69（S2）：128-134.

[5] 严翔. 承压条件下管板局部应力对比分析[D].武汉：武汉工程大学，2018.

[6] 古丽娜尔·图尔逊，哈尼帕·哈不都拉，阿尔孜古力·巴亚合买题.固定管板换热器关键结构的计算机模拟研究[J].江西化工，2018 （1）：42-46.

[7] 杨良瑾，桑如苞，杨旭.管壳式换热器管板的疲劳分析设计方法探讨[J].石油化工设计，2017，34（4）：1-5.

[8] 颜云辉，谢里阳，韩清凯.结构分析中的有限单元法及其应用[M].沈阳：东北大学出版社，2008.

[9] 印铁，苏世明，王强.有限单元法在结构优化设计中应用[J].光电技术应用，2003（3）：44-47.

[10] 侯静.基于ANSYS的加氢反应器的结构优化设计及可靠性分析[D].新疆：新疆大学，2007.

[11] 陈笑梅.浅谈ANSYS软件在工程中的应用[J].科技创新导报，2006（14）：162-163.

[12] 栾春远.压力容器ANSYS分析与强度计算[M].北京：中国水利水电出版社，2008.

[13] 张艳春，于国杰.压力容器分析设计及其在工程中的应用[A].左其华，窦希萍.第十五届中国海洋（岸）工程学术讨论会论文集[C].江苏：海洋出版社，2011.

[14] THOMAS D. Metallurgical analysis to evaluate cracking in a 316L grade stainless steel spiral heat exchanger[J].,2012,2：198-203.

[15] MA T ,CHEN Y T . Stress analysis of internally finned bayonet tube in a high temperature heat exchanger[J]., 2012, 43:101-108

Fluid-Solid-Heat Coupling Analysis and Optimization Design of Tube-Sheet

,,

（College of Mechanical Engineering , Liaoning Shihua University, Fushun Liaoning 113001, China）

The fluid-solid-thermal coupling model of tube sheet with 60 mm thick was selected to calculate the three load conditions of 60 mm thick tube box, namely, the temperature load calculated by the fluid-solid thermal coupling was applied separately, the pressure calculated by the fluid-solid thermal coupling was separately applied,and the temperature load and pressure load calculated by fluid-solid-heat coupling were applied at the same time. The thickness of the tube sheet was changed, and the strength analysis under different tube sheet thicknesses was carried out. The results showed that optimal tube sheet thickness was 47.5 mm.

Tube sheet; Temperature load; Pressure load; Strength analysis

2020-04-24

王天宇（1994-），男，辽宁省抚顺市人，硕士， 2020年毕业于辽宁石油化工大学化工机械专业，研究方向：石油化工设备及安全。

张巨伟（1962-），男，教授，硕士，研究方向：安全工程、振动理念及应用。

TK123

A

1004-0935（2020）09-1081-08