微型低温节流制冷器结构优化设计

曹 菁，侯 予，李家鹏，陈 军，陈双涛，陈 良

〈制冷技术〉

微型低温节流制冷器结构优化设计

曹 菁1，侯 予1，李家鹏2，陈 军2，陈双涛1，陈 良1

（1. 西安交通大学能源与动力工程学院，陕西 西安 710049；2. 昆明物理研究所，云南 昆明 650223）

J-T节流制冷器被广泛应用于多种红外设备中。在有限结构内达到冷量最大化，是节流制冷器在小型化发展中面临的问题之一。本文在考虑流体物性变化和部件漏热的基础上，建立了一维稳态节流制冷器热力模型，着重对用于节流制冷器的双螺旋翅片换热器中3项结构参数（翅片的肋高、肋厚和肋间距）对换热器性能的影响进行了计算分析，并采用遗传算法对结构参数进行了优化。研究结果表明：论文所进行的数值计算与实验结果吻合较好；在给定工况和结构参数范围内，肋高和肋厚增加会导致换热器的熵产和冷端冷量都增加、肋间距增加则使换热器的熵产和冷端冷量都减少；并存在最优参数使换热器冷端冷量最大。本文所建立的计算方法为J-T节流制冷器在工程应用中的结构优化和设计提供了高效的途径。

J-T制冷器；翅片换热器；数值模拟；结构优化

0 引言

微型节流制冷器是一种广泛用于红外探测、热成像技术和冷冻手术刀等设备的制冷设备，以其结构紧凑、启动迅速、无振动、可靠性高等优点，成为低温医学、低温电子学和国防等领域的关键技术[1]。作为红外寻的系统的辅助设备，微型节流制冷器的工作性能和结构参数都受到严格限制。在有限结构内为红外芯片的工作环境实现冷量最大化，是节流制冷器在小型化发展中面临的问题之一。

进行节流制冷器流动换热机理的研究是实现其性能优化的基础。早在1994年，Maytal等人[2]将节流制冷器简化为一个理想化数值模型，根据理想气体方程以及压降和热负荷对制冷器的运行特性进行了简单的理论分析。随后，Chou[3]、Xue[4]和Ng[5]等人先后对Hampson型节流制冷器进行了以氮气和氩气作为制冷工质的实验研究和理论分析，提出了基于气体物性参数变化的一维节流制冷器数值模型。Hui等人[6]分析了流体在微小通道中的节流作用，对前人提出的数值模型进行了修正和发展。Hong等人[7]对考虑了气库的节流制冷器模型进行了理论分析，并预测了气库容积和初始压力对制冷器性能的影响。

已有的研究中，除了对已知结构的节流制冷器进行更加详细的基础理论研究之外，也在节流制冷器的结构优化方面进行了有益的尝试和探索。Lerou等人[8]采用最小熵增法对微通道节流制冷器中通道的长、宽、高3项基本参数进行优化计算，并对净冷量、压缩机等效能耗等性能进行分析。Gupta等人[9]对换热器中翅片与间壁间隙大小对回热器性能的影响做了分析比较，对换热器的几何参数进行了单因素性能影响分析。Liu等人[10]采用响应面优化法，研究了最小可用能损失的换热器结构优化，得到了限定工况下的最优结构配置，实现了换热器的性能最佳。

从上述文献中可知，研究者对节流制冷器的优化主要着重于换热器的几何结构优化，而且是基于特定工况下的最优结果，缺乏该最优结构用于节流制冷器系统的验证过程。对于优化后的最优结构对节流制冷器整个工作过程的影响和性能的分析，并没有相关的研究和深入。本文在考虑流体实际物性、各部件漏热以及双螺旋换热器的复杂结构的基础上，建立了一维稳态节流制冷器热力学计算模型，综合分析了节流制冷器中换热器的翅片参数和其他结构参数对换热器性能的影响。以换热器的最小熵增和最大冷端冷量为优化目标，采用遗传算法对换热器的结构进行了优化。实现了在确定工况下，对换热器几何结构参数的快速设计。最终将得到的最优结构装载到节流制冷器系统模型中，验证了该最优参数对制冷器降温时间和工作时长的影响。

1 数学模型

Hampson型换热器作为节流制冷器中的主要部件，其结构参数对制冷器的性能有至关重要的影响。本文中研究的换热器主要由翅片毛细盘管、芯轴和外壳部分组成，基本结构如图1所示。高压高温流体通过入口进入换热器毛细管内，在流动过程中被外侧回流的低温低压流体预冷，流出换热器的高压高温流体经过节流元件的节流作用，变为低温低压流体；节流后的流体吸收蒸发腔内的热量，通过芯轴和外壳间的环形通道排出。

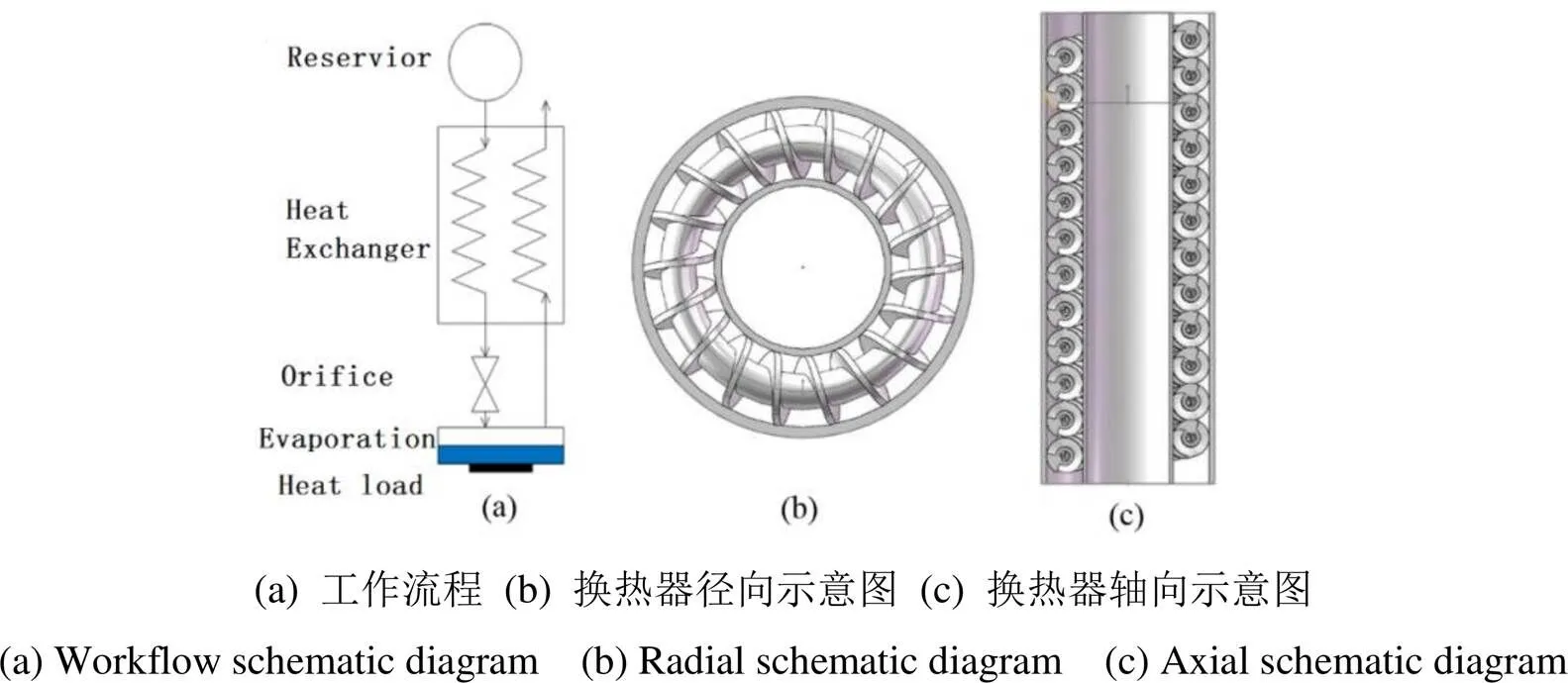
图1 节流制冷器示意图

在进行数值计算时，采用有限体积法划分网格，螺旋翅片管的网格与高压流体的网格划分方法一致，芯轴和外壳的网格与低压流体的网格划分方法一致。具体的网格设定、模型简化以及边界条件参照文献[10]。待求解微元的基本控制方程为：

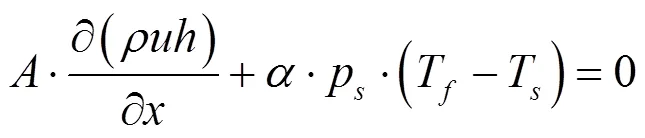
式中：为质量流量，g·s－1；为空间步长，m；为流体密度，kg·m－3；为流体流速，m·s－1；为流体压力，Pa；τ为壁面剪切应力，kg·m－1·s－2；p为湿周，m；为管道通流面积，m2；为流体焓值，J·kg－1；为对流换热系数，W·m－2·K－1；T为流体温度，K；T为固体温度，K；为固体导热系数，W·m－1·K－1；A为固体导热截面积，m2；rad为单位长度辐射传热量，J·m－1。

公式(1)～(3)分别为流体的连续性方程、动量方程和能量方程，公式(4)为固体的能量方程。公式(1)～(4)中的摩擦因子和换热系数相关关联式参照由Timmerhaus等人总结的经验公式[11]。

2 优化算法确定

节流制冷器的结构优化问题，即为数学函数求解最优值问题。对于本文中的结构优化设计，是致力于分析换热器中所有几何参数变化时对换热器性能甚至制冷器性能的影响，且这些几何参数间对最终的结果影响作用复杂，因此本文中将各几何因素对性能的影响假设为目标函数，通过对此目标函数求解最优值来确定最优的几何结构。考虑到遗传算法全局搜索能量强，能够很好地处理约束、跳出局部最优，得到全局的最优解，本文选择遗传算法作为结构设计优化方法。

3 结构优化设计

3.1 模型验证

以文献[5]中的制冷工质和运行工况为例，结构参数参照表1中的基础尺寸。本文中所建立的数值模型求解结果与实验数据的对比见表2。从表中的质量流量和出口温度两项参数的对比中可知，对于不同的进气工况，质量流量的计算误差在±8%以内，冷流体出口处的温度差值在±3K以内。计算模型得到的参数与实验结果的吻合性较好，也表明了此模型的预测结果可以作为后续分析的依据。

3.2 单因素性能影响分析

Hampson型的双螺旋盘管换热器作为节流制冷器中的关键部件，换热器的双螺旋结构主要为翅片螺旋缠绕于毛细管以及带翅片毛细管螺旋缠绕于芯轴。这种双螺旋的结构，既增加了回流冷流体与固体壁面间的接触面积，也使冷流体回流过程更加复杂，加强了冷流体回流过程中的扰动。从表1中基础参数数据的可知，换热器的几何结构参数主要为翅片参数和螺旋参数，为了分析换热器中结构参数对换热器性能的影响，现以表1中的第二栏几何参数基础值作为基准上下浮动，具体参数上下限参数见表1中所示。

在对换热器结构进行单因素影响分析时，假定换热器芯轴的尺寸为固定值，其余参数受到所选单因素参数的影响。对换热器冷端的条件设定为冷流体入口为饱和气态，换热器冷端的冷量为冷端冷流体入口能量与热流体的出口能量之差。图2为换热器中的单因素几何结构对换热器冷端冷量、熵产、冷端入口压力和入口温度的影响。从图中可以看出，各单因素参数的变化对换热器的熵产、冷端入口温度影响并不显著。螺旋圈数（即毛细管长度）、螺旋直径、翅厚和翅高增加时，换热器冷端的冷量都随之增加，但翅间距增加导致换热器冷端冷量的减少。各参数变化时，对换热器冷端入口压力的影响比较显著。螺旋圈数（即毛细管长度）、翅厚增加，冷端入口压力呈现明显增加趋势。在相同质量流量下，毛细管长度的增加增大了冷流体的回流流程，而翅片厚度的增加则加大了冷流体流动的阻力，这两者作用的结果就是冷流体侧入口压力增加，这也导致了冷端温度的升高。翅高和螺旋直径增加，换热器冷端入口压力降低，同时，冷端入口温度减小，这有利于实现换热器在冷端温度较低时满足较大的冷量需求。翅片节距的增加，导致换热器冷端冷量、进气压力急剧下降。以上所有参数中，螺旋圈数与翅厚对换热器的影响变化规律和螺旋直径与翅高对换热器的影响变化规律比较类似。因此本文中以翅片参数（翅片高度、翅片节距、翅片厚度）为例进行优化，并对最优结构进行系统的校核和验证。

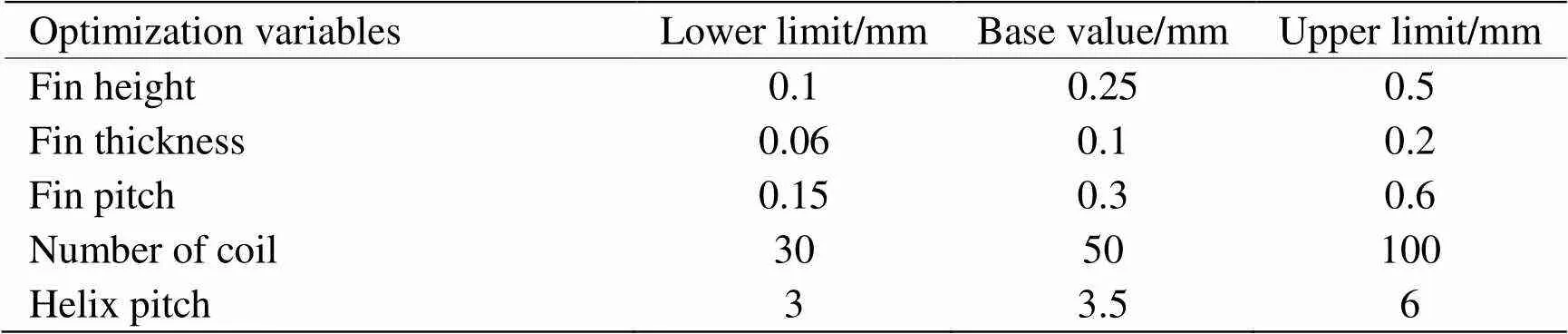
表1 单因素分析参数表

表2 模拟结果与文献中实验数据对比

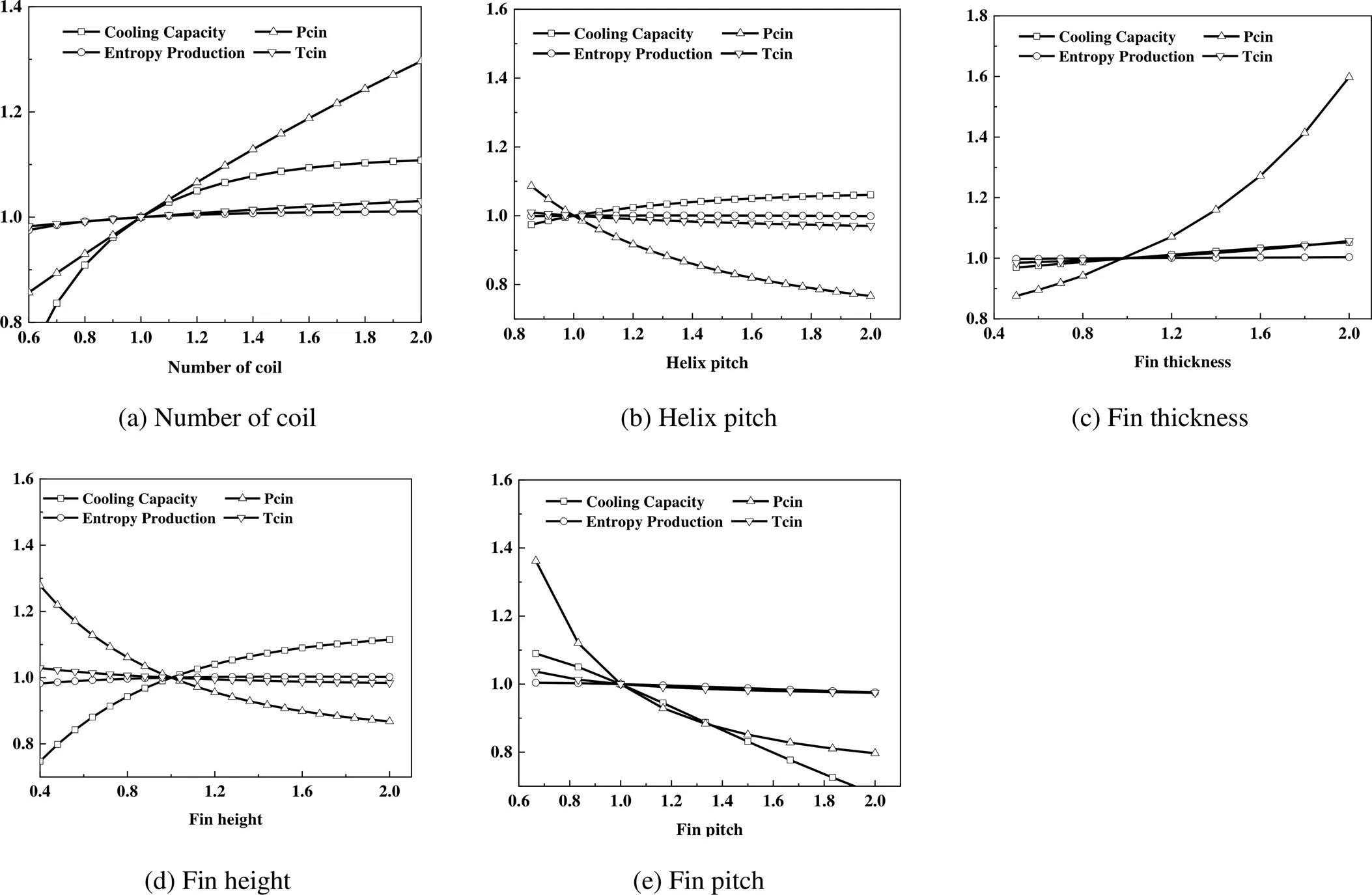
图2 单因素几何参数对换热器性能的影响

3.3 换热器最优结构

根据前文所述，翅片参数的待求解区域分别是：翅片高度为0.1～0.5mm、翅片厚度为0.1～0.6mm、翅片节距为0.1～0.6mm。制冷工质为氩气，换热器的进气端工况为：进气压力18MPa、进气温度300K。流量设定为0.3～0.6g/s。以换热器的熵产最小和冷端冷量最大为优化目标，得到各个工况下的最优结构如表3中所示。从表中结果可知，当进气工况和流量确定时，换热器冷端冷量最大值和系统的熵产最小值出现在翅片厚度最小值和翅片高度最大值。对比不同质量流量的工况，可以发现，翅片节距基本为翅片厚度的2倍左右。因此，在进行换热器的结构设计时，对于肋片参数可以将翅片节距设定为翅片厚度的2倍，以达到较好的换热效果。

3.4 最优结构校核

从换热器中流出的高压流体，经过节流装置的等焓节流过程成为低温低压流体。节流制冷器中采用的节流孔结构与制冷器系统的质量流量可以通过公式(5)确定。根据节流前的流体状态，可以得到确定流量下的节流孔直径。

表3 不同工况下的最优结构参数

当进口工况确定，满足上述表3中工况的节流孔直径分别为0.079mm、0.086mm、0.093mm、0.106mm、0.113mm、0.121mm。以表3中的翅片参数和小孔参数组合为新的制冷器，假定气库容积为300cm3，当气库初始压力为18MPa时，得到的流量变化与降温曲线如图3、图4所示，结构1～6分别对应表3中工况下得到的最优结构。

从图3中可以看出，在制冷器启动过程中，随着气库放气，制冷器的流量会出现短暂的上升趋势，随后很快转变为下降。节流孔直径逐渐增大，系统流量的上升幅度也较大。在制冷器运行一段时间后，不同结构对应的流量关系发生逆转，节流孔较大的结构，质量流量相对较小。这是由于初始阶段，节流前流体的压力还比较高，质量流量受小孔面积的影响比较大，等制冷器运行一段时间后，流量大的结构中的气库气体减少迅速，导致整个节流前流体的压力也相对较低，因此呈现出节流孔大的结构质量流量较小的结果。

如图4中降温曲线所示，节流孔较大的结构对应的冷端温度值较高、节流孔小的结构对应的冷端温度之较低，但不同结构的降温时间并没有确定的变化规律。节流孔最小的结构1进入恒定冷端温度区间时间最长，对应的冷端温度最低；结构3进入恒定冷端温度区间的时间最短，对应的冷端温度值比结构1和结构2略高。当冷端温度进入稳定阶段后，温度值基本保持稳定。随着制冷器工作时长增加，气库内体积变小、质量流量减少，节流孔最大的结构7冷端温度最先出现上升，脱离恒定温度区间的时间也最短。

图5为气库容积300cm3时，不同结构下对应的实时冷量变化。从冷端的冷量数值来看，冷端温度进入恒定后，冷量开始逐渐上升，在25s左右，所有结构对应的冷量值达到最大。此时，结构3的冷量值最大，结构2、4、5的冷量最大值比较接近，结构1和结构7的冷量最大值比较接近。随后，冷量进入迅速衰减期，在25～50s时间内，相同时刻的冷量大小分别对应的结构为结构3、2、1、4、5、6；在50s以后，相同时刻的冷量大小对应的结构分别为结构1、2、3、4、5、6。图5的冷量值呈现出这种结果，主要是受到系统流量和冷端温度的双重影响。

图3 流量变化曲线

图4 冷端温度变化曲线

图5 冷端冷量变化曲线

4 结论

本文中建立了J-T节流制冷器一维稳态数值模型，对制冷器中换热器的几何结构进行了单因素性能影响分析，结果表明换热器的翅片参数（肋高、肋厚和肋间距）和螺旋参数（螺旋直径、螺旋圈数）对换热器的性能具有明显的影响。论文还利用遗传算法主要对节流制冷器中的换热器翅片参数（肋高、肋厚和肋间距）进行了优化，结果表明：肋厚小、肋高大时，换热器能达到较大的冷端冷量和较小的熵产，且肋间距与肋厚之间存在2倍的最优结构。在气库容积为300cm3，初始压力为18MPa的工况下，肋厚0.1mm、肋节距0.222mm、肋高0.492mm、小孔直径0.093mm的结构组合，能够实现制冷器快速降温，能较长时间将冷端温度维持在90K以下，且冷端能提供的冷量较大。

[1] 陈晓屏. 微型低温制冷技术的现状和发展趋势[J]. 红外与激光工程, 2008, 37(1): 45-49.

CHEN Xiaoping. Status and trends of the cryocooler in IRFPA detector[J]., 2008, 37(1): 45-49.

[2] Maytal BZ. Performance of ideal flow regulated Joule-Thomson cryocooler[J]., 1994, 34(9): 723-726

[3] CHOU FC, PAI CF, CHIEN SB, et al. Preliminary experimental and numerical study of transient characteristics for a Joule-Thomson cryocooler[J]., 1995, 35(5): 311-316.

[4] XUE H, Ng KC, WANG JB. Performance evaluation of the recuperative heat exchanger in a miniature Joule=Thomson cooler[J]., 2001, 21(18): 1829-1844.

[5] NgKC, XUE H, WANG JB. Experimental and numerical study on a miniature Joule-Thomson cooler for steady-state characteristics[J]., 2002, 45(3): 609-618.

[6] CHUA H T, WANG X L, TEO H Y. A numerical study of the Hampson-type miniature Joule–Thomson cryocooler[J]., 2006, 49(3-4): 582-593.

[7] HONG Y J, Park S J, Choi Y D. A Numerical Study on Operating Characteristics of a Miniature Joule-Thomson Refrigerator[J]., 2010, 12(4): 41-45.

[8] Lerou PPPM, Veenstra T T, Burger J F, et al. Optimization of counterflow heat exchanger geometry through minimization of entropy generation[J]., 2005, 45: 659-669.

[9] Gupta P K, Kush P K, Tiwari A. Design and optimization of coil finned-tube heat exchangers for cryogenic applications[J]., 2007, 47(5-6): 322-332.

[10] CAO J, HOU Y, WANG W B, et al. Transient modeling and influence of operating parameters on thermodynamic performance of miniature Joule-Thomson cryocooler[J]., 2018(143): 1093-1100.

[11] Timmerhaus K D, Flynn T M.[M]. New York: Plenum Press, 1989.

Optimal Design of Miniature Joule-Thomson Cryocooler

CAO Jing1，HOU Yu1，LI Jiapeng2，CHEN Jun2，CHEN Shuangtao1，CHEN Liang1

(1.,,710049,;2.,650223,)

The Joule–Thomson (J–T) cryocooler is widely used in a variety of infrared devices. Maximizing the cooling capacity in finite structures is one of the foremost problems in J-T cryocooler miniaturization. In this study, a one-dimensional model based on the thermodynamic properties of real gas and heat leakage of components is established. The effects of three structural parameters (fin height, fin thickness, and fin pitch) used in a helical finned tube heat exchanger on the performance of a cryocooler are calculated and optimized using a genetic algorithm. The results show that the calculated data are in good agreement with the experimental data. In the specific working conditions and structural parameters employed, an increase in fin height and fin thickness would increase the entropy production and cooling capacity of the cold end of the heat exchanger, whereas an increase in fin pitch would have the opposite effect. Optimal parameters exist for maximizing the cooling capacity of the heat exchanger in this study. The analytical method established in this study could provide a simple and effective means of optimizing and designing a J–T in engineering applications.

Joule-Thomson cryocooler, finned tube heat exchanger, numerical simulation, optimized structure

TN215；TB65

A

1001-8891(2020)09-0893-06

2020-01-02；

2020-08-17.

曹菁（1989-），女，博士研究生，研究方向：制冷及低温工程。E-mail：caojing2011@stu.xjtu.edu.cn。

陈良（1984-），男，副教授，博导，研究方向：制冷及低温工程。E-mail：liangchen@mail.xjtu.edu.cn。

国家自然科学基金（51706169）；陕西高校青年创新团队。