沿程阻力实验误差原因分析及教学改进
2020-09-29张黎明许石青史文兵
张黎明,许石青,史文兵
(1. 贵州大学 矿业学院,贵州 贵阳 550025;2. 贵州大学 贵州省非金属矿产资源综合利用重点实验室,贵州 贵阳 550025;3. 贵州大学 资源与环境工程学院,贵州 贵阳 550025)
流体力学作为经典而又现代化的工程类专业基础学科,是许多工学专业的必修基础课[1-3],特别是在采矿工程、石油化工、土木工程、水电水利、机械工程等专业领域,流体力学更是构成整个专业知识结构的重要基础[4-5]。流体力学的教学主要包括基础理论教学和实验/实践教学两方面。实验/实践教学将内容抽象、涵盖面广的理论知识具体化、形象化,是理论知识与工程实际联系的纽带[3,6]。目前,各高校流体力学实验教学方法趋于多样化、个性化,例如,利用计算机模拟、3D 打印技术、虚拟仿真等先进教学方法、教学手段,实现流体力学实验的虚拟可视化[1,3,7-8]。然而,用传统实验方法进行流体力学实验仍是整个实验教学环节不可或缺的一部分,一般包括沿程阻力与局部阻力实验、雷诺实验等。
目前,我校矿业学院流体力学实验面向全院采矿工程、安全工程、矿物加工工程、矿物资源工程等专业的本科学生开设。其中,沿程阻力实验通过测定流体沿程阻力损失,使学生深入理解沿程损失产生的原因、规律,同时培养学生实践动手能力[8-9]和实验数据分析处理能力,实验仪器为传统有机玻璃材质实验仪器。
1 实验教学内容
通过测定沿程阻力损失、流体流量、平均流速等,加深对沿程阻力基本知识的理解。学生通过10 组实验,再通过数据分析和绘制流速与沿程阻力损失lgulghf曲线图,进一步分析沿程损失与平均流速的关系。
1.1 实验仪器
本实验所用的实验仪器如图1 所示。

图1 实验仪器简图
1.2 沿程水头损失测定
求截面1、2 之间的沿程阻力损失,列出两界面能量方程:
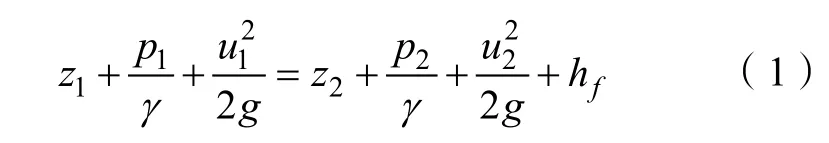
其中,z1、z2分别为1、2 截面的位置水头,P1、P2分别为1、2 截面的压力水头,γ 为水的重度(γ = ρg,ρ 为水密度),即为单位重量水的总势能;u1、u2分别为1、2 截面的流体平均流速,为相应截面的速度水头;为总水头。三者均为长度量纲。而流体由截面1 流到截面2,产生了能量损失,即沿程阻力损失。由式(1)计算出沿程阻力损失hf:
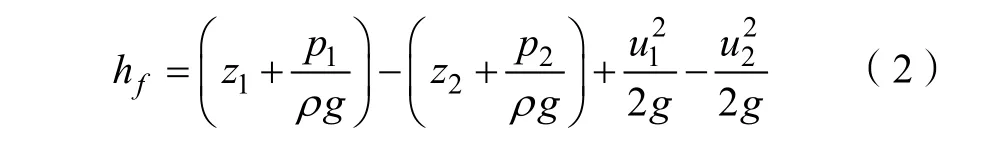
其中,由于1、2 截面管径相等,且流体流量相等,平均流速 u1= u2,则:

由此可得,实验条件下的沿程阻力损失可由静压水头高度读数直接测得,1、2 截面的水头之差即为沿程阻力损失。
1.3 流体平均流速测定
通过体积法测定两截面的平均流速。在一定时间t(单位s)内,流过截面的流体体积即为计量水箱中流体体积V,则流体单位时间平均流量为两个截面的平均流速为:

其中,A 为截面1、2 的面积,d 为截面1、2 的直径,此实验条件下 d1= d2, A1= A2。
1.4 实验结果示例
以某一组实验结果为例,实验测得沿程损失及流量、流速计算结果如表1 所示。

表1 沿程阻力测量及计算结果
根据实验结果作图lg u - lg hf,如图2 所示。将平均流速u 对数值lgu 作为横坐标,沿程损失hf的对数值lg hf作为纵坐标,描点后发现各点基本落于同一条直线上,通过作图软件Origin 作图并拟合后发现,该直线方程为 y = 1.975 3 x- 2.917 8,且相关性系数平方R2=0.992 8,接近1。
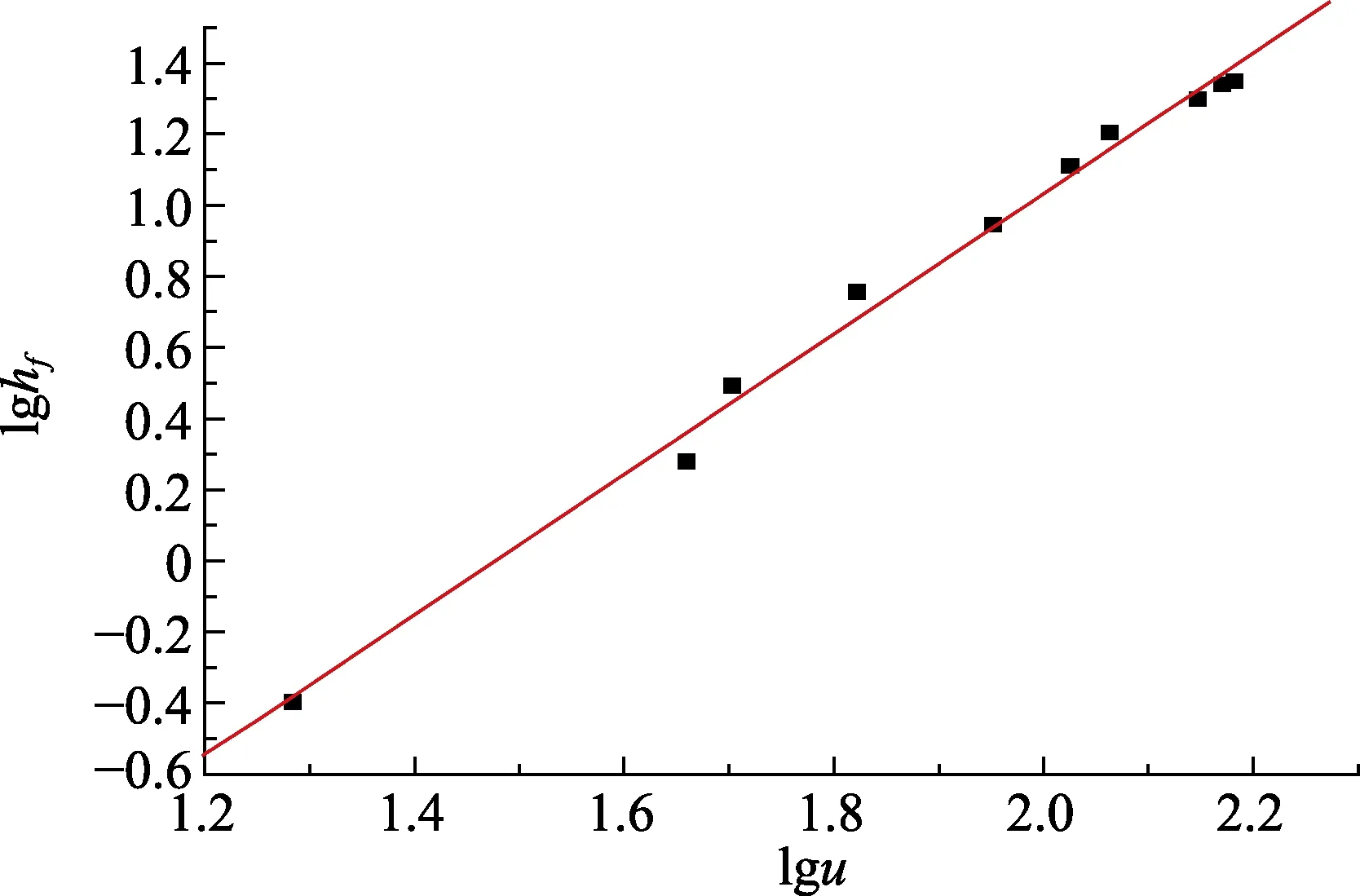
图2 lgu-lghf 描点拟合图
学生通过实验测量、数据记录、计算、作图,可以更深入理解沿程阻力损失与流体平均流速的关系,理想状态下,流体的沿程阻力为:
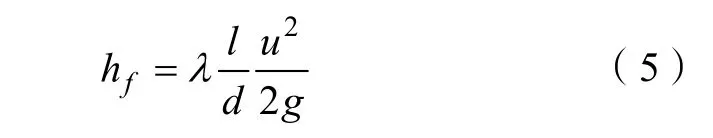
式(5)中,λ 为沿程阻力损失函数,l 为实验水管长度。式(5)等号两端同时取对数即为:

学生通过整个实验过程,既能学习沿程阻力的实验测量方法,又加深了对沿程阻力产生原因的理解,验证了沿程阻力与流速的关系,即沿程阻力损失与平均流速的平方成正比[9-10]。
2 实验误差原因
事故树分析法(fault tree analysis,FTA)是一种演绎推理法,由待研究的“事故”开始,通过层层分析最终找出导致特定“事故”发生的原因,以及各原因间的逻辑关系[11]。FTA 主要分析步骤为:(1)确定“特定事故”作为研究对象,即原因分析的源头,作为顶事件;(2)根据演绎分析的逻辑关系,编制事故树;(3)根据事故树进行布尔运算,计算得出其最小割集、最小径集以及结构重要度,对顶事件发生原因进行定性、定量分析;(4)根据分析结果提出减少顶事件发生概率的具体措施和方法。
随机抽取20 组学生实验结果,利用FTA 对实验失误原因进行分析。20 组实验结果的线性拟合方程相关系数平方,即决定系数R2如表2 所示,平均值=0.924 5,根据以往实验教学经验及整体实验结果,若R2<0.90 则认为该组实验出现较大失误,20 组中的第6、10、16 组为实验失误,失误组数共3 组。

表2 分析原因前的20 组实验拟合决定系数R2 统计
2.1 建立事故树
首先确定顶事件为实验失误。综合考虑实验整体效果,将相关系数平方R2≥0.90 作为实验基本成功的标准,以 R2<0.90 即“实验失误”作为事故树的顶事件,层层分析导致实验失误的原因。实验失误的原因可从实验仪器、操作过程、数据处理3 个方面进行分析。对每个方面进行详细分析,直到基本事件为止。
(1)实验仪器方面。实验仪器为有机玻璃材质,在长期使用过程中个别仪器出现管道老化、渗漏等状况。学生在实验操作过程中损坏仪器零部件的情况也时有发生,造成仪器连接处漏水或回水阀门损坏等。因此,实验仪器对实验失误的影响主要体现在计量水箱体积和实验水管两方面。水箱下部回水管可能有少量渗漏,采用秒表计时的体积法计算流量和流速,流体从实验水管流到水箱,可能发生水滴飞溅到箱壁的情况,造成计量体积的误差。
(2)实验操作过程。这方面的误差主要包括:水头读数误差、时间记录误差、水箱高度误差。两截面的水头高度以及计量水箱高度都应在水面平稳后、平视凹液面最低处的读数,否则会造成读数误差。应用秒表计时,应专注且计时精确,在实际教学中时常有学生未保留毫秒、微秒的现象,都可能造成计时误差。
(3)数据处理方面。这方面的误差主要包括:计算过程失误、作图失误、原始数据错误。计算过程保留有效数字较少将导致计算不精确,或由于粗心导致代入数据错误。用计算结果作图时,可能出现描点失误或线性拟合失误,导致无法表明沿程阻力与流速的关系,最终出现失误。如果未进行严格验算或出现验算错误等数据处理不当,会导致整个实验失误。
综上所述,实验失误事故树如图3 所示,各个事件如表3 所示。
2.2 事故树分析
根据上述事故树结构函数,对其作布尔代数运算:



图3 实验失误的事故树

表3 事故树事件

结果表明,导致实验失误的可能性有13 种,可见实验失误很容易发生。而事故树的最小径集只有一个,包含所有基本事件,表明避免失误发生的途径是唯一的,即尽量避免所有基本事件的发生。
3 事故树分析应用
尽管国内有的高校建立了较先进的流体力学实验教学平台,更新了实验仪器,采用了虚拟仿真技术、计算机模拟技术等,制定了个性化、启发式、创新性的实验教学内容[4,12-13],但有不少院校的流体力学实验仪器仍比较传统,更新缓慢[8]。未来的发展趋势将是实验手段的现代化,这将从根本上解决传统实验仪器、实验操作中难以避免的失误问题。
在目前实验条件下,即在不更换现有仪器的条件下,需要利用事故树分析结果,提高实验成功率,使学生能够通过沿程阻力实验加深对理论知识的理解。这就需要从各基本事件入手,减小基本事件同时发生的数量和概率。
(1)从仪器入手,提前检查仪器密封性,弥补可能渗漏的缺陷。对难以避免的误差,如水滴飞溅,尽量在流体平稳飞出水滴较少时测量流速。
(2)熟练和强化实验操作过程。实验前、实验中要强调水头读数、水箱读数的要点,避免产生较大误差,提醒学生注意秒表计时的准确性。
(3)数据处理方面,采用实验现场录入数据,并用计算机软件,如Excel、MATLAB、Origin 等计算、作图软件进行核算、验算,可以大大提高实验准确性。如发现个别测点与其他测点偏差较大,可以立即重新进行补测,及时避免失误发生,减少计算不精确、数据代入错误、人工作图失误等问题,培养学生自我检查误差来源、锻炼误差分析能力的习惯[14-15]。
综上,从实验仪器、操作过程、数据处理3 方面入手,将相关措施落实到后面的实验中,大大减小了实验误差,实验结果拟合直线相关系数平方(决定系数)R2均达到了0.90 以上,平均值为0.992 5,更接近1,比前次20 组的实验提高了7.36%,如表4 所示。
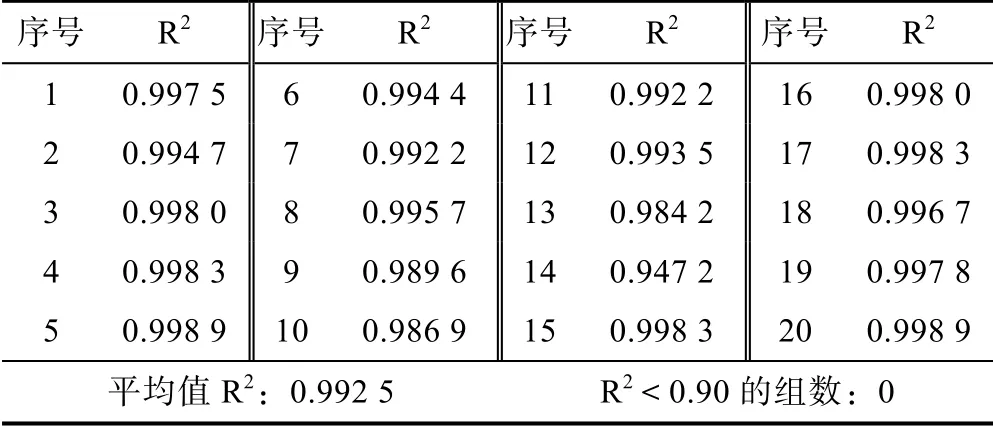
表4 分析原因后的20 组实验拟合决定系数R2 统计
4 结语
在实验教学中,导致学生实验出现失误、失败的原因众多且复杂,分析导致实验失误的因素至关重要。据此不仅可以防止误操作、降低实验失误概率,而且可以提高学生对实验研究过程的严谨专注。事故树分析法是可预先进行的、演绎的系统工程分析法,从待分析的顶事件出发,最终分析出导致实验失误的最基本因素,是一种行之有效的实验失误因素分析方法,适用于实验教学。
由于实验条件限制,在传统流体力学实验教学中,即在通过读数测定沿程阻力的实验条件下,应用事故树分析法,可逐步分析流体力学沿程阻力实验失误产生原因,找到导致失误发生的各个基本事件。分析发现,实验的成功需要操作者认真严谨,避开或减少一切导致失误的基本因素。从失误根本原因入手,指导教师应在实验前认真维护、检查实验仪器,对可能导致实验失误的重点部位进行详细排查,以保证仪器正常使用;在实验教学中,应指导学生在实验操作、数据处理过程中尽可能避免失误产生。
将事故树分析法作为实验误差分析方法引入实验教学,能够引导学生自主应用该系统分析方法分析实验失误产生的原因,从而提高实验成功率,并培养学生的综合分析能力。
