一个特殊的四维幂零左对称代数上的Rota-Baxter算子*

李黎明， 丁梦菲， 侯冬平

(云南师范大学 数学学院，云南 昆明 650500)

1 引 言

Rota-Baxter算子是由Baxter 在解决一个分析问题的过程中提出[1]，此后很快被应用到其他数学领域[2-4].最初，人们主要研究结合代数上的Rota-Baxter算子；随着研究的深入，Rota-Baxter算子很快被推广到其他代数体系上[5].

左对称代数(也称为预李代数)是一类非常重要的非结合代数，与很多数学学科和数学物理的许多领域都有密切的关系[6-11].文献[12]给出了所有2维复的左对称代数及大部分3维复数域上的左对称代数上权为0的Rota-Baxter算子;然而，对于更高维数的左对称代数上的Rota-Baxter算子，还知之甚少.

在文献[7]中，Kim利用左对称代数公式对所有4维幂零左对称代数进行了分类,给出了仅有的两个4维非对称无平移的幂零左对称代数结构

其中e1,e2,e3,e4为一组基，矩阵中的(i,j)元为ei与ej的乘积.

本文将给出四维复左对称代数A0上所有的权为零的Rota-Baxter算子，并以这些Rota-Baxter算子为基础，构造出一系列左对称代数结构.

2 基本概念

定义1设g是数域上的一个线性空间，在g中定义双线性乘法：(x,y)→[x,y]，满足等式

[x,y]=-[y,x]

(1)

[[x,y],z]+[[y,z],x]+[[z,x],y]=0

(2)

则称g是一个李代数,其中x,y,z∈g.

定义2设A是数域上的一个线性空间，在A中定义双线性乘法：(x,y)→x·y，满足等式

(x,y,z)=(y,x,z),∀x,y,z∈A

(3)

其中 (x,y,z)=(x·y)z-x·(y·z),则称A是一个左对称代数或预李代数.此时，定义李括号

[x,y]=xy-yx,∀x,y∈A

(4)

则(A，[,]) 是一个李代数，称为左对称代数A的邻接李代数，记为G(A).

定义3设A是复数域上的一个左对称代数,称线性变换R：A→A为A上的一个权为零的Rota-Baxter算子，如果R满足：

R(x)R(y)=R(R(x)y+xR(y)),x,y∈A

(5)

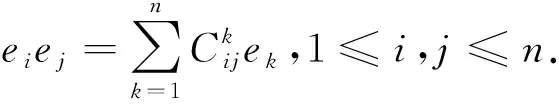
(6)

则R是A上的一个权为零的Rota-Baxter算子当且仅当{rij,1≤i,j≤n}满足以下方程：

(7)

证明：经过计算得到,对任意1≤i,j≤n,有

结合定义3，结论成立.

记

(8)

3 四维左对称代数 A0上的Rota-Baxter算子

命题1四维复左对称代数A0上的线性变换R，其中

(9)

则R是A0上的一个权为零的Rota-Baxter算子当且仅当{rij,1≤i,j≤n}满足以下方程

r13=r14=r34=r21=r23=r24=0

(10)

r12(r11-r33)=0

(11)

(12)

r12(r31+r43)=0

(13)

r11r44+r12r32-(r11+r44)r22=0

(14)

r12(r44-r33)=0

(15)

r11(r22+r33)-r22r33=0

(16)

r12(r22+r33)=0

(17)

r31(r22+r44)-r43(r11-r22)=0

(18)

r12r43-(r22+r44)r32=0

(19)

r22r44-(r22+r44)r33=0

(20)

r32(r11-r33)=0

(21)

(22)

r32(r43+r31)=0

(23)

(24)

r32(r33-r44)=0

(25)

r11r44-(r11+r44)r22=0

(26)

r42(r11-r33)=0

(27)

r42(r44-r33)=0

(28)

r43r33+r44r31-r42r12-r22(r31+r43)=0

(29)

(30)

(31)

证明:由性质1及

(1)由

可得

r14=0，r13r42-r21(r11+r44)=0，r11r44+r13r43-r22(r11+r44)=0

(2)由

联立r14=0，可得

r13=0

(3)由R(e2)R(e3)-R(R(e2)e3+e2R(e3))=0，结合r13=r14=0，可得

r23=r34=0，r11(r22+r33)-r22r33=0，r12(r22+r33)=0

(4)由R(e4)R(e2)-R(R(e4)e2+e4R(e2))=0，可得

r21=0

(5)由R(e1)R(e2)-R(R(e1)e2+e1R(e2))=0，可得

r24=0

如此，证明了方程(10)、(16)和(17)成立.同理也可以证明其余方程成立.

定理1四维复左对称代数A0上权为零的Rota-Baxter算子

记为R=(rij),有如下几类：

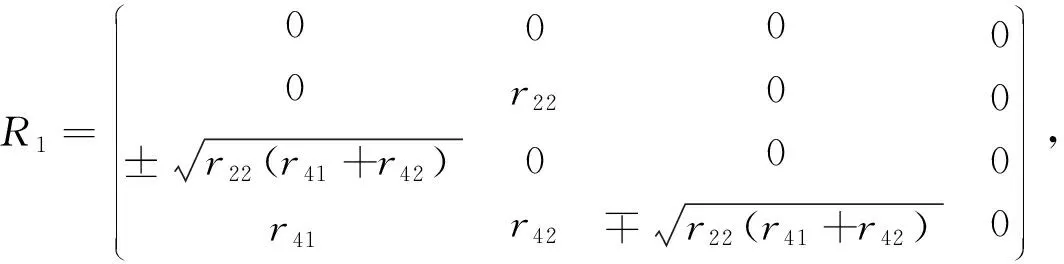
(32)

证明：(1)先证明r12=0.若r12≠0，则联立方程(11)、(15)和(17)可得

r11=r33=r44=-r22

联立方程(20)， 得r22=0,而由(12)有r22=-r12≠0,矛盾,所以r12=0. 同理可证r32=0.

(2)由r12=r32=0,方程 (10-31)化简为以下方程

r12=r13=r14=r21=r23=r24=r32=r34=0

(33)

r11r44-(r11+r44)r22=0

(34)

r11(r22+r33)-r22r33=0

(35)

r31(r22+r44)-r43(r11-r22)=0

(36)

r22r44-(r22+r44)r33=0

(37)

(38)

r31r44-r22(r31+r43)=0

(39)

r11r44-(r11+r44)r22=0

(40)

r42(r11-r33)=0

(41)

r42(r44-r33)=0

(42)

r43r33+r44r31-r22(r31+r43)=0

(43)

(44)

(45)

(3) 当r42≠0时,联立 (41-42)得r11=r33=r44,代入(37)得

r11=r33=r44=0

此时方程(33-45)同解于以下方程

故解得

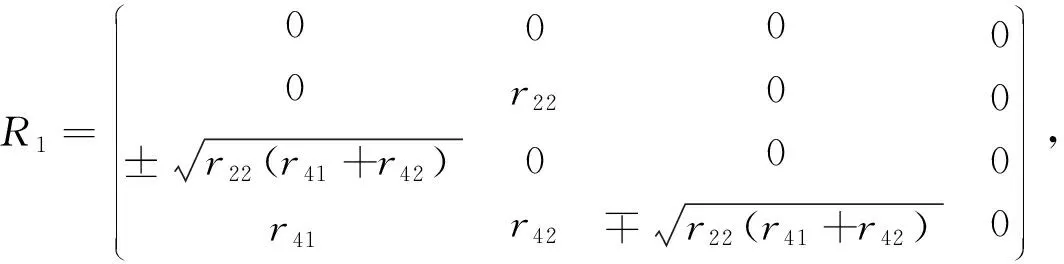
(4)当r22=r42=0时，由(38)得r33=0,由(34)得r11r44=0,代入(44)得r44=0， 代入(45)得到r43=0.此时，方程(33-45)都成立， 从而

(5)当r22≠0,r33=0,r42=0时,由(35)得r11r22=0，则r11=0，联立(44) 得r44=0, 此时方程 (33-45)同解于以下方程：

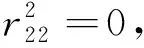
定理得证.

推论1：A0上不存在可逆的权为零的Rota-Baxter算子.

推论2：A0上不存在可逆的导子.

证明：由文献[12]知道，左对称代数上可逆的导子的逆映射是一个权为零的 Rota-Baxter算子,结合推论1知结论成立.

4 由四维左对称代数上的Rota-Baxter算子构造的左对称代数链

性质2[12]设(A，·)是一个左对称代数,R是(A，·) 上的一个Rota-Baxter算子,在线性空间A 上定义乘法

x*y=[R(x),y]=R(x)·y-y·R(y),∀x,y∈A

(46)

则(A,*) 也是一个左对称代数，且R也是(A,*) 上的一个Rota-Baxter算子.

称左对称代数(A,*) 为左对称代数(A,·) 与Rota-Baxter算子R相关的第一重代数.由性质2可知，从左对称代数(A，·) 和(A，·) 的一个Rota-Baxter算子R出发，可以在线性空间A上定义一个左对称代数的系列 (A，R,*k)(k≥1),其中

x*1y=x*y=[R(x),y]=R(x)·y-y·R(y),∀x,y∈A

(47)

x*k+1y=[R(x),y]k=R(x)*ky-y*kR(y),∀x,y∈A

(48)

称(A，R,*k) 为 (A，·) 的第k重代数.

性质3[12]设(A，·)是一个左对称代数,R是(A，·) 上的一个Rota-Baxter算子,(A，R,*k) 为 (A,·) 的第k重代数，则

(49)

(50)

定理2由四维复左对称代数A0和它上面的 Rota-Baxter算子出发，得到的左对称代数系列有

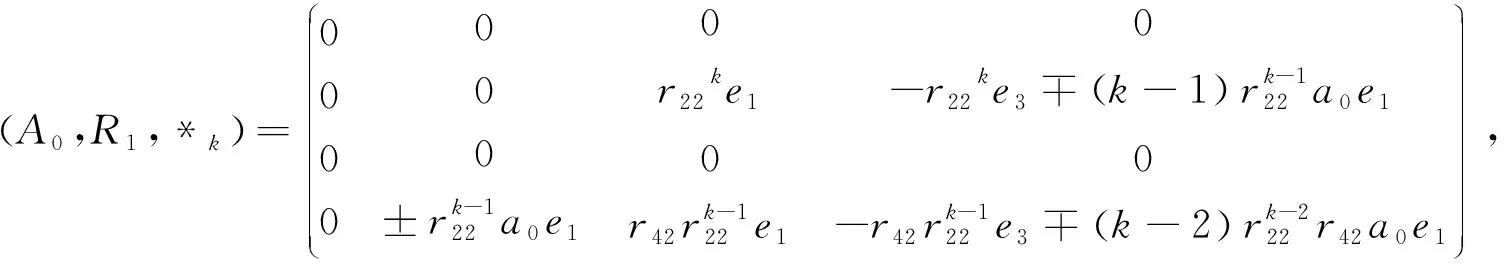
(2) (A0，R2，*k)k≥1为零代数(任意两元素的乘积为零).

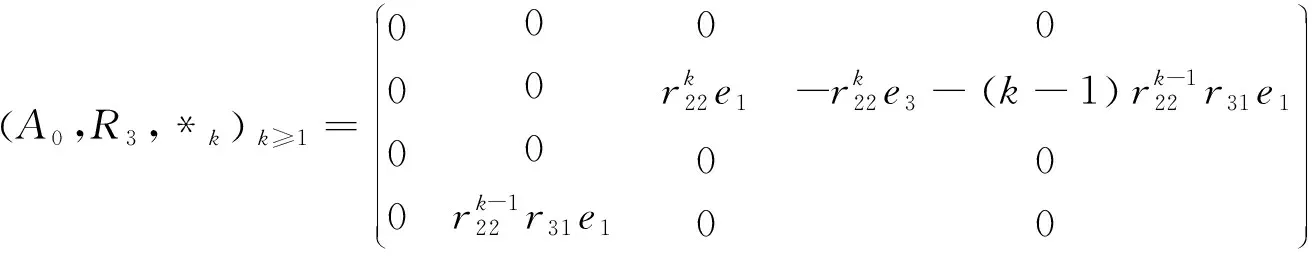
证明：以第(1)种情形为例证明.

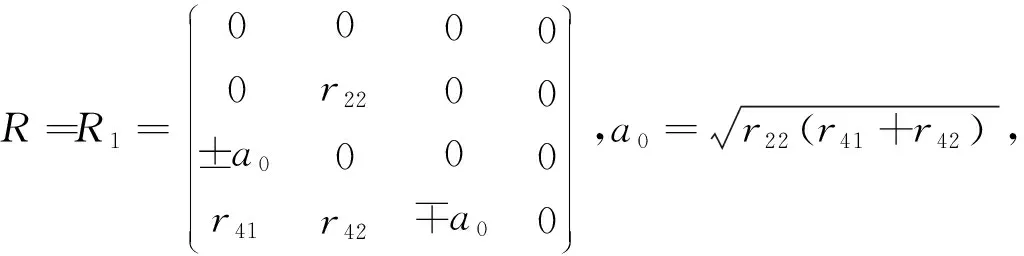
R(e2)=r22e2;R(e3)=±a0e1;R(e4)=r41e1+r42e2∓a0e3;R(e1)=0

由性质3可以得到

e2*1e3=R(e2)e3-e3R(e2)=r22e1;e2*1e4=R(e2)e4-e4R(e2)=-r22e3

e4*1e2=R(e4)e2-e2R(e4)=±a0e1；e4*1e3=R(e4)e3-e3R(e4)=r42e1

e4*1e4=R(e4)e4-e4R(e4) =-r42e3

其余，ei*1ej=0，从而可得

假设

结合性质3可得

e2*k+1e3=R(e2)*ke3-e3*kR(e2)==r22k+1e1

e4*k+1e3=R(e4)*ke3-e3*kR(e4)=r42r22ke1

其余，ei*k+1ej=0，从而得到

由数学归纳法可得

特别，r41+r42=0，r42≠0时,a0=0,此时

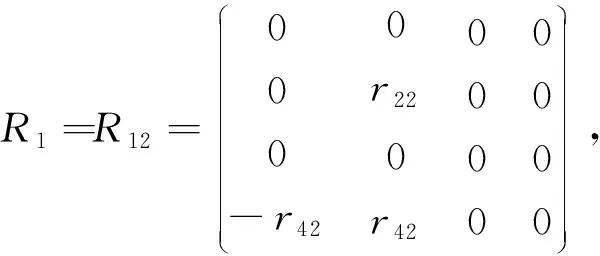
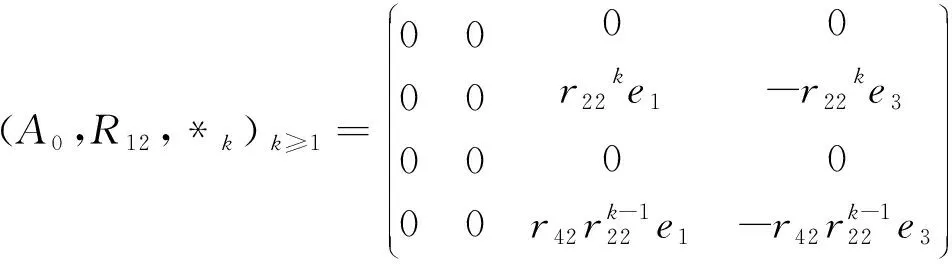
建立A0上的可逆线性变换

易知

同理，可以证明其他情形的结论.

5 结 语

给出了一个特殊的四维左对称代数上所有的权为0的Rota-Baxter算子，并且以此为基础进一步构造出一系列左对称代数.这对于非结合代数上的Rota-Baxter算子的研究有一定的意义.