融合Kinect与γ相机图像的放射性区域重建与定位

王 刚，肖宇峰，郑又能，田星皓

（1.西南科技大学 信息工程学院，四川 绵阳 621010；2.中国原子能科学研究院核技术应用研究所，北京 102413）

引言

随着我国核工业的快速发展，核设施和放射源在能源、军事、医疗、工业等领域的应用日益广泛。在核设施退役、核事故应急处置中，放射性区域的重建与定位能帮助作业人员直观、准确地分析核辐射环境，提高退役去污、应急处置作业的效率。

目前对放射性区域重建主要有康普顿相机成像和γ相机成像两种方式[1]。国外研究中，普遍采用康普顿成像仪结合深度相机或者激光雷达实现辐射场的三维重建[2-3]。文献[4]提出的SDF（scene data fusion）方法使用两个3D位置敏感高纯度锗探测器组成移动康普顿成像仪，结合同时定位与地图创建（simultaneous localization and mapping，SLAM）算法能够近乎实时重建未知辐射环境的三维场景图，其中SLAM算法可以实时提供辐射场景的三维模型，迭代算法用于重建放射源的三维分布模型。SDF 方法实时提供了放射源的剂量分布和位置信息，极大地增强了辐射场景建图的适用性，但是其结果未对成像效率和精度进行优化。在此思想上，Haefner 等人使用高效多模成像仪（highefficiency multimode imager，HEMI）与Kinect相机构成手持式移动平台，融合γ 射线数据和视觉数据，可以实时生成精确的放射源三维分布模型，但未对放射源位置信息进行量化[5]；Lee 等人使用康普顿相机和激光雷达搭载在移动机器人上，构建了基于体素网格的辐射图，多源定位的平均误差在0.2 m以内[6]。

相比之下，基于γ相机三维重建技术的报道和研究不多。在国内，中国工程物理研究院材料研究所发展了针对点源的γ相机重建技术[7-8]。γ相机是一种高效准确的在线测量仪器，利用光学成像和射线探测机理合成放射源剂量分布图像[9]，为放射性物质的定位、搜寻及后续处置提供依据。然而γ相机只能得到放射源的二维图像[10]，用二维图像重构核污染位置三维分布，是实现快速测定放射性区域污染位置与分布的重要技术。对此朱宁等人采用最大似然期望最大化（maximum likelihood expectation maximization，MLEM）算法，通过模拟实验重建出了放射性体源的三维位置和形状分布[11]。但这一结果没有与周围环境信息融合，对放射性分布的描绘尚不充分。

根据上述情况，本文提出了基于Kinect与γ相机图像信息融合的放射性区域重建与定位方法。首先，构建Kinect与γ相机组合成像模型并完成其联合标定；接着构建辐射场景稠密点云地图并得到Kinect位姿数据；然后提取γ相机图像中放射性分布信息，根据联合标定参数生成放射性区域的点云，并依据Kinect位姿与辐射场景点云地图融合；最后，用最小包围盒确定放射性区域，对中心位置进行计算。本文在真实放射性环境中开展实验，重构了包含放射源三维分布模型的辐射场景点云地图，最终实现了放射性区域的三维可视化。测试结果证明本文方法可行，具有一定的准确度。

1 方法

1.1 放射性区域重建与定位方案

本文采用的Kinect版本是Microsoft 研发的Kinect V2[12]；γ相机是中国原子能研究院研制的全自动γ 射线扫描成像系统，型号为CIAE-ASC。该γ相机以等角度扫描的方式探测区域内各个点的γ 射线强度，形成二维强度分布图，并将放射源位置与实际环境图像集成显示[13]。

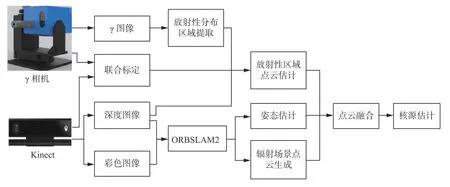
图1 放射性区域重建与定位方案Fig.1 Scheme of reconstruction and localization for radioactive area

基于上述平台，本文设计了如图1所示的放射性区域重建与定位方案。Kinect 能以30帧/s的速率同时采集分辨率为1 920×1 080像素的彩色图像和512×424像素的深度图像，利用同一时间戳的彩色图和深度图构建辐射环境地图、估计Kinect位姿。γ相机能采集分辨率为1 920×1 080像素的γ图像，提取γ图像放射性分布区域，再将其根据联合标定结果映射到与γ图像对应时间戳的深度图中得到其点云，并依据Kinect位姿信息与辐射场景点云融合。基于最小包围盒估计放射性区域点云中心位置，对放射源进行三维定位。

1.2 Kinect与γ相机协作基本原理

作为一类专用于核辐射环境成像的特殊设备，γ相机与常规成像设备组合工作的情形很少见。为更好解释两台相机协作工作原理，基于图2的安装结构，下文对相机组合成像模型、联合标定方法进行描述。

图2 两台相机的安装结构Fig.2 Installation structure of two cameras

1.2.1 Kinect与γ相机组合成像模型

图3 相机组合成像模型Fig.3 Camera combined imaging model

实际工作中，Kinect 安装在γ相机顶部，并保持两个相机有尽可能多的共视区域。基于图2的安装结构和相机针孔模型，构建了如图3所示的相机组合成像模型。Kinect 坐标系{D}为OdXdYdZd，世界坐标系{W}（惯性坐标系）为OwXwYwZw，γ相机坐标系{γ}为OγXγYγZγ，图像坐标系为OXY，像素坐标系为ouv。{W}里一点Pw像素点为m，{D}下的点可通过Kinect位姿Tw，ci转换到{W}。{γ}与{D}存在一个欧式变换关系，本文用Rγd、tγd描述γ相机相对于Kinect的旋转和平移矩阵，可通过联合标定获得。

1.2.2 Kinect与γ相机联合标定

对Kinect和γ相机联合标定，获取两相机的内参及其相对位置关系Rγd、tγd，才能实现γ相机图像中放射性区域到Kinect 深度图像的精准对齐。本文采用基于平面棋盘图像的标定方法，实现了Kinect和γ相机的联合标定。

联合标定主要步骤如下：

1） 图片获取：选取内角点为11×8的棋盘格作为靶标，如图4所示。移动靶标，用固定好位置的Kinect和γ相机，拍摄20幅不同位置不同角度的棋盘格图片。

图4 棋盘格标定板Fig.4 Chessboard calibration plate

2） Kinect和γ相机的内参获取：分别使用γ相机图像和Kinect 强度图检测内角点，将角点像素坐标与其三维坐标相对应。角点的像素坐标作为实际值，三维坐标经相机内外参投影得到的像素值作为观测值，通过最小化实际值和观测值的位置求解最大似然估计问题得到最优参数：相机内参K和外参Ri、ti。最大似然估计的评价函数定义为

式中：n为棋盘格图像张数；m为棋盘格角点数；xij为第i张棋盘格图像第j个角点的像素坐标；Xj为第j个角点的三维坐标；πs（·）为从 ℜ3→ℜ2的投影函数，计算公式如（2）式：

3） 相机间相对位置估计：运用最小二乘法求解γ相机棋盘格角点在Kinect 视图上的最小重投影误差，得到联合标定的最优解，计算公式如（3）式：

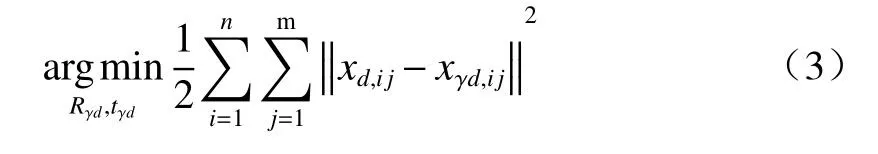
式中：xd，ij为Kinect 第i张强度图像的第j个角点坐标；xγd，ij为第i张γ相机图像的第j个角点坐标xγ，ij在对应Kinect 强度图上的投影坐标，计算公式如（4）式：

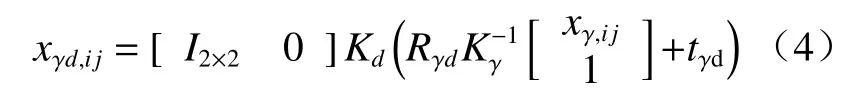
式中：Kγ、Kd分别是γ相机和Kinect的内参矩阵；I为单位矩阵。

按照上述联合标定步骤，得到Kinect和γ相机的内参结果如表1所示，联合标定的结果如表2所示，单张图像的重投影误差结果如图5所示，平均误差为0.154 63个像素，满足后续图像融合要求。

表1 单个相机标定相机内参及重投影误差Table1 Intrinsic parameter and re-projection error in single camera calibration

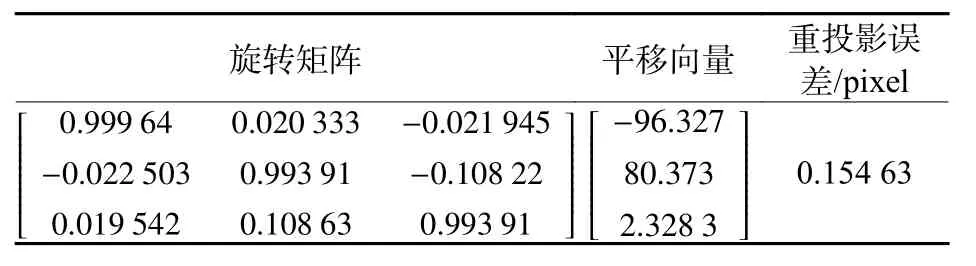
表2 联合标定的两个相机位置关系及重投影误差Table2 Position relation and re-projection error in joint calibration between two cameras

1.3 基于Kinect 的放射性环境点云地图构建

现有的ORB-SLAM2[14]方法可用于构建环境的三维稀疏特征地图，其关键帧保存了对应的彩色图像、深度图像和相机位姿，但因为特征稀疏不利于放射性区域的完整重建。在该方法的基础上，本文对关键帧的所有像素进行点云重建，构建放射性场景的稠密点云地图。

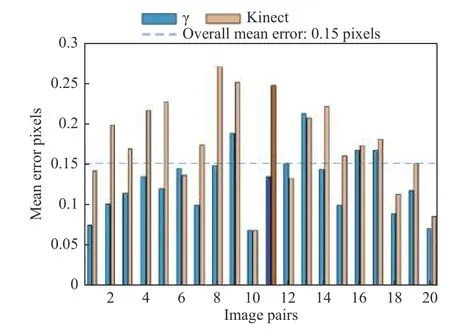
图5 联合标定重投影误差Fig.5 Re-projection error of joint calibration

在图3相机组合成像模型中，设{W}空间一点Pw（x，y，z）的二维像素坐标为m（u，v）。根据二维彩色图像和深度图像计算三维点云的公式如（5）式：

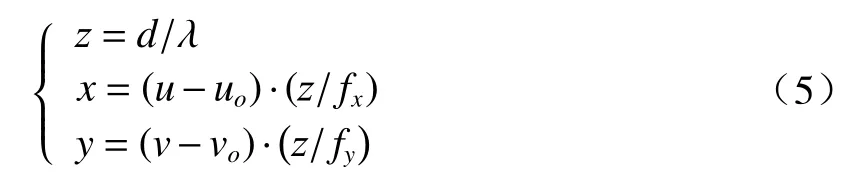
式中：fx、fy分别为u轴和v轴上的归一化焦距；（uo，vo）为图像主点坐标；d为Kinect 测得目标点的距离（单位为mm）；λ为实际距离与测得距离的比例系数，取值为1000。

从{D}到{W}的点云变换公式为

式中：Xci，j为第i个关键帧坐标系上的点云，Tw，ci为第i个关键帧的位姿，Xw，j是Xci，j变换后在{W}上的点云。

当Kinect 运动产生新的关键帧时，构建新的局部地图。待系统运行结束，将所有的局部地图整合为完整的地图。至此可以得到全局一致性的放射性环境稠密点云地图和精确Kinect 相机位姿。

1.4 多相机图像信息融合的放射性区域点云生成

由γ相机成像原理可知，放射源图像是叠加在其光学图像上的，所以可将γ图像中的放射性区域根据联合标定参数投影到对应Kinect 深度图中得到其点云，最后依据对应的关键帧位姿将其融合到辐射场景点云地图中。

1.4.1 γ图像中放射性分布信息提取

γ相机提供包含放射源的图像和背景图像，如图6（a）、6（b）所示。于是采用背景减除法用包含放射源信息的图像减去背景图像，得到放射性区域，即：

式中：Iγ表示包含放射源信息的伽玛图像；Ib表示背景图像；I表示放射性区域。

图6 放射性区域轮廓提取Fig.6 Contour extraction of radioactive area

对放射性区域进行灰度化，然后进行阈值处理，得到放射性区域的二值图像，如图6（c）所示。

其中：I（x，y）表示像素点（x，y）的灰度值，T为自适应灰度阈值。得到放射性区域的二值图像后，对其进行轮廓提取，结果如图6（d）所示。

1.4.2 融合放射性分布信息的点云生成方法

设放射性分布区域轮廓内一点像素坐标为Pγ=（uγ，vγ，1）T，对应深度图中的坐标为Pd=（ud，vd，1）T，对应三维空间点坐标为Pw=（Xw，Yw，Zw）T，由相机针孔模型得：

其中外参Rγ和tγ是{γ}相对于{W}的旋转和平移矩阵，同理对于Kinect的对应点有：

其中外参Rd和td是{D}相对于{W}的旋转和平移矩阵，联立式子（9）和（10）得：

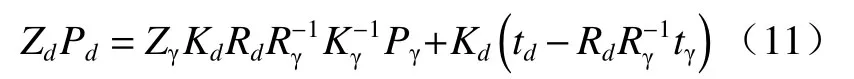
记

则（11）式可以简化为

将联合标定结果Rγd、tγd代入（13）式可以计算出γ相机视野下的深度值Zγ，进而得到该点点云。

设第i张γ图像放射性分布区域轮廓内第j个像素点的点云为Xγ，ij，在{W}下坐标是Xwγ，j，则有如下计算公式：

其中Tw，ci表示第i张γ图像对应的关键帧位姿，可由1.3节得到。遍历γ图像中放射性分布区域内所有像素点，得到该张γ图像在世界坐标系下的点云。

由于有测量误差以及深度配准误差，需对点云进行滤波处理：以点云质心为中心点，选取放射性分布区域的质心和轮廓点集中距离质心最远的点，以该两点距离为半径r，剔除大于r的点云。

对每张γ图像采取上述操作，至此可以建立包含放射源三维分布重建模型的辐射场景点云地图。

1.5 基于最小包围盒的放射性区域中心位置估计

主元分析法（principal component analysis，PCA）是求点集最小包围盒的常用方法，由于包围球的紧密性不够好，因此本文采用长方体包围盒确定放射性区域点云的最小区域。

设世界坐标下放射性区域的点云由Xwγ={Xwγ，1，Xwγ，2，…，Xwγ，j，…，Xwγ，J}组成，令放射性区域的中心点为

其中J表示放射性区域点云数目。放射性区域的协方差矩阵可以表示为

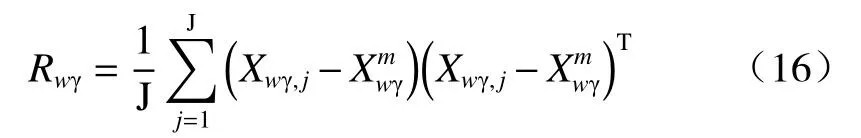
由于协方差矩阵是实对称矩阵，故其有3个非负特征值λ1、λ2、λ3，对应特征向量为u、v、w。将每个特征向量进行正交标准化结合质心坐标组成坐标变换矩阵C。设Xwγ经过坐标变换矩阵转化到主方向坐标系下的点云为Xcγ，其计算公式如（17）式：

为计算Xwγ的最小包围盒顶点坐标，需先计算主方向坐标系下Xcγ的轴向包围盒。取Xcγ中各坐标分量的最小值和最大值，构造点和以Pcγmin和Pcγmax为对角顶点建立轴向包围盒。根据轴向包围盒的各个顶点信息，利用（18）式将各个顶点转化为{W}下的点，最终获得点云Xwγ的最小包围盒。

其中Pw，k，Pc，k分别表示{W}下和主方向坐标系下的包围盒顶点，k=1，2，…，8。

2 实验

利用C++语言、OpenCV3.4.0函数库和PCL点云函数库实现了上述算法，并开展了实验测试。计算机采用Intel的3.20 GHz（4核）处理器，内存容量为4 GB，操作系统为Ubuntu 16.04。

由于γ相机是基于实时扫描的系统，在采集γ相机图像期间暂停点云地图构建，等γ相机采集完该位置之后就复位到暂停前的位置。这样的实验策略可确保同一时间戳的γ相机和Kinect 实现数据同步，确保生成的放射性区域的点云与环境地图能够实现空间对齐。

2.1 完整的辐射场景点云效果

在8×12 m2大小的实验室环境中，基于Kinect构建的完整辐射场景稠密点云地图如图7所示。从图7可以看出，点云地图和实际三维环境相符，没有出现地图重叠和变形等情况，并且地图中的暖气管、椅子、纸箱等杂物清晰可见。其中红色点云代表Kinect 运动期间光心坐标在全局地图中的位置，即运动轨迹。在整个实验中，系统共处理了2 510张视频帧，关键帧数目为164帧，FPS（frames per second）为19帧/s。

图7 辐射场景重建效果Fig.7 Radioactive scene reconstruction effect

目前，针对重建点云地图的精度评定方式没有固定原则。本文以中误差作为评价点云地图精度的标准[15]。选取门、显示屏、纸箱3个规则形状特征物，利用钢尺测量所选特征物的实际尺寸，用Cloud Compare 软件在点云中量取相应特征物的尺寸，以两者差值作为Δ 计算标准。从表3可以看出特征物的差值都在厘米级，经过实验对比，最终得到的特征物尺寸中误差为0.016 m。由此可见，重建的辐射场景点云地图精度较高。

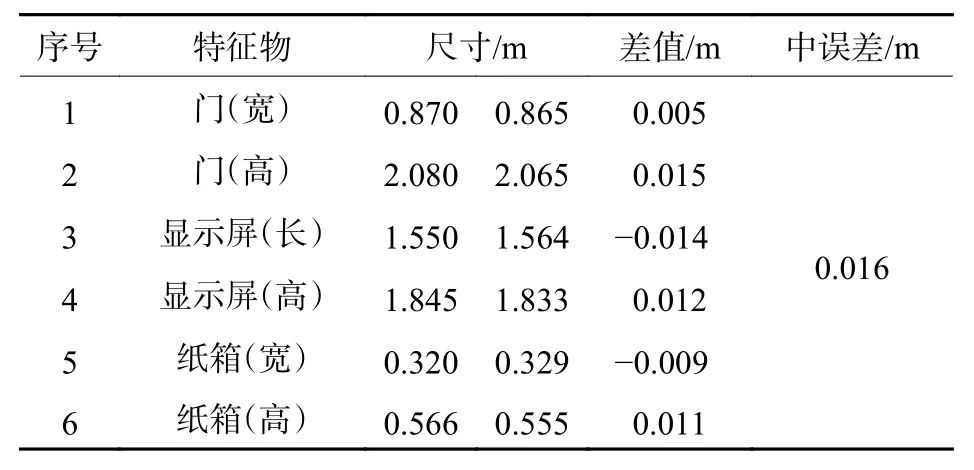
表3 特征物体尺寸对比Table3 Size comparison of feature objects

2.2 测试放射性区域点云生成效果

为了生成放射性区域点云，实验中，对活度为3 mCi的137Cs 放射源，γ相机在不同位置以不同角度采集了8 张γ图像，如图8所示。

图8 γ图像数据Fig.8 Data of γ images

本节选取如图9（a）所示的一张γ图像，分析其点云生成过程。图9（b）为图9（a）中的放射性区域所对应的二值图，其中白色区域是放射性区域；图9（c）为将γ图像中的放射性区域投影到已融合深度信息的彩色图像，并用线条描绘出了放射性区域轮廓。对轮廓里的点根据（13）和（14）式生成放射性区域的点云，图9（d）是图9（a）中的放射性区域所对应的点云。

图9 放射性区域点云生成过程Fig.9 Point cloud generation process of radioactive area

将8 张γ相机图像对应的放射性区域点云根据各自关键帧位姿信息融合到环境地图中，得到如图10所示的融合放射性区域点云的场景图，其中黄色区域代表放射性区域的点云模型，8个绿色的点代表γ相机采集γ图像时在辐射场景点云模型中的位置。

图10 融和放射性区域点云的场景图Fig.10 Scene diagram of point cloud in fusion radioactive area

2.3 测试放射性区域定位准确性和稳定性

为确定放射性区域点云的三维空间分布区域，采用基于主元分析法的最小包围盒算法测试放射性区域。如图10所示，箭头表示放射源的位置，右上角矩形区域表示放大的包围盒。从实验效果图可以看出，放射性区域点云分布在放射源周围，最小包围盒可以包围所有的放射性区域的点云，没有漏掉，证明了最小包围盒算法的可行性。

在同一室内环境中，采取相同的实验策略进行3组测试，采用实际值和估计值的距离作为误差度量最小包围盒的定位精度。3次实验的真实位置、估计位置以及误差见表4，误差控制在0.15 m以内。采用真实位置和估计位置的RMSE（root mean squared error）度量放射源的定位精度，均方根误差计算公式为

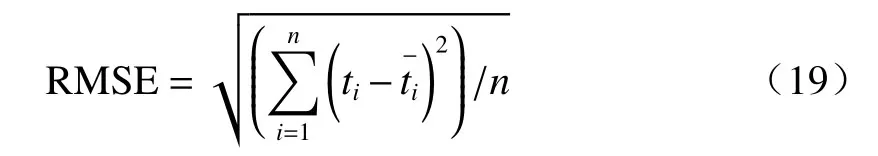
式中：ti、分别为估计位置和真实位置；n=3；均方根误差为0.11 m。由此得出，最小包围盒的中心坐标可以准确估计放射源的位置，证明了最小包围盒算法对于放射性区域定位的准确性和稳定性。

传统基于最小二乘法[16]、最大似然估计法[17]、融合-迭代[18]的辐射源定位算法已取得较好的二维定位效果，本文提出的方法可对放射源三维定位。相比文献[6]采用康普顿相机结合激光雷达实现的放射源三维定位方法，本文方法更加经济实惠。取文献[6]中137Cs 相关实验数据，误差对比如表5所示。从表5得出，文献[6]在小场景中取得较好定位效果，在相对更大场景中却不适用；而本文方法在较大场景中定位精度较高。

表5 两种不同方法定位误差对比Table5 Comparison of error by 2 different methods

3 结论

本文应用Kinect 创建室内环境地图并获取位姿信息，同时通过γ相机采集放射源的二维分布图像，将这两种视觉传感器集成到数据采集和算法处理框架中，完成对放射性区域的重建与定位。从实验数据的重建结果来看，可以在少量γ相机图像的情况下重构放射源三维分布模型，并且能与辐射场景地图融合，利用最小包围盒算法确定放射源分布区域。在获取放射性区域重建模型后，融合放射源强度信息将会是今后研究的重点。