朗伯双球的激光后向二维散射成像仿真

宫彦军 陈意强 史小飞

（1.湖南科技学院 电子与信息工程学院，湖南 永州 425199；2.湖南科技学院 图书馆，湖南 永州 425199）

蔡能斌等利用紫外激光成像技术，设计提取现场可能存在指纹的方案，并对方案并进行验证[1]。通过激光成像雷达的距离像可以实现目标的识别[2]。本文研究的是目标激光后向二维散射成像仿真，闫小伟等研究三维激光成像技术[3]。激光可用于空间碎片的高分辨二维成像，用于观测空间碎片[4]。激光成像制导是一种精确的制导方式[5]。宫彦军等研究朗伯圆锥和朗伯锥柱的激光后向二维散射成像仿真，计算的目标都是凸体[6-7]。本文研究朗伯双球激光后向二维散射成像仿真，双球作为一个整体目标，不是凸体，激光从有的方向入射时，2 个球之间存在遮挡。本文在笛卡儿直角坐标系下进行激光后向二维散射成像仿真的计算，利用射线跟踪判断2 个球之间是否存在遮挡，判断一个球上的面元是否被另外一个球遮挡。

1 双球激光后向二维散射强度像的计算公式

1.1 坐标系

1.1.1 本地坐标系

本文研究朗伯双球的激光后向二维散射成像的仿真，这里的激光后向方向就是激光入射方向的反方向。设球1 的半径为R1，球2 的半径为R2。设球之间的距离为S，是2 个球上最近的2 个点之间的距离。选2 个球上最近的2 个点的中点为坐标原点，用O 表示，2 个球的球心连线为X 轴，球1 的球心指向球2的球心的方向为X 轴正向，即球1 在X 轴的负半轴。选一个与X 轴垂直的方向为Y 轴正向，X 轴和Y 轴确定后，Z 轴也就确定了，这个笛卡儿直角坐标系为本地坐标系，是右手坐标系。本地坐标系的坐标用x，y，z 表示。Oxyz 为本地坐标系。球1 在本地坐标系的位置矢量为(－R1－S/2, 0, 0)，球2 在本地坐标系的位置矢量为(R2+S/2, 0, 0)。2 个球的球心距离为|R1+R2+S|。

1.1.2 成像坐标系

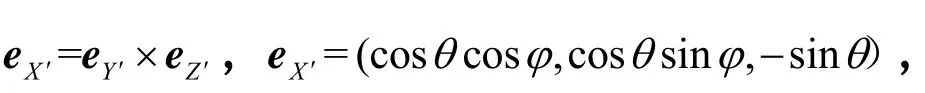
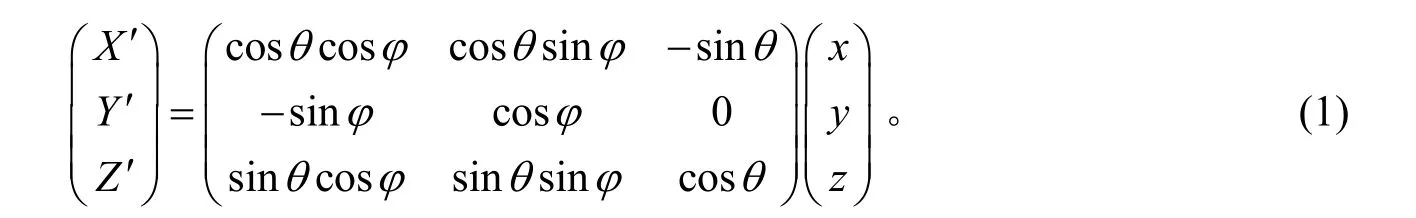
1.1.3 目标坐标系

分别以2 个球的球心为坐标系的原点，坐标轴与成像坐标系的坐标轴一致，建立2 个球的目标坐标系。

1.2 光强公式

1.2.1 激光雷达方程

一个激光雷达接收系统，接收器接收到目标激光散射的强度表达式为

式(2)中的Pt为发射机的发射功率，K0是一个常数，σ 为目标激光雷达横截面。

1.2.2 双球表面面元的激光后向散射强度

为了计算双球的激光后向散射强度，需要计算双球表面上的所有可照射面元的后向散射强度之和，目标表面面元在激光入射方向的反方向上的激光雷达横截面，即后向激光雷达横截面为

式(3)中 fr(β )为目标表面材料在激光入射方向反方向的双向反射分布函数，即激光后向双向反射分布函数，依赖于双球表面的材料，是双球表面面元的本地入射角β 的函数，β 是激光入射方向的反方向与双球表面的面元法线的夹角，双球表面的面元法线有2 个方向，一个指向球的里面，一个指向球的外面，这里的法线是指向外面的， AΔ 为面元的面积。

本文计算的激光后向二维散射强度像是平面波激光照射，发射的激光功率tP 为常数，用iI 表示。把iI和式(3)代入式(2)得双球的可照射表面面元的激光后向散射强度公式为

式(4)中 K =K0Ii，K 为常数。本文研究的是朗伯双球的激光后向二维散射强度像，双球表面材料为朗伯表面， fr(β )是一个常数， fr(β )= kL。对于凸目标，满足cos β ＞ 0的面元就可以被照射到，否则没有被照射到。

1.2.3 双球的激光后向散射强度

本文在每个球的目标坐标系下计算，球的目标坐标系的原点为每个球各自的球心，坐标轴与成像坐标系的坐标轴一致，双球表面面元的激光后向散射强度为

式(5)中nz为面元法线n 的笛卡儿坐标系Z 轴的分量。dX，dY 分别为面元在球的目标坐标系的XOY平面投影的X 轴、Y 轴投影长度。球在自己的目标坐标系的方程为

式(6)中的R 为球的半径。在目标坐标系下球的法线n 为

激光的入射方向为目标坐标系的Z 轴正向，其单位方向矢量g，在目标坐标系下计算，则 g =（0 ,0,1），cos β =( - g ).n= -Z /R 。 nz=Z/R，代入式(5)，双球表面面元的激光后向散射强度的计算公式为

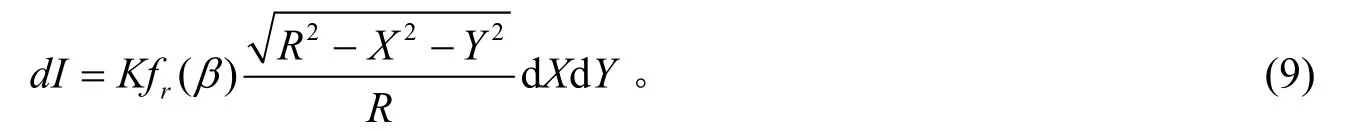
对式(9)在球的表面进行积分，球的激光后向散射强度为

1.3 不考虑遮挡的双球激光后向二维散射强度像的计算公式

根据式(10)，球1 的激光后向二维散射强度像的计算公式为

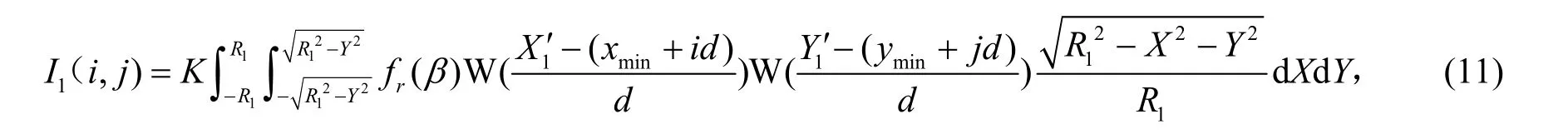
式(11)中 1X′，1Y′分别为球1 的表面面元位置矢量在成像坐标系的X 轴、Y 轴分量。式(11)中d 为成像分辨率。式(11)中i，j 分别为强度所在行、列位置，i=1，2，…，m；j=1，2，…，n。其中，m 为图像的像素点行数，n 为图像的像素点列数。窗函数W(x）为

球1 的球心在本地坐标系的位置矢量为 (- R1- S/2,0,0)，由式(1)，球1 的球心在成像坐标系的位置矢量为

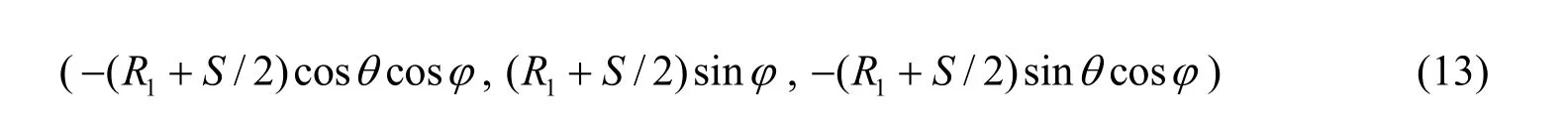
根据式(13)得式(11)中 1X′，1Y′为

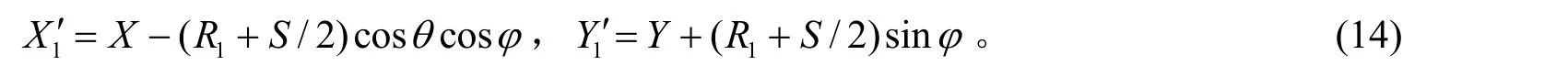
根据式(10)，球2 的激光后向二维散射强度像的计算公式为

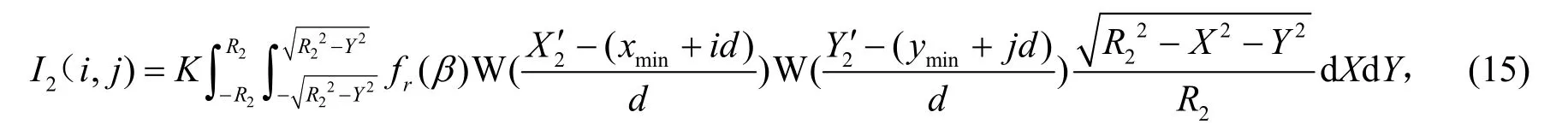
式(15)中2X′，2Y′为球2 的表面面元位置矢量在成像坐标系的X 轴、Y 轴分量。式(15)中d 为成像分辨率。球2 的球心在本地坐标系的位置矢量为 ( R2+ S /2,0,0)，由式(1)，球2 的球心在成像坐标系的位置矢量为

根据式(16)得式(15)中 2X′，2Y′为

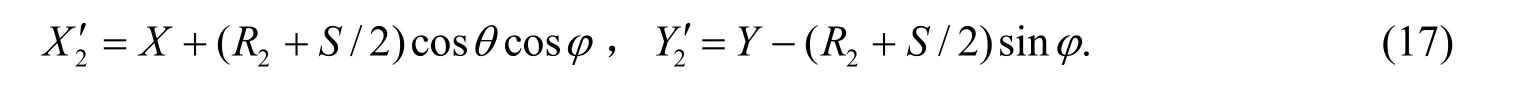
式(11)和(15)中的xmin，ymin分别由式(18)和(19)给出。

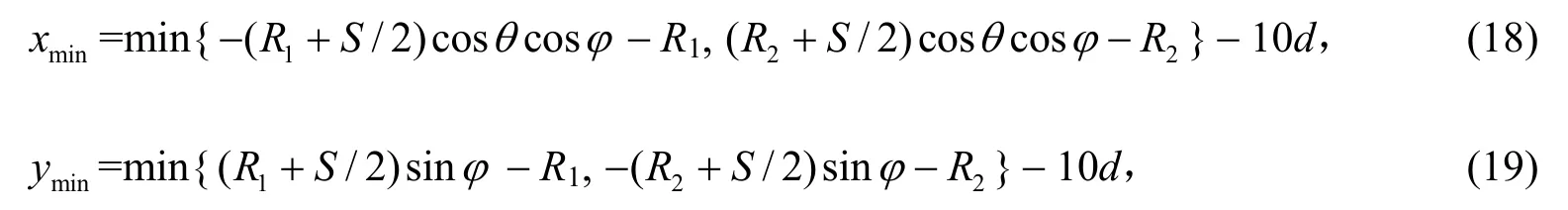
其中min{x，y}，表示取x 和y 中较小的数。

把式(11)和(15)相加得

式(20)为不考虑遮挡的双球激光后向二维散射强度像的计算公式。

1.4 考虑遮挡的双球激光后向二维散射强度像的计算公式

如果是凸体，根据本地入射角的大小可以判断凸体上的表面面元是否可以被激光照射到，如果本地入射角小于90°，面元被激光照射到，否则没有被照射到。双球作为一个整体，不是凸体，面元是否可照射到不能简单地通过本地入射角是否小于90°来判断。面元是否被照射到可以利用射线跟踪来判断，从本地入射角小于90°的面元沿着激光的后向方向发出一条射线，如果这条射线与另外1 个球相交，则面元被遮挡，不能被激光照射到，否则面元被照射到。本文的计算是在球的目标坐标系下进行。激光的入射方向沿着目标坐标系的Z 轴正向，设面元在目标坐标系的位置矢量（X0, Y0, Z0），则沿着激光入射方向反方向发出的射线上的点为（X0, Y0, Z0-l），代入式(6)得

如果式(21)中存在l>0 解，面元被另外1 个球遮挡。根据式(21)得

把不考虑遮挡的双球激光后向二维散射强度像的计算公式增加遮挡函数，得到考虑遮挡的双球激光后向二维散射强度像的计算公式，根据式(11)得

式(24)中 X1， Y1， Z1为

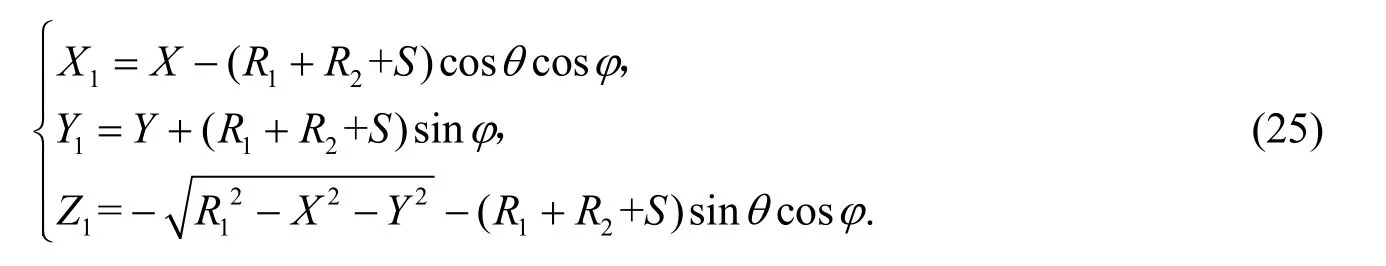
根据式(15)得

式(26)中的 X2， Y2， Z2为

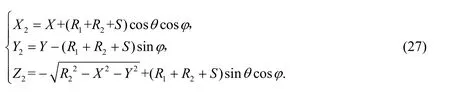
式(24)和(26)相加得

式(28)为考虑遮挡的双球激光后向二维散射强度像的计算公式。

2 朗伯双球的激光后向二维散射成像仿真的结果与讨论

根据双球激光后向二维散射强度像的计算公式，计算朗伯双球的激光后向二维散射成像的仿真结果，本文计算的球表面是朗伯表面， fr(β )是一个常数， fr(β )= kL。本文把朗伯双球激光后向二维散射成像仿真得到的图像称为朗伯双球的激光后向二维散射仿真图像。本文的计算是把计算图像的最大强度放大或缩小为255，其他的值等比例放大或缩小，计算时kL取值为0.1，计算结果与kL取值无关。

2.1 不考虑遮挡

2.1.1 θ 的影响

当R1，R2，S，φ，d 固定，θ 变化时双球的图像随着变化。R1=1 m，R2=2 m，S=1 m，d=10 mm，φ=0°，θ 从0°增加到180°，间隔30°，不考虑遮挡的朗伯双球的激光后向二维散射仿真图像如图1 所示。

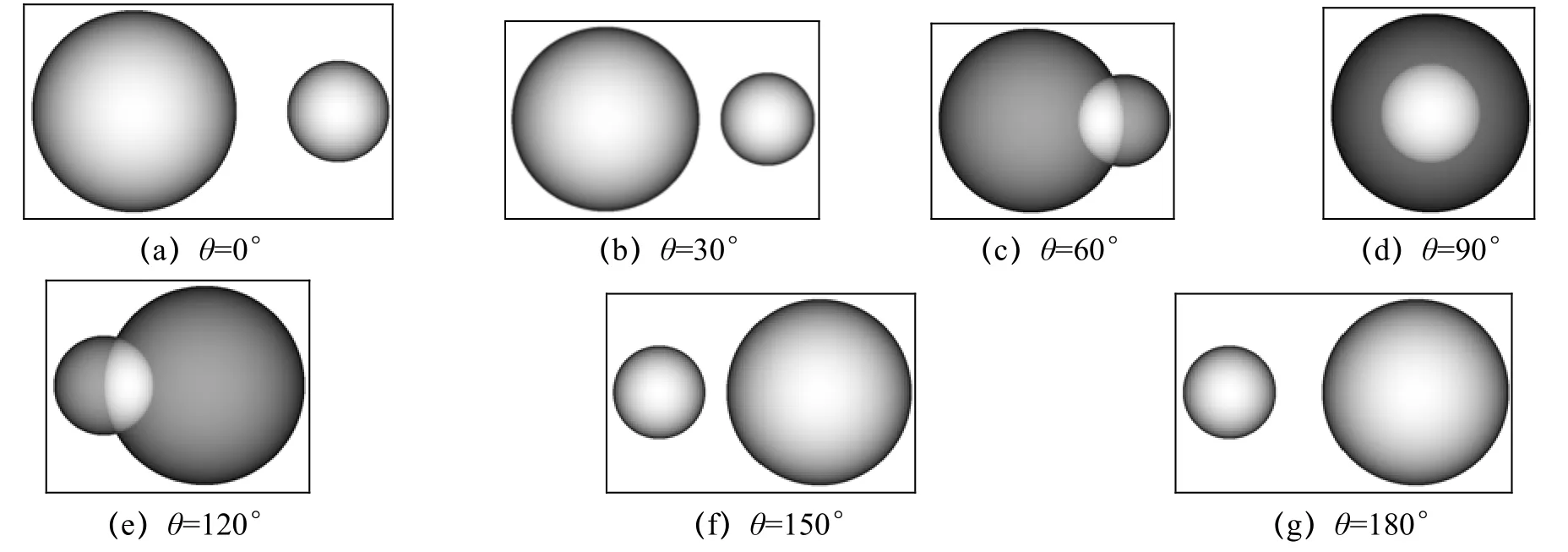
图1 不考虑遮挡的朗伯双球不同θ 的激光后向二维散射仿真图像（R1=1 m，R2=2 m，S=1 m，d=10 mm，φ=0°）

从图1 可以看出，随着θ 的变化，激光的入射方向发生变化，其成像结果有明显差异，图像能反映成像目标的各个方向的姿态特征。图1 中的（c），（d），（e）的图像存在很明显的重叠，是因为遮挡的部分也被计算到成像的结果里面，重叠部分计算出来的强度增加，这是因为遮挡部分不应该被累加到成像结果里，所以遮挡部分的位置成像强度增加。

2.1.2 φ 的影响

当R1，R2，S，θ，d 固定，φ 变化时双球的图像随着变化。R1=1 m，R2=2 m，S=1 m，d=10 mm，θ=0°，φ 从0°增加到180°，间隔30°，不考虑遮挡的朗伯双球的激光后向二维散射仿真图像如图2 所示。

图2 不考虑遮挡的朗伯双球不同φ 的激光后向二维散射仿真图像（R1=1 m，R2=2 m，S=1 m，d=10mm，θ=0°）

图2 中计算的图像，其中θ=0°，是沿着本地坐标系的Z 轴正向入射，从图2 可以看出，图2(b)～图2(g)是图2(a)的图像分别转动30°，60°，90°，120°，150°，180°。根据式(15)和式(17)，虽然入射的方向都是沿着本地坐标系的Z 轴正向入射，但计算结果是与φ 有关，所以图像有差别，但只是同一个图像的旋转。

2.2 考虑遮挡

2.2.1 θ 的影响

当R1，R2，S，φ，d 固定，θ 变化时双球的图像随着变化。R1=1 m，R2=2 m，S=1 m，d=10 mm，φ=0°，θ 从0°增加到180°，间隔30°，考虑遮挡的朗伯双球的激光后向二维散射仿真图像如图3 所示。

图3 考虑遮挡的朗伯双球不同θ 的激光后向二维散射仿真图像（R1=1 m，R2=2 m，S=1 m，d=10 mm，φ=0°）

图3 中（c），（d），（e）存在遮挡，通过和图1 中（c），（d），（e）图的对比，可以看出：考虑遮挡后，成像结果体现了遮挡的效果，成像更能体现出成像目标的特征，反应目标的真实成像特征。

2.2.2 φ 的影响

当R1，R2，S，θ，d 固定，φ 变化时双球的图像随着变化。R1=1 m，R2=2 m，S=1 m，d=10 mm，θ=0°，φ 从0°增加到180°，间隔30°，考虑遮挡的朗伯双球的激光后向二维散射仿真图像如图4 所示。

图4 考虑遮挡的朗伯双球不同φ 的激光后向二维散射仿真图像（R1=1 m，R2=2 m，S=1 m，d=10 mm，θ=0°）

图4 给出的图像是双球之间没有遮挡的情况，所以同图2 的结果是一致的。

3 结 语

本文研究朗伯双球激光后向二维散射成像仿真，推导成像计算公式，根据射线跟踪设计双球之间的遮挡剔除算法。本文一共建立4 个坐标系：本地坐标系、成像坐标系、2 个球的目标坐标系。分别在2 个球的目标坐标系下计算，本文只是分析了激光入射方向的影响，验证利用射线跟踪设计的遮挡剔除算法的正确性。