迁移学习下的火箭发动机参数异常检测策略

张晨曦，唐 曙，唐 珂

（1.中国科学技术大学计算机科学与技术学院，合肥 230000；2.中国文昌航天发射场指挥控制中心，海南文昌 571300；3.南方科技大学计算机科学与工程系，广东深圳 518000）

0 引言

火箭发动机是运载火箭的飞行动力核心，其组成复杂，工作环境恶劣，高频振荡、高温低温共存［1］，因此任何细小的异常在这样的条件下都易快速发展，极具破坏性，导致发射失败，带来巨大损失。在航天飞行史上，因发动机故障导致的失败次数超过总失败次数的50%［2］。因此，对发动机的异常检测可以帮助人们：1）在研制阶段发现设计或工艺的缺陷等潜在隐患；2）在测试阶段防止火箭带故障飞行，最大限度地规避发射风险；3）在飞行阶段挖掘发动机运行的异常和不足，为发动机性能优化改进提供反馈，提高航天装备试验鉴定能力。

目前工程应用中，常用的检测方法以红线法、专家系统法为主［3］，但随着大推力火箭、可回收等新技术的应用，火箭信息化和复杂度大幅提升，这些方法显露出了检测误差偏大、规则维护成本急剧增加、检测时效滞后等局限性。近几年来，得益于积累的海量数据，深度学习等新技术在不依赖专家知识的前提下将机器视觉、自然语言处理推向了工程化应用［4-6］。反观航天领域，火箭型号种类多，单型号尤其是新火箭样本有限，数据积累及共享困难，严重制约了目前主流机器学习技术在航天领域的应用。

对于航天领域这样的小样本领域，只依靠领域专家，难以快速形成评估能力，只依靠数据又缺乏大规模用于表征学习的数据集。因此本文的研究动机就是结合专家知识和数据驱动来解决传统方法的不足，具体是以发动机为研究对象，通过领域知识构建特征空间，利用迁移学习来处理样本规模有限导致的评估模型性能低问题。本文针对YF-75 和YF-77 液体发动机飞行任务数据，进行预处理后构建特征空间，选择k最近邻（k-Nearest Neighbors，kNN）与支持向量机（Support Vector Machine，SVM）两种分类模型验证了实例迁移、模型迁移方法对YF-77发动机参数异常检测模型训练和优化的有效性。

1 背景及现状

1.1 火箭发动机参数评估内容

火箭发动机包括涡轮泵、燃烧室等部件，每个部件上安装有不同传感器，分别测量不同的指标（如温度、压力、流量），业内通常称为遥测参数（或参数），通常一次飞行任务中与发动机有关的参数个数在2 000～2 500。

发动机工作主要有三种过程（或状态），分别为启动、额定工作（或满工况）和关机过程。图1 展示了三种过程的异常检测步骤。

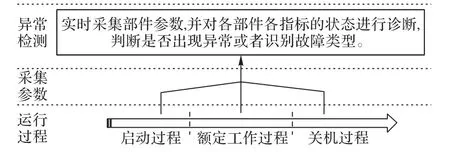
图1 在各个过程检测发动机参数状态Fig.1 Checking engine parameter status in different processes

其中启动、关机过程是十分复杂的瞬变过程，短时间内大量参数会发生剧烈变化，实践表明发动机的大部分故障都发生在这样的瞬变过程［7］。三类过程都有固有的关键指标来描述其状态，以氧泵转速的启动过程为例，表1 展示了其关键指标、物理意义及指标异常的潜在典型故障模式。

表1 氧泵转速启动过程的关键指标Tab.1 Key indicators of oxygen pump speed in startup

1.2 参数异常检测方法现状

红线法、专家系统和机器学习是火箭参数异常检测中常用的三类方法：

1）红线法包括阈值法和包络法，前者是不带时间维的理论常量区间；后者根据历史正常数据生成带时间维度的包络上下限。

2）专家系统，是由火箭领域专家通过领域知识和经验得到的状态判决规则［8］。

3）国内从20 世纪90 年代开始至今，先后应用SVM、神经网络和时间序列分析等方法开展对发动机故障检测与诊断的研究［9-10］。

以上方法都有着各自的特点和适用情况。阈值法丢失了时间维，常用于检测当前时刻的状态，且精度不高［11］；包络法则受样本规模和方法本身的制约，假阳性和假阴性现象严重。红线法还对噪声敏感，难以适用于参数规模大或者样本少等情况，检测误差一般较大：如果误判会加重人工筛选的负担，提高了人力成本；如果漏判则降低了方法可信度，增加了飞行风险。

专家系统则受制于专家知识，发动机系统覆盖学科领域广泛，知识表述困难。规则建立过程复杂耗时，规则质量受专家能力和经验制约；规则对技术状态变化敏感，导致了专家规则更新维护代价高昂。

机器学习方法则主要受制于样本规模和质量［11］，航天领域单型号尤其新型发动机的样本较少，而且数据的采集、分类和处理标准也不够规范统一，导致预处理难度大，这些都严重阻碍了大规模的表征学习和模型训练［2］。

2 基于迁移学习的参数异常检测

迁移学习的目的就是设法将相近或相似领域的数据、知识等信息实现共用，一般将迁移信息的来源称为迁移领域，将迁移信息的去向称为目标领域，来解决目标领域样本规模不足给模型训练带来的制约，从而有效解决小样本领域应用机器学习的困境［11-14］。按照迁移的信息内容可以分为实例迁移、特征迁移、模型迁移、关系迁移［11］。目前迁移学习的有效性已经在图像检索、语音识别、文本分类和语义分析等领域得到充分的验证［15-17］，在航天领域应用还处于起步阶段。

YF-77 液体火箭发动机作为新型发动机，样本规模太少，异常检测分类模型无法进行有效的训练，因此本文引入成熟型号YF-75发动机的样本数据和其异常检测模型等信息迁移到YF-77领域，实现发动机参数异常检测，以完成火箭飞行阶段的状态监测，为指挥决策和故障诊断提供辅助的支撑信息。

在具体迁移的实践中，将面临如下问题：

1）YF-75与YF-77两型发动机的相似性；

2）如何处理两个领域之间的差异；

3）如何构建有效的特征向量；

4）选择恰当的机器学习分类模型；

5）使用何种迁移方法。

本文将分别在2.1、2.2、2.3、2.4、3.1 节详细论述以上问题。

2.1 两型发动机的相似性分析

为面向现实应用需求，本文以YF-75 和YF-77 型液体发动机分别作为迁移领域和目标领域，其中YF-75 型发动机执行任务次数较多，共有352 个样本；而YF-77 是近年研制成熟的新型发动机，目前仅有24个样本。

根据这两型发动机的设计原理，它们都属于氢氧发动机，燃烧方式都是燃气发生器循环，并且具有相同的分系统构造，主要性能如比冲、推进剂混合比等相近，二者的共有参数占YF-77 所有参数的58%，其中关键参数更是高达73%，且这些参数在启动、额定工作和关机三个过程中具有相同的变化趋势，只是在具体数值上有差别。

以氧泵转速为例，它是专家评估发动机状态时首要关注的参数之一，并常使用｛启动时长，最终稳定值，（最终稳定值-起始数据值）/相应时间差，相邻数据点斜率之平均值，相邻数据点斜率之标准差｝五个特征值作为评价泵转速的主要依据，记为｛T，R，d（R），E（d），S（d）｝。其样本已经基于专家系统对其进行正常与异常的二分类标注，表2展示了两型发动机五个特征值在正常和异常下的区间变化情况（数据经变换已脱密）。

计算两发动机之间各特征值正常样本区间的左边界数值的差距除以两个左边界数值的平均值依次是17.74%、1.85%、6.62%、4.41%、17.16%，右边界依次是2.11%、0.66%、1.07%、3.89%、12.40%；二者异常样本区间的分布都明显异于正常样本，且各特征值异常样本区间的左边界差距除以两个左边界数值的平均值依次是9.22%、23.92%、11.35%、5.96%、20.56%，右边界依次是6.90%、0.40%、5.47%、11.99%、7.92%。从原理、构造和数据统计的角度都说明了两型发动机的相似性，本文还将在第3 章的实验中充分验证迁移的有效性。

表2 YF-75和YF-77氧泵转速正常、异常样本数值区间Tab.2 Value ranges of normal and abnormal samples of oxygen pump speed in YF-75 and YF-77

2.2 针对数据差异进行预处理

2.2.1 时间对齐

不同任务中各发动机的T0（发动机点火启动的时刻）是互不相同的，为了保证各时间序列的开始时刻对齐，需要将启动过程样本中所有时间记录值都减去对应的T0，使得每个样本都以0 s为开始。

2.2.2 数据归一化

相同类型参数在不同发动机中，其设计额定工作值可能存在差异；即使在同型号发动机的不同飞行任务中，其实际额定工作值也不完全一致。为了关注变化趋势，本研究对每段数据样本进行归一化处理：对同一型号发动机，首先筛选所有启动过程正常的参数样本，去除噪声后，获取其中各样本的最大值和最小值，分别记为MAXrated和MINrated；然后以“MINrated值转换为0，MAXrated值转换为1”作为缩放标准，预处理所有样本（包括正常和异常）启动过程的时间序列值，例如对于任意value值，它将被归一化为：

2.3 特征空间构建

本文希望找到恰当的特征向量，它既能区分正常与异常样本的特征，又能同时刻画出该参数在不同领域的变化趋势。

2.3.1 特征对正常与异常的区分性

国内研究人员曾对氢氧发动机的故障模式做出分类和仿真［1］，从已有故障模式中总结出与氧泵转速有关的6种典型异常表征，如表3 所示，同时基于领域知识将异常表征现象与表1 中启动过程发动关键指标、专家系统的五个特征值做出关联对应。

以YF-75 型发动机氧泵转速为例，针对每一类异常表征取一个异常样本，同时取一个正常样本作对比，如图2所示。

图2 YF-75型启动过程氧泵转速正常样本与异常样本之间的时间序列数据曲线对比Fig.2 Curve comparison of time series data of normal and abnormal samples of oxygen pump speed during YF-75 startup

为进一步验证专家常用的5 个特征值的有效性，本研究在此基础上，再添加｛平均值，最大值，最小值，（最大值-最小值）/相应时间差，标准差｝这些常见的统计特征，分别记作｛E，Max，Min，d（M），S｝，共组成一个10 维向量，然后进行偏最小二乘回归（Partial Least Squares Regression，PLSR）分析，如图3所示，得到不同特征与样本标注的相关性。

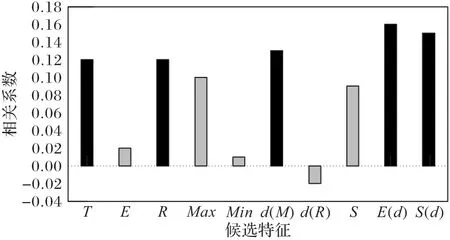
图3 YF-75发动机氧泵转速的PLSR结果Fig.3 PLSR results of YF-75 oxygen pump speed

表3 典型的异常表征现象及对应的启动关键指标和专家特征值Tab.3 Classic abnormal representation phenomena and corresponding key indicators，expert feature values

可以看出，对于氧泵转速而言，｛T，R，d（R），E（d），S（d）｝确实与标注结果的相关性更大；因此该特征向量满足了物理意义和统一意义上的解释，能够区分正常与异常样本的不同。

2.3.2 刻画两个领域的趋势

目前仍需明确该特征向量是否能够较好地同时刻画出该参数在不同领域的变化趋势，从而确定这一特征向量在迁移过程中能否有效发挥作用。首先由表2可以看出，在YF-75和YF-77 发动机氧泵转速样本集之间，用该特征向量表示的正常样本区间是相似的，异常样本区间也是相似的。

而除了这些领域专业知识和统计信息，本研究通过第3章设计的迁移实验来验证：如果有迁移的机器学习方法优于无迁移的机器学习方法，则可以说明这个特征向量能够刻画两个领域的变化趋势并有效地用于迁移学习中。

2.4 异常检测分类模型

迁移学习的目的是解决传统机器学习在小样本领域的性能，因此依然需要选择合适的机器学习算法，基于已有的研究［1，9］，本文选用的是kNN和SVM算法。

2.4.1kNN分类模型

kNN算法的步骤如下所示：

输入：特征向量表示的氧泵转速训练样本集、测试样本集；

输出：测试样本集的kNN分类结果正确率。

1）对某测试样本，计算与各训练样本的距离，按距离从小到大进行排序；

2）选取距离最小的k个训练样本（本文实验中取k=3）；

3）确定前k个训练样本中，两个类别的出现频率；

4）将出现频率最高的类别作为该测试样本分类结果；

5）重复步骤1）～4），得到测试集的所有分类结果，与已有标注比对计算正确率。

其中kNN 算法里的距离度量使用的是标准化欧氏距离，设样本1 的特征向量为A=（a1，a2，a3，a4，a5），样本2 的特征向量为B=（b1，b2，b3，b4，b5），si是样本集的第i维特征值的标准差，其二者距离d(A，B)计算公式如下：

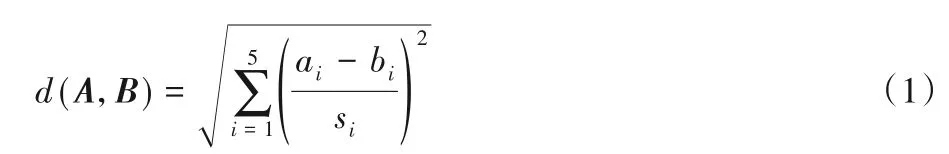
2.4.2 SVM分类模型

SVM算法的步骤如下所示：

输入：特征向量表示的氧泵转速训练样本集、测试样本集；

输出：测试样本集的SVM分类结果正确率。

1）构建SVM优化函数；

2）使用SMO 算法基于训练集求解SVM 模型的二分类分界面参数；

3）对某测试样本，通过已建立模型计算得到分类值；

4）如果分类值大于0，则判定该测试样本属于第1 类，否则属于第二类；

5）重复步骤3）～4），得到测试集所有分类结果，与标注并比对计算正确率。

设训练样本数量为n，特征矩阵为X=（x1，x2，…，xn），标签向量为Y=（y1，y2，…，yn），求解满足式（2）中优化函数的W和b，即可得到SVM的超分类平面XTW+b=0。

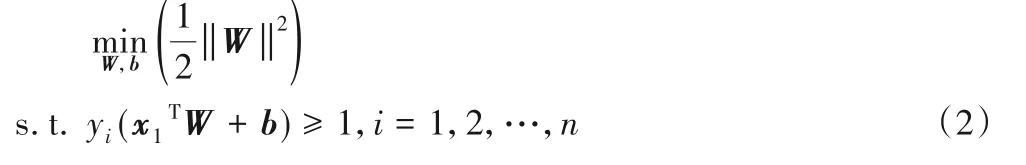
3 实验及分析

3.1 实验设置

待研究对象是YF-77 型发动机氧泵转速，其样本规模较小，是目标领域；迁移领域是YF-75 型发动机氧泵转速样本集，其规模较大。首先以传统的包络法为比较对象，验证kNN和SVM（本文使用的训练集与测试集均为噪声较大的飞行实战数据，复现的SVM 实验精度略低于文献［9］中采用仿真和试车数据的结果）算法在大样本数据集中确实有优于包络法的表现，见对照实验1 和2；然后观察这两个算法在小样本领域是否优于包络法，见对照实验3和4，如果并不优于，再使用迁移方法，观测实验5和6对比迁移是否有效。

在具体的迁移方法上，本文使用了基于实例、基于模型的迁移，其流程如图4所示。实例迁移是将YF-75发动机氧泵转速的样本实例作为信息，在YF-77 模型建立前作为异常检测分类模型的数据输入；模型迁移是将YF-75 已经建立好的异常检测分类模型作为信息，传递给YF-77领域使用；最终都需要通过测试集对比结果计算性能。

图4 基于实例和基于模型的迁移学习流程Fig.4 Flowcharts of transfer learning based on instance and transfer learning based on model

图5 直观地展示了实验设置与流程，表4 和表5 详细介绍了各实验组的内容。为了通过对比检验迁移策略的有效性，需要设定能够合理评价模型异常检测性能的标准。

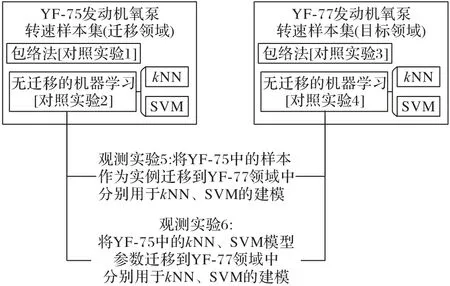
图5 实验设置与流程Fig.5 Experimental setting and process

为了更完备地发现所有异常状态，希望评估系统首先尽量不遗漏任何可能的异常，同时不应随意提示异常，否则会导致下一步耗费大量人工筛选成本。因此实验以漏报率（Missing_Alarm）和误报率（False_Alarm）作为“异常状态筛选性能”的评判指标。

假设有NN个类别为Normal（正常）的样本被分类为Normal，有AN个类别为Normal 的样本被分类为Abnormal；有AA个类别为Abnormal（异常）的样本被分类为Abnormal，有NA个类别为Abnormal的样本被分类为Normal，漏报率和误报率的计算公式分别如下：

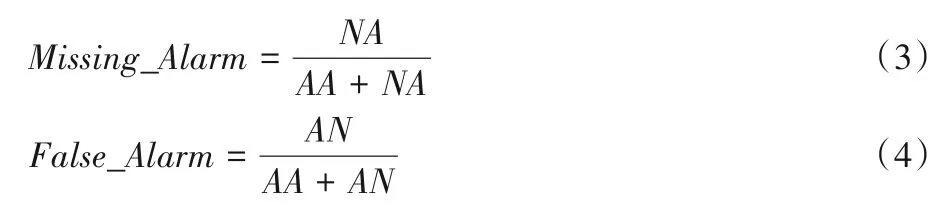
漏报率计算多少异常样本被模型遗漏，误报率关注多少正常样本被模型误认为异常。理想情况下，这两个指标都等于零，但实际中二者是很难同时降低的，漏报率的降低一般带来误报率的增长，误报率的降低往往导致漏报率的增长。综上，对于火箭发动机而言，一个好的参数异常检测系统，应首先满足低漏报率，再尽量满足低误报率。

表4 包络法与无迁移机器学习在不同规模数据集上的实验设置对比Tab.4 Experimental setting comparison of envelope method and traditional machine learning on different scale datasets

表5 包络法、无迁移机器学习和迁移学习在目标领域上的实验设置对比Tab.5 Experimental setting comparison of envelope method，traditional machine learning and transfer learning in target domain

3.2 结果分析

实验结果如表6 和表7 所示，通过观察对比，由表6 可得到：

1）在包络法中，当数据量增多时，误报率会降低，但漏报率会增长，说明随着标注正常样本的增多，包络上限会升高，包络下限会降低，导致可能更多的异常样本被包络涵盖。

2）当数据规模较大时，无迁移kNN、SVM 方法的漏报率（10.23%、12.50%）、误报率（9.97%、9.31%），分别低于包络法的漏报率（59.09%）、误报率（26.88%），说明提取的特征向量可以较好体现正常样本与异常样本的区别。

3）当数据规模较小时，无迁移kNN、SVM 方法的漏报率（58.33%、41.67%）和误报率（41.67%、60.83%），都比数据规模较大时相应地要高，说明无迁移的kNN、SVM方法受制于数据规模，当数据集较小时难以发挥效果。

4）即使表现最好的对照实验2，依然存在漏报和误报的样本，观察每次kNN、SVM 的漏报和误报样本，都处在决策边界附近，说明当前提取的特征未能完美区分出一些特殊样本，后续实验可以尝试通过修改特征权重调整决策边界。

由表7可以得到：

5）观测实验5 的漏报率（14.00%、18.00%）和观测实验6的漏报率（12.50%、25.00%），都低于对照实验3、4 漏报率的最小值（33.33%）；观测实验5 的误报率（17.68%、13.53%）和观测实验6的误报率（22.22%、14.29%），都低于对照实验3、4误报率的最小值（41.67%）；说明基于实例和基于模型的迁移策略都能提高kNN、SVM模型的分类性能。

6）两个迁移学习组的漏报率和误报率都略高于YF-75 的无迁移机器学习组，且基于实例的kNN 和SVM 表现略优于基于模型的相应方法。对于模型迁移而言，可能是没有调整参数，下一步可以比较调整不同参数对模型迁移的影响；对于实例迁移而言，原因可能是目标领域和迁移领域样本使用的是相同权重，下一步可以比较调整不同权重对实例迁移的影响。

7）观测实验5和6同样存在漏报和误报的样本，其原因可能包括特征权重，以及迁移过程中的样本权重或者模型参数。

表6 包络法与无迁移机器学习在不同规模数据集上的实验结果对比Tab.6 Experimental result comparison of envelope method and traditional machine learning on different scale datasets

表7 包络法、无迁移机器学习和迁移学习在目标领域上的对比实验结果Tab.7 Experimental result comparison of envelope method，traditional machine learning and transfer learning in target domain

3.3 结论

由实验结果分析可以得出结论：

1）包络法在不同量级样本的领域中都具有局限性；

2）无迁移的机器学习方法适合大样本集的参数异常检测，而在小样本领域具有局限性；

3）在数据量较少的YF-77 型发动机小样本领域，经过时间对齐、数据归一化得到样本，经过特征空间构建得到特征向量后，使用基于实例迁移的kNN、SVM机器学习方法对氧泵转速建立分类模型，在测试集的漏报率相比无迁移的kNN、SVM分别降低了44.33 个百分点、23.67 个百分点，平均34.00 个百分点，误报率分别降低了23.99个百分点、47.30个百分点，平均35.64 个百分点；使用基于模型迁移的kNN、SVM 建立的模型，在测试集的漏报率相比无迁移的kNN、SVM分别降低了45.83 个百分点、16.67 个百分点，平均31.25 个百分点，误报率分别降低了19.45 个百分点、46.54 个百分点，平均32.99个百分点。图6 使用直方图更加直观展示了实验结果，两种迁移方法都比相应无迁移的方法，在漏报率和误报率上降低了30个以上的百分点，模型性能得到较显著的提升。

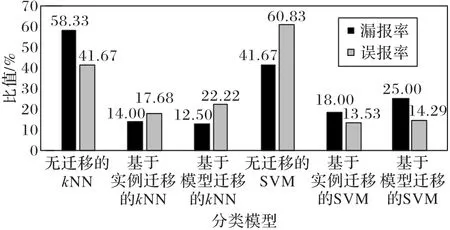
图6 无迁移、基于迁移的分类模型漏报率和误报率Fig.6 Missing and false alarm rates of classification models without and based on transfer

4 结语

本文探索了YF-75 与YF-77 两型氢氧发动机之间的共性知识及可迁移性，通过构建合适的特征空间，采用实例迁移和模型迁移的方法，以YF-75、YF-77 型发动机启动过程氧泵转速数据集为例，通过设置四组实验有效验证了相比包络法和无迁移对照，迁移对照组的kNN、SVM分类器在异常检测的精度上得到极大提高。

虽然验证了迁移的有效性，但仍存在如下问题亟待解决：

1）目前只关注单个参数的异常检测，而没有对发动机的状态进行评估，发动机状态是由多个参数联合决定的，因此需要采用分层的方式提取特征，下一步将尝试在迁移的前提下利用神经网络来解决这一问题。

2）不同参数之间存在各类关联，例如因果、并发、冗余关系，下一步试图通过关联规则挖掘来获得参数间的关联关系，进一步从数据的角度去发掘发动机技术特点。

3）迁移的内容还包括特征向量、特征权重、参数权重、参数关系等，下一步将研究特征、关系的迁移学习对目标领域的建模影响。