基于启发式搜索的浮点表达式设计空间探索方法

李 钊，董霄霄，黄程程，任崇广

（山东理工大学计算机科学与技术学院，山东淄博 255000）

0 引言

随着信号处理和图像处理等在现场可编程门阵列（Field Programmable Gate Array，FPGA）上的广泛应用，浮点计算在FPGA 上的应用变得越来越流行［1-4］。浮点数可以增加数据的表示范围，但是浮点计算的误差也会导致最终结果不准确。根据IEEE 754 标准，通过加、减或乘两个浮点数产生的计算结果都应四舍五入为IEEE 754 浮点数格式，这种舍入是浮点计算不准确的原因。当浮点数格式固定的前提下，浮点计算的误差主要取决于浮点表达式的形式。例如：表达式(x+y)2可表示为(x+y)×(x+y)和x×(x+y)+y×(x+y)等不同的形式，当x的取值范围为[0，0.000 02]，y的取值范围为[20，21]时，两个表达式的表示范围分别为[-5.53×10-5，5.53×10-5]和[-5.05×10-5，5.05×10-5]，从而产生不同的误差［5］。

浮点计算在FPGA 平台上实现时，若浮点数格式固定，资源消耗主要取决于浮点表达式的形式。例如：表达式(x+y)×(x+y)需要一个乘法器和两个加法器，而表达式x(x+y)+y(x+y)需要两个乘法器和三个加法器，表达式(x+y)×(x+y)消耗更少的资源。因此通过优化浮点表达式的结构，可实现资源消耗的优化。

浮点计算还需考虑计算时间，计算时间主要依赖于浮点运算器的流水线深度以及浮点表达式的形式。当浮点运算器确定的前提下，可以通过改变浮点表达式的形式来改变计算时间。例如：若采用相同的浮点运算器，表达式(x+y)×(x+y)可设计两级流水线结构完成计算，而表达式x(x+y)+y(x+y)需要设计三级流水线结构完成计算，表达式(x+y)×(x+y)具有更短的计算时间。

一个浮点表达式经过因式分解和提取公因数等方法进行变形后可生成大量等价的浮点表达式，例如：x2+xz+z(x+y+z)+y(2x+y+z)可产生698 个等价表达式，每个表达式具有不同的计算精度，而且资源消耗和计算时间也不同。可采用浮点运算器的结构优化、指数和尾数位宽调节和等价表达式的设计空间探索等方法，实现浮点计算在FPGA 上的优化。

文献［6］中采用半单元偏置格式设计浮点加法器和乘法器，以降低浮点运算器的资源消耗并提高计算速度。文献［7］中提出了一种新的位对重编码算法，该算法可有效减少浮点乘法运算中部分积行数，并减少与多路复用器、移位器和加法器相关联的部分积的数量，与全精度乘法器相比可节省49%的面积和44.2%的功耗。文献［8］中采用Newton-Raphson 迭代方法设计了一种32 位流水线浮点除法器，该除法器支持IEEE 754 标准中指定的所有类型的数据，该方案与现有方法相比需要多消耗30%的功耗，但所提出的流水线方法显著降低了计算时间。文献［5］中提出OptiFEX 优化框架，可根据数据输入范围和最大允许误差等参数，调节浮点运算器指数和尾数的位宽，从而减少资源消耗，提高计算效率。

对浮点运算器进行优化，可减少运算器的资源消耗，并有效提高计算效率，但是浮点计算多为多个浮点数的混合运算，浮点表达式的结构也是制约浮点计算优化的关键。

文献［9］中设置一组关于资源消耗、计算时间和精度的约束条件，并从等价表达式集合中选择满足约束的等价表达式，从而完成设计空间的探索。利用该方法选择的表达式虽然满足约束条件，但仍可能是可支配的，因此选择的表达式不一定是最优表达式。文献［10］中通过迭代分解的方法对初始浮点表达式进行变形，在迭代过程中采用Pareto 算法删除非最优的表达式，从而减少等价表达式的数量，然后从剩余表达式中选择资源消耗和计算时间最优的浮点表达式。该方法在探索过程中对可支配等价表达式及其后继表达式进行了删减，其探索过程不能覆盖整个搜索空间，因此其选择的非支配表达式的资源消耗、计算时间和精度等性能可能不是最优的。

针对上述问题，本文提出一种新的浮点表达式设计空间探索的方法，该方法不仅对非支配表达式的邻域进行空间探索，同时对可支配列表中的表达式进行再次评估，选择该列表中非支配表达式，并对其邻域进行探索，最后再次对非支配列表中的等价表达式进行探索，得到最优的浮点表达式。该方法可对给定的浮点表达式及其等价表达式进行探索，探索过程基本覆盖整个搜索空间，根据优化目标和约束条件选择最优的等价表达式，因此不会引入浮点数处理的错误；同时该方法有效提高了非支配列表中非支配表达式的多样性和随机性，提高了最优表达式的性能指标。

1 产生等价表达式的方法

浮点表达式在等价变换过程中，以不同的等价表达式为起点，可能会重复出现同一个表达式，如图1 中，表达式x(x+y)+y(x+y)重复出现两次。若多次对同一个表达式进行性能评估会影响空间探索的效率。

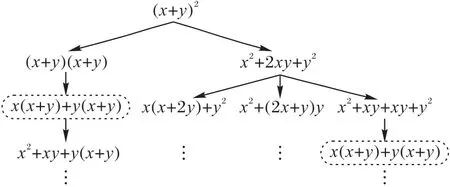
图1 浮点表达式变换示例Fig.1 Example for floating-point expression transformation

本文参考文献［5］中的方法实现了等价表达式的变换。首先对初始表达式进行因式分解，直到表达式不能进一步分解，然后对分解后的表达式进行迭代提取公因式，直到没有新的等价表达式产生。例如对(x+y)2的变换过程如图2 所示，采用该方法可有效避免在等价变换过程中重复出现同一表达式。

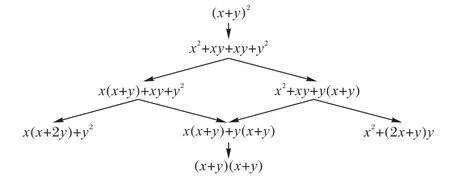
图2 （x+y）2的等价变换过程Fig.2 Equivalent transformation process of（x+y）2

2 设计空间探索方法

设计空间探索是一个多目标优化过程，可实现多目标的折中［11-13］。为了提高设计空间探索的效率，需要根据优化目标，设计目标函数以及相关约束，并在设计空间探索过程中对每个设计个体的性能进行评估，判断是否满足目标函数。另外需要设计搜索算法，利用该算法选择下一步要评估的个体，将设计空间引导到符合优化目标的区域。

2.1 优化目标函数

浮点表达式在设计空间探索过程中，会产生多个等价的表达式，表达式的精度、计算时间以及资源消耗等都会有所不同。设计空间探索的目的是依据优化目标，将设计空间引导到符合优化目标的区域。浮点表达式设计空间探索的优化目标函数如式（1）：

其中：P为浮点表达式的计算精度，可由式（2）计算得到，为表达式以更高指数和尾数长度表示的计算结果Fr(xr1，xr2，…，xrn)与当前参与空间探索的表达式的计算结果Ff(xf1，xf2，…，xfn)之差的绝对值，其值越小表示计算精度越高，例如当前参与计算的为IEEE754 标准的32 位浮点数，则采用IEEE754标准的64位浮点数作为参考数据。D为浮点表达式在FPGA 上实现后从输入浮点数据到输出计算结果的时间，由关键路径上各处理单元的计算时间之和计算得到，如式（3）所示，m为关键路径上处理单元的数量。R为FPGA 上实现浮点计算的资源消耗，由各个处理单元的资源消耗之和计算得到，如式（4）所示，t为浮点运算所需处理单元的数量。为了更好地实现多目标优化，对优化目标函数设置了多个约束条件，参考表达式的参数xri和参与计算表达式的参数xfi的取值必须在其允许的取值范围内，关键路径的计算时间Dkp应该大于等于任意处理单元的完成时间Dend(k)，任意处理单元的完成时间Dend(k)可由该处理单元的计算时间与该处理单元的前任处理单元的计算时间之和得到，如式（5）所示，其中d为前任处理单元的数量。最后浮点运算的资源消耗应小于等于FPGA平台总的资源Rtotal。

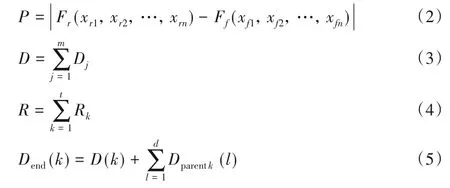
2.2 启发式搜索方法

浮点表达式在设计空间探索中会产生多个等价表达式，等价表达式之间的计算精度、资源消耗和计算时间等都有所不同［14-15］。每次迭代过程中采用启发式搜索方法对产生的浮点表达式进行评估，提取非支配的浮点表达式作为局部最优的表达式，并以非支配表达式为起点进行新一轮的迭代。

2.2.1 非支配浮点表达式的定义

若e为一个浮点表达式，N为浮点表达式的集合，且e∈N，若e满足式（6），则浮点表达式e为集合N中的非支配浮点表达式。

其中：∀x∈N；Precision、Delay和Resource分别为表达式的计算精度、计算时间和资源消耗。

2.2.2 非支配浮点表达式的选择

现有的方法在进行空间探索时，为了提高探索效率，直接删除可支配表达式的后继等价表达式，不对其进行评估，而后继表达式中可能存在非支配解。为此，本文提出一种新的非支配浮点表达式的选择方法，可覆盖整个探索空间，算法流程如图3所示。

1）首先将给定的需要探索的表达式进行因式分解，将分解后的表达式作为初始表达式。

2）然后对该表达式提取公因式进行等价变形，即得到初始表达式的邻域，并计算邻域中等价表达式的计算精度、计算时间和资源消耗等性能指标，得到非支配的等价表达式和可支配的等价表达式，并将可支配的表达式添加到可支配列表中，同时保存非支配表达式到非支配列表中。

3）以新的非支配表达式为起点，通过提取公因式得到相应的邻域，并探索邻域，最终得到该起点邻域中的非支配的等价表达式和可支配的等价表达式，并分别添加到可支配列表和非支配列表中。

4）再次以新的非支配表达式为起点，按照步骤3）进行探索，直到达到规定的迭代次数或者无新的等价表达式产生。

5）上述过程未对可支配表达式的邻域进行探索，该步骤首先对可支配列表中的表达式进行探索，提取该集合中的非支配表达式，并对其邻域进行探索，将邻域中的非支配表达式保存到非支配列表中，可提高非支配列表中多项式的随机性和多样性。

6）由于非支配列表中的表达式是在相应的邻域内是非支配的，因此需要再次对非支配列表中的等价表达式进行探索，若该列表中存在可支配的表达式，则将其删除，保留的等价表达式即为最终的最优浮点表达式。

图3 浮点表达式空间探索算法流程Fig.3 Flowchart of floating-point expression space exploration

3 实验验证

为了验证本文提出的基于启发搜索的浮点表达式设计空间探索方法的有效性，将提出的空间探索方法与现有的针对浮点表达式空间探索的方法从计算精度、计算时间和资源消耗等方面进行对比分析。为了便于比较，选择表达式结构由简单到复杂的多个浮点表达式作为测试表达式，表达式中各参数的精度设定为：x∈[0.01，0.15]，y∈[0.32，0.43]，z∈[1.11，1.35]，指数的宽度设为5，尾数的宽度设为10，采用就近舍入方法。

为了更好地对计算精度进行评估，分别在设定的精度范围内，均匀地取10 个浮点数据，首先分别按照IEEE754 标准格式对表达式进行计算，将该计算结果的均值作为参考的准确结果，然后按照实验要求格式，对表达式进行计算，并计算实际结果的平均值，两个平均值之差的绝对值即为计算精度。在设计空间探索过程中，利用FloPoCo［16］来提取加法器和乘法器的资源消耗和计算时间。FloPoCo 是一个用于生成算术数据通路的开源C++框架，其输出是一个可综合的VHDL代码。

为了对各种设计空间探索方法的计算时间和资源消耗进行定性和直观比较，分别从各种方法产生的非支配表达式集合中随机选择5个表达式在FPGA 平台上进行仿真实验验证。FPGA 平台选用Kintex7 系列的XC7K325T，综合工具为Vivado2017.4，参考时钟频率为120 MHz。

实验选择3 个主流的浮点表达式设计空间探索方法进行对比分析，包括快速选择空间探索（Fast Selection Design Space Exploration，FSDSE）方法［10］、基于迭代分解的空间探索（Design Space Exploration using Iterative Factorization，DSEIF）方法［9］和调节浮点运算器指数和尾数位宽自动调节的设计空间探索（Exploring Area-efficient with Optimized Exponent/mantissa Widths，EAOEW）方法［5］。

3.1 计算精度对比分析

表1 为不同的设计空间探索方法对不同表达式进行探索后，选择的非支配表达式计算产生的计算精度对比。由表1可知，本文提出的浮点表达式设计空间探索方法的计算精度与DSEIF 方法相当，但是要优于FSDSE 和EAOEW 方法。例如针对浮点表达式(x+y+z)2，本文提出的方法的计算精度等于DSEIF 方法的计算精度，与EAOEW 方法相比本文提出方法的计算精度提高了9%，与FSDSE 方法相比提高了4%。主要原因在于DSEIF 方法是对整个搜索空间进行探索，分别对每个等价多项式进行计算精度等性能进行评估，并从中选择非支配表达式，其缺点是空间探索效率低。FSDSE 为快速选择空间探索方法，在探索过程中对可支配等价表达式及其后继表达式进行了删减，其探索过程不能覆盖整个搜索空间，而可支配表达式的后继节点中可能存在计算精度更高的表达式，因此其选择的非支配表达式的计算精度会降低。EAOEW方法在空间探索过程中，只对资源消耗进行评估，所以其计算精度最低。本文提出的方法采用启发式搜索，在避免对可支配表达式进行探索的同时，尽可能地覆盖整个搜索空间，提高了最终选择非支配表达式的多样性和随机性，从而保证了计算精度的准确性。

表1 四种方法的计算精度对比Tab.1 Calculation accuracy comparison of four methods

3.2 计算时间对比分析

图4 为针对每个测试表达式随机选择的5 个最优等价表达式计算时间的平均值。计算时间为将经过设计空间探索后得到的最优表达式在FPGA 平台上运行所需要的时间。从图4 中可知，本文提出的空间探索方法得到的非支配表达式的计算时间与DSEIF 方法相当，要优于FSDSE 和EAOEW 方法，例如针对表达式x(x+2z)+y(y+2x)+z(z+2y)，与FSDSE方法相比本文提出方法的计算时间减少了5%，与EAOEW 方法相比减少了12%，本文方法可选择计算时间更优的等价表达式。主要原因在于本文方法不仅对非支配表达式的邻域进行探索，同时选择可支配列表中的非支配表达式，并对其邻域进行探索；还对最终产生的非支配列表再次进行探索，最终得到最优的等价表达式，从而提高了选择计算时间最优的表达式的概率。

图4 四种方法的计算时间对比Fig.4 Calculation time comparison of four methods

3.3 资源消耗对比分析

图5 为针对每个测试表达式随机选择的5 个等价表达式资源消耗的平均值。从图5 中可知，与计算时间不同，EAOEW 方法具有最优的资源消耗，本文提出的空间探索方法得到的非支配表达式的资源消耗与DSEIF 方法相当，要优于FSDSE 方法，例如针对表达式y(x+y)2，与FSDSE 方法相比，本文提出方法的资源消耗减少了5%。主要原因是：在设计空间探索过程中，EAOEW 只针对资源消耗一个性能进行评估，选择的等价表达式是资源消耗最优的；而本文方法是针对计算精度、计算时间与资源消耗三个性能进行综合评估的，为三个性能的折中优化。

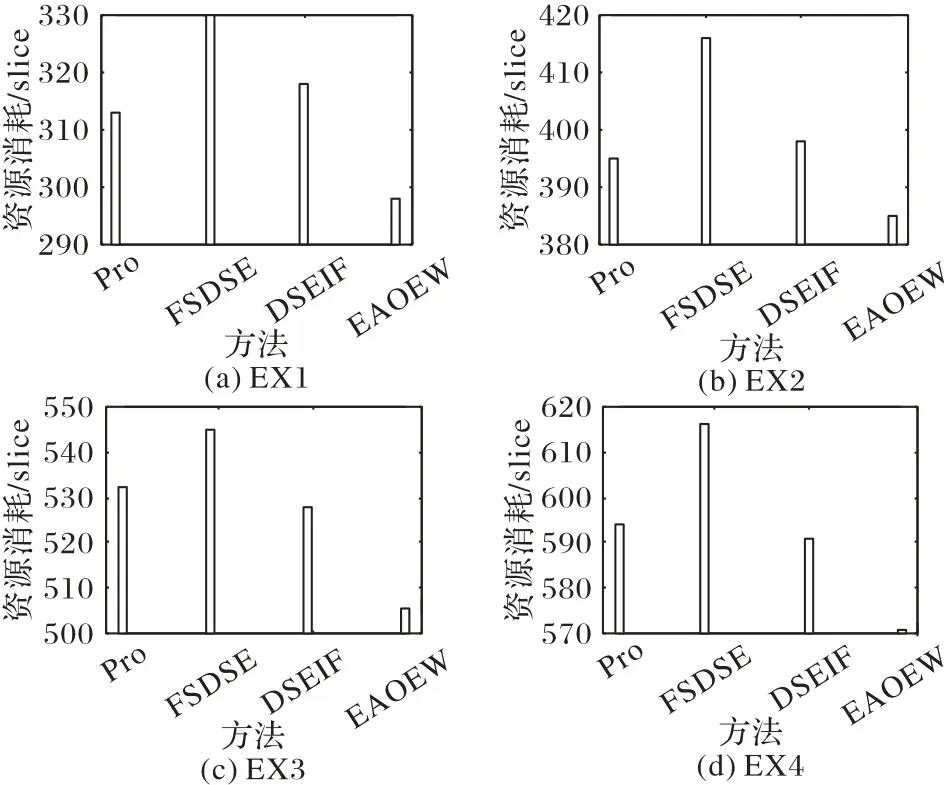
图5 四种方法的资源消耗对比Fig.5 Resource consumption comparison of four methods

3.4 设计空间探索时间对比分析

因为本文方法与DSEIF 方法在计算精度、计算时间与资源消耗等方面性能相当，为进一步对比两种设计空间探索方法，用设计空间探索的时间对二者进行对比分析。设计空间探索时间是指在PC平台上，利用浮点表达式设计空间探索方法对等价的浮点表达式及其邻域进行探索，直到得到最优表达式所需要的时间，可体现设计空间探索方法的效率。

图6 为两种设计空间探索方法对不同表达式进行探索的时间对比。本文提出方法的设计空间探索时间要优于DSEIF方法，尤其当浮点表达式结构复杂时，其时间优势越明显，例如对表达式x(x+2z)+y(y+2x)+z(z+2y)，本文提出方法的空间探索时间比DSEIF 方法缩短了89 s。主要原因是：DSEIF 方法需要对整个设计空间进行探索，探索效率低；而本文方法在保证对非支配表达式的邻域进行探索的前提下，对可支配列表中的表达式进行选择性的探索，在保证覆盖整个搜索空间的同时，有效提高了设计空间探索的效率。

图6 设计空间探索时间对比Fig.6 Design space exploration time comparison

4 结语

本文对浮点表达式设计空间探索的问题进行研究，针对已有的方法空间探索效率低下和计算性能差等问题，提出一种基于启发搜索的浮点表达式设计空间探索方法，并与现有的具有代表性的浮点表达式设计空间探索方法对典型的浮点表达式进行实验对比，实验结果表明本文提出的浮点表达式设计空间探索方法，在有效提高空间探索效率的前提下，得到的等价表达式具有更高的计算精度、更低的计算时间和资源消耗。