Analysis of the Dynamic System of Wave Glider with a Towed Body
2020-09-28ZHANGJiakunCHANGZongyuLUGuiqiaoZHENGZhongqiangandZHANGZhonglin
ZHANG Jiakun, CHANG Zongyu, LU Guiqiao, ZHENG Zhongqiang, and ZHANG Zhonglin
Analysis of the Dynamic System of Wave Glider with a Towed Body
ZHANG Jiakun1), 2), CHANG Zongyu1), 2), LU Guiqiao1), 2), ZHENG Zhongqiang1), and ZHANG Zhonglin3), *
1) College of Engineering, Ocean University of China, Qingdao 266100, China 2) Key Laboratory of Ocean Engineering of Shandong Province, Qingdao 266100, China 3) College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China
Mobile observation platforms are widely used in oceanographic and marine resource exploration and other applications. Wave Glider is a mobile platform that can transform wave energy into locomotion power and overcome the bottleneck of low energy supply. Wave Glider has recently been applied to tow underwater sensors fulfilling observation tasks. In this paper, the dynamic system of Wave Glider with a towed body is studied by applying multibody mechanics, and the relevant motion conditions of the system are investigated. Dynamic models of Wave Glider with a towed body and tether are first developed individually and then integrated into a whole model. The numerical method is used to obtain the dynamic responses and assess performance of the towed body pulled by the submerged glider of Wave Glider. The effects of sea state, mass of the towed body, and length of the towed cable are investigated on the basis of simulation results. This work can be used for the design and analysis of Wave Glider-towed body systems.
Wave Glider; towed system; motion response; dynamic analysis
1 Introduction
Mobile maritime platforms are important tools in marineenvironmental observation systems because they can per- form surveillance tasks over a wide range of sea domains. However, inadequate energy supply limits the application of these platforms for long-term observations. Wave Glider is a two-body unmanned surface vehicle consisting of a float connected to a submerged glidera flexible um- bilical; it can directly transmit wave motion to the pro- pulsion, thus solving the problem of low energy supply during long observation periods.
Researchon Wave Glider has been carried out in differentcountries, and dynamic analyses of Wave Glider have been conducted by using Kane’s equation (Zhang, 2017; Zhou, 2017), the Newton-Eulerian method (Kraus, 2012), and the Lagrangian method (Caiti, 2011). Liu(2014), for instance, analyzed the influence of fin interval distance on the propulsive performance of the submerged glider. Yu(2016) established a dynamic model of Wave Glider by simplifying the relevant motion equations through omission of high-order terms with small values. The relationships among the heave motion ofWave Glider, the stiffness ofelastic components, and the forward velocity can be obtained by using these simpli- fied equations. Andersen(2017) analyzed the effects of Strouhal number on heave or pitch motion and discussedthem in relation to changes in wake structures.Qi(2019) analyzed the effects of the pitch amplitude and frequency of the fins on the motion of Wave Glider and designed a non-sinusoidal pitch profile for fins. The mo- tion control of Wave Glider mainly uses PID controls (Shi, 2014).
Towed systems feature sensors or a sensor array, such as sonar, hydrophone, and so on, pulled by a surface ship or underwater vehicle; it is a powerful means to accom- plish studies on oceanographic research, marine geologi- cal surveys, and naval defense, among others. The motion of the towed system is strongly nonlinear and time-vary- ing; thus, many researchers have studied these systems from different aspects. Methods to analyze the towed sys- tem mainly include experiments, theoretical analyses, and numerical simulations. Rispin (1980) carried out a series of offshore experiments involving a complete towed sys- tem to test the performance of the towed cable. Wu and Chwang(2000)establishedafullythree-dimensionalmodel of a two-part underwater towed system and analyzed the motion responses of the depressor and towed body. Wang(2007) established a model of cable systems with variable lengths based on the finite segment method; here, the authors described the cable by changing the length of the segment near the towing point and increasing or de- creasing the number of discrete segments of the cable. Matulea(2008)introducedanewmathematicalmodel and matching numerical method based on finite differ- ences to predict the static configuration of towed com- pound cables. Sun(2011) analyzed the nonlinear dynamics of a cable-towed body system using a new nodal position finite element method to model and evaluate the cable. This method directly calculates the position of the cable, rather than its displacement,the existing finite element method. Yang. (2013) used the lumped pa- rameter model to establish three-dimensional motion equa- tions considering the bending and torsional effects of a marine towed cable system under large elastic deforma- tion conditions. Park and Kim (2015) built a 6-DOF dy- namic model of the towed system and analyzed the re- sponses of this system during straight running and U-turn- ing motion.
Because Wave Glider presents the advantages of long endurance, good communication, and low noise, this tech- nology is well suited for towed systems (Manley and Hine, 2016). Several attempts have been made to use Wave Glider as an underwater towed system for environmental observations (Wiggins., 2010; Guerra., 2016; Moh., 2017). The structure of a Wave Glider-towed system is shown in Fig.1. Wave Glider produces heave motion and an oscillating forward speed, which may af- fect the motion of the towed body. A towed body or sen- sor with stable motion is essential for collecting data. Thus, analyzing the effect of heave motion of the submerged glider on the towed body is important. In this study, a dynamic model of the Wave Glider-towed body system is established by considering the hydrodynamic forces act- ing on different system components. Then, the dynamic responses of the Wave Glider-towed system are analyzed on the basis of this model, and the horizontal velocity and vertical displacement of the towed body are studied under different structural parameters and sea states.
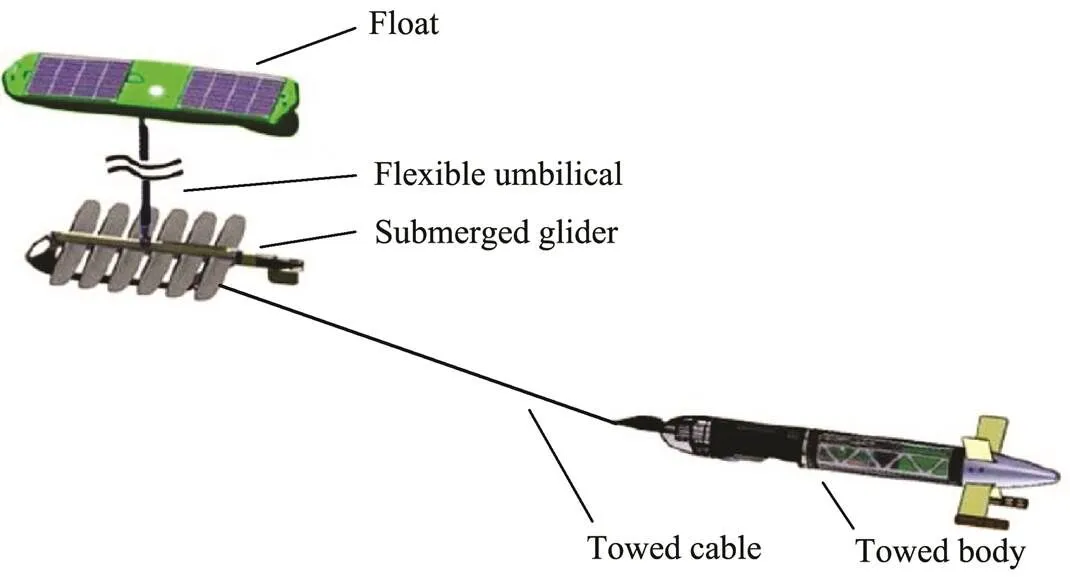
Fig.1 Illustration of the Wave Glider-towed system.
2 Wave Glider-Towed System Model
A model of the Wave Glider-towed system is illustrated in Fig.2; the dynamic model is presented in theplane, and the global frame is presented in this figure.
Some assumptions are proposed as follows to simplify the calculations:
1) The effect of current is ignored and the Wave Glider moves forward through the seawater without a current.
2) The umbilical is kept tensioned, and the centroid of the float coincides with the lifting point of the umbilical.
3) The hydrodynamic force on the fins is derived from the pressure distribution generated by the seawater on the fin surface, the vortex and wake flow caused by the fin disturbance are neglected, and the force on the fins is simplified to the force on the centroid of the fin.
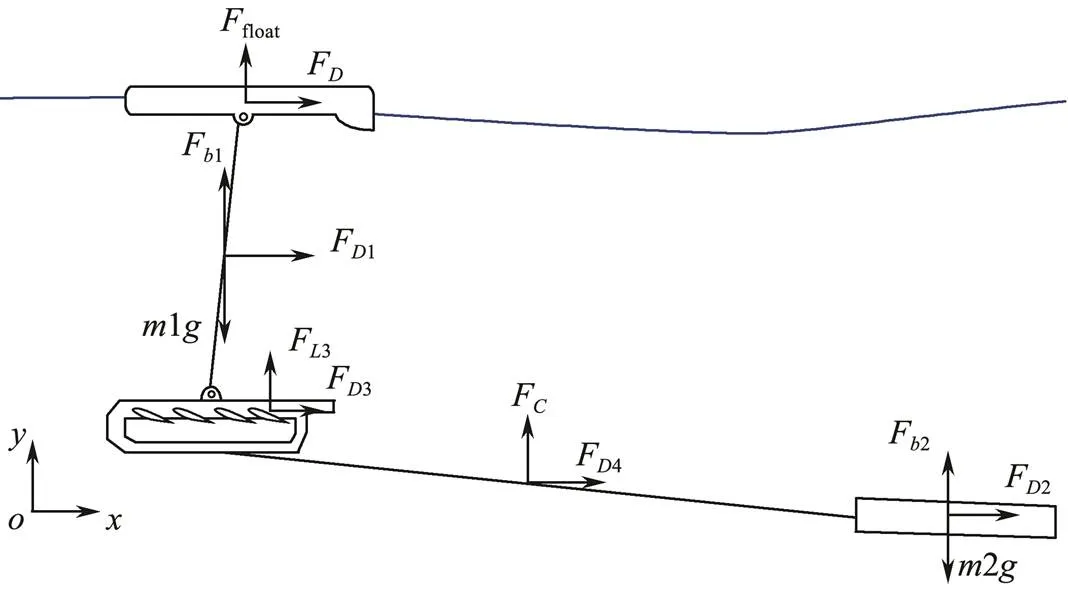
Fig.2 Model of the Wave Glider-towed system.
The force in the vertical direction of the float includes buoyancy and gravity and is defined as follows:

whereis the mass of the float body,is the density of seawater,is the cross sectional area of the float,is the draft of the float at some initial time, and1is the varia- tion of this draft.
The hydrodynamic force of the float is given on the ba- sis of the Morison equation:

whereCis the drag coefficient of the float,is the pro- jected area of the immersed portion perpendicular to the flow direction, anduis the horizontal velocity of the float.
The force of the umbilical is given as follows:
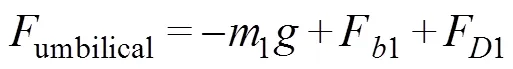
where1is the mass of the umbilical,F1is the buoyancy of the umbilical, andF1is the hydrodynamic force of the umbilical.F1can be solved by the Morison equation.
The force of the towed body is given as follows:
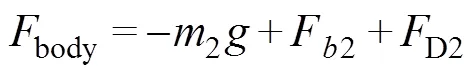
where2is the mass of the towed body,F2is the buoy- ancy of the towed body, andF2is the hydrodynamic force of the towed body, which can also be solved by the Morison equation.
The hydrodynamic force of each fin can be expressed as follows:

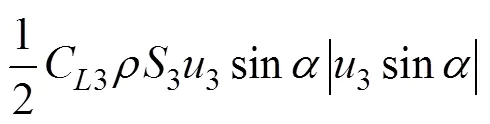
whereF3is the drag force of the fin,F3is the lift force of the fin, C3is the drag coefficient of the fin,C3is the lift coefficient of the fin,3is the projected area of the fin perpendicular to the flow direction,3is the horizontal velocity of the fin, andis the attack angle of the fin.
A cable is used to connect the floating body, submerged glider, and towed body. The cable model is discretized as segments connected by springs and dampers (Zhou, 2004), as shown in Fig.3. The parameters of the spring and damper depend on the properties of the cable or tether and the length of the segment. According to the model of the finite segment method, stiffness can be represented as a matrix of stiffness, as shown in Eq. (7).
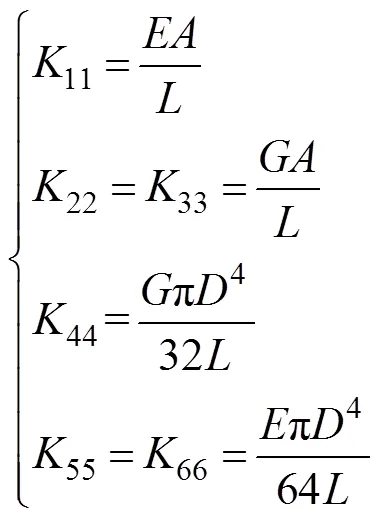
where11is the tensile stiffness coefficient,22and33are the shear stiffness coefficients,44is the torsional stiffness coefficient,55and66are the bending stiffness coefficients,is the elastic modulus,is the shear modulus,is the cross-sectional area of the towed cable,is the diameter of the towed cable, andis the length of the cable segment.
The hydrodynamic forceF4and force in the vertical directionFof each cable segment are given as follows:

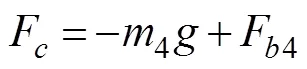
whereC4is the drag coefficient of the cable segment,4is the projected area of the cable element perpendicular to the flow direction,4is the horizontal velocity of the ca- ble segment,4is the mass of the cable element, andF4is the buoyancy of the cable segment.

Fig.3 Model of the towed cable.
3 Simulation of the Motion of the Wave Glider-Towed System
3.1 Parameters
The relevant parameters of the Wave Glider-towed sys- tem are shown in Table 1.
The wave parameters of different sea states can be de- termined as shown in Table 2 according to the wave pe- riod formula proposed by Bretschneider (1958).
The towed cable with a total length of 6m is discretized as 60 unified segments connected by a bushing force. Each segment has a length of 100mm and a radius of 10mm (Guerra, 2016). The towed body is simplified as a cylindrical body with a length of 600mm and radius of 50mm according to the size of the Mini VR2C Cabled Receiver. The mass of the towed body is 0.7kg.

Table 1 Parameters of the Wave Glider-towed system
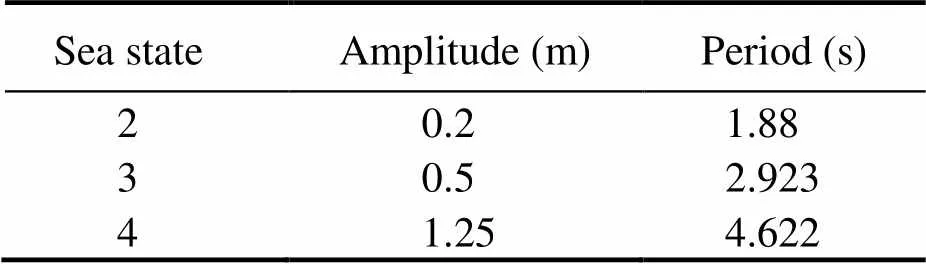
Table 2 Simulated sea state parameters
3.2 Dynamic Responses of the Wave Glider-Towed System
The motion responses of the Wave Glider-towed sys- tem under sea state 2 are calculated. The trajectories of the mass point of the floating body, the submerged glider, and the towed body are shown in Fig.4. The heave mo- tions of the three bodies are significant. In addition, the towed body shows obvious pitch motion and an oscilla- tory forward velocity due to the influence of the sub- merged glider. This may hinder towed bodies from col- lecting data.
The dynamic responses of the Wave Glider-towed sys- tem in the time domain under sea state 2 are shown in Fig.5. The heave motion presented in Fig.5(a) has an am- plitude of approximately 0.165m, which is slight smaller than that of the submerged glider. The forward velocities of the submerged glider and towed body are shown in Fig.5(b) and approximately equal. The towed body shows obvious heave motion and an unstable forward velocity, which can affect the measurement precision of towed sen- sors. Hence, analyzing the dynamic behaviors and effects of factors, such as mass and sea state, on the operating stability of the Wave Glider-towed system is necessary.

Fig.4 Motion responses of the Wave Glider-towed system.

Fig.5 Motion responses of the Wave Glider-towed system.
3.3 Effect of Environmental and Design Factors on the Performance of the Wave Glider-Towed System
3.3.1 Effect of length of the towed cable
The effects of several factors, such as environmental and design parameters, on the responses of the Wave Glider-towed system are investigated in this section. The motion responses of a towed body connected by cables measur- ing 4, 6, and 10m are analyzed under sea state 3, and the vertical displacement and horizontal forward velocity of the centroid of this body are obtained by simulation, as shown in Figs.6(a) and 6(b), respectively.
As the length of the towed cable increases, the ampli- tude of the heave motion slightly decreases. As shown in Fig.6(a), the vertical displacement of the model with the 10m cable is 16.88% less than that of the model with the 4m cable. In Fig.6(b), the average and fluctuation values of the forward velocity of the towed body decrease with increasing length of the cable.

Fig.6 Effect of length of towed cable on the motion of the towed body.
3.3.2 Effect of mass of the towed body
The effect of the mass of the towed body on the per- formance of the towed system is studied. The buoyancy of a towed body is neutral. The motion responses of the Wave Glider-towed system when the masses of the towed body are 0.7, 0.77, 0.84, and 0.91kg were analyzed under sea state 3, and the results of vertical displacement and forward velocity are shown in Figs.7(a) and 7(b), respec- tively.
As the mass of the towed body increases, the amplitude of the heave motion of the towed body increases and the towed body adopts a lower position during the operation of the Wave Glider-towed system. Increasing the mass of the towed body exerts only a slight influence on the fluc- tuation of the horizontal velocity. Thus, the towed body should haveneutral or slightly negative buoyancy to im- prove the stability of the Wave Glider-towed system.
3.3.3 Effect of wave parameters
The motion responses of the Wave Glider-towed sys- tem were analyzed under sea states 2, 3, and 4, and the vertical displacement and horizontal velocity of the cen- troid of the towed body were obtained by simulation, as shown in Fig.8.
Fig.8 reveals that the wave parameters have an obvious influence on the performance of the Wave Glider-towed system. The average velocity of the system in sea state 2 is approximately 0.94ms−1, the average velocity in sea state 3 is approximately 1.18ms−1, and the average veloc- ity in sea state 4 is approximately 1.38ms−1. In addition, the more severe the wave motion, the greater the average velocity and the higher the oscillation of heave motion and forward velocity of the towed body.

Fig.7 Effect of wave parameters on the motion performance of the towed body.

Fig.8 Effect of wave parameters on the motion performance of the towed body.
4 Conclusions
In this paper, the dynamic system of Wave Glider with a towed body is analyzed, and the motion characteristics of the towed body in this system are studied. Some conclusions are obtained as follows:
1) A dynamic model of the Wave Glider-towed system is established, and the responses of a body towed by Wave Glider could be obtained by the numerical integration method.
2) The towed body in the Wave Glider-towed system shows obvious heaving motion and a fluctuating forward velocity due to the influence of the submerged glider’s motion. The motion of the towed body is similar to that of the submerged glider.
3) Some factors, such as length of the cable, mass of the towed body, and sea state, exert significant effects on the performance of the towed body. The results can be used to design and analyze whole systems including Wave Gli- der and towed bodies.
Acknowledgement
The authors are grateful for the support of the National Natural Science Foundation of China (No. 51875540).
Andersen, A., Bohr, T., Schnipper, T., and Walther, J. H., 2017. Wake structure and thrust generation of a flapping foil in two-dimensional flow., 812 (R4): 1-12, DOI: 10.1017/jfm.2016.808.
Bretschneider, C. L., 1958. Selection of design wave for off- shore structures., 84 (2): 1-37.
Caiti, A., Calabró, V., Grammatico, S., Munafó, A., and Stifani, M., 2011. Lagrangian modeling of the underwater Wave Glider.. Santander, Spain, 1-6.
Guerra, L. A. A., Center, P. R. D., Soares-Filho, W., Barreira, L. M., Pai, S., and Schlumberger, L. R. O. G., 2016. Brazil off- shore underwater acoustic noise monitoring using autono- mous marine vehicle.
Kraus, N. D., 2012. Wave Glider dynamic modeling, parameter identification and simulation. PhD thesis. University of Ha- waii at Manoa.
Liu, P., Su, Y. M., Liu, H. X., and Liao, Y. L., 2014. Propulsive performance analysis of tandem asynchronous flapping foil., 48 (4): 457-463, DOI: 10.16183/j.cnki.jsjtu.2014.04.003 (in Chinese).
Manley, J. E., and Hine, G., 2016. Unmanned surface vessels (USVs) as tow platforms: Wave Glider experience and results.. Monterey, USA, 1-5.
Matulea, I. C., Năstase, A., Tălmaciu, N., Slămnoiu, G., and Gon- çalves-Coelho, A. M., 2008. On the equilibrium configuration of mooring and towing cables., 30 (2): 81-91, DOI: 10.1016/j.apor.2008.06.002.
Moh, T., Jang, N., Jang, S., and Cho, J. H., 2017. Application of a winch-type towed acoustic sensor to a wave-powered unmanned surface vehicle., 67 (1): 125-128, DOI: 10.14429/dsj.67.10577.
Park, J., and Kim, N., 2015. Dynamics modeling of a semi-submersible autonomous underwater vehicle with a towfish towed by a cable., 7 (2): 409-425, DOI: 10.1515/ijnaoe-2015-0029.
Qi, Z., Zhai, J., Li, G., and Peng, J., 2019. Effects of non-sinusoidal pitching motion on the propulsion performance of an oscillating foil., 14 (7): e0218832, DOI: 10.1371/journal.pone.0218832.
Rispin, P. P., Webster, B. L., Stasiewicz, J., and Diggs, J. S., 1980. Faired tow cable with stubs for strum reduction. U.S. Patent and Trademark Office, Washington, DC, Patent No. 4190012.
Shi, J., Gong, W., Qi, Z. F., Jia, L. J., Zhang, S., and Qin, Y. F., 2014. Research of Wave Glider navigation control strategy based on multi-sensor., 33 (6): 23-26, DOI: 10.3969/j.issn.1000-9787.2014.06.007 (in Chinese with English abstract).
Sun, F. J., Zhu, Z. H., and Larosa, M., 2011. Dynamic modeling of cable towed body using nodal position finite element me- thod., 38 (4): 529-540, DOI: 10.1016/j.oceaneng.2010.11.016.
Wang, S. X., Wang, Y. H., and Li, X. P., 2007. Dynamic analysis of Towed and variable length cable systems., 21 (2): 331-341, DOI: 10.3321/j.issn:0890-5487.2007.02.013.
Wiggins, S., Manley, J., Brager, E., and Woolhiser, B., 2010. Monitoring marine mammal acoustics using Wave Glider.. Seattle, 1-4.
Wu, J. M., and Chwang, A. T., 2000. A hydrodynamic model of a two-part underwater towed system., 27 (5): 455-472, DOI: 10.1016/S0029-8018(99)00006-2.
Yang, B. K., Zhu, K. Q., Zhu, Y. J., and Qin, D. W., 2013. Dynamic response of towed line array., 25 (4): 616-619, DOI: 10.1016/S1001-6058(11)60403-5.
Yu, Z. J., Zheng, Z. Q., Yang, X. G., and Chang, Z. Y., 2016. Dynamic analysis of propulsion mechanism directly driven by wave energy for marine mobile buoy., 29 (4): 710-715, DOI: 10.3901/CJME.2016.0317.032.
Zhang, Y., Bo, Y. Q., and Liu, H. F., 2017. Analysis on hydro- dynamic performance of the Wave Glider., 39 (3): 123-126, DOI: 10.3969/j.issn.1009-0134.2017.03.032 (in Chinese).
Zhou, C. L., Wang, B. X., Zhou, H. X., Li, J. L., and Xiong, R., 2017. Dynamic modeling of a Wave Glider., 18 (9): 1295-1304, DOI: 10.1631/fitee.1700294.
Zhou, Y., Yi, J. J., and Zheng, J. R., 2004. Modeling flexible rigging in ADAMS software., 2004 (5): 38-39, DOI: 10.16731/j.cnki.1671-3133.2004.05.015 (in Chinese with English abstract).
. E-mail: zhangzhonglin@hrbeu.edu.cn
September 23, 2019;
December 9, 2019;
December 12, 2019
(Edited by Xie Jun)
杂志排行
Journal of Ocean University of China的其它文章
- Diffusion Characteristics of Swells in the North Indian Ocean
- Provenance and Tectonic Implications of Paleozoic Strata in the South Yellow Sea Basin, China–Revealed from the Borehole CSDP-2
- Ecological Risk of Heavy Metals in Sediment Around Techeng Island Special Marine Reserves in Zhanjiang Bay
- Geochemical and Grain-Sized Implications for Provenance Variations of the Central Yellow Sea Muddy Area Since the Middle Holocene
- Grain-Size Distribution of Surface Sediments in the Bohai Sea and the Northern Yellow Sea: Sediment Supply and Hydrodynamics
- Path Planning and Navigation of Oceanic Autonomous Sailboats and Vessels: A Survey
