基于逐步回归分析法的整车热平衡试验数据研究

王继磊，徐艳杰，赵伟，刘刚，朱江苏

1.内燃机可靠性国家重点实验室，山东 潍坊 261061；2.潍柴动力股份有限公司 发动机研究院，山东 潍坊 261061

0 引言

发动机匹配整车后，需通过整车热平衡试验来检验整车所适用的环境温度是否符合企业要求［1-4］。文献［5］也对此有明确的道路试验方法要求。由于道路试验具有难度大、时间长、环境依赖强等缺点，目前多用转毂热平衡试验代替道路试验。

为了优化冷却系统部件，整车上需安装许多传感器，但如果要定量分析各冷却部件如水泵、散热器、中冷器、风扇等在整车上的性能，还需输入和测试很多参数［6-9］，目前通过道路试验和转毂热平衡试验几乎都无法做到。

如果利用易于测量的参数，构建其与许用环境温度之间的关系，分析已有测试参数对最终试验结果的影响，则可为查找定位冷却系统问题及其优化设计提供方向。

1 热平衡测试参数

整车热平衡按照迎面风路、发动机进气路和冷却介质流动路线布置相应传感器，测试各自路径中介质的温度变化，表1为转毂热平衡试验的测试项目及传感器安装位置［10-14］。

目前转毂热平衡试验能得出许用环境温度，给出整车的有关温度参数是否符合要求，也可根据测试的温度数据判断热回流、进排气阻力和评估需要改进的部件，但没有量化的指标表明哪些部件存在问题，明确哪些指标已经超限。

本文选取环境温度、中冷器前后空气温升、增压气体温度与环境温度的平均温差、中冷器后温度与环境温度差、散热器进出水温差、散热器前后空气温升等10个参数作为自变量，利用回归分析法建立许用环境温度与转毂热平衡各试验参数间的等效关系式，量化分析各参数对环境温度的贡献量。

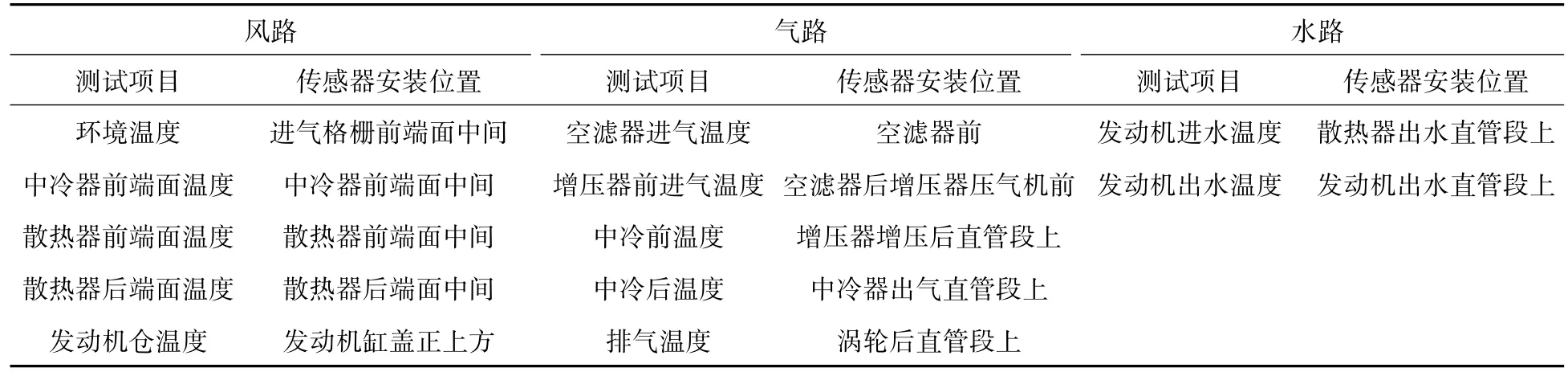
表1 转毂热平衡试验的测试项目及传感器安装位置

2 回归分析

回归分析是确定两种及两种以上变量间相互依赖的定量关系最常用的数据分析方法之一［15］，按照涉及变量的多少，可分为一元回归分析和多元回归分析。文章选取的变量较多，属于多元回归分析。多元回归分析常常从可能影响因变量的许多因素中挑选某些因素作为自变量，从而建立最优回归方程。其基本思想为：将自变量逐个引入，每引入一个自变量后，对已引入的变量进行逐个检验，当原引入的变量由于后面变量的引入而变得不再显著时，剔除原引入变量（变量剔除时显著性水平一般为0.01），反复进行此过程，直到既无显著的自变量引入回归方程，也无不显著的自变量从回归方程中剔除为止。

2.1 自变量及试验样本数据确定

与许用环境温度直接相关的部件为水泵、散热器和风扇［16-19］，但有些部件的性能评价参数无法测量［20-22］，统计整理19辆轻中型载货汽车的转毂热平衡试验数据，结合经验，选取大扭矩点平衡的数据作为分析样本数据，选取参数x1～x10为自变量，即：环境温度x1、中冷器前后空气温升（冷却空气经过中冷器部件的空气温升）x2、中冷器前空气温升（中冷器前温度与环境温度的差值）x3、中冷器进出气温差（增压器增压后气体温度与经过中冷器冷却后气体温度的差值）x4、增压后气体温度与环境温度的平均温差x5、中冷器后温度与环境温度的差值x6、散热器进出水温差x7、散热器前空气温升x8、发动机出水与冷却空气平均温差x9、散热器前后空气温升x10，共19组，整车最终许用环境温度为因变量，其中许用环境温度统一按最高出水温度103℃计算。

2.2 回归分析

应用MATLAB进行逐步回归分析，计算结果如图1所示。逐步回归分析后，x1、x3、x7变量被剔除，得到许用环境温度T与主要影响参数之间的关系式：

T=91.202-0.465 814x2-0.198 659x4+0.765 864x5-1.190 270x6-0.280 296x8-0.280 424x9-0.734 962x10。 （1）

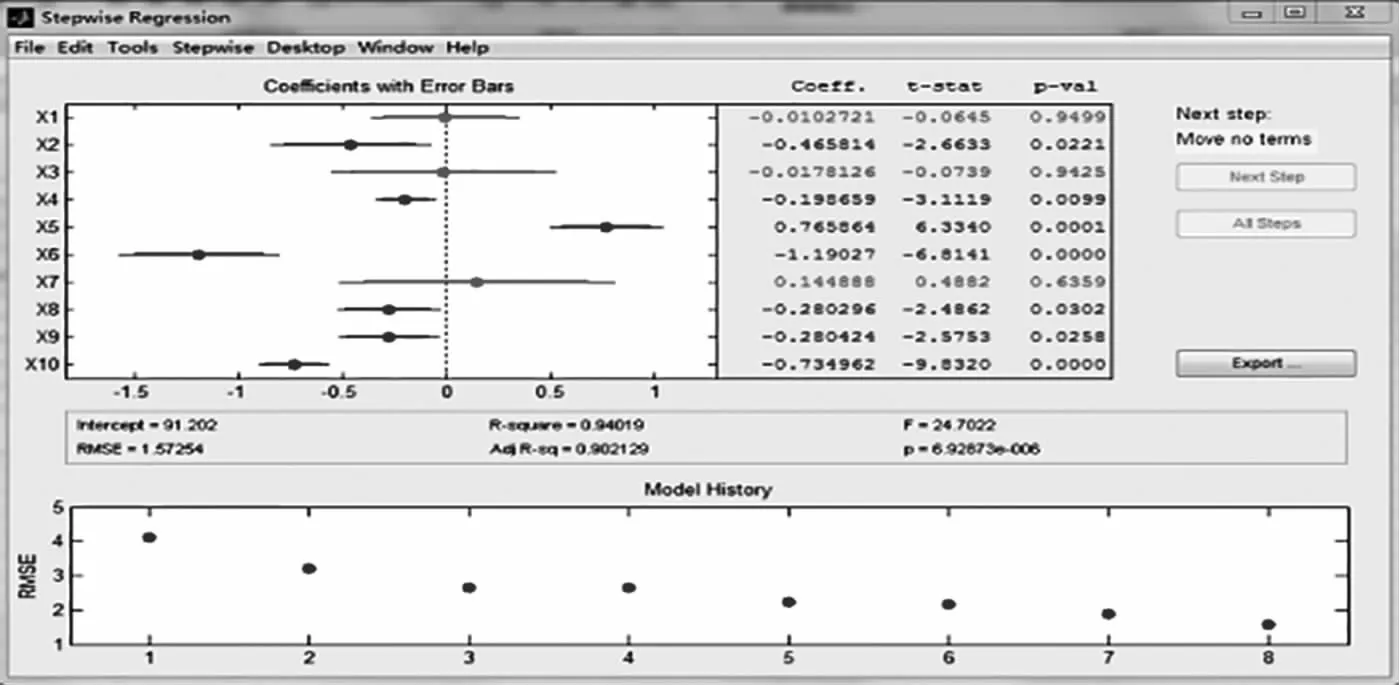
图1 逐步回归分析结果

式（1）中显著自变量参数对应的数据共19组，将19组数据分别代入式（1）计算出19辆整车的最终许用环境温度，得到计算许用环境温度与实际测试的许用环境温度的关系如图2所示。

由图2可知：运用多元回归分析的计算结果与实际测试结果吻合较好，拟合优度判定系数R2=0.940 2，说明该多元线性回归方程的拟合程度比较理想。

图2 回归计算与实际测试环境温度的关系

3 自变量的贡献量及推荐值

3.1 自变量的贡献量

由式（1）可知：通过x2、x4～x6、x8～x107个主要参数可以计算出许用环境温度。为了解正常情况下7个参数中哪些参数对最终结果影响显著，建立式（1）的等效关系式。令

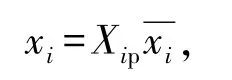
则式（1）的等效关系式为：

各自变量的贡献量为每个自变量系数的绝对值与系数绝对值总和之比。经式（2）计算每个自变量的贡献量如图3所示。

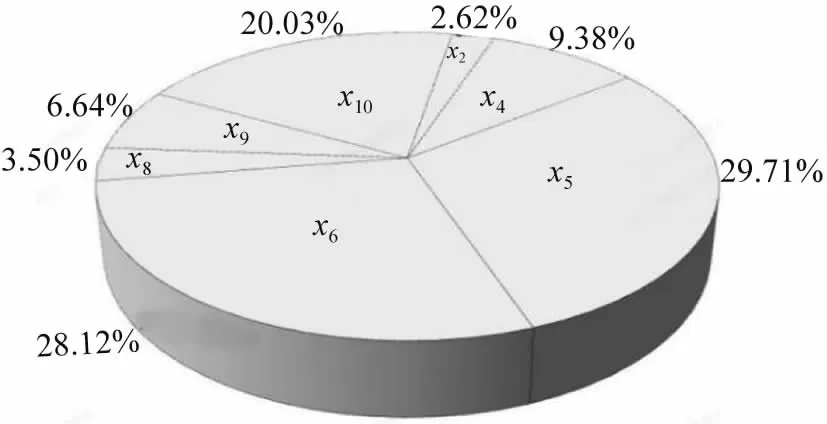
图3 不同参数对许用环境温度的贡献量

3.2 自变量的推荐值

依据式（1）中确定的7个主要参数，分析其与许用环境温度的关系，得出7个主要参数与整车转毂实测的许用环境温度关系的散点图，其中x2、x5、x8与T的散点图如图4～6所示。

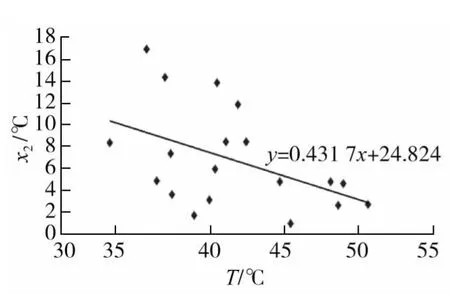
图4 x2与T的拟合关系

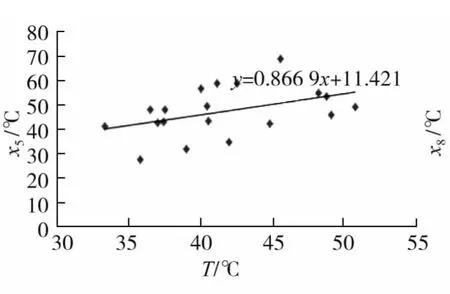
图5 x5与T的拟合关系

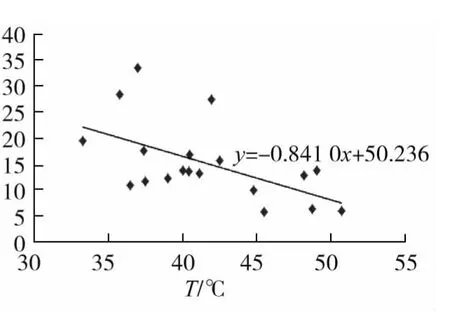
图6 x8与T的拟合关系

根据散点图可以拟合出许用环境温度与相应变量的线性关系。根据工程经验，许用环境温度达到40℃时，整车运行可以满足环境使用要求，所以分析许用环境温度达到40℃时自变量对应的数值，该数值定为推荐值，关键参数的推荐值见表2。将表2中的推荐值带入式（1），计算得到许用环境温度为40.06℃，结果与设计值一致。

热平衡试验结束后，可以统计参数x2、x4～x6、x8～x10的数值，并与表2中的推荐值对比，查找明显偏离推荐值的参数，从而找到与此相关的部件，对系统结构进行改进［23］。

表2 主要参数推荐值 ℃

4 结论

1）利用回归分析法建立许用环境温度与主要影响参数的关系式，量化了各参数的贡献量，并给出环境温度达到40℃时主要参数的推荐值，根据各主要参数的推荐值可以预测许用环境温度，以便为改善整车冷却系统的设计提供参考。

2）由于样本中自变量相对偏少，回归分析经验公式中依赖的参数较多，后续可以积累样本数量继续分析。