纯电动汽车纵向跟车动力学建模与分层控制

张亮修，陈鹏飞，张学义

1.上海保隆汽车科技股份有限公司，上海 201619；2.山东理工大学交通与车辆工程学院，山东 淄博 255000

0 引言

汽车纵向跟车系统能够实时有效地控制自车车速和自车与前车的安全车距，是汽车实现智能辅助驾驶的首要系统之一。纵向跟车系统涉及的方法可以归纳为最优控制［1-2］、滑模变结构控制［3-4］、模糊神经网络控制［5-6］、模型预测控制［7-8］、多模式切换控制［9-10］和深度学习［11-12］等。 目前对电动汽车纵向跟车控制系统的研究包括电动汽车自适应巡航系统建模［13-14］、混合动力车辆自适应巡航［15-16］、四轮轮毂电机车辆自适应巡航［17-18］、自适应巡航过程考虑再生制动［19-20］等。本文建立电动汽车纵向动力学模型，设计由决策层和实施层构成的分层控制架构，并基于Matlab/Simulink环境进行多工况仿真验证，以期提升电动汽车的纵向跟车性能。

1 电动汽车纵向动力学建模

电动汽车纵向动力学模型包括电动机、变速器、主减速器、车轮和整车纵向运动模型。

1）电动机模型

根据电动机台架实测的稳态特性曲线，并考虑其动态特性得到电动机模型

式中：Te为电动机动态输出扭矩，ne为电动机转速，im为控制电流，f（ne，im）表示电动机转速和控制电流的函数关系，τe为电动机时间常数，s为复变量，Ie为电动机转动部件有效转动惯量，ω·e为电动机角加速度，Tp为变速器输入扭矩。

2）变速器与主减速器模型

变速器和主减速器一起考虑，建立其传动方程

式中：It为变速器转动惯量，Twp为车轮驱动扭矩，ig为变速器速比，i0为主减速器速比，ω·t为变速器输出轴转动角加速度，ωwf为驱动车轮转动角速度。

3）车轮模型

车轮转动动力学方程为：

式中：Iw为车轮转动惯量分别为前、后轮转动角加速度，Ffx、Frx分别为前、后轮胎纵向力，Reff为车轮有效滚动半径，Tfwb、Trwb分别为前、后轮制动力矩，Tfx、Trx分别为前、后轮滚动阻力矩。

4）整车纵向运动模型

将车轮转动转化为整车纵向运动，忽略车轮滑动，整车纵向运动平衡方程为：

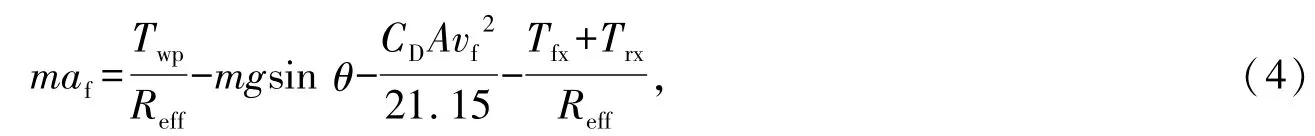
式中：m为整车质量；af为车辆纵向加速度；g为重力加速度；θ为道路坡度角；CD为空气阻力系数；A为迎风面积；vf为车辆纵向速度，vf=ωwfReff。

2 纵向跟车系统分层控制

如图1所示，纵向跟车系统采用决策层与实施层分层控制结构［21］。决策层控制器包括定速控制和定距控制，定速控制由比例积分微分（proportional integral differentiatial，PID）控制实现，定距控制综合距离、速度、实际加速度和期望加速度等多个指标，利用线性二次最优控制（linear quadratic regulator，LQR）优化得到期望的跟车加速度。实施层控制器基于加速度校正器和逆纵向动力学模型，确保车辆的实际控制加速度af，con实时准确地跟踪决策层输出的期望加速度af，des，图1中im，des、pw，des分别为期望的电机驱动电流和制动器制动压力，Δd为自车与前车间距误差，Δv为前车与自车的相对速度。

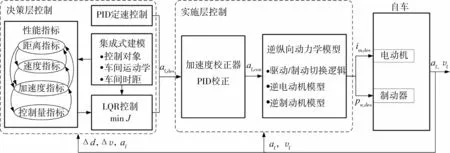
图1 自适应巡航系统控制策略架构

2.1 决策层控制器设计

决策层控制器根据自车前方是否有目标车辆，分为定速控制和定距控制。

1）自车前方未出现目标车辆

若自车前方未出现目标车辆，采用PID实现定速控制，速度误差

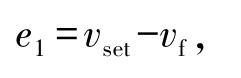
式中：vset为设定车速，vf为自车实际车速。

则期望加速度

式中KP1、KI1、KD1分别为PID控制的比例、积分和微分系数。

2）自车前方出现目标车辆

当自车前方出现目标车辆时，跟车系统进入定距控制模式，建立包含自车和车间关系的集成式纵向运动学模型［22］

跟车系统控制的最终目标是使自车与前车的实际车距趋近于期望车距，自车车速趋近于前车车速，以车间距误差和相对车速的2范数量化跟踪性能，即：

式中：J1为跟踪性能指标；q1、q2分别为相应的权系数，取q1=q2=1。

通过优化跟车过程中的加速度绝对值以提高跟车舒适性，以自车加速度的2范数量化舒适性能，即：

式中：J2为舒适性能指标；q3为相应的权系数，取q3=1。

为了限制加速度控制抖动，加入控制指标

式中：q4为控制输入权系数，取q4=12。

综合考虑Δd、Δv和af，并加入加速度控制量限值，联合式（7）～（9）设计纵向跟车优化性能指标

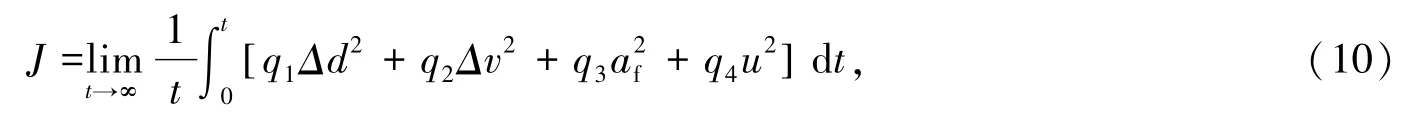
式中t为积分时间。

结合式（6）（10），得到性能指标

式中：Q=diag（[ q1q2q3]），R=q4。

纵向跟车车距控制转化为以式（11）为目标函数的优化控制问题，即期望的最优控制量

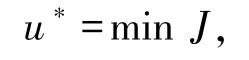
基于线性二次最优控制理论［23］，寻求最优反馈控制增益， 则期望最优控制加速度

2.2 实施层控制器设计

跟车过程需要不断进行驱动和制动的切换，从安全和节能角度，应避免同时驱动和制动。以车辆怠速带挡滑行试验数据为基础，拟合出车辆加速度与车速的关系作为驱动与制动的切换基准，同时为避免驱动力矩和制动力矩之间的频繁切换，设置切换基准的上、下偏置h1和h2，表1为驱动/制动切换逻辑。

1）驱动工况的电动机力矩

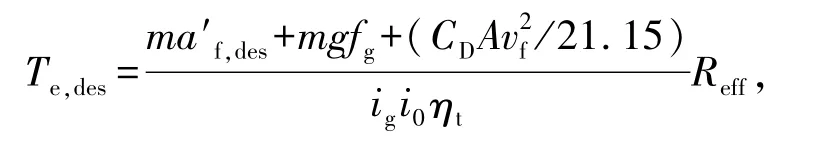
表1 驱动/制动切换逻辑

式中：fg为滚动阻力系数，ηt为传动系统效率。

已知Te，des，结合电动机转速，利用逆电动机模型（由电动机力矩和转速求得电流）求得期望的驱动电机控制电流

2）制动工况时的制动器制动力矩

制动工况时，应充分利用发动机阻力矩、空气阻力和滚动阻力，由此求得期望的制动器制动力矩

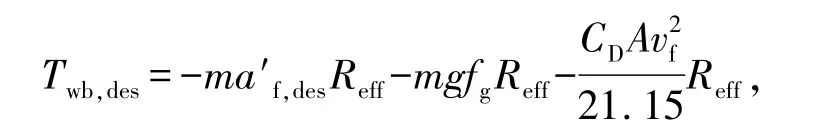
由逆制动器模型（由制动力矩求得制动压力）可得期望的制动压力

式中Kb为制动系统的制动增益系数。

3）控制加速度

为保证车辆实际加速度跟踪期望加速度的动态性和准确性，设计PID加速度校正器，校正误差

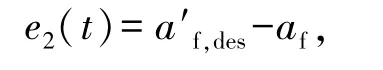
则实际控制加速度

式中KP2、KI2和KD2分别为PID控制的比例、积分和微分系数。

3 仿真验证

基于Matlab/Simulink搭建仿真模型，由式（5）（12）得到期望的最优控制加速度，通过表1切换逻辑和式（13）（14）将期望的加速度转换为驱动电机的电流和制动压力，并借助式（15）进行加速度校正，根据式（1）～（4）得到自车实际加速度、速度和位移，再结合给定的前车信息，得到相对车速和跟车车距。在前车先减速后加速、前车先制动后匀速2种工况下对控制算法进行验证，主要参数如表2所示。

表2 主要参数

3.1 前车先减速后加速工况

前车以20 m/s的初速度开始减速，约6 s时减速至12 m/s，约12 s时又加速到20 m/s，之后一直保持匀速行驶，仿真结果如图2所示。

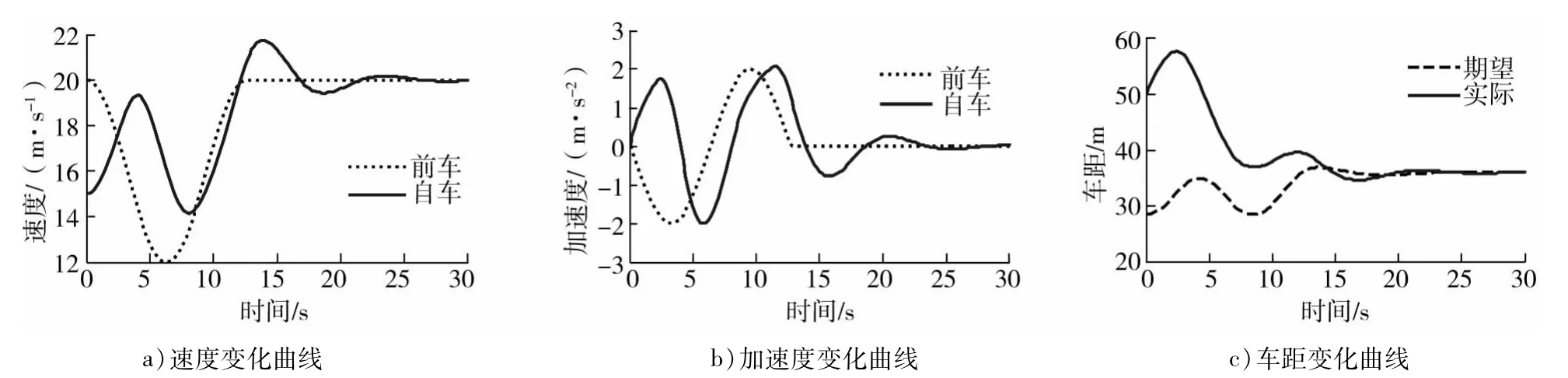
图2 前车先减速后加速工况速度、加速度、车距随时间的变化曲线

由图2a）知：因自车初速度小于前车初速度，故自车先加速，之后因前车减速，自车车速出现一定超调波动，最终随前车的匀速行驶而进入稳态跟车阶段，收敛速度较快。由图2b）、2c）知：实际车距趋于期望车距，并当前车加速度为0时，自车加速度也逐渐趋向于0。

3.2 前车先制动后匀速工况

前车以20 m/s的初速度开始减速，约15 s时减速至10 m/s，之后一直保持匀速行驶，仿真结果如图3所示。

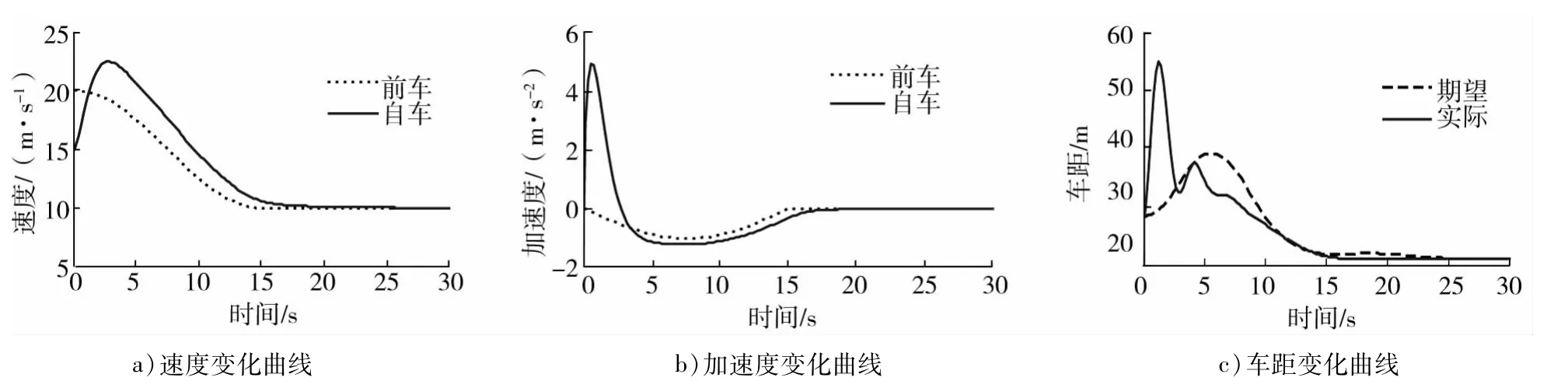
图3 前车先制动后匀速工况速度、加速度、车距随时间的变化曲线

由图3可以看出：控制算法能实现有效跟车功能，因自车初速度小于前车初速度，故自车车速先增加后减小，最终收敛于前车车速；自车加速度趋于前车加速度，实际车距趋于期望车距。

4 结论

1）建立包括电动机、变速器、主减速器、车轮与整车纵向运动模型的纵向动力学模型，为控制算法仿真验证提供载体。

2）从跟车系统的功能需求和控制目标出发，设计包括决策层和实施层的分层控制架构，其中决策层控制器基于线性二次最优控制理论优化得到期望的跟车加速度，实施层控制器基于驱动电机和制动器切换逻辑，设计PID加速度校正器，实现期望加速度跟踪。

3）Matlab/Simulink多工况仿真结果表明，所设计的控制算法能够控制自车保持良好的跟踪性和自适应性。