常规布局无人机自适应容错控制∗

（海军航空大学 烟台 264001）

1 引言

随着科技的发展，无人机不仅在多个层面内得到了广泛应用，还在自身性能上得到了质的提高，由此带来的无人机安全可靠性能方面存在的问题也越来越突出，设计无人机的容错控制方法，使其在一定故障状态下，依旧可以按照一定规律充分调节，以适应在错误与干扰状态下，持续稳定地飞行，进而提升飞行器控制系统的安全可靠性。

本文主要针对固定翼无人机进行控制仿真，在对于固定翼无人机的基本控制模型已有掌握的情况下，进行基于自适应方法的控制器设计，考虑固定翼无人机控制通道出现偏差，系统产生不确定性和故障的问题，通过假定偏差信号有界，但变化规律未知的基本条件，运用自适应方法，在线调节控制参数，使系统具有容错能力，通过设计好的控制律可以适当或完全补偿偏差带来的影响，最后通过Matlab/Simulink进行了仿真分析，验证自适应容错控制的有效性。

2 容错控制概述

随着科技的发展，无人机控制系统的日益复杂，发生事故的概率也在增加，通常出现故障事故，就有可能造成财产的巨大损失。例如，1998年，美国运载火箭——“大力神”、“雅典娜”、“德尔他”相继发生了5次发射事故，造成直接经济损失高达30亿美元，对美国的航天战略造成了沉重打击。

因此，提高飞行控制系统的可靠性与安全性至关重要，其中基于解析冗余的动态系统的故障诊断与容错控制（Fault Tolerant Control）则为提高复杂系统的可靠性开辟了一条新的途径。

容错控制是随着故障诊断技术而发展起来的。系统发生故障时，经过调节，闭环控制仍然是稳定的，并具有较为理想的响应特性，就称此闭环控制系统为容错控制系统。容错控制一般可以分成两大类，即被动容错控制和主动容错控制。

被动容错控制是由鲁棒控制衍生发展而来，其控制的要素是针对事先设定好的故障类型，要求该控制器不仅能够保证正常情况下的闭环系统稳定性，而且在预设好的故障情况下也能够确保闭环系统的动态品质达到稳定要求［1～2］。从被动容错控制的定义可以看出，其控制器具有固定的结构和参数，不需要进行实时的故障诊断，相对比较容易实现，这对飞行控制系统的设计来讲比较实用。但是，被动容错控制的最大缺点就是只对事先设定好的故障具有容错控制效果，对于设定范围之外的故障类型，往往就会出现失效情况，具有一定局限性。目前，被动容错控制大致可以分成可靠镇定、完整性设计和联立镇定［3］三种。

主动容错控制是在故障发生后迅速调整控制器的参数，亦可能重构控制器结构。多数主动容错控制含有故障诊断子系统，原因正是因为要对发生的故障进行主动处理这一事实。经过近30年的发展，主动容错控制技术已日趋成熟，所提出的方法详见有关文献。主动容错控制大致可以分为控制律重新调度，模型跟随重组控制，控制器重构设计三大类。

3 自适应容错算法设计

3.1 自适应容错控制

在容错控制中使用自适应方法主要有模型参考自适应容错控制和多模型自适应容错控制两种。

模型参考自适应容错控制不需要故障检测模块，在故障条件下，控制系统会自动调节控制律来保证被控对象的响应依然跟随参考模型的输出，以此实现容错控制的目的。可见这是采用被动的方式处理故障［4～7］。而多模型参考自适应容错控制在一定意义上与联立镇定相似，它依据故障的估测信息主动地对控制律进行调整以适应故障后的控制系统，从而降低系统对故障的敏感度，从而实现控制目的。

3.2 自适应容错控制器设计原理

下面将对固定翼布局无人机的自适应容错控制系统进行设计。

本文模拟的故障类型为无人机系统故障，通常情况下，系统故障是由无人机某些物理部件的损坏造成的，影响被控对象的结构或参数，导致飞行状态发生改变。

系统故障又分为状态故障与参数故障两种，对于系统状态故障，当系统状态发生改变时，其故障类型可表示为［8］

式中，∆x(t)表示故障函数，对于不同类型，∆x(t)函数表达形式亦不同。

对于系统参数故障，是指无人机工作时间延长后，气动参数发生偏移，直接影响设计控制律的建模参数。参数影响下的系统可以概略为参数矩阵的影响，具体系统方程为

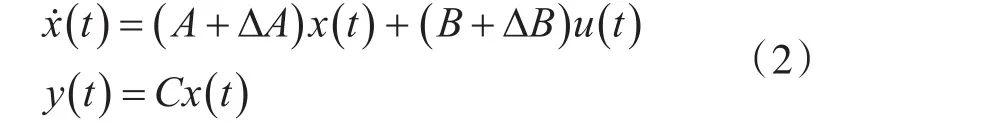
式中，∆A、∆B分别表示参数矩阵A和B的变化。

考虑如下只存在系统故障影响的状态方程：

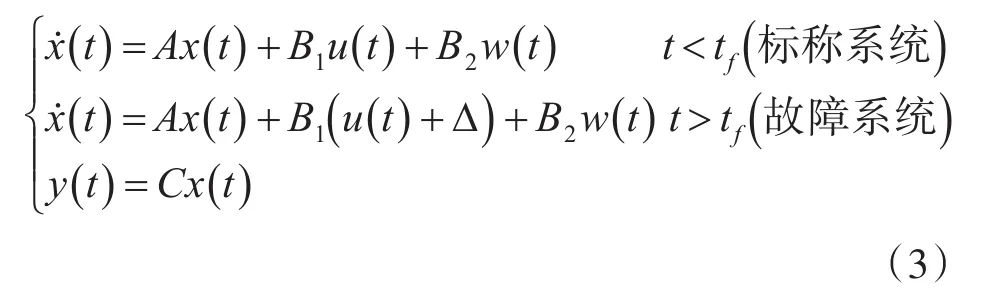
此时容错控制系统的结构控制器设计如下：

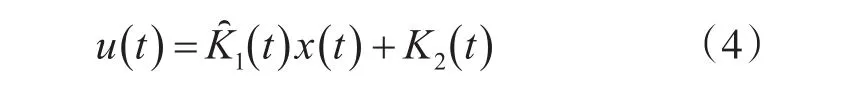
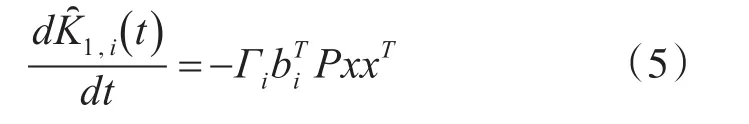
上式中，Γi是正常数，有边界，bi是B的第i列。控制器中的设计用来保证系统稳定性，控制的增益K2(t)则用来补偿系统故障带来的影响，下面列出控制增益的设计方法，该方法将保证系统在故障影响下的渐近稳定。

式（9）、（10）分别为闭环系统与误差系统，对于满足式（4）、（5）、（6）的自适应闭环系统，假定存在正定对称矩阵P，并选择式（6）作为控制增益方程，式（5）、（7）作为自适应律，则所得容错系统是渐进稳定的，该结论利用李雅普诺夫稳定原理即可证明。

通过以上设计过程，完成了对常规布局（固定翼）无人机自适应容错控制系统的设计，接下来，将在第4节对设计好的控制系统进行Matlab/Simulink仿真，分析控制性能。

4 基于Matlab/Simulink平台进行仿真分析

4.1 常规布局无人机数学与仿真模型

本节仿真将在无人机模型中进行容错控制器的运用，将上一节设计的自适应状态反馈控制器应用到该模型中，并给出故障状态下，容错控制的仿真效果图线，首先列举常规布局无人机数学模型公式［9～10］：

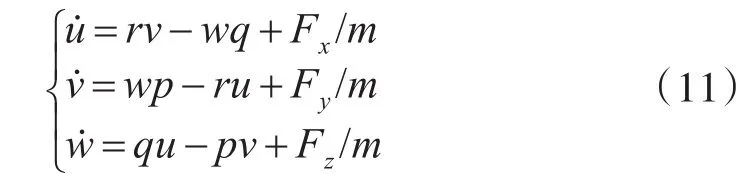
以上建立的无人机力学方程组，u，v，w分别表示机体坐标系在三个坐标轴上的速度分量。

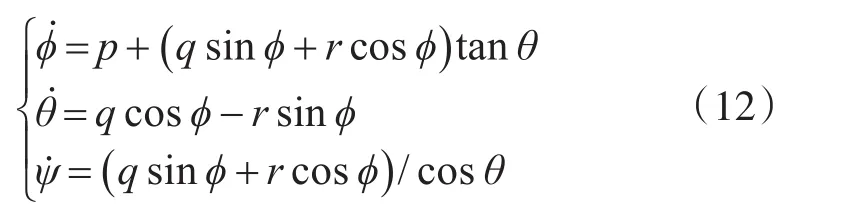
式（2）表示无人机运动学方程组，θ，ψ，ϕ分别表示无人机俯仰、偏航与滚转角。

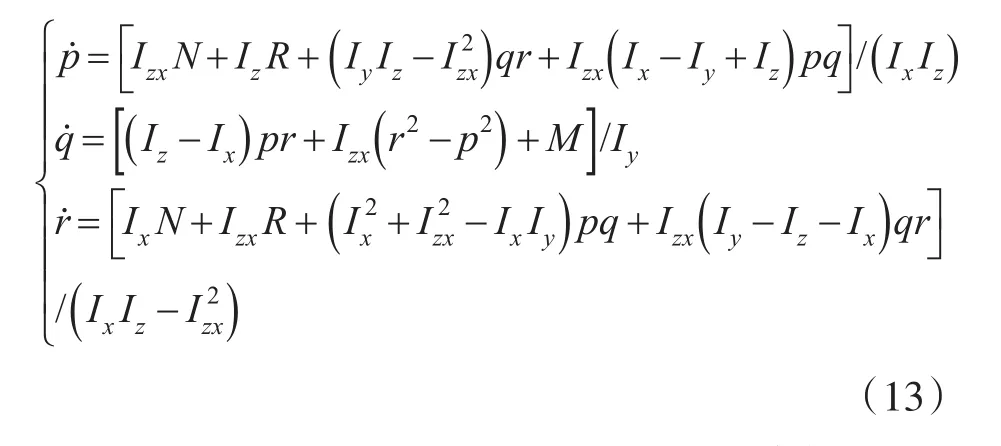
在力矩方程组中，p，q，r为三通道角速度，Ix，Iy，Iz为机体坐标系三轴转动惯量。

式（14）表示导航方程组，未知量表示常规布局无人机地面坐标系中在三轴上的位移分量。

为验证第3节自适应容错算法的有效性，根据以上无人机三通道六自由度的12个非线性数学模型方程，确定了无人机在空中运动模型的状态变量为与输入变量为之间的非线性函数关系。其中δe、δα、δr、δt分别表示升降舵偏角、副翼偏角、方向舵偏角、发动机油门开度。通过Matlab/Simulink使用S函数和Simulink进行控制系统模型搭建。

在无人机模型中，对其降阶动态飞行系统加入系统故障后的动态模型为

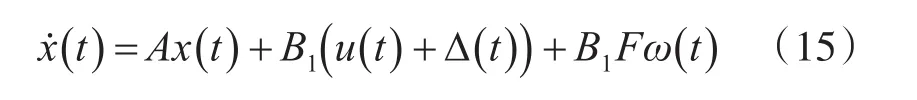
其中，设置初始仿真初始条件为，攻角α=30°，速度为0.2M，高度为16000m，配平后得到的系统矩阵为

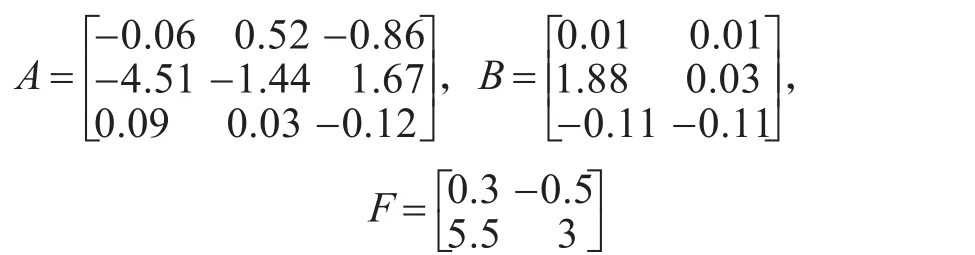
仿真时其他参数条件为

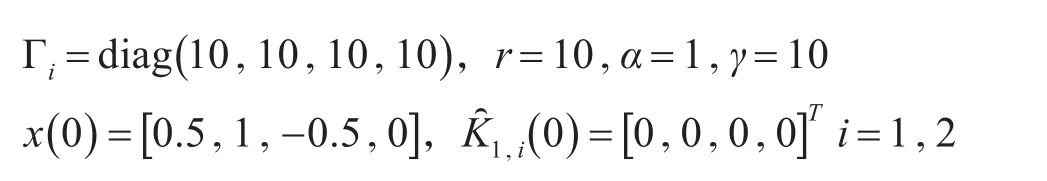
根据以上初始设置，建立如图1所示系统搭建模块的具体形式。

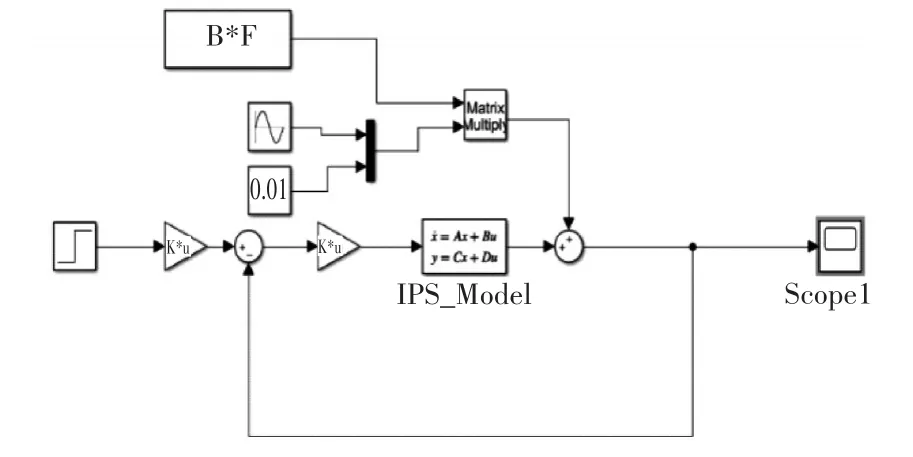
图1 控制系统Simulink搭建方式

当系统存在偏差，状态发生变化时，加入容错控制律的调节，得到无人机三通道状态响应，见图2～4。

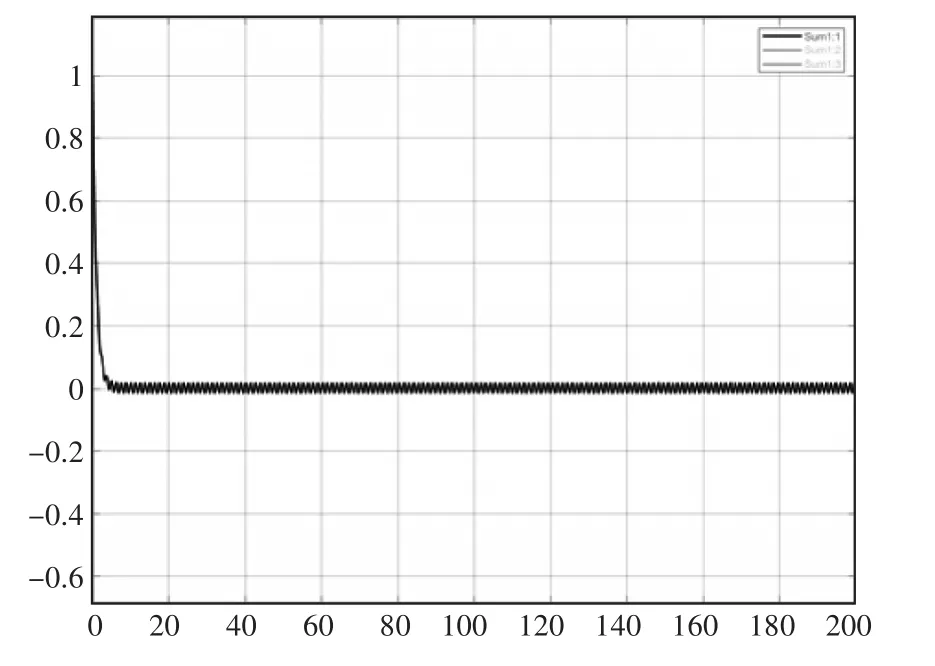
图2 俯仰角状态响应

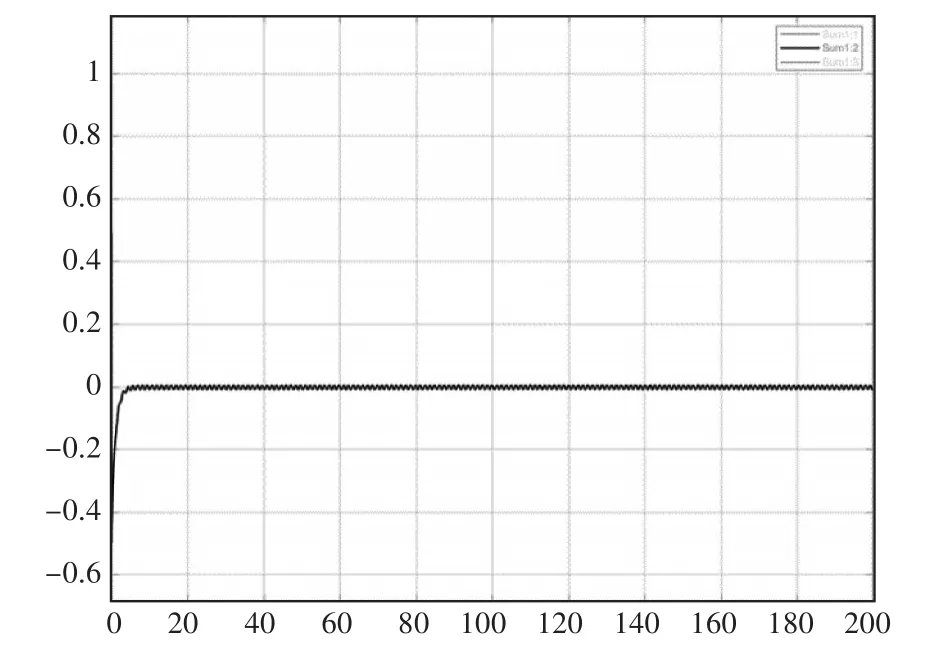
图3 滚转角状态响应

4.2 仿真分析

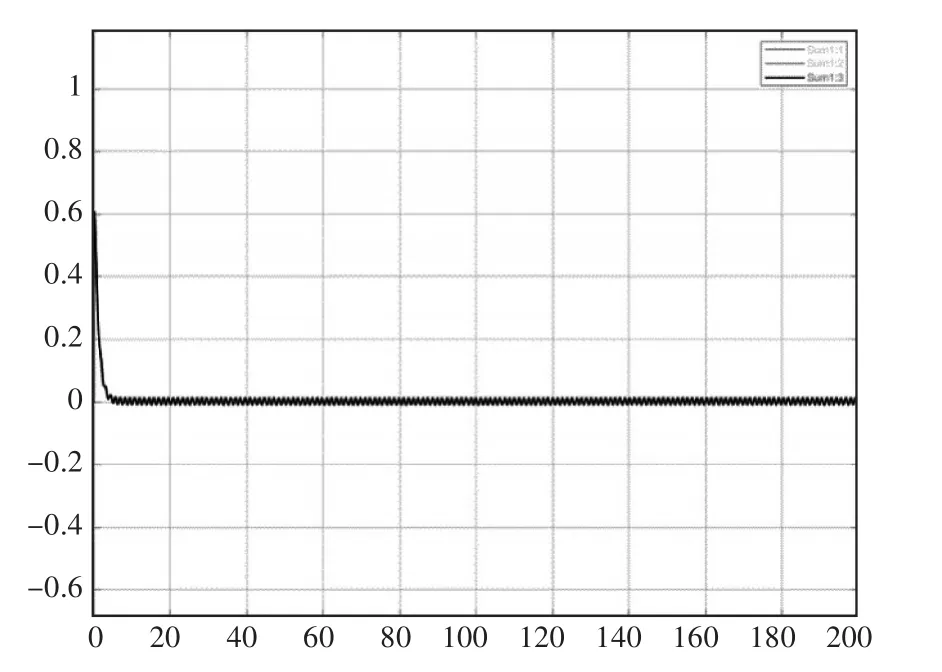
图4 偏航角状态响应

由图像可知，实施容错控制后，由于系统具有控制增益k3来补偿系统的执行器偏差和扰动带来的不良影响，从而保证了三通道的状态响应，均能在控制作用下，渐近收敛至0，这就可以说明系统故障状态，通过适当的调节，俯仰、偏航、滚转角能够恢复原来的状态，无人机依然可以保持稳定飞行，系统故障影响被逐渐补偿乃至基本消失。

5 结语

本文利用常规布局无人机非线性模型，构建含有系统故障影响的控制系统，通过设计调节自适应容错控制律，实现了对常规布局无人机的非线性容错控制。本文贯穿无人机容错控制的概念，从概述到实现仿真，对无人机的容错控制原理交代较为详细，在本文中，省去了对无人机力学与运动学建模的详细过程，推广容错控制思想与设计自适应容错控制律占据了主要篇幅，对控制律的仿真，基本实现了控制系统比较优良的性能，满足对快速性，稳定性的要求，由于具有容错性，使得该飞控系统鲁棒性较强，在无人机研究工作当中，具有一定的实际应用价值。综上所述，本文基本实现了控制目的、设计目的，理论推导有据可查，实际仿真效果真实有效。