找准学习起点才能设计好教学方案

顾艳萍

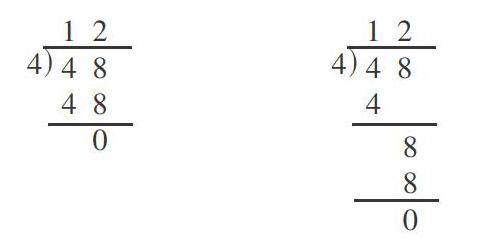
[摘要]教学设计必须符合教导功能，教学的对象是学生，要想设计出符合学生需求的教案就得找准学生的学习起点。结合教学设备、教学场地、教学手段、教学工具能有效帮助学生把握学习的起点，促使学习真正发生。

[关键词]逻辑;学习起点;设计

[中图分类号]G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020） 29-0084-02

美国教育心理学家奥苏伯尔博士说过：“影响学习的重要因素之一是学生的已有知识和经验。”教师要明确这点，并以此为依据设计教学活动。一般教材的每一章都会围绕一个主题展开讨论，话题高度集中。对此，教师在教学时，要遵循两个学习基础，一是学生知识的逻辑起点，二是学生已经积累的认知能力，然后分层挖掘学生的前概念。

一、查清知识的逻辑起点

教师在研判学生储存的前概念时，需要依据教学内容来科学预判，也就是分析学习任务。预判时，我们可以从学生完成知识技能学习后的方法进行倒推，并把方法的所有分支技能一一列出明细。以下面的四道多位数减法竖式计算为例，分析其技能进阶脉络，从①反推至④。

学习技能分解贯穿整个教学，它设定了学习新知之前应有的门槛。教师在查清了知识的逻辑起点后，还应注意与学生已有的知识进行结合，避免学生新学的内容与原有知识冲突，淡忘原有知识的情况发生。

二、查实学生学习的真正起点

1.现有的认知水平。在小学阶段，很多数学知识是呈分散混排、螺旋上升的结构。如人教版教材第四冊编排了“2-6乘法口诀求商”后，接着编排“7-9乘法口诀求商”，学生已经掌握乘法口诀求商的技巧，但是不是意味着可以绕开方法指导，直接进行习题训练呢？训练时又该如何强化？前期“2-6的乘法口诀求商”的学习成果对后续的学习有什么影响？如果有薄弱环节，是否可以强化？通过对“2-6的乘法口诀求商”的课后测试，错误集中暴露出来：6÷2=12或6÷2=4;2÷2=4或2÷2=2;6÷3=18或6÷3=3。这说明运算符号的误用和乱用是阻碍学生学习进程的绊脚石，而“2÷1=1，5÷1=1，3÷1=1，4÷1=1”的错误表明学生对涉及1的乘法口诀记忆混乱，缺乏求商练习。这给后续教学发起警报。而在进行“7-9乘法口诀求商”的45道题目的前测中，存在这些错误：18÷6=6，63÷9=4，36÷9=7. 9÷1=8，8÷8=64，48÷8=40。这些错误为后续设计练习指明了方向，提供了经验教训，提升了设计教学的前瞻性和预见性。

2.前概念的正负迁移。教师在设计教学方案时要站在学生的角度思考，考虑学生有可能遇到的困难。学生的知识储备对新学知识可能形成正迁移，促进和加速其发展，也可能发生负迁移，阻碍和制约其发展。教师应摸透前概念的正、负迁移作用，扬长避短，科学规划，合理设计教学。

如整数一级运算的知识技能对进一步学习小数一级运算产生正向迁移，甚至可以直接拿来套用，因为小数与整数的计算法则大体相同，且是十进制下的进位和借位，因此，温习旧知时可以其为跳板进行设计。但是在整数一级运算，末位对齐则数位对齐，久而久之，末位对齐代替数位对齐的思维定式就会产生负迁移，先前的惯性思维在数域发生变化后不再适用。

例如，在列竖式乘法计算中，学生因为惯用末尾对齐从低位算起这种方法，遇到因数末尾有0的特殊情况，便弃用简算法，或者丧失简算的能力。而对于商是两位数的除法竖式，首先跃人脑海的是商是一位数的表内除法，知识自动迁移，生成的却是一步到位的极简竖式（左式），不愿写详细（右式）。面对这样的负迁移，教师如何应对？

我们要联系教材。思考在教学新知识前学生知道什么，能想起多少，可能生出什么枝节，哪些储存的知识训练是可用的，哪些可能起到负迁移作用？查清实情不但可以帮助教师确定教学起点，而且对预估学习中的易混点、易错点也大有裨益。

三、摸清学生的生活经验

学生从前概念中产生一种错误的构思，这就是另类构想。这些另类构想具有杂乱性、散漫性、浅薄性和朦胧性。因为先人为主的心理，学生往往很难自我否定早已得出的结论，尽管这些想法毫无科学根据，但是他们却深信不疑。如果不推翻它，学生很难走出错误的认知，而且即使通过点拨和诱导，学生建立了正确理解，但随着时间的推移，新近构建的新知很容易消退，之前的另类构想又会死灰复燃。因为从心理学上讲，人总是容易接纳和认同那些与原有经验相匹配的内容，并保持记忆，而对那些与原有经验相对立的内容，则容易被排斥在外。

早在正式进入课堂学习之前，学生就已经通过关注日常现象，习惯体验式学习、接触式学习，形成了伪科学的前概念和简单的思维方式。这些前概念中，有些是返璞归真的天然直觉，有些是伪科学。

例如，学生认为角就是三角形、长方形或五角星等带角的图形;认为垂线就是竖直方向的线;分数的书写规则是先写分子再写分数线和分母，和读法顺序一样。

四、厘清学生的差异性

我们要充分考虑学生的年龄和心理特征，正视他们的差异性，针对差异性开展教学。

例如，一些小学课程与中学课程内容相近，如确定位置，可能性大小等。同一教学内容，如果教材的版本不同，教学目标也不同。如“角的认识”这一内容，苏教版教材安排在第四册，人教版教材则安排在第三册;“生活中的负数”在北师大版教材中被命名为“感知生活中的负数”，而在苏教版教材被命名为“负数的认识”。就算相同年级，面对不同层次的学生，目标也应分层，如“小数意义的教学”，在基础较好的班级教学时，不妨从0.1、0.01引入，让学生用自己的话说出它们的意义。在基础较差的班级教学时，不妨改换思路，放低要求，从钱币中的“元、角、分”引入，继续提供实例，充盈概念的表象，逐步抽象出数学定义。

另外，如果站在学生的立场看教材，还可以多思考几个问题。（1）学生的原始认知是什么？教学后学生应获得什么？（2）学生有无与此相关的生活经验？这些经验是什么？（3）理解难点是什么？有什么辅助理解的措施？

教学紧密围绕教师和学生的互动展开，教师只有充分了解学生才能合理设计教程和教法，才能让教与学互相促进，形成良性循环。

（责编黄露）