追本溯源 循序渐进——“向量的数量积”教学实录

解才先

(江苏省高邮中学，225600)

数形结合是数学的重要思想方法之一.著名数学家华罗庚说过:“数无形,少直观;形无数,难入微”.而向量具有代数与几何的双重身份,是数学知识的交汇点,为江苏高考八个C级考点之一,是每年高考必考内容.本文以苏教版《数学》必修4第二章第四节“向量的数量积”第一课时为课题,设计并实施了一节追本溯源、循序渐进的数学课.教学过程实录如下.

一、温故知新

师:前面我们学习了向量的概念及表示,向量的线性运算及向量的坐标表示,在向量的线性运算中,学习了向量的加法,向量的减法与向量的数乘.

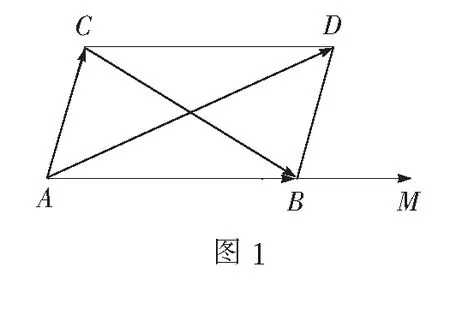
问题1向量除了与实数相乘(向量的数乘)之外,还有没有别的“乘法”呢?

设计意图孔子曰:“温故而知新,可以为师矣”.通过对已有知识的复习,既能温习旧知识,又能感受到新知识是在什么基础上发展起来的.感受数学文化循序渐进、不断发展的过程,有助于加深学生对旧知识的再理解,意识到新知识是在旧知识框架基础上发展起来的.

二、新知探索

已知一个物体在力F作用下产生的位移量为S,该力所做的功如何计算?

(1)若力F的方向与物体的运动方向相同，则W=|F||S|.

(2)若力F的方向与物体的运动方向垂直，则W=0.

(3)若力F的方向与物体的运动方向相反，则W=-|F||S|.

师:这里力F与位移S均为矢量即向量,功可以看成是由两个向量进行某种运算之后的结果,(1)中方向相同,即力与位移的夹角为0°;(2)中方向垂直,即力与位移的夹角为90°;(3)中方向相反,即力与位移的夹角为180°.三个等式又可以写成W=|F||S|cos 0°,W=|F||S|cos 90°,W=|F||S|cos 180°,这是三种角度比较特殊的情形.一般地:

(4)若力F的方向与物体的位移S的夹角为θ呢?

问题2“做功运算”能一般化成什么样的数学运算?

W=|F||S|cosθ,这里力F与位移S均为矢量，即向量.F一般化记为a,S一般化记为b,则有W=|a||b|cosθ,等式右边是三个数乘积形式,结果为数量,即左边是标量(数量),我们称之为向量的数量积.

向量的数量积可用文字表述为:已知向量a,b,它们的夹角为θ,我们把数量|a||b|cosθ称为向量的数量积(或内积),记作a·b,即a·b=|a||b|cosθ,则根据向量的数量积的文字表述,功的运算可以记为

W=|F||S|cosθ=F·S.

设计意图以学生已有知识为背景进行导入,符合学生的认知发展规律.德国教育家第斯多惠说过:“教学必须符合人的天性及其发展的规律,这是任何教学的首要的、最高的规律”.通过对已有物理知识的再学习,探索背后隐藏的数学知识,让学生感受物理数学“一家亲”,通过知识发生与发展过程的教学,使学生感受和领悟数学化过程及其思想.数学教学不是单一的教授知识,还必须关注思想、方法的渗透与能力的培养.

三、新知形成

向量数量积定义中有一句话:夹角为θ.在功的学习中我们也提到了力与位移的夹角,力与位移均为矢量即向量,下面来学习两向量的夹角.

问题3讨论探究图2中正六边形各向量的夹角:(1)a与b的夹角大小为120°.(2)a与c的夹角大小为60°.

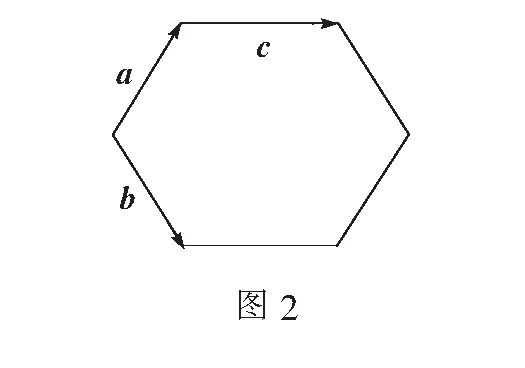
师:对于(2)，有的同学说是60°,有的同学说是120°,到底是多少呢?

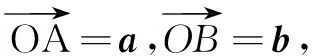
注意(1)在两向量的夹角定义中,两向量必须是“共起点”的;

(2)向量的夹角的范围为0°≤θ≤180°.

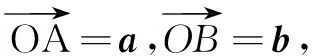
问题4上述“向量的数量积”文字表述是否精确严谨?

生:不够严谨,向量的夹角定义中指的是两个非零向量,那么这里也应该指明是非零向量,也要注明向量夹角的范围.

向量的数量积可进一步表述为:已知两个非零向量a,b的夹角为θ(0°≤θ≤180°),则称数量|a||b|cosθ为向量a和b的数量积,记作a·b,即a·b=|a||b|cosθ.

师:这就是我们这节课学习的向量数量积的定义.定义中要求是非零向量,但是学习向量的概念及其表示时,我们知道向量也包括零向量,是不是这个定义不够完美呢!为弥补这一“遗憾”,我们规定:

(1)零向量与任何向量的数量积是0,即0·a=0(等式右边的0指的是实数0)；

(2) 符号“·”在向量运算中既不能省略,也不能用“×”代替.

特别地,当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.

问题5向量的数量积运算的结果与向量的加、减、数乘运算有什么不同?

设计意图叶圣陶先生说过:“教师之谓教,不在全盘授予,而在相机诱导.”以学生为中心,以问题串为驱动,采用启发、引导、探究相结合的教学方法,让学生亲身感受数学知识逐步形成与完善发展的过程.课堂上教师不能是一味地“填鸭式”灌输,然后让学生死记硬背,而应该是让学生亲身去感悟数学、发现数学、理解数学、热爱数学.

四、 新知应用

例1已知向量a与向量b的夹角为θ,|a|=2,|b|=3,分别在下列条件下求a·b.

(1)θ=135°; (2)a∥b; (3)a⊥b.

例2已知∆ABC三边长满足AB=3,BC=4,CA=5,求

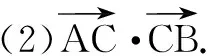
练习判断下面说法是否正确:

(1)若a≠0,则对任意非零向量b,有a·b≠0.

(2)若a·b=0,则a与b至少有一个是0.

(3)若a与b的夹角为锐角,那么a·b>0.

(注：(3)亦可变为：若a·b>0,那么a与b的夹角为锐角.)

(4)对任意的a有a2=|a|2成立.

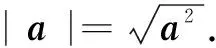
(5)任意a与b满足a·b=b·a成立.

(6)任意a,b和c满足(a·b)c=a(b·c).

我们知道，对于任意实数a,b,c,有如下运算律:

(1)a·b=b·a;

(2)(a·b)·c=a·(b·c).

请大家课后思考:向量的数量积满足哪些运算律呢?

设计意图美国著名学者布鲁纳认为:“不论我们选教什么知识,务必使学生理解知识的基本结构,这是在运用知识方面的最低要求.”通过对向量数量积定义的应用,让学生真正理解定义结构的精髓,学以致用,使其对知识的理解得到升华.一般学习完新定义之后,我们会研究它的运算律等,通过题目引出基本结构,也为下节课的学习埋下伏笔.让学生在意犹未尽中结束课堂,激发学生对数学浓厚的思考热情与学习兴趣.