Rota-Baxter q-3-李代数

林 丽 鑫

(牡丹江师范学院 数学科学学院, 黑龙江 牡丹江 157011)

目前, 关于李代数、 量子群、 Hopf代数、 量子空间的微分结构和微分算子的量子形式等研究已有许多结果[1-9]. 由于Rota-Baxter代数在概率学、 组合数学、 数论、 量子场等领域应用广泛, 因此讨论量子李代数的Rota-Baxter算子有一定的理论意义. 文献[10]给出了q-3-李代数的定义, 并对其结构进行了研究, 构造出一系列典型的q-3-李代数. 本文在文献[10]的基础上讨论q-3-李代数的权为λ的Rota-Baxter算子, 并给出Rota-Baxterq-3-李代数的定义, 从一些已知的代数结构中构造出Rota-Baxterq-3-李代数. 本文 F是特征为零的域,是整数集.

1 基本概念

定义1[10]设A是域 F上的向量空间, 如果3-元线性乘法[,,]q:A⊗3→A和映射Jq:A⊗5→F, 满足对任意xi∈A,i=1,2,3,4,5, 有

则称(A,[,,]q,Jq)为q-形变3-李代数, 简称q-3-李代数.

定义2[11]设λ∈F为固定的元素.

1) 若A为域 F上的向量空间, 〈,,〉:A⊗3→A为A的3-元线性运算, 则称序对(A,〈,,〉)为域 F上的3-元代数;

2) 如果线性映射d:A→A满足

则称d为3-元代数的权为λ的微分算子,A称为3-元微分代数;

3) 如果(A,〈,,〉)上的线性映射P:A→A, 满足对任意的x1,x2,x3∈A, 有

则称P为3-元代数的权为λ的Rota-Baxter算子. 记(A,〈,,〉,P)是权为λ的3-元Rota-Baxter代数.

定义3设(L,[, ,]q,Jq)为域 F上的q-3-李代数, 对任意的x1,x2,x3∈L, 如果线性映射P:L→L满足

则称P是q-3-李代数的权为λ的Rota-Baxter算子. 记(L,[,,]q,Jq,P)为Rota-Baxterq-3-李代数.

2 由Rota-Baxter李代数实现Rota-Baxter q-3-李代数

首先讨论由Rota-Baxter李代数(L,[,],P)实现Rota-Baxterq-3-李代数.

[xi,xj,xk]qf=q2i-j-kf(xi)[xj,xk]+q2j-k-if(xj)[xk,xi]+q2k-i-jf(xk)[xi,xj],

(5)

Jq:L⊗5→F,Jq(xi,xj,xs,xt,xr)=qs+t+r.

定理1设(L,[,],P)是权为λ的Rota-Baxter李代数,f∈L*(L的对偶空间)满足∀xi,xj∈L,f(xi,xj)=0, 则P是q-3-李代数(L,[,,]qf,Jq)的权为λ的Rota-Baxter算子当且仅当P满足∀xi,xj,xk∈L, 有

其中IdL:L→L为恒等映射.

证明: 首先， 由引理1, 对任意的xi,xj,xk∈L, 三元运算[,,]qf满足式(5), 下面证明式(6)成立：

由式(4), 得

证毕.

其次， 讨论由Rota-Baxter李代数(A,[,]k,P)实现Rota-Baxterq-3-李代数. 设A是域 F上的交换结合代数, {Lr,Mr|r∈}是A的一组基, 且具有如下乘法法则：

LrLs=Lr+s,MrMs=Mr+s,LrMs=0, ∀r,s∈.

(7)

对任意固定整数k∈, 定义A上的导子dk, 使得

dk(aLr+bMt)=arLk+r, ∀a,b∈F,r,t∈.

(8)

在A上定义乘积：

[u,v]k=dk(u)v-udk(v), ∀u,v∈A,

(9)

则(A,[,]k)是李代数.

引理2[12]设(A,[,]k)是由式(10)构成的李代数,f:A→F是非零线性函数, 且满足对任意r∈,f(Lr)=0, 则(A,[,,]fk)是3-李代数, 其中

[Lr,Ls,Mt]fk=f(Mt)(r-s)Lr+s+k, ∀Lr,Ls,Mt∈A.

(10)

定理2设(A,[,]k,P)是权为λ的Rota-Baxter李代数,dk由式(8)定义, 满足dkP=Pdk, 则(A,[,,]fk,P)是权为λ的Rota-Baxter 3-李代数当且仅当P满足

f(Mt)[P(Lr),P(Ls)]fk∈Ker(P+λIdA), ∀Lr,Ls,Mt∈A,

(11)

其中IdA:A→A是恒等映射.

证明: (A,[,,]fk)是由引理2定义的3-李代数, 则对任意Lr,Ls,Mt∈A, 有

由Rota-Baxter 3-李代数的定义, 有

证毕.

(12)

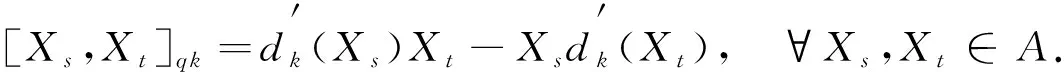
(13)

引理3[10]设f:A→F是非零线性函数, 满足对任意r∈, 有f(Lr)=0, 则对任意固定的整数k, 三元有序组(A,[,,]qfk,Jq) 为q-3-李代数, 其中∀Xi,Xj,Xr,Xs,Xt∈A, 有

[Xr,Xs,Xt]qfk=f(Xr)[Xs,Xt]qk+f(Xs)[Xt,Xr]qk+f(Xt)[Xr,Xs]qk,

(14)

Jq:A⊗5→A,Jq(Xi,Xj,Xr,Xs,Xt)=qi+k+1.

根据定理2和引理3可得：

其中IdA:A→A为恒等映射.

下面讨论由Rota-Baxter左对称代数实现Rota-Baxterq-3-李代数. 假设L是 F上的线性空间, *:L⊗L→L是2-元线性运算, 且对任意x,y,z∈L, 满足

(x*y)*z-x*(y*z)=(y*x)*z-y*(x*z), ∀x,y,z∈L,

(16)

则(L,*)称为左对称代数. 显然所有的结合代数都是左对称代数, 对任意左对称代数L, 定义运算

[x,y]*∶=x*y-y*x,

(17)

则称G(L)=(L,[,]*)为左对称代数L的伴随李代数. 如果线性映射P:L→L是左对称代数(L,*)的权为λ的Rota-Baxter算子, 即对任意x,y∈L,P满足

P(x)*P(y)=P(P(x)*y+x*P(y)+λx*y), ∀x,y∈L,

(18)

则P为其伴随李代数G(L)=(L,[,]*)的权为λ的Rota-Baxter算子.

引理4[13]1) 设(L,*)是左对称代数,P是权为λ的Rota-Baxter算子, 则P为其伴随李代数(L,[,]*)的权为λ的Rota-Baxter算子;

2) 设(L,*,P)是权为0的左对称代数, 则(L,·)是一个左对称代数, 其中

x·y∶=P(x)*y-y*P(x)+λx*y, ∀x,y∈L,

(19)

且P是(L,·)的权为0的Rota-Baxter算子;

3) 设(A,·,P)是权为λ的Rota-Baxter交换结合代数,D是(A,·)的导子, 且满足DP=PD, 则(A,*,P)是权为λ的Rota-Baxter左对称代数, 其中对任意x,y∈A, 有

x*y=D(x)·y,

(20)

所以可得Rota-Baxter李代数(A,[,]*), 其中

[x,y]*=D(x)·y-D(y)·x, ∀x,y∈A.

(21)

下面在线性空间A上定义3-元乘积[,,]fq*, 对任意xi,xj,xk∈A, 有

[xi,xj,xk]fq*=q2i-j-kf(xi)[xj,xk]*+q2j-k-if(xj)[xi,xk]*+q2k-i-jf(xk)[xi,xj]*,

(22)

Jq:A⊗5→F,Jq(xi,xj,xs,xt,xr)=qs+t+r.

显然(A,[,,]fq*,Jq)是q-3-李代数.

根据引理4和定理1可得：

定理4设(A,*,P)是权为λ的Rota-Baxter左对称代数, 对任意的xi,xj,xk∈A,i,j,k∈,f∈A*满足f(xi*xj-xj*xi)=0, 则P是q-3-李代数(A,[,,]fq*,Jq)的权为λ的Rota-Baxter算子当且仅当

其中IdA:A→A为恒等映射.

3 由Rota-Baxter群代数实现Rota-Baxter q-3-李代数

引理5[10]设(G,+)是Abel群, F[G]是群代数,α∈Hom(G,F+). 则(F[G],[,,]q,Jq)是q-3-李代数,I0是q-3-李代数(F[G],[,,]q,Jq)的极大理想, 其中对任意fg,fh,fu∈F[G], 有

[fg,fh,fu]q=q-α(u)(α(u-h)fh+u-g+α(g-u)fg+u-h+α(h-g)fg+h-u),

(24)

Jq(fs,ft,fg,fh,fu)=qα(g)+α(h)+2α(u).

由引理4和引理5, 设(F[G],·,P)是权为λ的Rota-Baxter群代数,α*: F[G]→F[G] 为(F[G],·)的导子, 满足

α*P=Pα*,ωα*+α*ω=0,

则(F[G],*,P)是权为λ的Rota-Baxter左对称代数, 其中对任意fh,fu∈F[G], 满足

fh*fu=fh·α*(fu).

(25)

因此(F[G],[,]*)为Rota-Baxter李代数, 其中

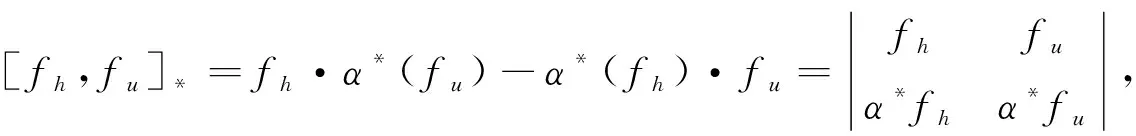
(26)

从而

[P(fh),P(fu)]*=P([fh,P(fu)]*+[P(fh),fu]*+λ[fh,fu]*),

(27)

即

定理5设(F[G],[,]*,P)是权为λ的Rota-Baxter李代数, 则P是q-3-李代数(F,[,,]q,Jq)的权为λ的Rota-Baxter算子当且仅当对任意的fg,fh,fu∈F[G],P满足

(29)

其中IdF[G]: F[G]→F[G]为恒等映射.

证明: 根据引理5, 对任意fg,fh,fu∈F[G], 有

证毕.