半无限极大极小离散化问题的一个非单调SQCQP算法

杨永亮, 王福胜, 甄 娜

(太原师范学院 数学系, 山西 晋中 030619)

0 引 言

极大极小(Minimax)优化问题[1-3]是一类重要的优化问题, 目前已取得丰富的研究成果. 半无限极大极小问题作为其特殊形式广泛应用于工程设计、 最优控制、 金融工程等领域. 由于其特殊的结构, 大多数传统方法不再适用, 离散化方法[4-5]是求解该类问题的重要数值方法之一.

半无限极大极小问题具有如下形式:

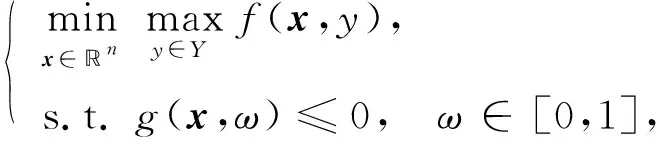
(1)

其中: 指标集Y={1,2,…,m};f:n×Y→和g:n×[0,1]→关于x连续可微. 将[0,1]离散成有限集：Ω={0,1/q,2/q,…,(q-1)/q,1}, 其中q反映了离散水平,q越大离散水平越好. 基于离散化方法求解原问题(1)可归结为求解一系列具有如下形式的半无限极大极小离散化问题：

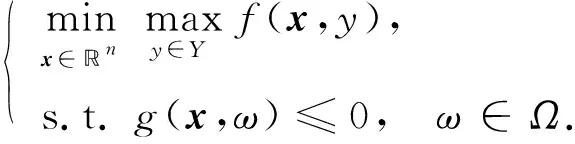
(2)

本文主要考虑具有固定离散水平q的极大极小优化问题(2). 序列二次约束二次规划(SQCQP)算法[6-7]是继序列二次规划(SQP)算法后又一类求解约束优化问题的重要方法, 每一步迭代只需求解一个二次约束二次规划(QCQP)子问题, 子问题的近似程度比二次规划(QP)子问题更高, 迭代次数比SQP算法更少, 不需要任何修正方向即可克服Maratos效应, 因此得到广泛关注. 由于求解一般QCQP子问题无法保证得到的下降方向是可行的, 因此为了解决该问题, 常见的方法是将子问题得到的下降方向与找到的可行方向相结合以得到可行下降方向, 或对原下降方向进行修正, 但这两种方法都会增加计算工作量. 针对该不足, 文献[5]提出了一类模松弛强次可行算法, 该类算法具有初始点可以任取, 且只需要求解一个子问题即可得到可行下降方向的优点. 在模松弛强次可行方向法中常利用单调线搜索得到步长, 其缺点是当迭代点“陷入很窄的峡谷时”, 常会导致小步长或出现锯齿现象, 而非单调线搜索技术可有效克服这些缺点. 受Zhang等[8]非单调技术的启发, 本文构造一个新的非单调线搜索, 并将其应用于算法构造中. 基于文献[4-5,7-8], 本文充分利用模松弛强次可行算法的思想和非单调技术的优势, 给出一个半无限极大极小离散化问题的非单调SQCQP算法.

1 算法描述

定义问题(2)的可行集为F={x∈n:g(x,ω)≤0,ω∈Ω}, 求解问题(2)等价于求解如下问题:

(3)

(4)

为叙述方便, 记

Ω-(x)={ω∈Ω|g(x,ω)≤0},Ω+(x)={ω∈Ω|g(x,ω)>0},

Ω-(xk)={ω∈Ω|g(xk,ω)≤0},Ω+(xk)={ω∈Ω|g(xk,ω)>0},

构造QCQP子问题:

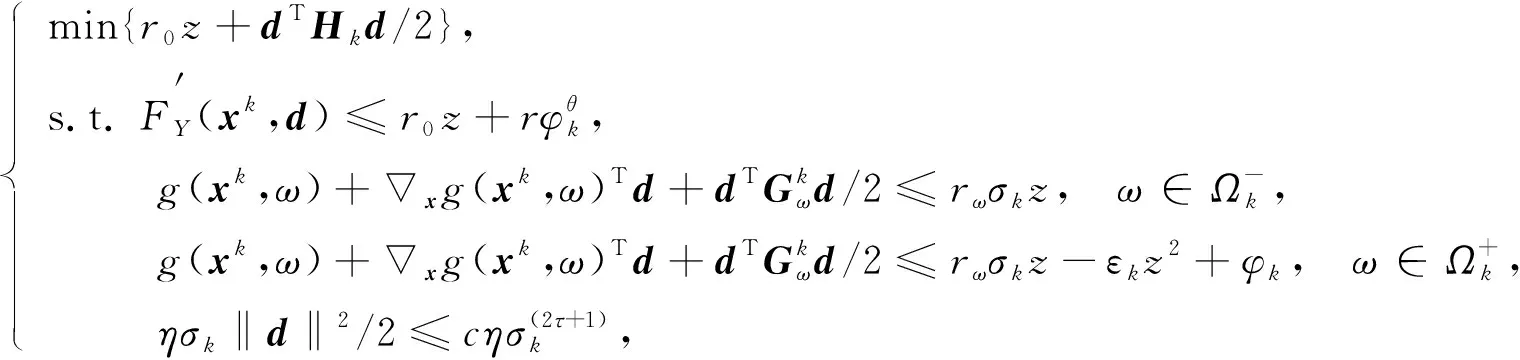
(5)

注1在式(5)中引入一个重要项-εkz2, 是为了确保当dk→0时有zk→0. 子问题(5)的最后一个不等式约束并没有消去因子σk, 主要是为了方便表达其相应乘子的有界性假设. 没有消去η, 是为了保证问题(3)和(4)较弱的假设.

设(zk,dk)是子问题(5)的一个KKT(Karush-Kuhn-Tucker)点, 存在乘子μk∈,νk∈,uk∈n满足如下KKT条件:

假设:

(H1) 对任意的y∈Y,ω∈Ω, 函数f(·,y)和g(·,ω)均连续可微;

(H2) 对任意的x∈n, Mangasarian-Fromovitz约束规格成立(简称MFCQ成立), 即存在d∈n, 使得xg(x,ω)Td<0, 对所有的ω∈Ω成立.

引理1[7]若假设(H1)成立, 则:

1) QCQP子问题(5)总有一个最优解;

2) (zk,dk)是子问题(5)的最优解当且仅当其为子问题(5)的一个KKT点.

引理1表明QCQP子问题有良好的性质.

引理2[7]若假设(H1),(H2)成立, (zk,dk)是子问题(5)的最优解, 则:

1)r0zk+(dk)THkdk/2≤0,zk≤0;

2)zk=0 ⟺dk=0;

3)zk=0 ⟹xk是QCQP问题的一个Fritz John点;

4) 如果xk∉F, 则zk<0;

5) 若dk≠0, 则zk<0,dk为问题(2)在xk处的强次可行下降方向.

本文在Zhang等[8]提出的非单调准则的基础上进行改进, 得到修正的非单调线性搜索准则如下：

其中:δ1∈(0,1/2),δ2>0,t∈(0,1),αk为{1,t1,t2,…}中满足式(12)的最大值;ηk-1∈[ηmin,ηmax],ηmin∈[0,1),ηmax∈[ηmin,1]为参数.

算法1

步骤1) 初始化. 取适当大的正整数q(一般q≥100)将区间[0,1]离散成有限集Ω, 选取参数r,r0,rω(ω∈Ω),θ∈(0,1),τ,δ1∈(0,1/2),δ2>0,t∈(0,1),η≥0. 选取初始点x0∈n, 对称正定矩阵对称半正定, 并令k∶=0.

步骤2) 求解QCQP子问题. 对当前的迭代点xk, 求解QCQP子问题得到一个KKT点对(xk,dk,μk,vk,uk). 如果zk=0, 则xk是问题(3)的一个稳定点, 停止.

步骤3) 线搜索. 由新的非单调线搜索(12)得到步长αk.

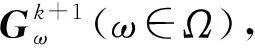
更新QCQP子问题的参数σk为σk+1.

步骤5) 令k=k+1, 返回步骤2).

2 收敛性分析

下面分析算法的全局收敛性, 若算法经过有限次的迭代终止于xk点, 则xk是问题(2)的一个Fritz John点. 假设算法1产生一个无穷点列{xk}, 下面证明{xk}的每个聚点x*都是问题(2)的一个KKT点, 为此做如下假设：

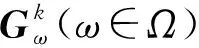
2) 矩阵序列{Hk}一致正定, 即存在两个正数a和b, 使得a‖d‖2≤dTHkd≤b‖d‖2, ∀d∈n;

(H4)f(x,y)在水平集l0={x∈n|f(x,y)≤f(x0,y)}内有下界, 函数在包含l0的开凸集S上Lipschitz连续, 即存在常数l>0, 使得

(H5) 问题(2)在{xk}的每个极限点x*处都满足扩展的MFCQ条件, 即存在一个向量d∈n, 使得xg(x*,d)Td≤0, ∀ω∈Ω0(x*).

定义子问题(5)的积极约束集[4]ω0如下：

由于子问题(5)积极约束集ω0是指标集Ω的子集, 即存在一个无限指标集K, 使得

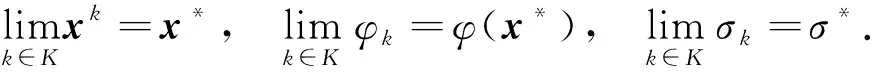
(15)

证明： 由KKT条件(7)可知,

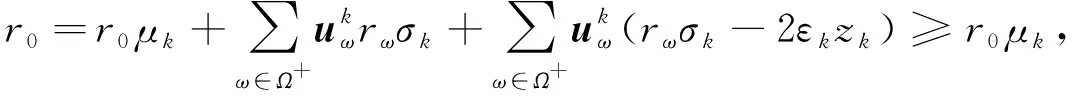
(16)

式(16)表明0≤μk≤1, 故序列{μk}有界.

引理4[8]算法产生的序列{xk}满足：

FY(xk)≤Ck,

(17)

Qk+1≤k+2.

(18)

证明: 由非单调线搜索规则式(12)知,

由递推式(13),(14), 有

由ηmax<1可知,

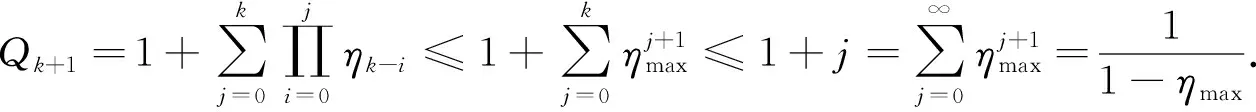
(20)

由子问题(5)的第一个约束、 假设(H1)和引理2可知, 存在一个常数M(取M>0), 使得

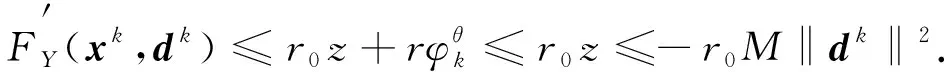
(21)

由式(19)～(21)可知,

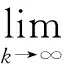
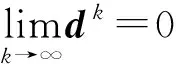
定理1若假设(H1)～(H3),(H5)成立, 则算法1或有限步终止于QCQP问题的一个Fritz John点, 或产生一个无穷迭代序列{xk}, 使得其每个聚点x*都是子问题(5)的一个KKT点.

证明： 类似文献[7]中定理3.3.1的证明. 若算法1有限步终止于第k步, 则由步骤2)和引理2可知,xk是问题(2)的一个Fritz John点. 首先假设算法1产生一个无限迭代序列{xk}, 且x*是{xk}的一个聚点. 由引理5和式(15), 不失一般性, 设存在一个无限指标集K, 使得

(22)

首先证明乘子序列

(23)

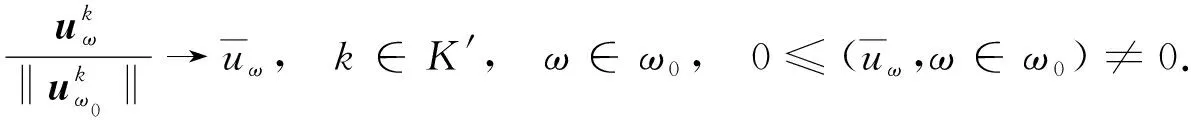
(24)

在式(23)中对k∈K′和k→∞取极限, 并结合假设(H3),(H4)及引理3, 有

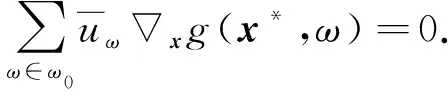
(25)

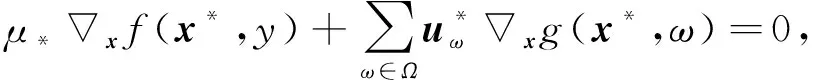
(26)

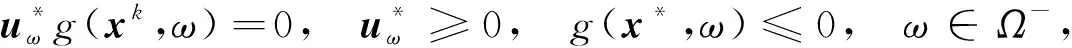
(27)

(28)

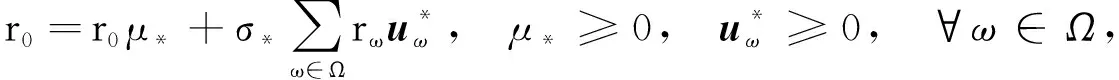
(29)

μ*rφ(x*)θ=0.

(30)

根据式(29)可知(μ*,u*)≠0, 进而由假设(H5)和式(26)～(30)可知μ*>0, 故由式(30)可得φ(x*)=0, 再结合式(26)～(30)可知x*是问题(2)的一个KKT点.

3 数值实验

下面对算法1的有效性进行数值实验, 在MATLAB 2016a上编程实现, 利用文献[1]中算例P1,P2,P3:

表1 两种算法的数值结果

由表1可见, 在选择相同的初始点, 离散水平q=100的情形下, 将采用非单调线搜索技术的SQCQP算法1与传统采用Armijo线搜索的SQP算法2进行比较, 算法1在迭代次数和计算时间上有明显优势, 同时迭代求解问题使用的约束个数也略有减少. 因此, 非单调类SQCQP算法在计算成本方面明显低于传统的SQP算法, 计算效率也得到提高. 在精度要求较低的情况下, 非单调类SQCQP算法能在提高计算效率的同时缩减计算成本, 有一定的有效性和可行性, 在较大规模非线性半无限规划问题的求解中有一定的应用价值.