基于全息挠曲线的钢桁-混凝土组合梁损伤识别
2020-09-27张鑫周志祥冯麟邵帅邓国军
张鑫 周志祥,2 冯麟 邵帅 邓国军
(1.重庆交通大学土木工程学院,重庆 400074;2.省部共建山区桥梁及隧道工程国家重点实验室,重庆 400074)
钢桁-混凝土组合结构梁桥逐渐成为组合结构桥梁的发展趋势[1],在长期运营过程中,通过损伤识别可以评估桥梁健康状况并给出合理的加固维修建议[2]。损伤识别是通过分析与结构性能相关的特征参数来判断结构整体或局部是否受到损伤[3-5],以及损伤范围与程度,从而评估结构剩余承载能力[6]。作为桥梁损伤识别的重要参数,桥梁挠度能直观反映结构形变情况[7]。桥梁挠度测量主要分为人工测量与自动测量。人工测量使用位移计、全站仪、精密液位计等,技术成熟,精度相对较高,但操作繁琐,效率低,且影响交通,不适用于桥梁长期挠度监测[8]。自动测量中的GPS位移测量简便且对交通影响小,但在竖直方向测量精度低且易受卫星信号影响[9]。基于激光光斑[10]、光电成像[11]等自动测量方法在一定程度上提高了测量精度,但在测量范围、测量环境、成本控制等方面存在缺陷。
本文对一片钢桁-混凝土组合梁开展无损及多种有损工况下的试验研究,利用一种新的视觉测量装置实现对荷载作用下桥梁全息挠曲线的非接触式实时自动无损监测,并将试验数据作为“输入”以验证损伤识别的可行性与有效性。
1 全息挠曲线的获取
视觉测量装置(图1)以现代全景视觉传感器技术、模式识别技术与计算机技术为基础,其核心系统由主动式视觉传感器、自动巡航远程控制平台、环境监测单元以及信号传输通信单元组成。

图1 视觉测量装置具体构造
桥梁全息挠曲线视觉测量方法结合了近景摄影测量和结构图像边缘轮廓线叠差技术[12-13],主要流程见图2。
结构图像边缘轮廓线叠差分析的理论公式为

式中:Δt(x)为桥梁在t时刻加载时距离原点x长度截面处的挠度;S1(x)为t时刻加载时桥梁下边缘轮廓线;S0(x)为桥梁处于无损状态时无载工况下的桥梁下边缘轮廓线,如图3所示。
获取图像像素距离与实际距离的摄影比例尺,标定段总像素距离Pd与标定段总实际距离Ad的关系式为
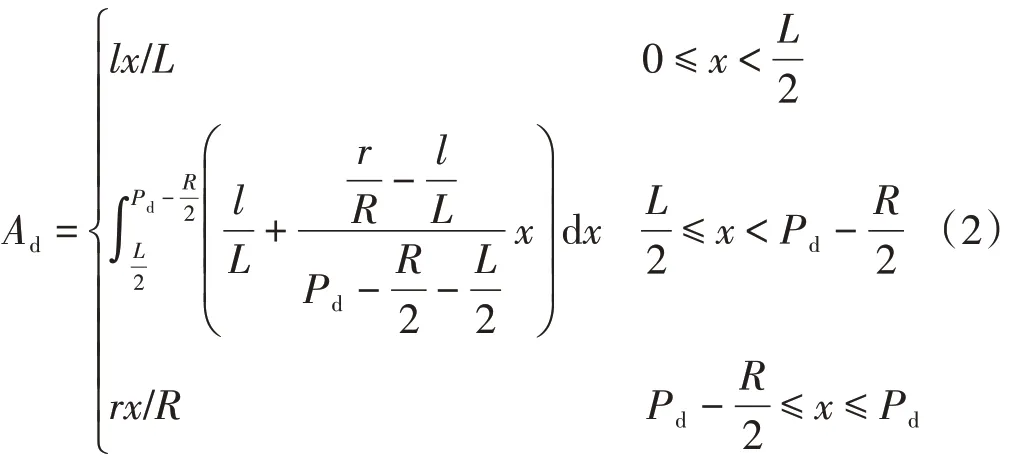

图2 桥梁全息挠曲线测量流程
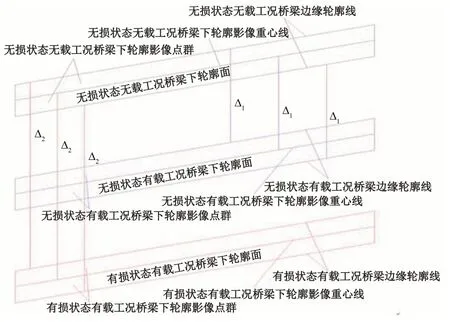
图3 桥梁边缘轮廓线叠差示意
式中:l为梁最左端到邻近标定点的实际距离;L为梁最左端到邻近标定点的像素距离;r为梁最右端到邻近标定点的实际距离;R为梁最右端到邻近标定点的像素距离;x为叠差像素距离。
2 损伤识别理论模型
利用视觉测量装置获取不同位置荷载作用下(图4)桥梁的全息挠曲线,经过数据重构可得到各截面的挠度影响线(图5)。

图4 准静力加载示意

图5 全息挠曲线数据重构图
由图5 可知,获取沿结构跨度不同荷载位置的m个全息挠曲线后,截取任意截面对应的m个荷载位移,通过数据重构可获取全截面的挠度影响线。
将全截面的挠度影响线作为“输入”,依次建立各截面与其他截面挠度影响线列向量的数据相关关系并构造Hankel矩阵,即

式中:i,j为截面位置数;k为试验次序为i号截面与j号截面第k次试验挠度影响线列向量的协方差;为i号截面与其他截面挠度影响线列向量的协方差矩阵数据序列构造的 Hankel 矩阵分别为钢桁梁i号和j号截面处第k次试验所得的挠度影响线列向量;N为加载截面数,当N为偶数时,m=N/2+1,n=N/2,当N为奇数时,m=n=(N+1)/2。

式中:为对角矩阵矩阵的第j个奇异值矩阵的第j个列向量矩阵的第j个列向量;为在第k次试验时,i号截面与j号截面挠度影响线所构造的Hankel矩阵。
矩阵的欧式范数为

式中:Λi为T次试验下矩阵奇异值的算术平均值所构成的矩阵;T为相同时间内总试验次数;λimax为最大奇异值。
结合式(8)和式(9)求解全截面损伤识别指标:

式中:λ为全截面最大奇异值;λ'为全截面最大奇异值的斜率;λ″为全截面最大奇异值斜率的变化率;x0为某一截面位置;h为步长,即相邻截面之间的距离。
3 钢桁-混凝土组合梁受载试验
3.1 试验梁组成材料与构造
制作一片纵向长度为7 160 mm 的钢桁-混凝土组合梁,基于视觉测量装置获取其全息挠曲线并进行损伤识别。其材料组成见表1。

表1 试验梁材料
组合梁计算跨径为7 000 mm,总高度为770 mm。其中,混凝土桥道板高140 mm,钢桁梁底宽330 mm;钢桁梁弦杆截面形式为Π 形,腹杆截面形式为槽形,其构造形式及立面布置见图6。

图6 钢桁-混凝土组合梁
3.2 加载与测量设备
采用百分表和视觉测量装置分别获取组合梁的挠曲线,安装应变片以限制加载最高值。百分表布置与试验梁加载顺序如图7所示。
通过设置滑动支座与铰支座使组合梁为简支梁受力模式,加载装置采用电控油压千斤顶向下加载。加载前依次对组合梁钢桁斜杆进行焊割工作以模拟杆件损伤工况(表2),损伤范围为损伤斜杆至试验梁最左端的距离。工况4 是在试验梁损伤4 根斜杆的基础上焊接修复2根损伤范围为20~25 dm的斜杆。
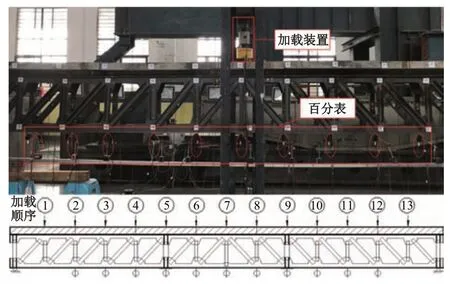
图7 百分表布置与试验加载顺序
3.3 测量结果
在组合梁无损状态下,将40~320 kN 荷载作用下的边缘轮廓线与未加载状态下的边缘轮廓线进行叠差,经过像素点距离与实际距离的转换后得到组合梁的全息挠曲线,如图8(a)所示。百分表测得的不同荷载作用下组合梁挠度曲线如图8(b)所示。

表2 斜杆损伤工况
由图8 可知:全息挠曲线线性饱满且符合结构变形连续与平滑的特点;相比于百分表挠度曲线,基于视觉测量的全息挠曲线测点数呈指数倍数(千级)增加,更加符合结构变形后曲线的整体性、连续性与协调性,可以减少百分表测得的挠度曲线因测点数稀疏带来的拟合曲线误差累积问题。2 种测量方式所测得的挠度值最大误差、平均误差及平均误差率分别为1.62 mm,0.34 mm 和3.0%,精度满足工程要求。因此,基于视觉测量的方法能够对结构损伤进行识别。
4 损伤识别结果及分析
奇异值表征截面处的奇异信号强弱。结构局部刚度的折减必然使超静定结构组合梁发生应力重分布,进而增强各截面的奇异信号,其数值随着损伤程度的增加而增加。为验证损伤识别的可行性与有效性,利用无损及多种有损工况下试验梁的全息挠曲线数据,结合MATLAB 主控程序编写的损伤识别算法,计算组合梁在多种工况下的全截面挠度影响线奇异值及其斜率和斜率变化率,见图9。
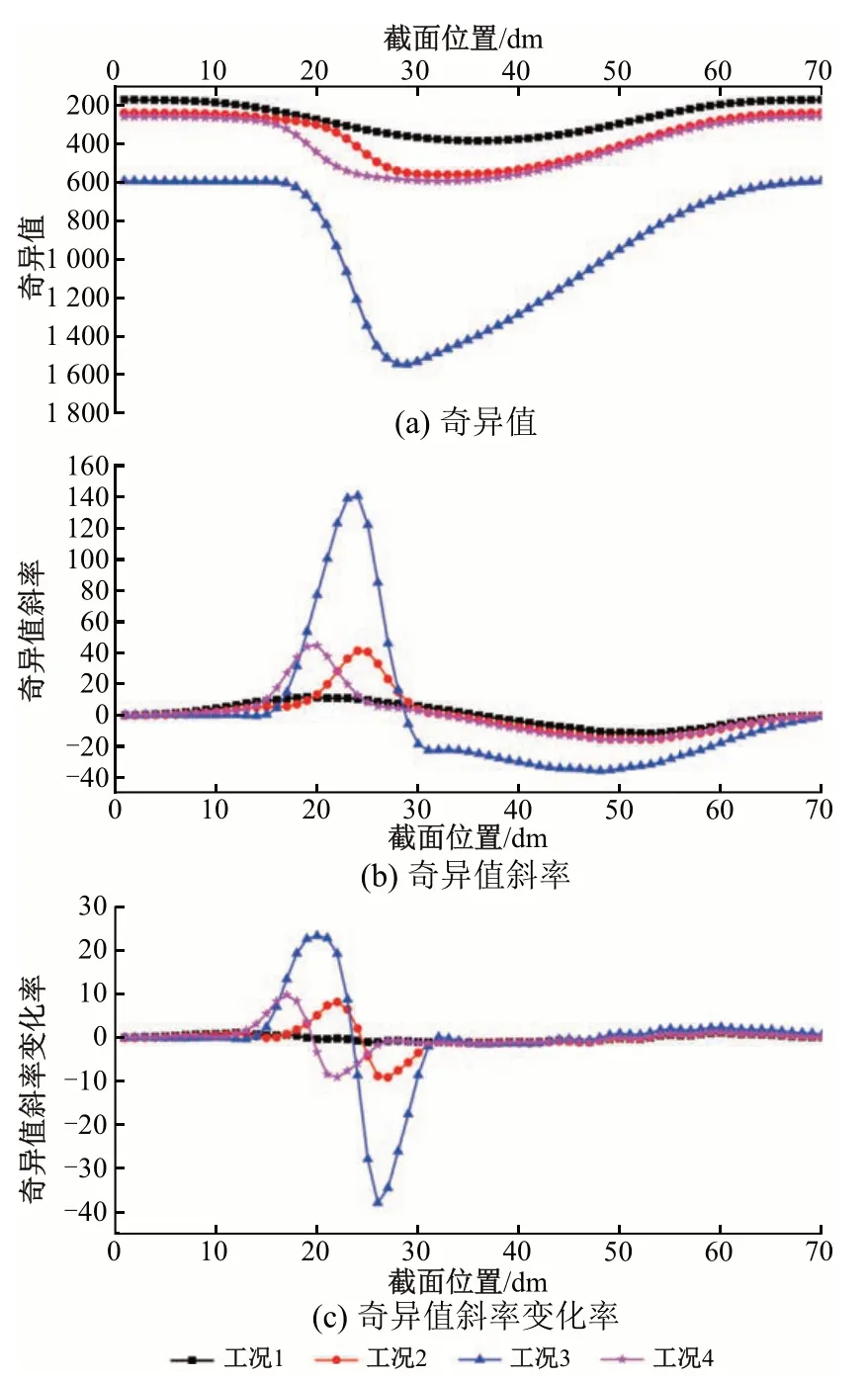
图9 不同损伤工况下组合梁的损伤识别指标
由图9(a)可知,工况2—工况4 中各截面奇异值均大于工况1,说明这3 者为损伤工况;工况3 各截面奇异值远大于工况2和工况4,可以判定工况3 的损伤程度较大,这与人为设计的损伤结果一致。因此,可依据奇异值大致判断损伤程度。
由图 9(b)与图 9(c)可知:工况2—工况 4 均有较大突变峰值,当结构为无损状态时各截面斜率变化率理论上应为0,若对应损伤识别指标不为0或产生正负突变点,则说明该截面可能出现结构损伤,且峰值随损伤程度的增加而增加。
损伤识别指标与范围见表3。对比图9(c)与表3可知:工况2 的正突变点由19 dm 处开始,到30 dm 处结束,说明在19~30 dm 可能存在损伤,对应人为损伤2 根连接范围为20~25 dm 的斜杆工况,相应斜率峰值为41.31;工况3的正突变点由14 dm 处开始,到31 dm处结束,说明工况3 的损伤范围大于工况2,其对应斜率峰值为140.12,说明其损伤程度远高于工况2。工况4 斜率峰值比工况2 略有增大的原因是修复2 根斜杆的位置仍存在一定初始微损伤。因此,利用奇异值斜率峰值与斜率变化率突变范围可对损伤范围及程度进行有效识别与判断。

表3 损伤识别指标与范围
5 结论
本文提出一种基于全息挠曲线的损伤识别方法,并对一片钢桁-混凝土组合梁开展了无损及多种损伤工况下的受载试验,得到结论如下:
1)与百分表测量的挠曲线相比,基于桥梁实时数字图像获取的全息挠曲线线形饱满且测点多,符合结构变形的连续协调性,且测量精度满足工程要求,可将其运用于桥梁的损伤识别中,以增加结构局部形变异常信息的捕捉。
2)利用本文损伤识别方法对4种不同损伤工况的试验梁进行分析,其识别结果的范围和程度与加载前人为设计的损伤结果大致相同,验证了该方法的可行性与有效性,表明基于全息挠曲线的损伤识别方法能有效识别出结构的损伤位置与损伤程度。
