一种针对短波多径信道的频移估计算法*

刘世洪，夏洪君，颜浩洋

（重庆金美通信有限责任公司，重庆 400030）

0 引言

短波通信具有经济性、灵活性、适应性及抗摧毁性，在军事通信中广泛应用，即使在微波通信、卫星通信等通信手段快速发展的今天，也被持续关注和不断发展。战争情况下，复杂电磁环境和通信双方可能存在的移动性，使短波信道存在着严重的多径、衰落、多普勒频移等影响[1]。因此，需要研究针对多径信道条件下的参数估计，以评估多径信道对短波通信的影响，从而选取合理的参数，保证短波可靠通信的传输。

通常，在多径衰落信道条件下的信道参数估计主要包括多径数、多径时延、频偏、展宽等，其中多普勒频移会导致接收信号中有用的信号成分功率衰减[2]，特别是对PSK、QAM 调制来说，频移会导致数据符号相位旋转与扩散，影响数据信息正确解调，系统误码率增大[3]。因此，需要在接收端对频移进行有效的估计，以修正其对接收信号的影响，提高接收机性能。本文针对多径信道条件下的频偏估计问题展开研究，在设定所有路径上频移相等的条件下，根据多径时延的估计范围进行划分，利用延时抽头线结构对接收训练序列进行等效，并对多径信道下的频移的最大似然估计进行推导，该方法主要应用在短波通信中信号受到多径干扰时的频率估计。

1 短波调制解调数学模型

在短波通信系统中，调制端经由帧组成、成形滤波、子载波正交调制三个部分完成，其原理框图如图1 所示。

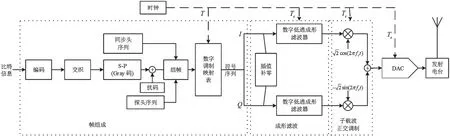
图1 短波突发通信系统调制端

①帧组成：根据设定帧格式，将用户比特信息组帧并调制成数字符号，生成的传输符号序列表示为x=[x0,x1,…,xL-1]，总长度为L。

②成形滤波：将传输符号序列转化为基带信号，设定符号周期为T，发送端采用平方根升余弦滤波器gT(t)作为成形滤波器[4]，则基带信号可表示为

③子载波正交调制：对基带信号sl(t)进行子载波正交调制，得到

式(2)中，Re{·}表示取实部运算，fc表示子载波频率，将s(t)输出给电台即可进行射频信号发送，完成信号调制过程。

当信号通过多条路径传播抵达接收端时，每条路径分别受到信道时延、时延扩展、幅度衰落及多普勒频移的影响，信道模型[5]为

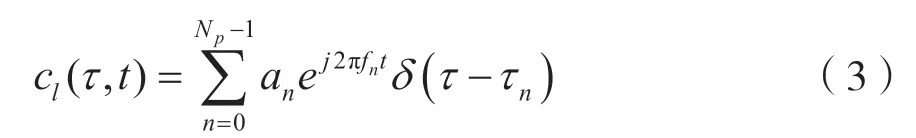
式（3）中，Np表示路径数，其中n表示路径索引，fn表示多普勒频移，τn表示时延，an=Ane jθn为复数，其中An为信道带来的幅度衰落及时延扩展的影响，θn表示信号时延带来的相位偏差，其均匀分布于[-π,π]之间。因此，接收基带信号可以表示为

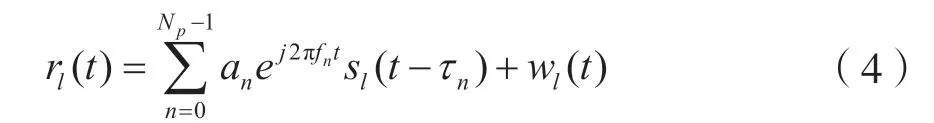
同时，将式（3）带入式（4）后，rl(t)可以表示为

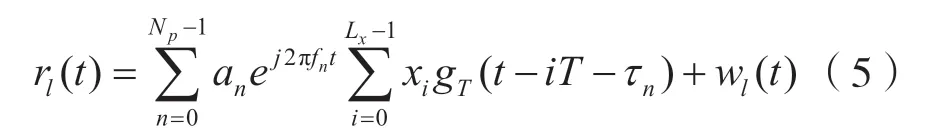
rl(t)经过DAC 采样后，经过匹配滤波器，输出y(kTs)可表示为：

然后利用滑动时间窗对y(kTs)采样，即以τu=iuTs为起始时刻，每间隔符号时间周期T进行采样，采样帧长度为Lx，则采样的符号序列可表示为

其中yk可表示为

之后利用对y(t)进行信号同步、多径估计、频率估计等，其中频偏估计即是本文的主要研究内容。

2 多径信道条件的频率估计

在短波通信中，相对于电离层运动及收发双方相互运动导致的多普勒频移，收发双方之间电台振荡器导致的载波频移数量级较大[6]，因此，本节中设定所有的传播路径上频移相等，式（7）可转换为：

此时，可得到频率的粗估计结果为Fm，之后进行q次二分搜索[12]迭代即可获取精确的频率估计，框图结构如图2 所示。

图2 多径信道下的频率估计

2 仿真与性能分析

为了验证多径信道条件下频移估计算法的可行性及理论分析的正确性，本节对上述频率估计算法进行蒙特卡洛实验仿真性能分析与比较，仿真中训练序列调制方式为8PSK 序列，长度为96，信道条件中，ac=Ace jθc，其中Ac为实数，服从均值为0，方差为1 的高斯分布，θc均匀分布于[-π,π]，对每一帧信号而言ac为固定值，成形滤波器与匹配滤波器采用滚降系数为0.4 的平方根升余弦滤波器。

通过Nmc=10000 次蒙特卡洛实验得到MSE 性能，计算方式如下：

其中，Fs为设定的频移，为第i次试验的估计值。

仿真1：设定DFT 长度N=256,512，δ均匀分布于区间[-1/2,1/2]，在SNR 为-10～15 dB 条件下对本文频率估计算法进行MSE 性能仿真，仿真结果如图3 所示。仿真结果表明：当取q=0，在SNR为-3dB 时，MSE 性能开始趋于平滑，当q为2 或3 时，在6dB 时MSE 性能逼近CRLB；而取DFT 长度为N=512 后，MSE 性能有大幅度提升，当q=0，在SNR 为-5dB 时，MSE 性能开始趋于平滑，当q=2,3 时，MSE 性能在-3dB 时即可逼近CRLB。

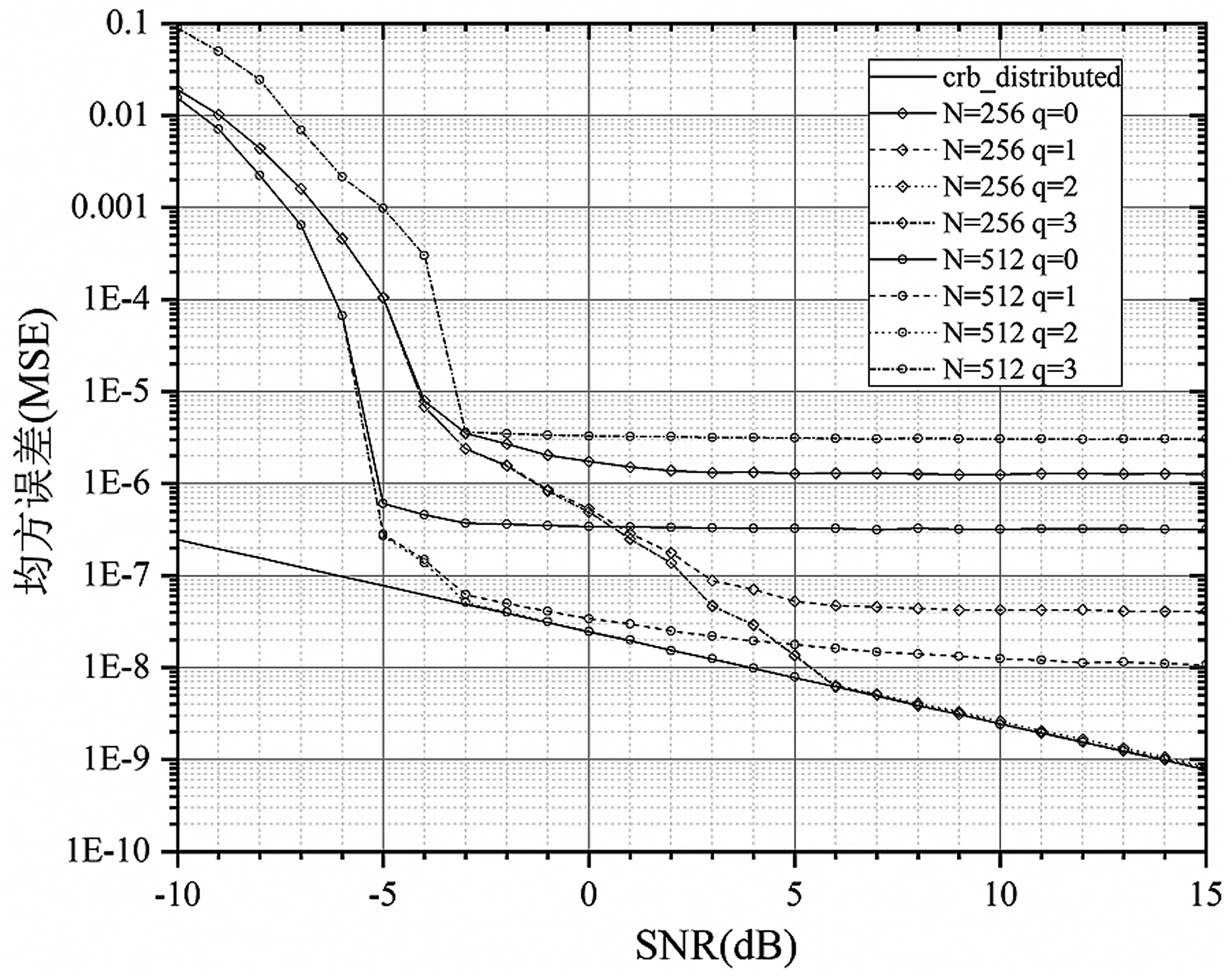
图3 仿真1 的算法性能

仿真2：采用Watterson 信道模型，信道参数如表1 所示，两条路径等能量，取fsmin=fs，设定fsT均匀分布于[-0.01,0.01]，δ均匀分布于区间[-1/2,1/2]，其中算法使用长度N=512 的DFT，在SNR 为-10～15dB 条件下对频率估计的MSE 性能进行仿真，蒙特卡洛实验次数为Nmc=10000，仿真结果如图4 所示。

图4 仿真2 的算法性能

仿真结果表明：取P1=0.02 与P1=0.5 时性能相当，当取迭代次数q=0,1，在SNR 为2dB 时MSE性能开始趋于平滑，当q=2,3，在2dB 时MSE 性能逼近CRLB。

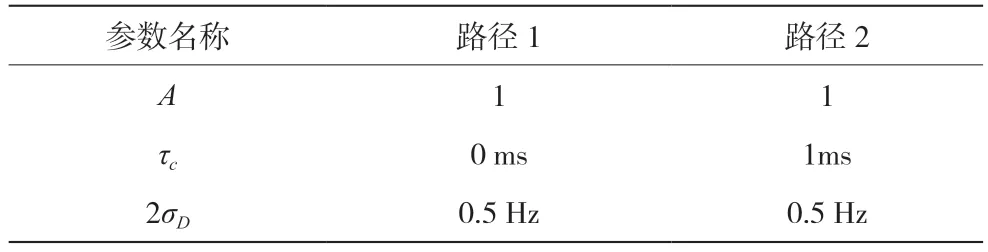
表1 ITU-R 中等信道传播路径参数

3 结语

针对短波多径信道条件下的频率估计算法主要应用于信号精确同步后，本文根据多径时延的估计范围进行划分，利用延时抽头线结构对接收训练序列进行等效，并对多径信道下的频移的最大似然估计进行推导。仿真结果表明，在ITU 中等信道条件下，SNR 为2dB 时MSE 性能可逼近CRLB，适用于短波通信中信号受到多径干扰时的频率估计。