MIMO 电力线载波通信中基于压缩感知的信道与脉冲噪声联合估计方法*
2020-09-27党三磊吴倩文
赵 闻,张 捷,李 倩,党三磊,吴倩文,路 韬
(1.广东电网有限责任公司计量中心,广东 广州 510080;2.北京邮电大学,北京 100876)
0 引言
电力线通信(Power Line Communication,PLC)是一项使用电力线传输数据信号的技术。因为电力线系统具有线路分布广泛、安装成本低廉等优势,在智能电网、家庭自动化、办公自动化等领域中被广泛应用,被认为是一种重要的通信方式[1-2]。为了加速PLC 的发展,将多输入多输出(Multiple-Input Multiple-Output,MIMO)技术引入,以进一步提升系统性能。MIMO-PLC 系统利用多个传输信道,可以提供更大的信道容量和更高的数据速率[3-4]。
信道状态信息(Channel State Information,CSI)的准确性将直接影响MIMO-PLC 系统的整体性能,因此精确的信道估计技术是保证通信质量的关键。然而,电力线网络的负载与拓扑结构非常复杂,导致PLC 信道中噪声的组成和变化也很复杂[5-7],其中脉冲噪声(Impulse Noise,IN)的存在使传统信道估计技术的性能降低。因此,在具有IN 的情况下对MIMO-PLC系统进行精确的CSI采集至关重要。
基于导频的信道估计一直是热点研究方向,其中压缩感知(Compressed Sensing,CS)理论将信道估计转换为稀疏信号的重构问题,可以有效利用信道的稀疏特性,在保证估计精度的条件下降低导频数量,从而提高传输效率。文献[8]表明PLC 的信道冲击响应(Channel Impulse Response,CIR)具有稀疏特性,并将正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法应用到PLC 信道估计中,在预先知道信道稀疏度的情况下获得了良好性能;文献[9]基于稀疏度自适应匹配追踪(Sparsity Adaptive Matching Pursuit,SAMP)算法提出一种信道估计算法,在未知信道稀疏度的情况下可获得良好性能。以上方法重点考虑了存在高斯白噪声的情况。对于信道中存在的IN,文献[10]基于稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)算法在单输入单输出(Single-Input Single-Output,SISO)PLC 系统中提出CSI 估计与IN 消除的联合算法,对SISO-PLC 信道进行参数量化,利用信道参数稀疏性进行估计,可有效提高SISO-PLC 系统的抗噪性能。扩展到MIMO-PLC 系统,CSI 与IN 的联合估计同样可以降低IN 对信道估计精度的影响。
为了提升MIMO-PLC 系统的性能,本文利用信道的相关性以及CIR 与IN 的稀疏特性,基于快速块稀疏贝叶斯学习(Fast Marginalized Block Sparse Bayesian Learning,BSBL-FM)算法,对CSI 与IN进行联合估计。该算法将CIR 与IN 时域采样值视为一个联合矩阵,无需预先知道信号的稀疏度,可有效提高MIMO-PLC 系统的抗噪性能,并对CSI 进行精确估计。仿真结果表明,所提方法在插入少量导频的情况下,可以有效保证MIMO-PLC 系统的可靠性,从而提高系统传输效率。
1 系统模型
1.1 MIMO-PLC 信道模型
在家用电缆中存在3 种传输线——相线(P)、中性线(N)和保护地线(PE)。SISO-PLC 系统只使用P-N 来传输信息,而MIMO-PLC 系统可以利用多对传输线(即P-N、P-PE、PE-N)进行数据传输,可有效提高系统容量。根据基尔霍夫定律,只能使用任意两对传输线作为发射端口,实际应用中通常形成2×2 或2×3 MIMO 系统结构[11]。不失一般性,本文主要考虑一种2×2 的MIMO-PLC 信道模型,如图1 所示。

图1 2×2 MIMO-PLC 信道模型
其中,H(mn)(f)表示第m个发射端到第n个接收端的信道频率响应(Channel Frequency Response,CFR)。文献[12]针对SISO-PLC 系统提出一种自上而下的多径信道统计模型,即H(1)(f)可以表示为:
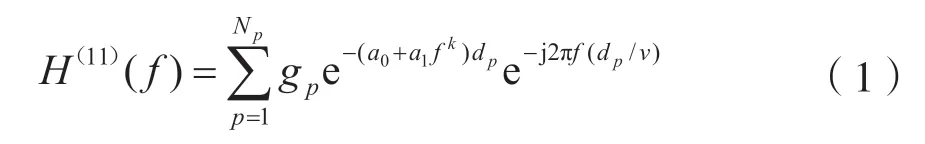
其中Np为路径总数,gp为第p条路径的增益,dp为第p条路径的长度,v为电磁波的传播速度,a0、a1和k为衰减参数。
针对MIMO-PLC 信道,考虑到电力线网络的对称性、子信道呈现的空间相关性[13],MIMO-PLC信道可以分解为多个SISO-PLC 信道的组合,因此每条子信道均可以表示为:
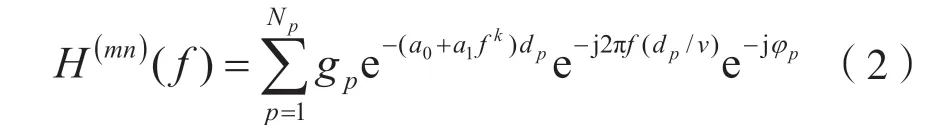
其中,φp为每条路径的随机相位,表示信道空间相关性。
1.2 噪声模型
PLC 中各类噪声与干扰情况十分复杂,总体可以分为两类:背景噪声,包括有色背景噪声、窄带噪声和工频异步周期脉冲噪声;脉冲噪声(IN),包括工频同步周期脉冲噪声和异步脉冲噪声[14]。背景噪声平均功率较小,频谱很宽,类似于白噪声;IN 时变性强且功率大,对信号传输影响更大。本文使用高斯白噪声(Additive White Gaussian Noise,AWGN)描述背景噪声,使用Bernoulli-Gaussian 模型描述IN,即第n个接收端的噪声noise(n)可表示为:

其中,g(n)为均值为0、方差为σg的高斯随机过程,i(n)为伯努利随机过程与高斯随机过程的乘积,即:

其中,P为IN 发生的概率,r(n)为均值为0、方差为σr的高斯随机过程,且与g(n)相互独立,即式(3)可以重新表示为:

因此,它的概率密度可以表示为:
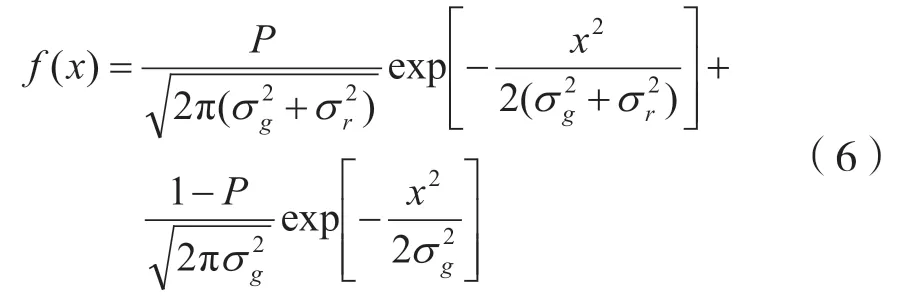
1.3 系统模型
规定MIMO-PLC 系统中第m个发射端口发射 的OFDM频域信号向量为X(m)=[X1,X2,…,XN]T,OFDM 符号的长度为N,则第n个接收端口接收到的该信号Y(mn)可以表示为:
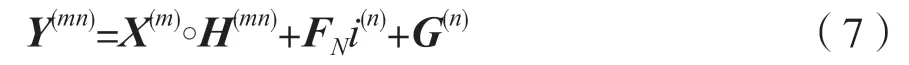
其 中,H(mn)=[H1,H2,…,HN]T为CFR 向 量;FN表示N×N维离散傅里叶变换矩阵;G(n)表示经过离散傅里叶变换的背景噪声,依然为AWGN;○表示哈达玛积。式(7)可以改写为:
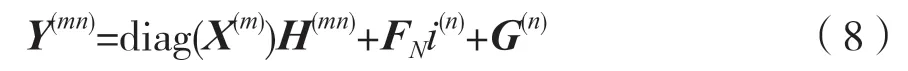
其中,diag(X(m))表示元素为向量X(m)中元素的对角矩阵。
扩展到整个MIMO-PLC 信道,接收信号可表示为:

将式(9)用矩阵表达可简写为:

将式(10)中的CFR 矩阵替换为CIR 矩阵,可表示为:

规定发送信号中插入导频的位置的集合为B,(·)B为集合B中索引对应行或元素构成的子矩阵,式(11)变换为:

2 基于BSBL-FM 的联合估计算法
2.1 问题设置与算法设计思路
PLC 传输信道可建立为多径模型,即信号在PLC 信道上传输时经过多条路径到达接收端。随着信号在电力线上不断反射,信号能量逐渐降低[15]。因此,传输信号的能量主要集中在时延较小的前几条路径上,即PLC 信道的CIR 具有稀疏特性,CIR中不为零的元素个数远远小于元素总数,时域的IN同样具有稀疏特性,所以式(12)可以变换为:
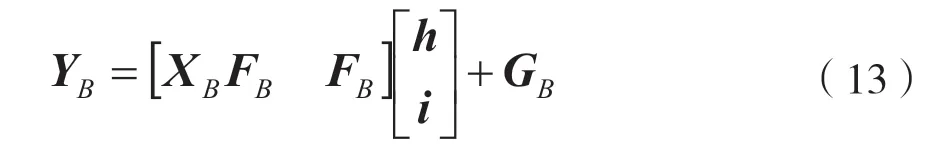
令Φ=[XBFB FB],Z=[hTiT]T,联合估计问题便转换为了典型的CS 问题:

其中,YB为测量矩阵,Φ为观测矩阵,Z为稀疏目标信号,GB为AWGN。
CS 理论利用信号的稀疏性,从信号的有限个映射中可以精确重构原始信号[16]。有多种算法可以解决CS 问题,大致可以分为:凸优化算法,如基追踪算法、梯度投影法等,算法重构精度高,但计算复杂度较高,不适用于实时信道估计问题;贪婪算法,如OMP 算法、SAMP 算法等;贝叶斯估计法,如SBL 算法、块稀疏贝叶斯学习(Block Sparse Bayesian Learning,BSBL)算法等[17-20]。贪婪算法要求观测矩阵满足约束等距特性。本文提出的CS问题中Φ具有强相干性,显然不满足要求。为利用Z的空间相关性,本文采用BSBL-FM 算法进行估计。文献[17]提出BSBL 算法,首次利用信号的分块稀疏性与相关性结构信息,缺点在于计算复杂度较高、重构速度慢。BSBL-FM 算法在不降低恢复精度的条件下,可以加快重构速度,适合用于较大维度信号[21-22]。综合上述分析,结合本文MIMOPLC 信道CSI 与IN 的联合估计问题,提出一种基于BSBL-FM 的联合估计算法。
2.2 基于BSBL-FM 的联合估计算法
MIMO-PLC 系统中基于BSBL-FM 的CSI 与IN联合估计算法具体实现步骤如下[23-25]。


通过上述BSBL-FM 联合估计算法,可精确估计信道的CIR 与IN。得到IN 估计值后,噪声抑制过程可以表示为:

经过IN 抑制后,残留的IN 可以视为背景噪声。
上述讨论了2×2 MIMO-PLC 系统中的联合估计算法流程,通过更改式(9)中的矩阵维度,即可将该算法扩展到其他MIMO-PLC 系统中。
3 仿真结果与分析
本文将所提的基于BSBL-FM 的联合估计算法在MIMO-PLC 系统模型中进行仿真,信道参数如表1 所示。

表1 MIMO-PLC 信道参数
系统中OFDM 采用正交相移键控(Quadrature Phase Shift Keying,QPSK)调制,子载波数为N=512,插入循环前缀长度为128,导频均匀放置。
本文用均方误差(Mean Square Error,MSE)和误比特率(Bit Error Rate,BER)衡量信道估计算法的性能,将所提的基于BSBL-FM 的联合估计算法与以下4 种方法进行对比。
LS 估计:用最小二乘(Least Square,LS)算法进行信道估计;
LS-Bl 估计:用消隐法对IN 进行抑制,再进行LS 信道估计;
MMSE 估计:用最小均方误差(Minimum Mean Squared Error,MMSE)算法进行信道估计;
MMSE-Bl 估计:用消隐法对IN 进行抑制,再进行MMSE 信道估计。
图2 对比了导频数量为128 时不同方法的MSE性能。可以看出,SNR较低时,IN 对信道估计的性能影响较大。当SNR<10 dB 时,未经过IN 抑制的LS 估计与MMSE 估计的MSE很高,不能精确获取信道的CSI;在接收机处用消隐法抑制IN后,性能有所提升,但仍比所提的BSBL-FM 联合估计算法差。当SNR>10 dB 时,是否用消隐法抑制IN 对LS 估计与MMSE 估计的性能影响较小,BSBL-FM 联合估计算法性能更好。所以,BSBL-FM联合估计算法无需提前进行IN 消除,简化了接收机的结构,并且在任何SNR条件下均表现出更高的估计精度。
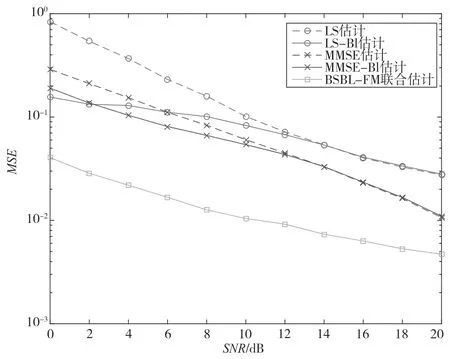
图2 导频数量为128 时各算法的MSE 性能比较
图3 对比了导频数目为128 时抑制IN 后不同方法的误比特率性能。随着SNR 的升高,BSBL-FM联合估计算法的BER 越来越低,且一直优于其他两种算法,表明BSBL-FM 联合估计算法可显著提高MIMO-PLC 系统的可靠性。
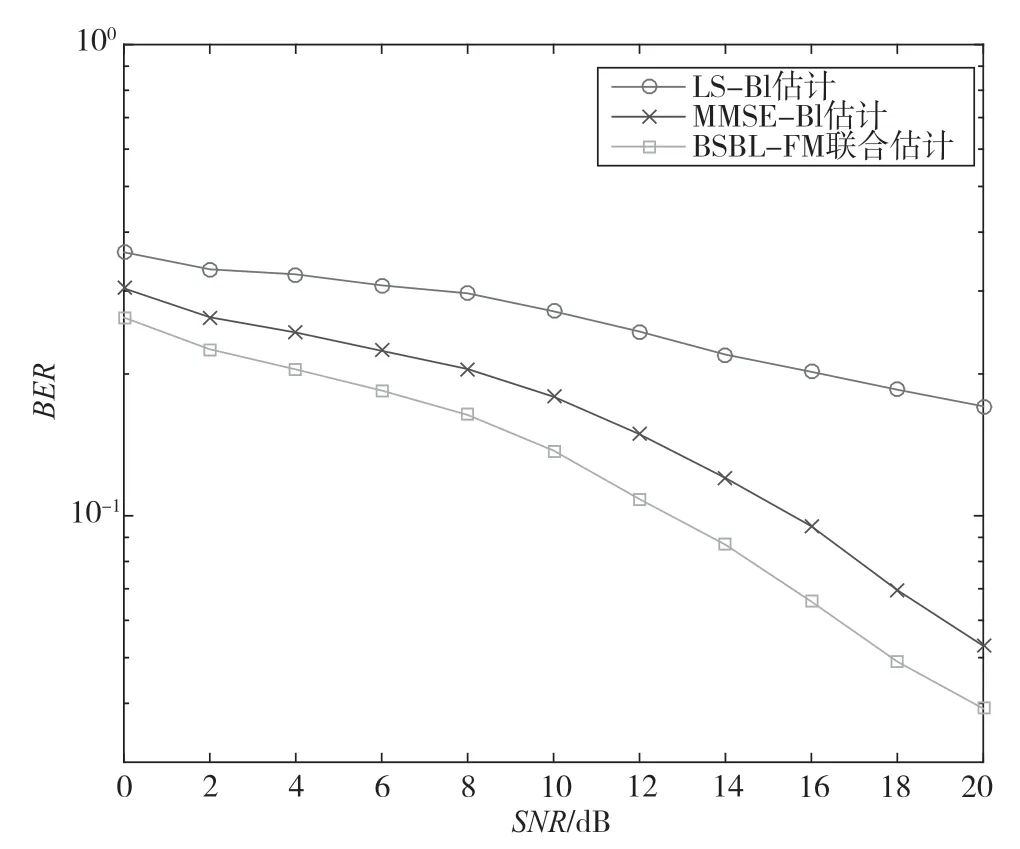
图3 导频数量为128 时各算法的BER 性能比较
图4 对比了导频数目为128 与64 时,不同方法的MSE 性能。可以看出,随着导频数目增加,3种方法的MSE 均逐渐降低,且BSBL-FM 联合估计算法的性能始终优于其他两种算法。导频数目为64的BSBL-FM 联合估计算法的性能明显优于导频数目为128 的“LS-Bl”估计的性能,在SNR<18 dB时优于“MMSE-Bl”估计的性能。由此可见,BSBL-FM 联合估计算法插入更少的导频就可以达到更高的估计精度,在低信噪比条件下性能提升更显著,可以有效提高MIMO-PLC 系统的传输效率和可靠性。
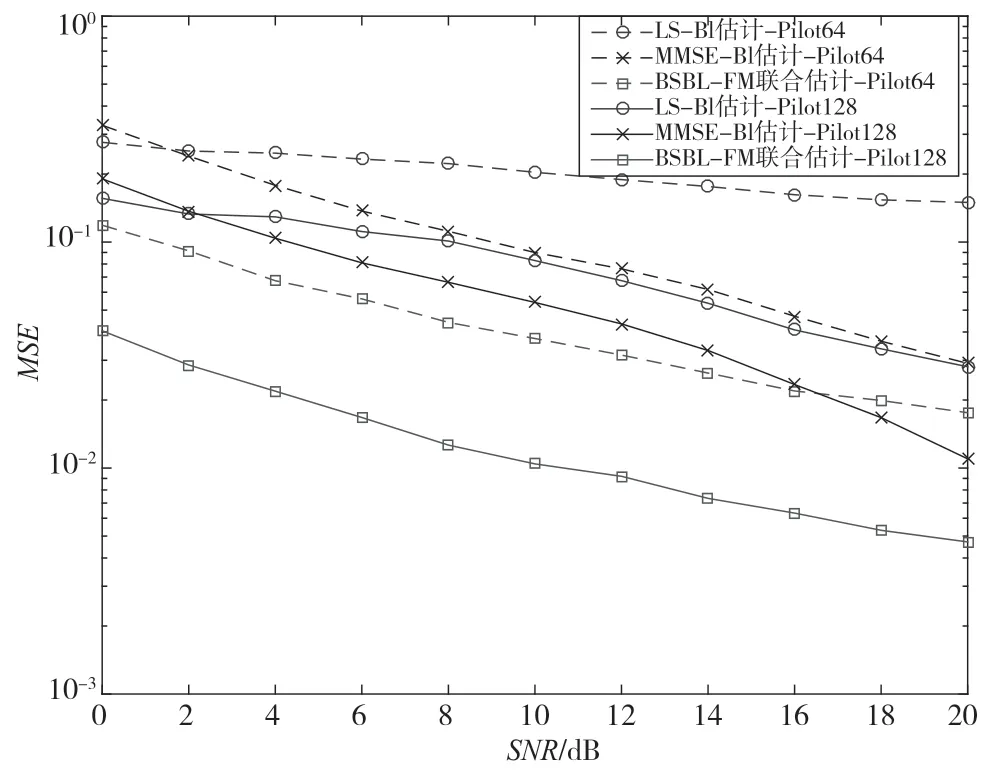
图4 不同导频数量下各算法的MSE 性能比较
4 结语
本文基于CS 理论,利用MIMO-PLC 信道的相关性以及CIR 与IN 的稀疏特性,提出了一种基于BSBL-FM 的联合估计方法。与传统信道估计和IN抑制方法相比,所提方法所需导频数目更少且具有更好的抗噪性能,可以有效提高MIMO-PLC 系统的传输效率与可靠性。
