轻型堤块系统概念重建与优化

侯武杰，刁景华，同建辉

(1.海军勤务学院，天津 300450；2.阳光大地(天津)环保工程有限公司，天津 300393)

所谓堤道系统，就是通过快速部署到军事形势较为严峻或受灾地区，将人员和物资运送上岸的一种桥接系统[1]。

1 堤道系统发展概况

第二次世界大战期间，诺曼底登陆时开设的“桑树”人工港首次使用了堤道系统。随后分别研制了能够适应2级海况的海军驳船系统[2]、模块化堤道系统[3]和联合模块化驳船系统[4-5]以及能够适应3级海况的高架堤道系统[4-5]。其中海军驳船系统由长宽分别为27.43 m和6.40 m的钢模块组成，但该设计并不符合国际标准，需要特殊的起重设备进行安放；模块化堤道系统的设计符合国际标准，可以采用浮动堤道、滚动或滚降安放设施、驳运门桥、绞滩拖船等多种不同的方式灵活配置；联合模块化驳船系统由长宽高分别为12.19 m、2.44 m和2.44 m的钢模块连接而成，连接和配置方式都很灵活，但存在模块间出现裂纹、侧向连接系统不稳定等风险和不足；高架堤道系统由模块化部件焊接而成，通过转盘实现了物资的双向传输，是目前最有效的海岸间物资运输的堤道系统。

上述堤道系统在特定的历史环境下都发挥了一定的作用，随着时代的发展，堤道系统需要战略性海运资源(大型运输船等)运输和部署的矛盾也逐渐凸显，为此设计了轻型堤块系统。该系统由长3.05 m、宽6.10 m的12个模块单元组成，上部为铝制结构，下部为气动浮筒，模块之间采用端到端进行连接[6]，便捷高效。

该系统的设计主要考虑了四个方面的因素：一是确保吃水较浅的船只能够在恶劣环境(如泥滩或湿地)或港口损坏(浅水或软土条件)的情况下迅速展开堤道部署；二是设计符合国际标准配置，可综合运用陆运、海运、空运等多种方式实施战略投送；三是便于组装；四是模块单元重量轻，体积小。其最大优势在于可以使用联合高速船、后勤支援舰或军用驳船运输，通过浮筒充气、模块连接等方式，使堤道系统快速部署到水深较浅的前沿军事地域，并且能够支撑多辆主战坦克同时通过。

2 轻型堤块系统概念重建的思路

轻型堤块系统在现场实验和评估中显示出了良好的前景和性能，但连接设计比较复杂，连接部件重量占到每个模块自身重量的一半，需要重新定义现有的设计，选择现有铰链的旋转柔度，充分利用下部浮筒的浮力实现旋转。

图1为轻型堤块系统的三种不同配置形式，曲线表示水位。若系统是刚性的，即模块之间进行完全力矩连接，那么该结构就不能充分利用波浪间的浮力(如图1-a所示)。若能采用柔性连接(如图1-b所示)，就可以更好地利用波浪间的浮力(如图1-c所示)。

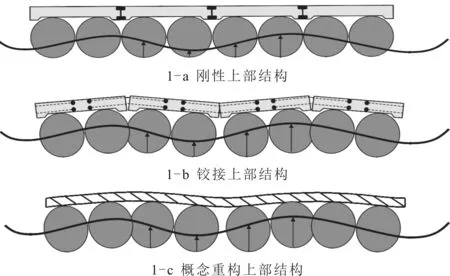
图1 堤道系统配置Fig.1 Configurations for causeway system

图2-a为轻型堤块系统内部的具体连接方式，这种连接方式既繁重又复杂。概念重建的目的就是通过将旋转柔度传递到甲板自身来消除刚性连接，在给定载荷条件下，可通过将甲板刚度降低到目标值来实现特定的旋转。设计目标是在1 140 kN·m荷载条件下，使甲板在3.05 m长的模块上旋转0.08 rad(堤道支撑一个坦克和斜坡负载时的设计弯矩)。图2-b则是一种更轻型、更简单的模块连接方式，且模块可以分开进行运输。此外，模块采用重量轻、耐腐蚀的玻璃纤维增强聚合材料设计，并将其横截面改为箱梁结构。

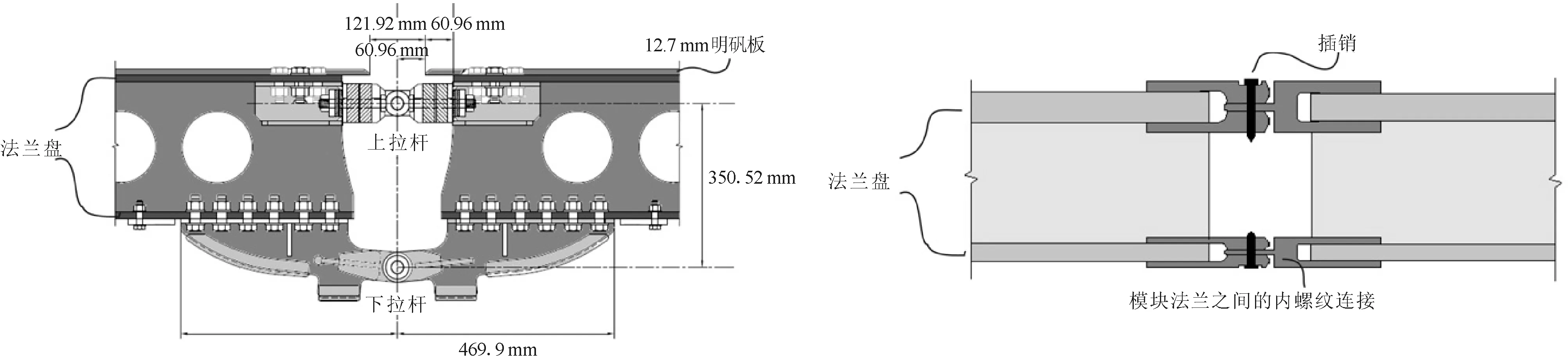
2-a 轻型堤块系统原设计的连接方式 2-b 用于概念重构系统的力矩连接图2 铰链配置Fig.2 Hinge configurations

3 轻型堤块系统的设计优化

堤道系统的自身重量和体积对于可部署结构设计来讲非常重要。对于概念重建的轻型堤块系统而言，在符合美国钢结构规范中关于拉挤玻璃钢结构条件和几何要求前提下，运用多目标结构优化算法，以最小目标刚度值为约束条件，求得系统的最小自重和刚度。目前，多目标结构优化算法被广泛应用于浮动甲板设计、永久桥面铺装系统设计以及桥梁修复工程中，其中遗传算法是应用最广泛的一种优化算法，其不仅能避免局部最小值，还可以处理离散和不可微分优化函数。

3.1 问题分析

概念重建就是探索一种具有目标刚度的轻量化设计方法。即在符合钢结构规范和封装标准的基础上，以惯性矩不低于目标值为约束条件，对最小自重和最小惯性矩进行多目标结构优化。

其中，设计变量与箱梁截面有关，包括整个截面深度H、上下翼缘厚度tft和tfb、下翼缘宽度wfb、外腹板厚度twe(图3)。

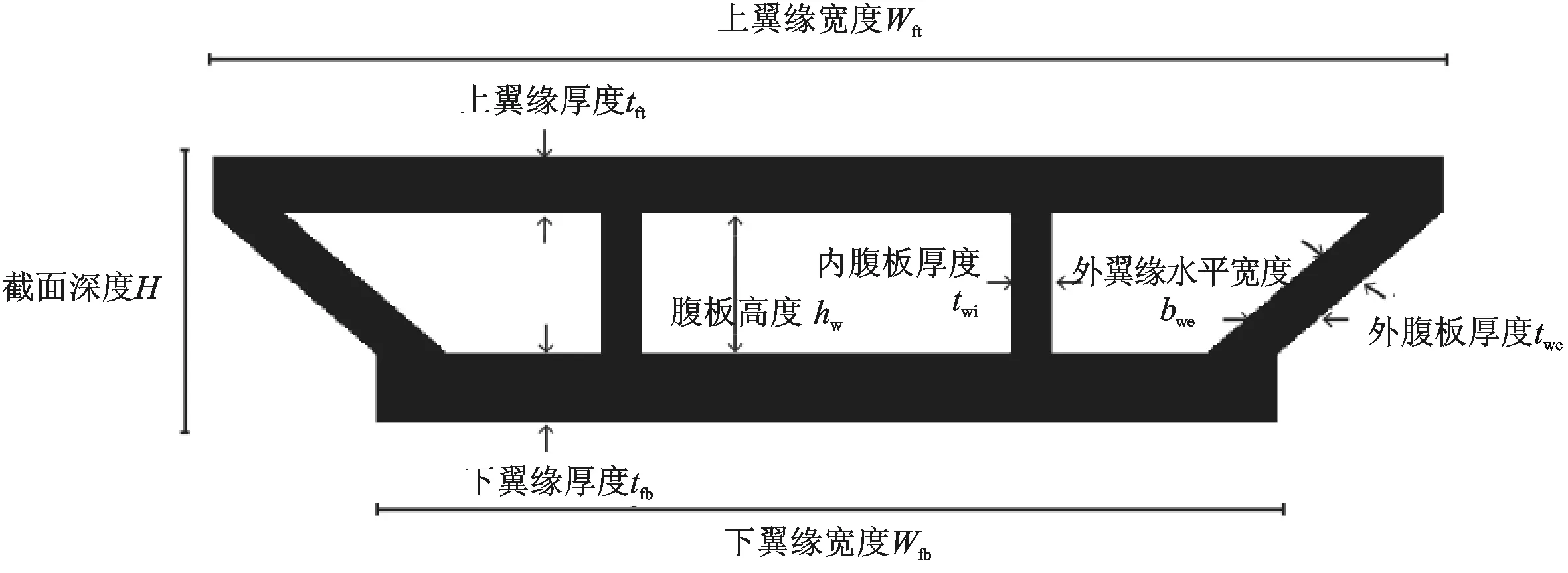
图3 一般的横截面Fig.3 General cross section

这些变量从9.5 mm开始以3.2 mm的增量不断增加到6 096 mm。图3中wft为上翼缘宽度、hw为腹板高度、bwe为外翼缘水平宽度，按照设计要求，上翼缘宽度wft=6 096 mm为固定值，内部腹板的数量n和厚度twi在算法中确定。最后两个维度与设计变量的几何关系如下

hw=H-tft-tfb

(1)

(2)

这是简化后的方程。该优化问题的正式定义如下

使得

(3)

式中：W为上部结构的自重，即每个元素的面积乘以密度p的总和。转动惯量目标函数Ix由平行轴定理得到，其中d为单个构件质心到整个上部构件质心的距离。最后，算法生成的截面必须符合u个约束条件，其中c1代表最小转动惯量值，c2～c6为钢结构规范手册的约束条件，几何约束条件c7、c8为封装标准。表1列出了军事桥接系统的负载组合作用于系统的设计弯矩、剪力和扭矩的具体数值，并将其分别乘以荷载系数1.33以满足钢结构规范设计。

表1 设计弯矩、剪力和扭转Tab.1 Design moment, shear and torsion

第一个约束条件c1通过设置一个较低的限制，以确保上部结构的惯性矩不超出预期的灵活性。即

(4)

式中：p为所需的曲率半径；MS为工作荷载作用下的弯矩(如表1所示)；EL为纵向弹性模量。在运用弯矩与曲率关系时，假定截面为平面，材料为有限弹性材料。均匀弯矩下，在3.05 m长的模块上期望旋转0.08 rad，目标惯性矩为0.003 503 m4。

钢结构规范手册中定义的结构性限制标准，与材料切变(材料在剪切破坏、腹板剪切失稳和腹板横向稳定性等因素作用下而引起的构件强度)、弯曲(材料断裂和局部不稳定性导致的构件强度)、扭矩(强度控制下的扭转能力)和集中负荷需求(腹板拉伸断裂、腹板破坏、腹板压缩屈曲和翼缘弯曲破坏而引起的构件强度)等因素有关。在所有的计算中，假定玻璃纤维增强聚合材料构件具有相同的性能，且不发生分层或分离。

第二个约束条件是基于材料剪切破坏与腹板剪切屈曲之间的控制行为。剪切能力Vn必须超过剪力需求Vu，关系如下所示

c2=Vu-λφVn≤0

(5)

式中：λ=0.8为时间效应因子；φ为剪切阻力系数，系统的剪力需求为表1给出的值乘以荷载系数1.33。对于剪切过程中的材料断裂，φ=0.65，Vn=FLTAs，其中FLT为平面抗剪强度特性、As为剪切面积(As=Hbwe)。此处的剪切面积指的是单腹板的面积，实际上剪力会通过几个或全部腹板传递到截面上，由于每个腹板所承载的剪力需求只能通过详细的有限元分析得出，为了计算方便，假设任何单个腹板必须能够承载全部的剪力需求，最终设计时，通过详细分析每块腹板的实际需求来减少腹板的宽度。对于腹板剪切屈曲，φ=0.80，Vn=FcrAs，其中Fcr为临界剪切屈曲应力，为设计变量twe和H的函数。

第三、四个约束条件用来检查该部分是否满足弯曲要求。约束条件c3是确保材料在弯曲过程中不会断裂。弯曲能力Mn必须超过需求Mu，关系如下所示

c3=Mu-λφMn≤0

(6)

式中：阻力系数φ=0.65，弯曲能力的计算公式为Mn=FLIx/y，其中FL为纵向抗弯强度，y为截面中性轴到构件极端纤维的距离。Mu为因式矩(1.33乘以表1设计值)。

第二个弯曲约束是用来检查外部腹板是否足够厚，防止局部不稳定。即

c4=twer-twe≤0

(7)

twer为所需的腹板厚度，通过如下公式求得

(8)

式中：φ=0.65；EL,w和ET,w分别表示腹板的纵向弹性模量和横向弹性模量；vLT为纵向泊松比；GLT为平面剪切模量。

第五个约束条件c5与构件的扭转能力有关，定义为

c5=Tu-λφTn≤0

(9)

式中：Tu为所需扭转量(1.33乘以表1设计值)；φ=0.70；Tn为抗扭承载能力。封闭截面的抗扭承载力为Tn=2tFLTAo，其中t为任意外部单元的最小厚度，Ao为外部单元中心线围成的面积。对于集中负荷，负荷需求Ru必须超过容量Rn，如下所示

c6=Ru-λφRn≤0

(10)

系统的负荷需求主要是坦克的集中载荷以及船与堤道相连的坡道重量，坦克的集中载荷可以看成是其重量除以车轮的数量(Ru=68 kN，包括负载系数)。该约束条件主要考虑了腹板拉伸断裂、腹板破坏和腹板压缩屈曲等三种极限状态的情况，分别对内外腹板进行了详细分析，并使得φRn最小。对于腹板拉伸断裂的情况，Rn=ltenFT,wtw，其中lten为腹板高度，FT,w为腹板的横向抗弯强度，同样假设需要一个腹板来承载全部负载，因此tw的值为内外腹板中最薄腹板的厚度(twe或twi)，在这种极限状态下φ=0.65。对于腹板破坏严重的情况，φ=0.70，Rn=0.7hwtwFsh,int{1+[(2k+6tplate+bplate)/dw]}，式中Fsh,int为层间剪切强度，k为构件顶部到圆角底部的距离，由于截面上没有圆角，所以取上翼缘的厚度tft代替，tplate和bplate分别为承重板的厚度和长度，由于不存在承重板，取上翼缘的厚度和宽度代替，最大值为102 mm，dw为腹板深度，在本案例中就是腹板高度hw。对于腹板压缩屈曲的情况，φ=0.80，Rn=fcrAeff，其中Aeff为有效面积(Aeff=lefftw，其中leff为腹板深度dw或上下翼缘之间垂直距离的较小者)，则fcr为

(11)

第七个、第八个约束条件是与功能需求、包装需求和物理约束相关的几何约束。上、下翼缘之间的夹角必须大于45%，可正式表示为

c7=wft-wfb-2H≤0

(12)

对于包装需求来说，横截面的深度必须足够浅，使得4个模块可以安装在一个标准容器中(最大深度为400 mm)。

c8=H-400 mm≤0

(13)

第九个、第十个几何约束是确保模块的横截面如实存在，具体来说，上、下翼缘的厚度不能大于整个构件的高度。

c9=tft+tfb-H≤0

(14)

并且外部腹板的厚度不能大于横截面的宽度。

c10=2twe-wft≤0

(15)

内部腹板的数量和厚度没有设置为变量，而是通过计算以满足各种极限状态。受压翼缘构件的强度是由整个截面弯曲所引起的局部不稳定性和翼缘抗压弯曲破坏造成的，而内腹板的数量正是按照保持受压翼缘构件稳定的标准设计的，由于截面的上翼缘和下翼缘都能受压，因此有必要对它们分别进行分析，并提出基于集中荷载要求nwi的计算方法

(16)

式中：FT，f为翼缘横向抗弯强度，φ=0.65，nwi为这两个计算之间的控制值。假设内部腹板在整个截面上均匀间隔，并且集中力作用在最关键的位置，即两个腹板之间的中间位置，腹板厚度是由材料在剪切破坏、腹板剪切失稳和弯曲局部失稳之间的控制计算确定的，与外部腹板计算的情况一样，仍然假设任何单个腹板必须能够承载全部的剪力需求，材料剪切破坏与腹板剪切屈曲仍然由c2中描述的相同方程导出，重新排列后得到twi(代替了c2方程中的bwe和twe)，根据弯曲不稳定性检验，所要求的腹板厚度与c4中描述的相同。

如前所述，对A709 HPS 70钢(屈曲强度为483 MPa)和A709 HPS 100钢(屈曲强度为689 MPa)两种高强度钢进行了类似的处理。设计变量和目标函数保持不变，但是结构约束c2～c6由美国公路桥梁设计规范中的约束代替，用于钢箱梁的设计。目标转动惯量c1也进行了改变，以获得相同的刚度和不同的弹性模量0.000 217 m4。

3.2 模拟退火算法

模拟退火算法是一种基于晶体形成类比的迭代改进算法，在物理降温过程中，随着熔化体的缓慢冷却，系统的能量逐渐降低，在此过程中存在可能发生更高能量配置的概率P，这最终会导致更低的能量配置。概率公式P=e(-ΔE)/T，其中ΔE为能量构型差，T为物体温度，当温度降低时，发生高能量状态的可能性就会降低。这一过程可以扩展到结构优化，其中概率与接受高值函数的概率有关，能量与现有函数有关，T为用户可以控制的变量，从而使算法能够摆脱局部最小值。

对于单目标模拟退火算法(如最小权值优化)，该算法首先从用户指定的离散值数据库中随机生成一组可行的设计变量，选择初始解。这个集合成为初始的最佳解。然后随机扰动一个或多个变量，生成一个新的解，如果该解符合所有约束条件，并能得到一个较低权值的解，它就成为新的通用解，当然也存在一定概率没有最佳解，但它仍然可以作为当前的解决方案接受，算法在此基础上继续迭代。

这种对单个设计变量进行优化的过程可以推广到多目标优化，不是使用加权平均将目标函数组合在一起，而是将目标函数分离以产生帕累托最优解集，如果在任何一个目标函数中，该解都不被其他解所掩盖，那么该解就是帕累托最优解。在收敛过程中，帕累托最优解集为设计者提供了一系列可能的解，这些解跨越了通过单目标优化可以找到的两个极端，根据设计优先级，设计师可以选择最终的解决方案。

3.3 优化设计

从本质上讲，启发式算法并不能保证每次使用时都收敛于同一个解。用户定义了几个参数，包括v(一次变量变化的最大数量)、pm(允许值数据库允许的扰动量)、r(降温因子)、m(冷却周期的长度)和n(算法收敛的冷却循环次数)。算法的质量和鲁棒性取决于这些参数的选择(鲁棒性是指同时具有较低的平均值和标准差)。为了确定这些参数对多目标优化的鲁棒性选择，对每个目标函数使用16种不同的参数组合v、pm、r、m和n进行单目标优化，对每种组合进行20次数值模拟。表2给出了考虑的组合以及玻璃纤维增强聚合材料设计的平均结果μ、标准差σ和变异系数cv。对于两个目标函数，最稳健的组合是SA4(v=1；pm=10；r=0.8；m=10 000；n=2；在表2中以粗体突出显示)。

表2 玻璃纤维增强聚合材料设计的模拟退火数值实验Tab.2 Simulated annealing numerical tests for GFRP design

通过这些参数的选择，对玻璃纤维增强聚合材料进行多目标模拟退火算法设计，找到了帕累托最优结果集，设计者可以从中选择最终的设计(如图4中空心圆所示)。菱形和方形分别代表了重量和惯性矩的单目标优化的最佳结果，代表了帕累托最优集跨越的两个极值，虚线表示目标转动惯量值，转动惯量和重量的最佳组合由一个填充圆所表示的横截面来表示。该方案的惯性矩接近目标值(0.003 504 m4)，重量也可以接受(包括浮体重量在内，为1 208 kg/m)，对应的截面如图5-a所示。对这两种等级的钢进行了类似的处理，得到的优化截面如图5-b和5-c所示。

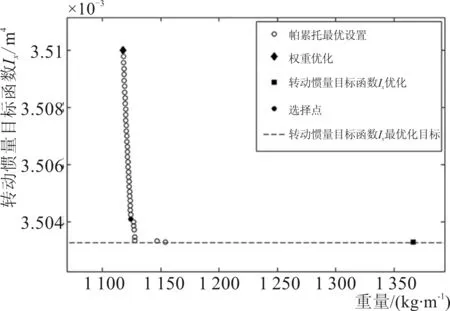
图4 多目标模拟退火算法数值模拟得出的帕累托最优解集Fig.4 Pareto-optimal (PO) set of solutions from one multiobjective simulated annealing (MOSA) numerical simulation

5-a 优化的玻璃纤维增强聚合材料截面

表3对优化结果进行了总结，并与现有的轻型堤块系统进行了比较，所采用的三种优化设计均达到或接近所需的系统目标刚度，因此可以根据需要设计铰链的连接方式，可采用图2-b所示的简化连接替换。除了简化连接之外，最重要的任务之一就是减少系统的总重量，表3给出了单独的模块重量W(不含铰链和浮漂)、有连接的模块重量(含铰链，不含浮漂)以及包含浮漂的系统总重量。但由于顶部翼缘的局部约束，玻璃纤维增强聚合材料的设计并不能使系统的重量降低，而两种钢的设计都比玻璃纤维增强聚合材料设计的方案重量轻，其中A709 HPS 100钢的设计方案使得堤块系统重量较现有系统重量轻。此外，系统的上部结构高度H被降低，使得一个标准容器可以装运更多的模块，减少了运输时间和包装成本。

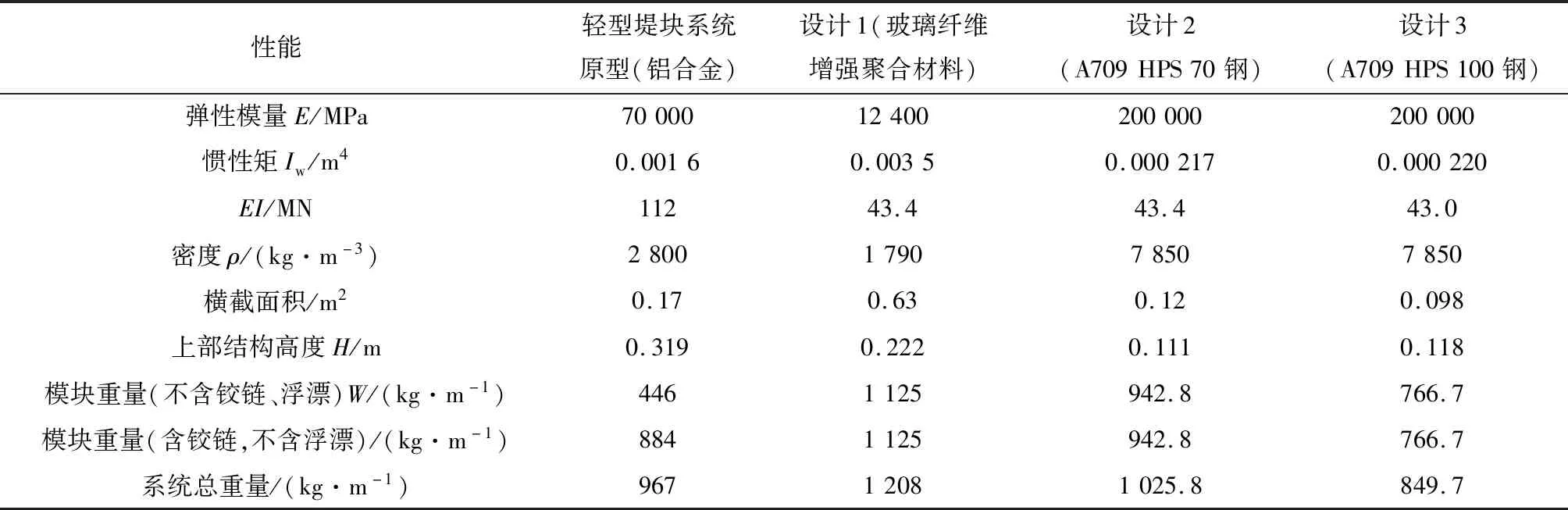
表3 轻型堤块系统原型与设计方案的比较Tab.3 Comparison between original prototype and proposed designs

4 结论和展望

本文研究提出了一种基于玻璃纤维增强聚合材料和两种高强度钢的多目标结构优化的轻型堤块系统，所得到的设计结果均达到或接近系统所需的目标刚度，以取代繁重复杂的连接，并建议简化连接。这比原系统的兼容连接更简单、更轻便、更容易部署和维护，也使得系统上部结构设计制造和部署更为简单。每一个优化设计降低了截面深度，从而减少了运输成本和时间。虽然玻璃纤维增强聚合材料和A709 HPS 70钢的设计并不能降低整个系统的重量，但是A709 HPS 100钢的设计达到了降低系统自重的目标，从而实现了该项目的设计优先级。

在对重新定义的轻型堤块系统进行初步优化设计的基础上，下一步需要继续深入研究详细的连接设计，分析通过减小腹板宽度来减轻系统自重的可能性，并要考虑材料和制造成本，以及横截面的可构造性和部件之间的连接细节等。