浅析物理模型在解题中的应用

刘相周

一、会“命题”

会“命题”，是指会对物理模型的条件进行变化而得到考查点不同的题。命题能帮助学生理解题中考查的知识点，帮助学生学会带着问题去读题。例如：力学、运动学和牛顿运动定律等知识点看似彼此孤立，内容却紧密相连。学完这些知识后，我们可以通过建立一个“水平面上物体运动”的模型，将所学知识串联起来。这个物理模型涉及的物理量可能有：物体的质量、物体的受力、物体的初速度、物体的末速度、物体的加速度、物体运动的时间等；涉及的物理知识点可能有：力学知识（包括重力、弹力、摩擦力、力的合成与分解等）、运动学知识（包括匀变速直线运动的速度与时间关系、匀变速直线运动的位移与时间关系、匀变速直线运动的速度与位移关系等）等。我们建立这样一个物理模型后，只要附加几个条件就可以得到一个新的题目。

例1：在光滑的水平面上一质量m=2kg的物体，在水平拉力F=6N的作用下，由静止开始从A点经过t=5s运动到B点，求物体运动到B点速度的大小。

倘若在此模型的基础上改变条件，比如将“光滑水平面”改为“粗糙水平面”，那么题中可以考查“滑动摩擦力”等知识点。如果再继续改变条件，如将“物体由静止开始运动”改为“已知物体的末速度”，将问题“物体运动到B点速度的大小”改为“物体在A点的速度大小”，那么题中还可以考查“运动学公式的数学变化”等知识点。

物理模型中变化的条件越多，题目考查的知识点就越丰富，难度也会相对提高。学会了运用物理模型进行命题，就是学会了带着知识点去思考题意，能达到事半功倍的审题效果。

二、会“拆题”

会“拆题”，是指在处理多过程综合性问题时，我们要学会将综合性大过程拆解成一个个独立的小过程，然后通过建立的物理模型对每一个小过程进行分析解决。

例2：在动摩擦因数μ=0.2的粗糙水平面上，一质量m=2kg的物体，在水平拉力F的作用下由靜止开始运动，经过t=5s到达B点，后进入半径R=5m的半圆形光滑轨道并恰好能到达C点（C为半圆形轨道的中点）。问：水平拉力F应该为多大？（取g=10？m/s2）

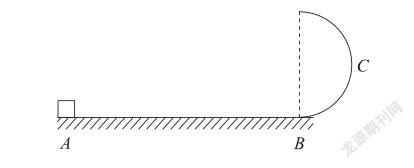
题中物体的运动过程是一个综合性大过程，解决此题时我们可以将题中的综合性大过程分解成两个独立的小过程：水平面上的直线运动和竖直面上的圆周运动。第一个小过程我们可以建立“水平面上的直线运动”的物理模型，利用力学、运动学和牛顿运动定律的知识点进行解决；第二个小过程我们可以建立“竖直面上的圆周运动”的物理模型，利用“竖直面上的圆周运动”物理模型中动能定理的知识点进行解决。其中B点是两个过程的连接点，既是第一个过程的终点，也是第二个过程的起点，所以分析好B点并得到物体在B点的速度是我们解决此题的关键。

在处理综合性问题时，若能充分把握好“拆”字，可以将复杂的问题简单化，物理模型的应用也会得心应手。

三、会“融题”

会“融题”，是指能将我们学过的数学、物理等知识，通过物理模型巧妙地融合在一起。如果我们将学到的知识“融会”成一个有机的整体，并达到“贯通”的目的，那么无论多么复杂的物理情境，用物理模型处理起来都会显得游刃有余。

例3：在动摩擦因数μ=0.2的粗糙水平面上，一质量m=2kg的物体，在水平拉力F的作用下，由静止开始运动，经过t=5s到达B点，后进入半径R=5m的半圆形光滑轨道。求物体不脱离轨道时水平拉力F的范围。（取g=10？m/s2）

要解决此拉力F的范围应该是解不等式，但如果将物理模型融入此题目中并通过分析找到物体不脱离轨道的两个临界条件，那么看似复杂的不等式问题就变成了简单的临界问题，最后经过归纳综述就可以将问题解决。

此题中物体不脱离轨道的条件有两个：一个是物体恰好到C点，另一个是物体刚好能够过D点。在例2中，我们已经对物体恰好到C点进行了详细的分析，这里我们可以用同样的方法分析D点，只是要用到在“竖直面上的圆周运动”的物理模型中找到恰好过最高点D的条件（即F向=G）。我们利用这个条件就可以得到物体在D点的速度，然后利用“竖直面上的圆周运动”的物理模型中动能定理的知识点求出物体在B点的速度，最后就能解答此题。

由此可见，物理模型的运用不是单纯的物理知识的运用，还包括数学等相关学科知识的综合运用。

高中物理学习是一个由易入难、循序渐进的过程，通过运用物理模型，我们可以将复杂问题简单化，零散知识系统化，解题思路清晰化，让物理学习由“难”变“易”。

（作者单位：莒县第一中学）