交流异步电动机矢量控制系统的建模与仿真
2020-09-26林海翔

摘要:交流异步电动机作为重要的调速传动设备,具有结构简单、造价低、可靠性高、便于维护等诸多优点,但相对于直流电动机,其调速性能还有待提高。现介绍了交流异步电动机矢量控制的数学模型,阐述了系统仿真模型的建立过程,最后运用SIMULINK软件对转差型矢量控制变频调速系统进行了仿真分析,根据仿真分析结果可知,交流异步电动机采用矢量控制系统后,其动态和静态性能均有了较大提高。
关键词:交流异步电动机;矢量控制系统;SIMULINK仿真
1 交流调速技术
自20世纪70年代以来,随着电力电子技术、控制理论及电机学理论的发展,交流调速系统在调速性、能效性等方面取得了较大突破,先后出现了一批具有代表性的高性能调速技术,如矢量控制技术、直接转矩控制技术等。
1.1 矢量控制技术
德国西门子公司的Felix Blaschke博士首先提出了磁场定向矢量控制理论,他指出矢量控制(VC)是模拟直流电动机的控制方式,利用坐标变换得到解耦后交流电动机三相定子电流的两个分量:转矩分量和励磁分量,然后对它们分别进行调节,让交流电动机变成直流电动机,进而得到较好的转矩输出特性及转速响应特性。目前,电动机矢量控制方式主要有转差频率矢量控制和磁场定向矢量控制两种。实践证明,通过模拟直流电动机的控制方式来控制交流电动机,大大提高了调速系统的动态响应特性。
1.2 直接轉矩控制技术
20世纪80年代,德国学者彭布罗克在实际应用直接转矩控制(DTC)技术时获得了成功。他提出了利用空间矢量分析法构建电动机的转矩模型及磁链模型,以控制电动机输出转矩,进而实现对电动机的直接转矩控制。定子磁链可以通过定子电阻测出,避免因参数变化带来的影响,其结果精确可靠,所以异步电动机直接转矩控制技术计算容易、结构简单、动态响应性能较好,但该调速系统在低速运行时还存在一些问题需要解决,如死区效应、转矩脉动等。
实践表明,矢量控制和直接转矩控制技术都实现了高性能的电动机调速控制,这两种调速方式都能获得较好的静、动态响应特性,普遍适用于各种高性能调速领域。但因为这两种控制方式不同,它们的特点也不同,应用领域各有侧重。采用砰-砰控制的直接转矩控制技术的转矩响应快,参数鲁棒性好,还可以获得较高的瞬时转矩,发展前景非常好。相比之下,矢量控制技术在连续控制、低速控制、调速范围等方面优势明显。在一些对系统动态性能要求不高而更加看重变频器效率、容量利用率的应用场合,例如在水泵的节能传动、风机的节能传动等一般的工业机械传动场合,矢量控制技术得到了广泛应用。因此,作为一种重要的交流调速技术,矢量控制技术值得进一步做深入研究。
2 交流异步电动机矢量控制的数学模型
2.1 运动方程与转矩方程
对于恒转矩负载,其运动方程为:
式中:J为转动惯量;np为电动机极对数;TL为负载转矩;Te为电磁转矩;ω为角速度。
式中:np为电动机极对数;θ为空间电角度;i为定子电流。
2.2 交流异步电动机数学模型
汇总交流异步电动机定/转子电压方程、运动方程、磁链方程及转矩方程,根据微分方程可得出交流异步电动机的数学模型:
3 系统仿真模型的建立
当转子短接时,可以得到二相同步旋转坐标系上按转子磁场定向的三相异步电动机矢量控制方程:
笔者发现在矢量控制中,定子电流被分解为iM1和iT1两个相互垂直的分量,其中iM1调节转子磁链,为磁链分量;iT1用于控制电动机输出转矩,为转矩分量。由此可见,矢量控制通过坐标变换实现了定子电流分解,最终可以模拟直流电动机分别进行转矩和磁通的解耦控制。
3.1 转差型矢量控制的变频调速系统
转差型矢量控制的基本方程:
式中:np为电动机极对数;ωs为转差频率;ψ2为转子总磁链。
3.2 异步电动机矢量控制系统仿真模型的建立
该模型是在转差型矢量控制变频调速系统基础上构建的,系统由控制模块、给定模块、运算转换模块及逆变器组成。Speed controller模块是速度控制模块,以它的输出作为转矩给定信号T * e。I * t Calculation模块是电流控制模块,它是通过转子磁通量Phir和给定转矩信号T * e来计算定子电流转矩分量值I * t,该值为给定值。DQ-ABC模块是坐标变换模块,它能够实现DQ两相到ABC三相坐标系的转换,将DQ坐标系中定子电流在分量经过旋转变换后,得到定子三相绕组的电流给定值Iabc。Current Regulator是电流调节模块,它是采用电流滞环控制原理进行调节,使实际输出电流的变化跟随给定值变化。Teta Calculation模块为计算角度模块,它可以计算出旋转磁场与旋转坐标的空间电角度θ,即M轴的位置。ABC-DQ模块是坐标变换模块,它的作用是根据电角度θ将电机实际三相定子电流Iabc变换得到其在DQ坐标系下的两个分量Id和Iq。Flux Calculation模块为计算磁通模块,它能够根据定子电流励磁分量Id来计算出电机转子的磁通Phir。
转差型异步电动机矢量控制系统仿真模型如图2所示。
3.3 主要的子模块功能
3.3.1 Iq* Calculation子模块
该子模块用于计算电动机定子绕组电流在DQ坐标系交轴Q中的分量给定值Iq*。其内部结构如图3所示,其中输入信号有两个,一个是转矩给定量T * e,另一个是转子磁通Phir。f(u)是数学函数,用于计算定子绕组电流的Q轴分量给定值Iq*。函数中包含电动机磁极对数P,折算后的转子电感Lr,定子、转子间的互感Lm。
3.3.2 DQ-ABC子模块
DQ-ABC模块是坐标变换模块,它将DQ坐标系中的定子电流分量旋转变换后,得到ABC坐标系下电机定子绕组的给定电流值Iabc。
3.3.3 Teta Caculation子模块
Teta Calculation模块是角度计算模块,它可以计算出旋转磁场与旋转坐标的空间电角度θ,即M轴的位置。其内部结构如图4所示。
在图4中,f(u)是转差频率计算函数,它根据定子绕组电流的Q轴分量Iq及转子磁通Phir计算得出电动机的转差率,其表达式为:
式中:Lm为转子和定子之间的互感;T2为电枢回路的时间常数。
3.3.4 ABC-DQ子模块
ABC-DQ模块是坐标变换模块,它的作用是根据电角度θ将电动机实际三相定子电流Iabc变换得到其在DQ坐标系下的两个分量Id和Iq。
3.3.5 Flux Calculation子模块
Flux Calculation模塊是磁通计算模块,它的作用是根据定子电流励磁分量Id来计算出电机转子的磁通Phir。Phir计算公式如下:
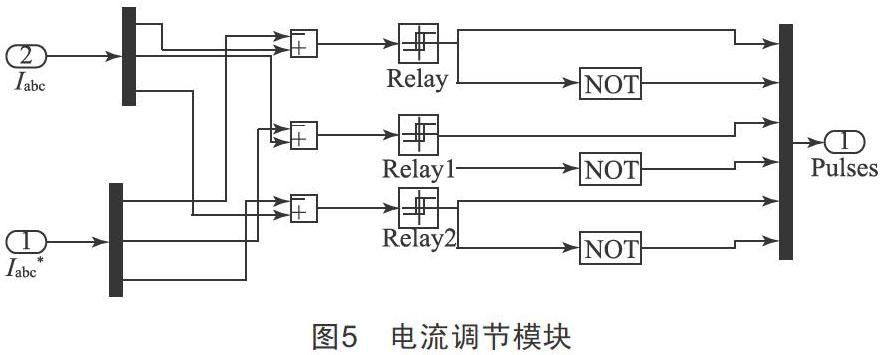
3.3.6 Current Regulator子模块
Current Regulator是电流调节模块,如图5所示。该仿真模型采用电流滞环控制原理进行调节,使实际输出电流的变化跟随给定值变化。
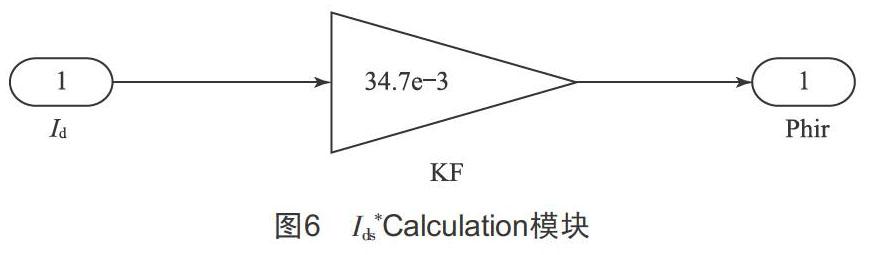
3.3.7 Ids* Calculation 子模块
此模块可以根据转子磁通计算出定子的电流励磁分量Ids*,Ids* Calculation模块如图6所示。
3.3.8 ASR子模块
ASR为速度调节子模块,它将电机实际反馈速度与参考转速的差值作为输入信号,经过PI控制器调节后向电动机发出转矩指令,其模型如图7所示。其中,比例系数Kp设为13,积分系数Ki设为26,输出转矩限幅设为300 Nm。
4 仿真结果与分析
现在利用图2所示的仿真模型,对转差型三相异步电动机矢量控制系统进行仿真研究,系统仿真结果如图8所示。在电动机观测模块Demux中确定定子三相电流、电磁转矩、转子转速为被测对象,用电压观测模块Vab对电机定子三相绕组线电压进行监测。
三相异步电动机仿真模型中涉及的主要参数设定如下:额定功率3.7 kW,额定频率50 Hz,线电压380 V,定子漏感0.8 mH,转子内阻0.228 Ω,定子内阻0.087 Ω,定/转子互感34.7 mH,转子漏感0.8 mH,极对数为2。
在SIMULINK中设定仿真时长为10 s,步长模式选Variable-step(可变步长),选择ode23tb仿真算法。电流调节器选用滞环型PWM控制器,滞环宽度设定为20。
从图8(b)中可以发现,电动机开始启动的瞬间,电动机定子绕组的电流快速上升,其峰值已经达到400 A左右。在恒转矩启动阶段,定子绕组励磁电流达到最大饱和值180 A,整个恒转矩起动过程大约在3.8 s完成。在恒转矩时段,电动机输出转矩基本维持在最大值3 00 Nm左右,该极限值是通过速度控制器ASR的参数表提前设定好的。经过大约4 s后电动机转速会上升到最大值,5 s左右恢复到正常状态,而后转速变化很小,基本保持在80 r/min的稳定速度运行。
5 结语
本文对交流异步电动机的动态电磁关系进行了详细分析,给出了转子坐标系下异步电动机的传递函数,并运用MATLAB/SIMULINK软件对转差率型矢量控制系统进行了仿真分析。仿真结果表明,该系统启动迅速,恢复时间较短,抗干扰性能突出,运行稳定可靠。由此可见,采用矢量控制方式的交流异步电动机控制系统具有良好的动态和静态性能。
[参考文献]
[1] 蒯松岩,衡凤平,崔鑫,等.基于Matlab的“运动控制系统”课程教学改革[J].电气电子教学学报,2016,38(1):29-31.
[2] 孙伟,于泳,王高林,等.基于矢量控制的异步电机预测电流控制算法[J].中国电机工程学报,2014,34(21):3448-3455.
[3] 杨馥华.异步电动机变频调速系统仿真设计平台的研究[J].北京:华北电力大学,2012.
收稿日期:2020-07-24
作者简介:林海翔(1984—)男,江苏宝应人,高校讲师,研究方向:自动化、电机与控制。
